【研究意义】在理论研究和工程实践中,许多问题的解决需要根据观测数据来恢复或重构物理介质的结构信息,通常称这类问题为逆问题.逆问题分为线性逆问题和非线性逆问题,其中线性逆问题广泛出现在地球物理学、图像处理、地下水文学、全球海洋模拟、肿瘤检测、非破坏性检测等领域中[1].【前人研究进展】对于线性逆问题的研究,已有不少数值解法,文献[2]提出迭代Tikhonov正则化方法求解该问题,取得了较好的数值效果.文献[3]提出了Levenberg-Marquardt方法求解该问题,且在数值试验中,用偏差原则作为停止准则,但该方法所需CPU时间较长.文献[4]提出并讨论了一类NCPs逆问题.【本研究切入点】谱共轭梯度法是一类非常重要的优化方法,他是将谱梯度法和共轭梯度法的思想相结合的一种方法,具有迭代简单、易于编程以及存储要求低等优点,所以一般适用于求解大规模无约束优化问题.近年来,文献[5-7]用谱共轭梯度法求解线性和非线性优化问题,得到很好的数值效果.因此,本文希望把谱共轭梯度法应用到线性逆问题中.【拟解决的关键问题】针对线性逆问题,提出一个新的谱共轭梯度法,在理论上证明新提共轭梯度法的下降性和全局收敛性,并把该方法应用到卷积方程反演和图像处理的反演中.
1 新的谱共轭梯度法在许多科学研究和工程应用中,很多问题可以转化为下面形式的算子方程
| $Hx=u.$ | (1) |
我们研究的问题是已知H和u反解x,这里H表示线性算子,u为实验测得的数据,因而不可避免地带有一定的噪声[1],即有
| ${{u}_{e}}=u+\eta ,$ | (2) |
这里,η表示与u维数相同的噪声。即问题(1)转化为求解
| $Hx={{u}_{e}}.$ | (3) |
为了便于求解,将问题(3)等价转化为求解下面的最小二乘问题:
| $min~f\left( x \right)=\|Hx-{{u}_{e}}{{\|}^{2}}.$ | (4) |
由于H是一个条件数很大的病态矩阵,所以问题(3)是一个不适定问题,因此没有唯一解.为了克服问题(3)的不适定性,本文在式(4)的基础上通过增加一个Tikhonov正则项‖x‖2,将不适定问题转化为适定问题,即求解下面的无约束优化问题:
| $min~f\left( x \right)=\|Hx-u{{\|}^{2}}+\alpha \|x{{\|}^{2}},$ | (5) |
其中,α为正则化参数,而且该参数的选取对问题的求解发挥重要作用.
对于无约束优化问题:
| $min~\{f\left( x \right)|x\in {{R}^{n}}\},$ | (6) |
其中f(x)为式(5)的目标函数.共轭梯度法是求解问题(5)的有效方法[8-10],其标准迭代形式为
| ${{x}_{k+1}}={{x}_{k}}+{{\alpha }_{k}}{{d}_{k}},$ | (7) |
其中αk是Wolfe搜索产生的步长,dk为搜索方向.dk定义为
| ${{d}_{k}}=\left\{ \begin{matrix} -{{g}_{k}},k=1, \\ -{{g}_{k}}+{{\beta }_{k}}{{d}_{k-1}},k\ge 2, \\ \end{matrix} \right.$ | (8) |
其中gk=Δf(xk),βk为方向调控参数.不同的βk对应不同的共轭梯度法,其中著名的βk 计算公式[11-12]有
| $\beta _{k}^{~CD}=-\frac{g_{k}^{T}{{g}_{k}}}{d_{k-1}^{T}{{g}_{k-1}}},\beta _{k}^{LS}=-\frac{g_{k}^{T}({{g}_{k}}-{{g}_{k-1}})}{g_{k-1}^{T}{{d}_{k-1}}}.$ | (9) |
上述由参数βk构成的方法分别称为CD方法和LS方法.
Birgin等[13]结合谱梯度的思想,提出了下面形式的谱共轭梯度法:
| ${{d}_{k}}=\left\{ \begin{matrix} -{{g}_{k}},k=1, \\ -{{\theta }_{k}}{{g}_{k}}+{{\beta }_{k}}{{d}_{k-1}},k>1, \\ \end{matrix} \right.$ | (10) |
并取
| ${{\beta }_{k}}=\frac{{{\left( {{\theta }_{k}}{{y}_{k-1}}-{{s}_{k-1}} \right)}^{T}}{{g}_{k}}}{d_{k-1}^{T}{{y}_{k-1}},}$ | (11) |
| ${{\theta }_{k}}=\frac{s_{k-1}^{T}{{s}_{k-1}}}{s_{k-1}^{T}{{y}_{k-1}}},$ | (12) |
其中yk-1=gk-gk-1,sk-1=xk-xk-1.基于迭代格(10),本文给出新的βk和θk(文献[14])分别为
| ${{\beta }_{k}}=\frac{\|{{g}_{k}}{{\|}^{2}}+1}{d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})},$ | (13) |
| $\frac{\left( 1+\frac{1}{{{\left\| {{g}_{k}} \right\|}^{2}}} \right)g_{k}^{T}{{d}_{k-1}}-\left( 1+\frac{2}{{{\left\| {{g}_{k}} \right\|}^{2}}} \right)g_{k-1}^{T}{{d}_{k-1}}}{d_{k-1}^{T}\left( {{g}_{k}}-{{g}_{k-1}} \right)}.$ | (14) |
称式(10),(13),(14)为新的谱共轭梯度法(SCG).以下结合Wolfe线搜索建立新的谱共轭梯度算法,并分析算法的收敛性质.
算法1
步骤1 给定初值x1∈Rn,0<δ<1/2<σ<1,d1:=-g1,ε≥0.如果‖g1‖≤ε,则停止迭代.
步骤2 由Wolfe线搜索准则计算步长αk,即αk满足:
| $f\left( {{x}_{k}}+{{\alpha }_{k}}{{d}_{k}} \right)-{{f}_{k}}\le \delta {{\alpha }_{k}}g_{k}^{T}{{d}_{k}},$ | (15) |
| $g{{\left( {{x}_{k}}+{{\alpha }_{k}}{{d}_{k}} \right)}^{T}}{{d}_{k}}\ge \sigma g_{k}^{T}{{d}_{k}}.$ | (16) |
步骤3 计算xk+1=xk+αkdk.若‖gk+1‖≤ε,则停止迭代.
步骤4 由式(13)计算βk+1,由式(14)计算θk+1,由dk+1=-θk+1gk+1+βk+1dk计算dk+1.
步骤5 k:=k+1,转步骤2.
以下均假设‖gk‖≠0,否则算法因已找到稳定点而停止.
引理1 设{gk}和{dk}为算法1生成的序列,则
| $g_{k}^{T}{{d}_{k}}<0,\forall k\ge 1.$ | (17) |
证明 用数学归纳法证明.当k=1时,g1Td1=g1T(-g1)=-‖g1‖2<0.现假设对于k-1的情形有gTk-1dk-1<0成立,由式(16)可得
| $d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})\ge \left( \sigma -1 \right)g_{k-1}^{T}{{d}_{k-1}}>0.$ | (18) |
则对于k的情形就有
| $\begin{align} & g_{k}^{T}{{d}_{k}}=g_{k}^{T}\left( -{{\theta }_{k}}{{g}_{k}}+{{\beta }_{k}}{{d}_{k-1}} \right)= \\ & \frac{-(1+\|{{g}_{k}}{{\|}^{2}})g_{k}^{T}{{d}_{k-1}}+(\|{{g}_{k}}{{\|}^{2}}+2)g_{k-1}^{T}{{d}_{k-1}}}{d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})}+ \\ & \frac{(\|{{g}_{k}}{{\|}^{2}}+1)g_{k}^{T}{{d}_{k-1}}}{d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})}\text{ }=\frac{(\|{{g}_{k}}{{\|}^{2}}+2)g_{k-1}^{T}{{d}_{k-1}}}{d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})}<0. \\ \end{align}$ | (19) |
从而由数学归纳法知引理1成立.
引理1 说明算法1产生的搜索方向是下降方向.
引理2 如果步长因子αk满足Wolfe线搜索条件,则有
| $0<{{\beta }_{k}}<\frac{g_{k}^{T}{{d}_{k}}}{g_{k-1}^{T}{{d}_{k-1}}}.$ | (20) |
证明 由式(13)可得
| ${{\beta }_{k}}=\frac{\|{{g}_{k}}{{\|}^{2}}+1}{d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})}>0.$ | (21) |
对式(19)两边同时除以gk-1Tdk-1,可得
| $\frac{g_{k}^{T}{{d}_{k}}}{g_{k-1}^{T}{{d}_{k-1}}}=\frac{\|{{g}_{k}}{{\|}^{2}}+2}{d_{k-1}^{T}({{g}_{k}}-{{g}_{k-1}})}>$ | (22) |
| $\begin{align} & \frac{\|{{g}_{k}}{{\|}^{2}}+1}{d_{k-1}^{T}\left( {{g}_{k}}-{{g}_{k-1}} \right)}={{\beta }_{k}}< \\ & \frac{g_{k}^{T}{{d}_{k}}}{g_{k-1}^{T}{{d}_{k-1}}}. \\ \end{align}$ | (23) |
所以,引理2得证.
2 算法的全局收敛性(H1)目标函数f(x)在其水平集Ω={x∈Rn|f(x)≤f(x1)}上有界.
(H2)设f(x)的梯度g(x)在Ω上Lipschitz连续,即存在L>0,使
| $\|g\left( y \right)-g\left( x \right)\|\le L\|y-x\|,\forall x,y\in \Omega .$ | (24) |
引理3 假设(H1),(H2)成立,{gk}和{dk}为算法 1 生成的序列,则
| $\sum\limits_{k\ge 1}{\frac{{{(g_{k}^{T}{{d}_{k}})}^{2}}}{\|{{d}_{k}}{{\|}^{2}}}}<+\infty .$ | (25) |
证明 由式(7)和式(16)及假设(H2),可得
| $L{{\alpha }_{k}}\|{{d}_{k}}{{\|}^{2}}\ge d_{k}^{T}({{g}_{k+1}}-{{g}_{k}})\ge \left( \sigma -1 \right)g_{k}^{T}{{d}_{k}},$ | (26) |
从而得到
| ${{\alpha }_{k}}\ge \frac{\left( \sigma -1 \right)}{L}\frac{g_{k}^{T}{{d}_{k}}}{\|{{d}_{k}}{{\|}^{2}}}.$ | (27) |
由Wolfe搜索准则和dk的下降性及假设(H1)知,{fk}为单调递减的收敛数列,结合式(27)可得
| ${{f}_{k}}-{{f}_{k+1}}\ge -\delta {{\alpha }_{k}}g_{k}^{T}{{d}_{k}}\ge \frac{\delta \left( 1-\sigma \right)}{L}\frac{{{(g_{k}^{T}{{d}_{k}})}^{2}}}{\|{{d}_{k}}{{\|}^{2}}}.$ | (28) |
对式(28)左右两端分别从k=1,2,…求和,再利用{fk}的收敛性,可得式(25)成立,则引理3得证.
定理1 假设(H1),(H2)成立,{gk}为算法1生成的序列,则
| $\underset{k\to \infty }{\mathop{lim}}\,~inf~\|{{g}_{k}}\|=0.$ | (29) |
证明 若定理1不成立,则必存在常数r>0,使得对任意的k≥1,有
| $\|{{g}_{k}}\|\ge r.$ | (30) |
式(10)移项,得dk+θkgk=βkdk-1,等式两端取模平方,移项并利用式(20),可得
| $\begin{align} & \|{{d}_{k}}{{\|}^{2}}={{\left( {{\beta }_{k}} \right)}^{2}}\|{{d}_{k-1}}{{\|}^{2}}-2{{\theta }_{k}}g_{k}^{T}{{d}_{k}}- \\ & \theta _{k}^{2}\|{{g}_{k}}{{\|}^{2}}~<\frac{{{(g_{k}^{T}{{d}_{k}})}^{2}}}{{{(g_{k-1}^{T}{{d}_{k-1}})}^{2}}}\|{{d}_{k-1}}{{\|}^{2}}-2{{\theta }_{k}}g_{k}^{T}{{d}_{k}}- \\ & \theta _{k}^{2}\|{{g}_{k}}{{\|}^{2}}. \\ \end{align}$ | (31) |
式(31)两端同时除以(gkTdk)2,可得
| $\begin{align} & \frac{\|{{d}_{k}}{{\|}^{2}}}{{{\left( g_{k}^{T}{{d}_{k}} \right)}^{2}}}<\frac{\|{{d}_{k-1}}{{\|}^{2}}}{{{\left( g_{k-1}^{T}{{d}_{k-1}} \right)}^{2}}}-\frac{2{{\theta }_{k}}}{g_{k}^{T}{{d}_{k}}}-\frac{\theta _{k}^{2}\|{{g}_{k}}{{\|}^{2}}}{{{\left( g_{k}^{T}{{d}_{k}} \right)}^{2}}}~= \\ & \frac{\|{{d}_{k-1}}{{\|}^{2}}}{{{\left( g_{k-1}^{T}{{d}_{k-1}} \right)}^{2}}}+\frac{1}{\|{{g}_{k}}{{\|}^{2}}}-{{\left( \frac{1}{\|{{g}_{k}}\|}+\frac{{{\theta }_{k}}\|{{g}_{k}}\|}{\left( g_{k}^{T}{{d}_{k}} \right)} \right)}^{2}}< \\ & \frac{\|{{d}_{k-1}}{{\|}^{2}}}{{{(g_{k-1}^{T}{{d}_{k-1}})}^{2}}}+\frac{1}{\|{{g}_{k}}{{\|}^{2}}}. \\ \end{align}$ | (32) |
由式(32)的递推,并利用d1=-g1,可得
| $\begin{align} & \frac{\|{{d}_{k}}{{\|}^{2}}}{{{\left( g_{k}^{T}{{d}_{k}} \right)}^{2}}}<\frac{\|{{d}_{1}}{{\|}^{2}}}{\|{{g}_{1}}{{d}_{1}}{{\|}^{2}}}+ \\ & \sum\limits_{i=2}^{k}{\frac{1}{\|{{g}_{i}}{{\|}^{2}}}}=\sum\limits_{i=1}^{k}{\frac{1}{\|{{g}_{i}}{{\|}^{2}}}}. \\ \end{align}$ | (33) |
结合式(30),可得
| $\frac{{{(g_{k}^{T}{{d}_{k}})}^{2}}}{\|{{d}_{k}}{{\|}^{2}}}>\frac{{{r}^{2}}}{k}.$ | (34) |
对式(34)两端分别求和可得
| $\sum\limits_{k\ge 1}{\frac{{{(g_{k}^{T}{{d}_{k}})}^{2}}}{\|{{d}_{k}}{{\|}^{2}}}}>{{r}^{2}}\sum\limits_{k\ge 1}{\frac{1}{k}}=+\infty ,$ | (35) |
显然,式(35)与式(25)矛盾,所以定理1成立.
3 数值实验算法测试的环境为Matlab 2013a,Windows 7操作系统,Intel(R)Core(TM) i3-2370M CPU @6.40 GHz.用Matlab的rand函数在真实解上添加一定水平的噪声.参数δ=0.025,σ=0.9,α=0.014.为了评价不同方法的求解效果,引入真实解和数值解的均方根误差(RMSE)的指标[17-18]来衡量:
| $RMSE=\frac{\|x-{{x}_{k}}{{\|}_{2}}}{\|x{{\|}_{2}}},$ | (36) |
其中,x和xk分别是真实解和数值解,显然RMSE越小,数值解对应的算法越好.停止准则是
| $\|{{g}_{k}}\|\le {{10}^{-5}}.$ | (37) |
例1 卷积方程的反演
考察在位势理论中有重要应用的卷积方程[1]:
| $\begin{align} & -\frac{1}{2\pi }\int_{0}^{2\pi }{(1-ln(4si{{n}^{2}}\left( t-t\prime \right)/2))x\left( t\prime \right)d\left( t\prime \right)} \\ & =u\left( t \right),0\le t\le 2\pi , \\ \end{align}$ | (38) |
其中u(t)与位势方程边界条件有关,弱奇异性核H(t,t′)=1-ln(4sin2(t-t′)/2).现将式(38)记为算子形式:
| $\int_{0}^{2\pi }{H\left( t,t\prime \right)x\left( t\prime \right)dt\prime =u\left( t \right),0\le t\le 2\pi }.$ | (39) |
用配置法离散式(39)得到离散的算子方程H(t)x(t)=u(t).
假设观测数据是在真实数据上添加一定噪声水平的高斯白噪声[19],则有
| ${{u}_{e}}=u+e*rand(size\left( u \right)),$ | (40) |
其中,e表示噪声水平,rand(·)表示维数与u相同的高斯白噪声,即有
| $H\left( t \right)x\left( t \right)={{u}_{e}}\left( t \right).$ | (41) |
问题(41)等价于求解下列无约束优化问题:
| $min~f\left( x\left( t \right) \right)=\|H\left( t \right)x\left( t \right)-{{u}_{e}}\left( t \right){{\|}^{2}}.$ | (42) |
为了克服问题(41)的不适定性,引入Tikhonov正则项,即该问题转化为求解下述问题:
| $\begin{align} & min~f\left( x\left( t \right) \right)=\|H\left( t \right)x\left( t \right)-{{u}_{e}}\left( t \right){{\|}^{2}} \\ & +\gamma \|x\left( t \right){{\|}^{2}}, \\ \end{align}$ | (43) |
这里,α表示正则化参数.
选择核函数H(t)和真实解xtrue(x):
| ${{x}_{true}}=exp~(3sin~t),$ | (44) |
| $H\left( t \right)=\frac{1}{0.05\sqrt{\pi }}exp~(-\frac{{{\left( t-1/200 \right)}^{2}}}{{{0.05}^{2}}}).$ | (45) |
在实验中,离散点设置为256个单位,即矩阵H(t)∈R256×256,真实解xture(w,t)∈R256,观测数据ue(t)的噪声水平设置为e=0.01,现用观测数据ue(t)来反演x(t).
为了更公平的测试算法的速度,每个实验重复做10次,结果的平均值见表 1.从表 1可以看出本文提出的谱共轭梯度法(SCG)的REMS值相对较小,且求解过程所需的迭代次数和CPU时间也是最小的,说明SCG方法所需更少的计算代价.
| 表 1 4种算法的数值结果 Table 1 Numerical results of four algorithms |
从图 1~4可以看出SCG方法具有一定的优势.从图 5的效果图也可以得出SCG方法是有效的.
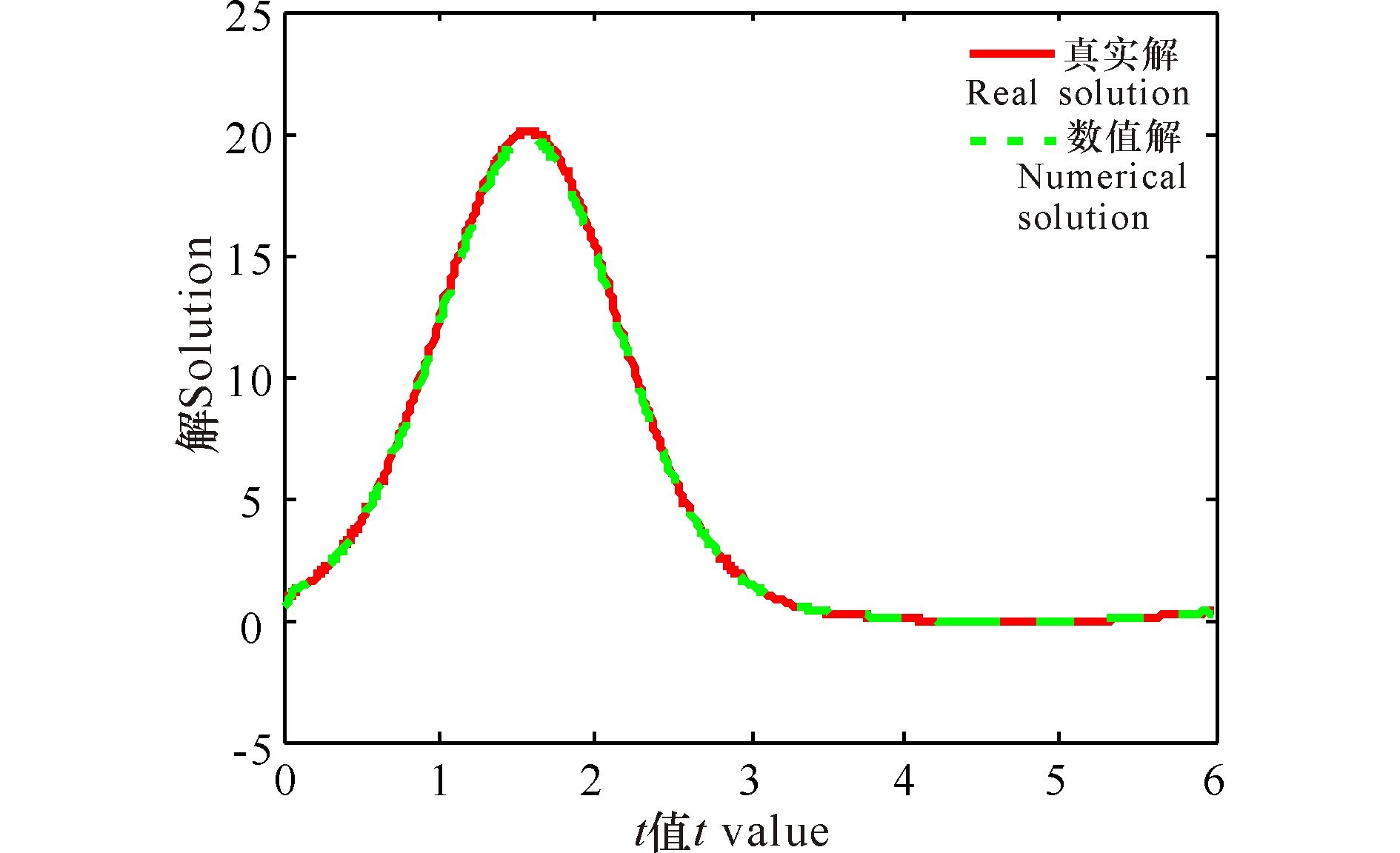
|
图 1 Landweber法求解例1的数值结果 Fig.1 Numerical results of sample 1 obtained from Landweber method |
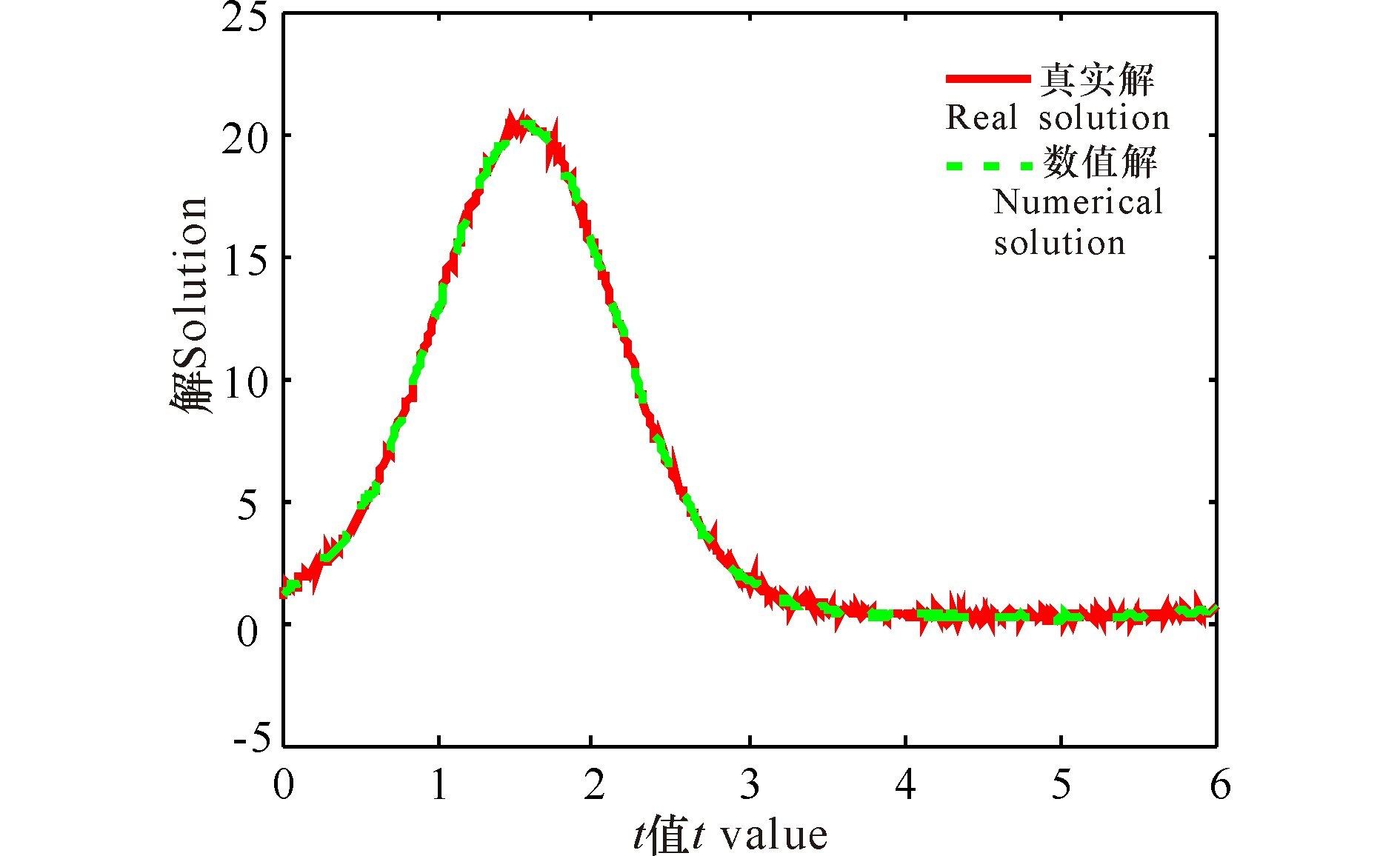
|
图 2 TSVD法求解例1的数值结果 Fig.2 Numerical results of sample 1 obtained from TSVD method |

|
图 3 TV法求解例1的数值结果 Fig.3 Numerical results of sample 1 obtained from TV method |
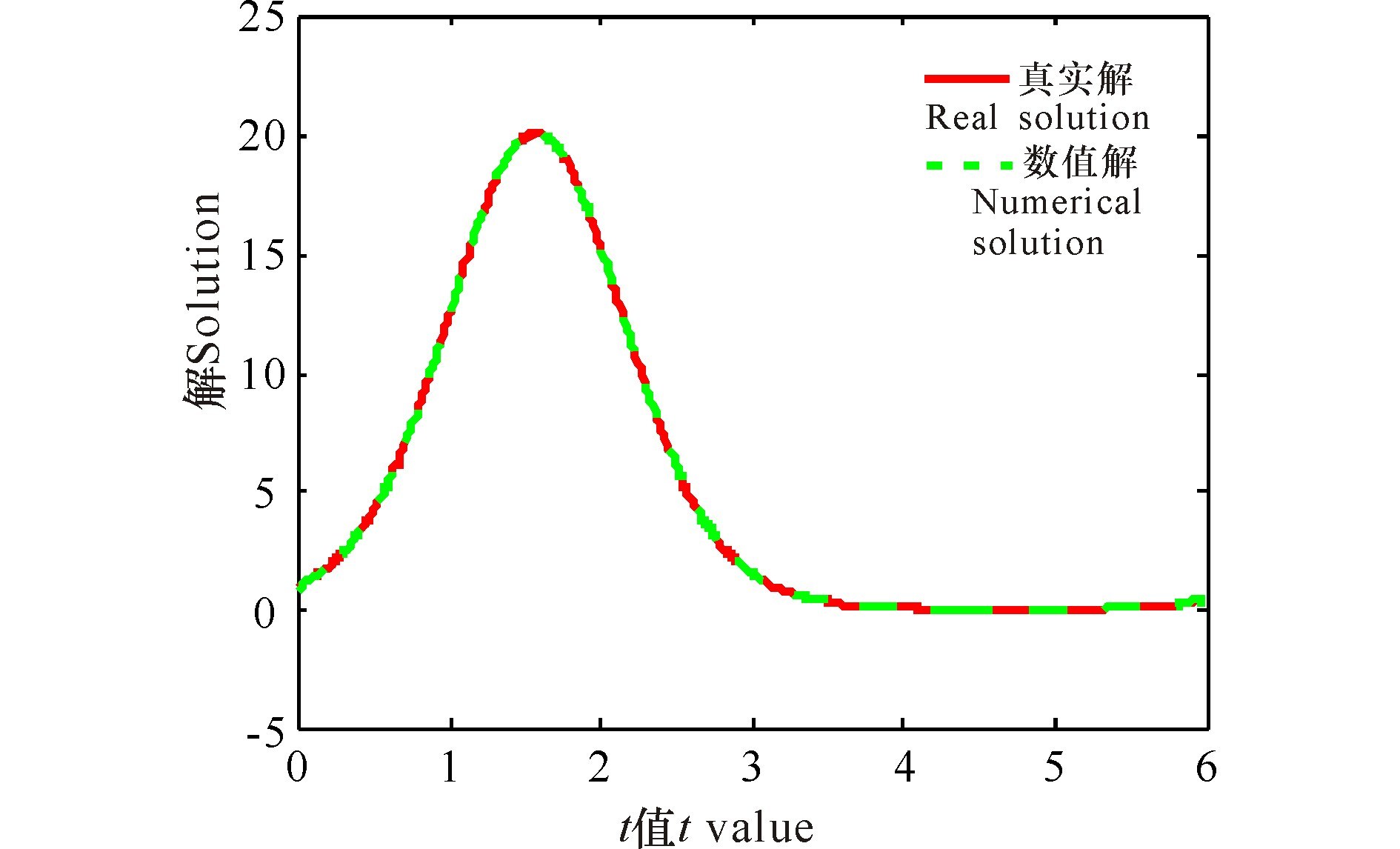
|
图 4 SCG法求解例1的数值结果 Fig.4 Numerical results of sample 1 obtained from SCG method |
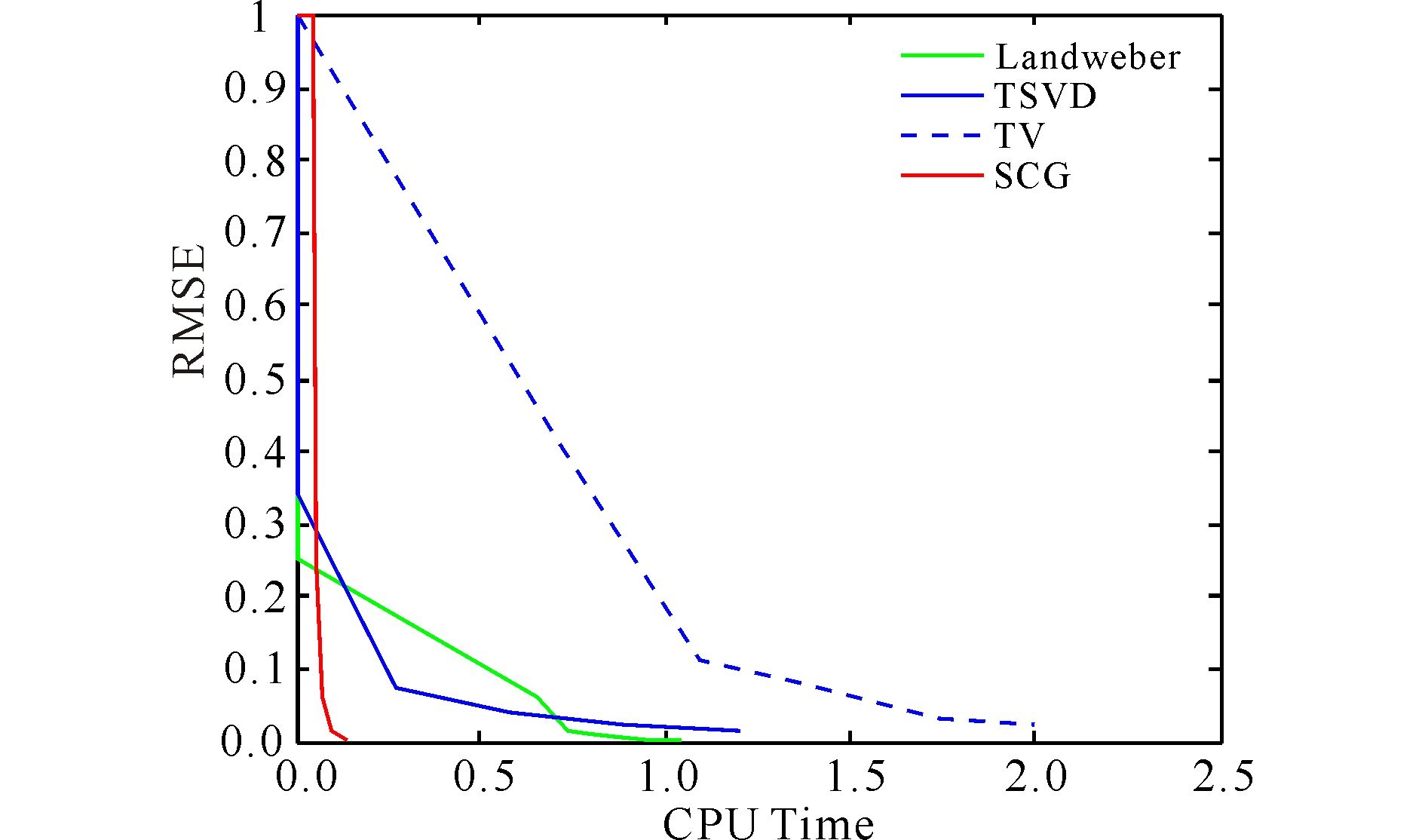
|
图 5 例1效果图 Fig.5 Effects diagram for sample 1 |
例2 图像处理的反演问题
考察简单的一维情形图像识别问题,如方程:
| $\int_{a}^{b}{h\left( t-t\prime \right)x\left( t\prime \right)=u\left( t \right)},$ | (46) |
其中x(t′)代表光源强度,u(t)代表观测的图像,通常是一个模糊核的连续图像;h(t-t′)表示成像的过程,通常是一个点扩展函数(PSF).问题给定光源函数x(t′)和点扩展函数h(t-t′)来求观测图像u(t).与此相关的反问题:给定点扩展函数h(t-t′)和观测图像u(t)来确定光源强度x(t′).
由有限差分法离散式(39)得到离散的算子方程
| $H\left( t \right)x\left( t \right)=u\left( t \right),$ | (47) |
假设观测数据为在真实数据上添加imnoise函数产生的高斯噪声,则有
| ${{u}_{e}}=u+e*imnoise(size\left( u \right)),$ | (48) |
其中,e表示噪声水平,imnoise(·)表示维数与u相同的高斯噪声,即有
| $H\left( t \right)x\left( t \right)={{u}_{e}}\left( t \right).$ | (49) |
问题(49)等价于求解下列无约束优化问题:
| $min~f\left( x\left( t \right) \right)=\|H\left( t \right)x\left( t \right)-{{u}_{e}}\left( t \right){{\|}^{2}}.$ | (50) |
为了克服问题(49)的不适定性,引入Tikhonov正则项,即转该问题化为求解下述问题:
| $\begin{align} & min~f\left( x\left( t \right) \right)=\|H\left( t \right)x\left( t \right)-{{u}_{e}}\left( t \right){{\|}^{2}} \\ & +\gamma \|x\left( t \right){{\|}^{2}}, \\ \end{align}$ | (51) |
这里,γ表示正则化参数.
选择核函数H(t)和真实解xtrue(x):
| ${{x}_{true}}=si{{n}^{4}}(2\pi t),$ | (52) |
| $H\left( t \right)=\frac{1}{1+100{{\left( t-0.5 \right)}^{2}}~}.$ | (53) |
在实验中,离散点设置为512个单位,即矩阵H(t)∈R512×512,真实解xture(w,t)∈R512,观测数据ue(t)的噪声水平设置为e=0.02,现用观测数据ue(t)来反演x(t).
为了更公平的测试算法的速度,每个实验重复做10次(表 2).从表 2可以看出,SCG方法的RMSE值是0.012,在4个算法中相对较小,而且求解过程所需的迭代次数和CPU时间都相对较小,因此SCG方法所需求解成本相对较低.
| 表 2 4种算法的数值结果 Table 2 Numerical results of four algorithms |
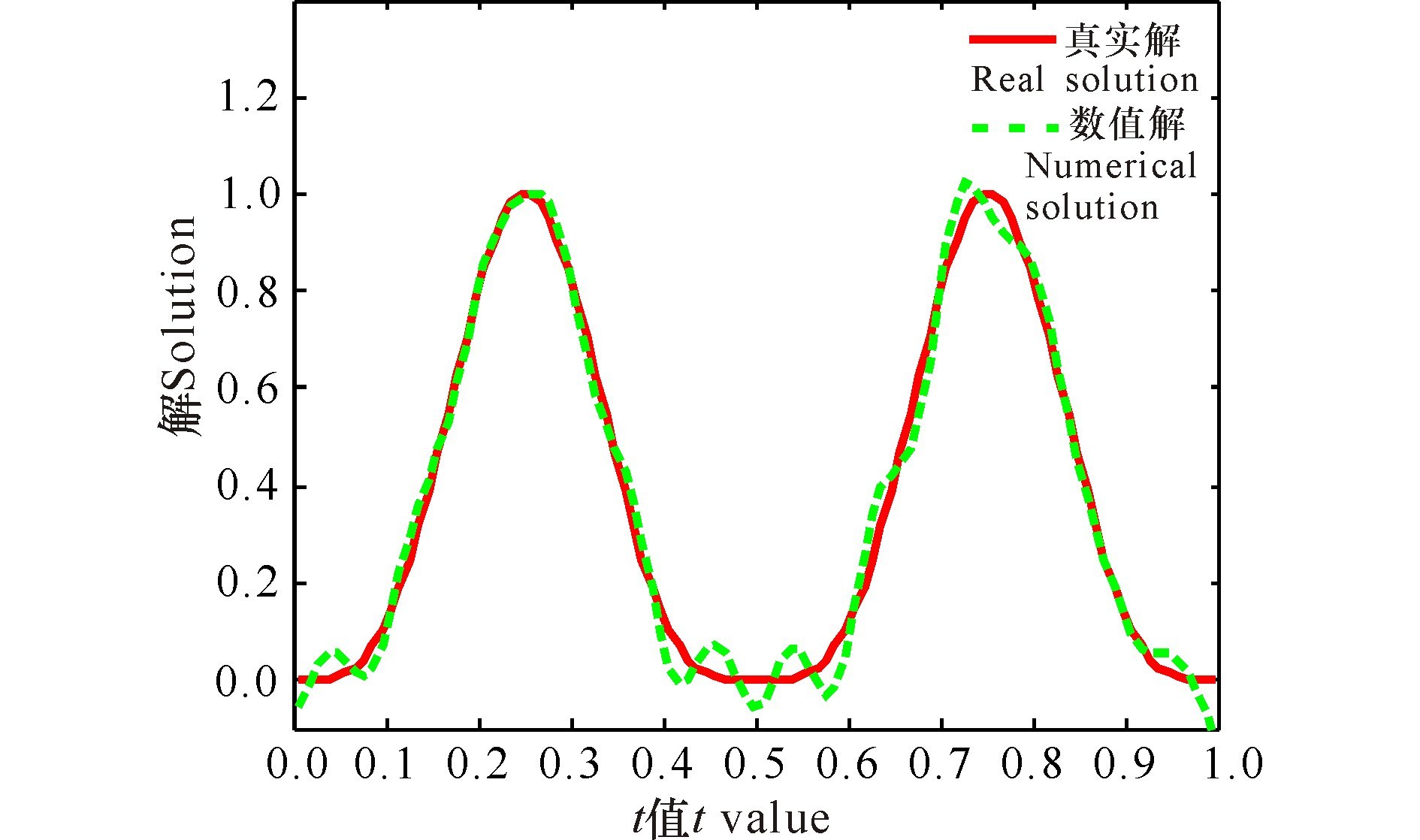
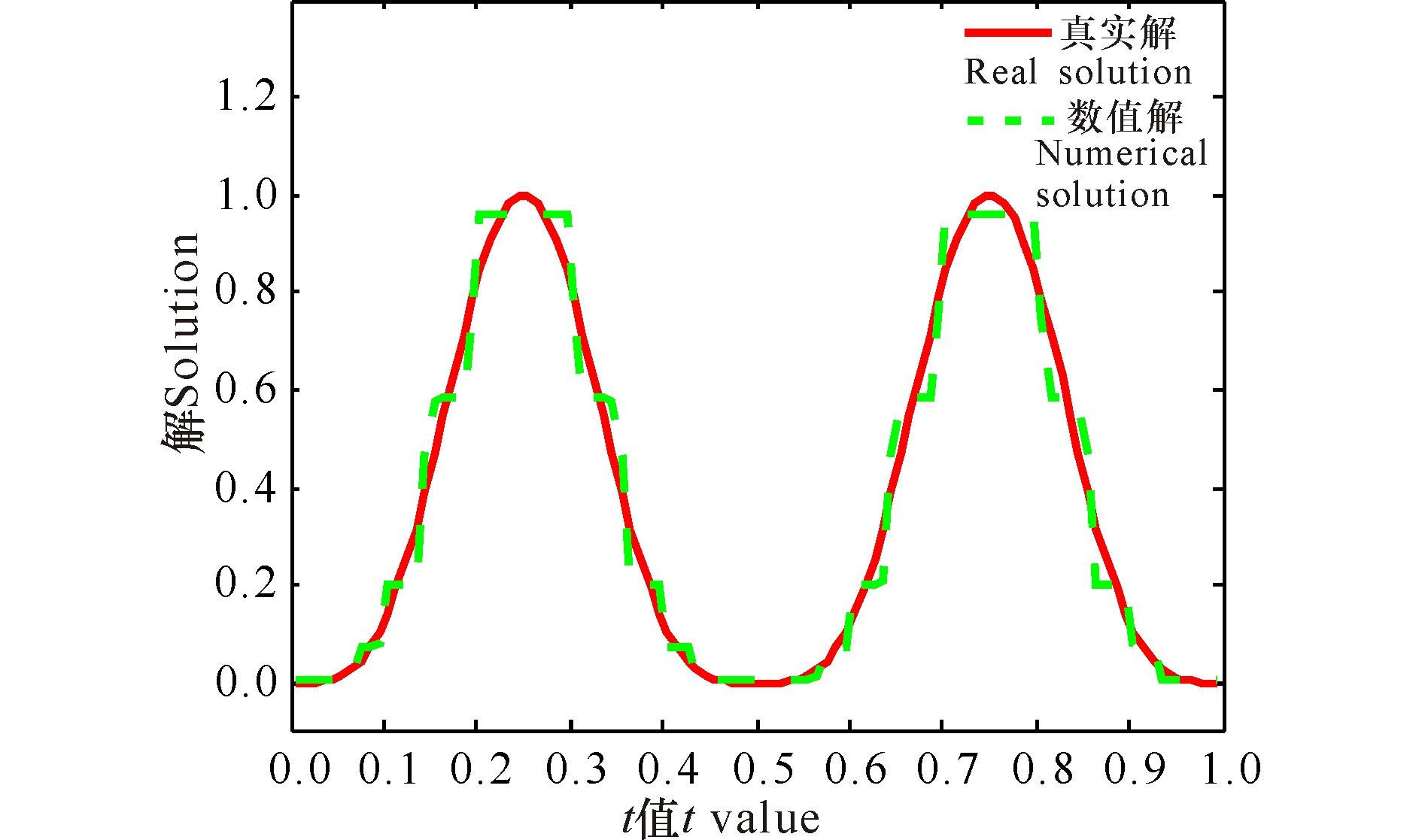
从图 6~9可以看出SCG方法的数值解比较理想的逼近真实解.从图 10的效果图也可以得出,SCG方法比其他3种算法更有效.

|
图 6 Landweber法求解例2的数值结果 Fig.6 Numerical results of sample 2 obtained from Landweber method |
|
图 7 TSVD法求解例2的数值结果 Fig.7 Numerical results of sample 2 obtained from TSVD method |
|
图 8 TV法求解例2的数值结果 Fig.8 Numerical results of sample 2 obtained from TV method |

|
图 9 SCG法求解例2的数值结果 Fig.9 Numerical results of sample 2 obtained from SCG method |

|
图 10 例2效果图 Fig.10 Effects diagram for sample 2 |
本文提出一个求解线性逆问题的新谱共轭梯度法,证明了该算法的全局收敛性,并利用该方法对卷积方程的反演问题和图像处理的反演问题进行数值实验,发现该方法比Landweber,TSVD和TV方法更有效.
| [1] |
肖庭延, 于慎根, 王彦飞. 反问题的数值解法[M]. 北京: 科学出版社, 2003: 166-174. XIAO T Y, YU S G, WANG Y F. Numerical Solution of Inverse Problem[M]. Beijing: Science Press, 2003: 166-174. |
| [2] |
LIU W, WU C S. A predictor-corrector iterated Tik-honov regularization for linear ill-posed inverse problems[J]. Applied Mathematics and Computation, 2013, 221: 802-818. DOI:10.1016/j.amc.2013.06.080 |
| [3] |
JIN Q N. On a regularized Levenberg-Marquardt method for solving nonlinear inverse problems[J]. Numerische Mathematik, 2010, 115(2): 229-259. DOI:10.1007/s00211-009-0275-x |
| [4] |
ZHANG J Z, JIAN J B, TANG C M. Inverse problems and solution methods for a class of nonlinear complementarity problems[J]. Computational Optimization and Applications, 2011, 49(2): 271-297. DOI:10.1007/s10589-009-9294-x |
| [5] |
江羡珍, 马国栋, 简金宝. Wolfe线搜索下一个新的全局收敛共轭梯度法[J]. 工程数学学报, 2011, 28(6): 779-786. JIANG X Z, MA G D, JIAN J B. A new globally convergent conjugate gradient method with Wolfe line search[J]. Chinese Journal of Engineering Mathematics, 2011, 28(6): 779-786. |
| [6] |
江羡珍, 韩麟, 简金宝. Wolfe线搜索下一个全局收敛的混合共轭梯度法[J]. 计算数学, 2012, 34(1): 103-112. JIANG X Z, HAN L, JIAN J B. A globally convergent mixed conjugate gradient method with Wolfe line search[J]. Mathematica Numerica Sinica, 2012, 34(1): 103-112. |
| [7] |
JIAN J B, HAN L, JIANG X Z. A hybrid conjugate gradient method with descent property for unconstrained optimization[J]. Applied Mathematical Modelling, 2015, 39(3/4): 1281-1290. |
| [8] |
简金宝, 尹江华, 江羡珍. 一个充分下降的有效共轭梯度法[J]. 计算数学, 2015, 37(4): 415-424. JIAN J B, YIN J H, JIANG X Z. An efficient conjugate gradient method with sufficient descent property[J]. Mathematica Numerica Sinica, 2015, 37(4): 415-424. |
| [9] |
韩麟, 简金宝, 江羡珍. Armijo线搜索下一个杂交共轭梯度法及其强收敛性[J]. 玉林师范学院学报:自然科学, 2013, 34(2): 17-21. HAN L, JIAN J B, JIANG X Z. A mixed conjugate gradient method with Armijo linear search and its strong convergence[J]. Journal of Yulin Normal University:Natural Science, 2013, 34(2): 17-21. |
| [10] |
JIANG X Z, JIAN J B. Two modified nonlinear conjugate gradient methods with disturbance factors for unconstrained optimization[J]. Nonlinear Dynamics, 2014, 77(1/2): 387-397. |
| [11] |
POLAK E, RIBIRE G. Note sur la convergence de méthodes de directions conjuguées[J]. Revue Franaise D'informatique et de Recherche Opérationnelle, 1969, 16: 35-43. |
| [12] |
POLYAK B T. The conjugate gradient method in extreme problems[J]. Ussr Computational Mathematics and Mathematical Physics, 1969, 9(4): 94-112. DOI:10.1016/0041-5553(69)90035-4 |
| [13] |
BIRGIN E G, MARTNEZ J M. A spectral conjugate gradient method for unconstrained optimization[J]. Applied Mathematics and Optimization, 2001, 43(2): 117-128. DOI:10.1007/s00245-001-0003-0 |
| [14] |
JIANG X Z, JIAN J B. A sufficient descent Dai-Yuan type nonlinear conjugate gradient method for unconstrained optimization problems[J]. Nonlinear Dynamics, 2013, 72(1/2): 101-112. |
| [15] |
江羡珍, 简金宝, 马国栋. 具有充分下降性的两个共轭梯度法[J]. 数学学报, 2014, 57(2): 365-372. JIANG X Z, JIAN J B, MA G D. Two conjugate gradient methods with sufficient descent property[J]. Acta Mathematica Sinica, 2014, 57(2): 365-372. |
| [16] |
马国栋, 简金宝, 江羡珍. 一个具有下降性的改进Fletcher-Reeves共轭梯度法[J]. 应用数学学报, 2015, 38(1): 89-97. MA G D, JIAN J B, JIANG X Z. An improved Fletcher-Reeves conjugate gradient method with descent property[J]. Acta Mathematicae Applicatae Sinica, 2015, 38(1): 89-97. |
| [17] |
ZHANG B X, ZHU Z B, LI S A. A modified spectral conjugate gradient projection algorithm for total variation image restoration[J]. Applied Mathematics Letters, 2014, 27: 26-35. DOI:10.1016/j.aml.2013.08.006 |
| [18] |
ZHANG B X, ZHU Z B, WANG S. A simple primal-dual method for total variation image restoration[J]. Journal of Visual Communication and Image Representation, 2016, 38: 814-823. DOI:10.1016/j.jvcir.2016.04.025 |
| [19] |
ZHANG B X, ZHU Z B. A modified quasi-Newton diagonal update algorithm for total variation denoising problems and nonlinear monotone equations with applications in compressive sensing[J]. Numerical Linear Algebra with Applications, 2015, 22(3): 500-522. DOI:10.1002/nla.v22.3 |
| [20] |
曹莉, 王伟. 求解非线性不适定问题的连续Landweber型正则化方法[J]. 黑龙江大学自然科学学报, 2014, 31(2): 165-170. CAO L, WANG W. Continuous Landweber type regularization method for solving nonlinear ill-posed problem[J]. Journal of Natural Science of Heilongjiang University, 2014, 31(2): 165-170. |
| [21] |
VOGEL C R. Computational Methods for Inverse Pro-blems[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2011: 1-11.
|
 2016, Vol. 23
2016, Vol. 23 


