2. 广西大学亚热带农业生物资源保护与利用国家重点实验室,广西 南宁 530004;
3. 广西医科大学信息与管理学院,广西 南宁 530021
2. State Key Laboratory for Conservation and Utilization of Subtropical Agro-bioresources, Guangxi University, Nanning, Guangxi, 530004, China;
3. School of Information and Management, Guangxi Medical University, Nanning, Guangxi, 530021, China
【研究意义】蛋白质是组成生物的基础物质之一,蛋白质与蛋白质间相互作用所产生的功能对生命有重要意义,如DNA的合成、基因转录、蛋白质运输、信号转导等,但并非所有的蛋白质之间都能结合发生相互作用。研究蛋白质的交互作用对药物设计有很大的帮助。药物设计方法比较多样,比如计算诱变、分子对接以及从头设计等等,但这些方法都很难预测药物相互作用的过程,如果选择的两种蛋白质之间结合自由能很低的话,它们之间的相互作用就越低。此外,蛋白质交互[1]的细微变化都有可能改变复合物的功能,甚至给病人带来危害[2]。因此,通过计算预测蛋白质之间的自由能,对提高药物设计的效率以及理解蛋白质交互功能都有重大作用。【前人研究进展】近些年来,计算自由能的方法都是以提高预测精度和减少计算开销为目的。尽管一些方法能够比较准确地预测自由能,但是往往他们都有巨大的空间和时间开销,并且使用有局限的实验集。这些方法大致分为3大类:精确方法、终点法、经验公式。典型的精确方法有自由能微扰[3](Free Energy Perturbation,FEP)和热力学积分(Thermodynamic Integration,TI)[4]。FEP和TI都是典型的计算自由能的精确方法,但是它们都需要一定的计算时间,并且只能使用在结合和未结合状态[5]上平均信息熵变化小的蛋白质上,有很大的局限性。基于经验力场公式的终点法计算速度快,例如线性交互能方法(Linear Interaction Energy,LIE)[6]和Molecular Mechanics Poisson-Boltzmann Surface Area方法(MM-PBSA)[3]。LIE能计算蛋白质的结合和非结合状态下的平均静电和范德尔瓦斯交互自由能,它使用参数α和β来确定溶剂状态和蛋白质状态的内部势能的变化,但是参数值极易被不同的训练集影响。MM-PBSA分解结合自由能为△EMM、△Gsol、T△S,然后计算不同状态下蛋白质的不同自由能。但是,MM-PBSA不适合在那些构象熵变化特别大的蛋白质上,因此它们的误差很大。由于上述方法的局限性,现在很多研究基于蛋白质特征建立模型来预测自由能。此类方法的模型计算精度有很大的提升,而且计算时间大大减少。但是预测结果依然不完美,而且许多与自由能相关的特征都被忽略。有的方法是计算200个蛋白质结构特征[7]构建回归模型,从而预测蛋白质自由能。但是这个回归模型中的许多蛋白质结构特征以不同的方式被重复计算,而且有些特征计算开销大、时间长,无关特征和冗余特征会影响预测模型的精度。因此,需要对特征集合使用最小冗余最大相关算法[8]进行筛选。除结构特征,也有些研究使用序列特征来预测自由能[9]。尽管序列特征能够提高模型的表现,但是结构特征却使用很少;另外他们没有使用信息增益或其他可靠的方法对特征进行选择。同时, 因为使用的数据集较小,很多算法的模型并没有对特征重要性进行评估,这些训练样本过小以及未经过特征筛选的模型很容易过拟合。因此在模型构建上,有效的特征选择和特征重要性评估对蛋白质之间自由能预测特别重要。【本研究切入点】收集135对标有结合前后蛋白质变化的复合物,同时计算和选择那些与蛋白质自由能相关的结构特征和序列特征[10],并对特征进行选择和重要性分析。【拟解决的关键问题】首先使用Minimum Redundancy Maximum Relevance(mRMR)特征选择方法除去不相关特征以及冗余特征,从而获得最好的特征集;然后建立6种回归模型并通过10折交叉验证进行对比来选择最佳的模型;最后对选择后的结构特征进行移除特征分析,判断和确定结构特征对模型性能的重要性,从而证明mRMR特征选择的意义; 并用该模型训练和预测训练集135对蛋白质的自由能, 然后与他人所建立的模型进行对比。
1 材料与方法 1.1 数据预处理从文献[7]中收集135对蛋白质复合物,用于训练回归模型。每一对复合物都由2个蛋白质组成,每个蛋白质的氨基酸链都已经标出。根据功能分为9类:13个抗体-抗原类(A),5个抗原-结合抗体类(AB),34个酶-抑制剂类(EI),10个酶-底物类(ES),11个有调节和附件链的酶(ER),16个G-蛋白质(OG),12个受体(OR),34个混杂蛋白质(OX)。这些复合物都含有真实的来自实验结果的自由能(表 1)。
| 表 1 135对蛋白质复合物的蛋白质编号、功能类型和自由能 Table 1 Protein ID, functional class and free energy value of 135 protein complexes |
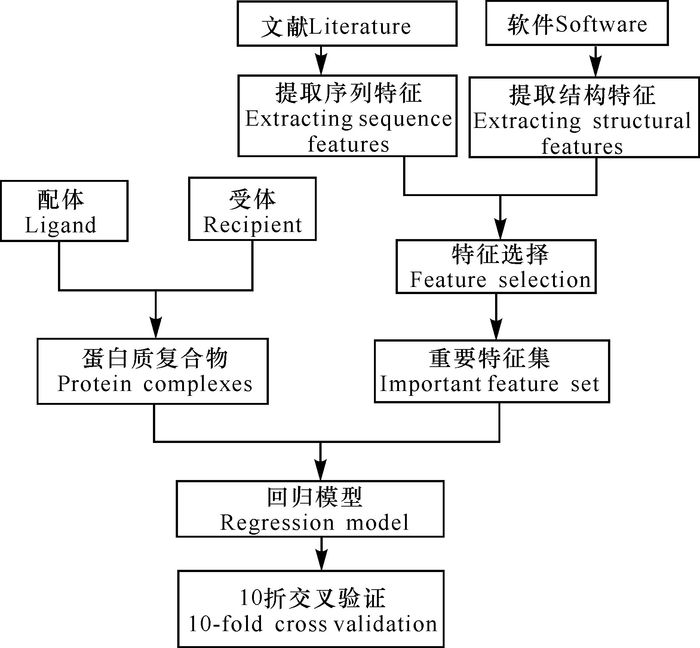
如图 1所示,本实验主要分为5步:第一步是收集蛋白质复合物和特征数据;第二步是提取并计算序列和结构特征值;第三步是使用mRMR进行特征选择,从而得到最有价值的特征集;第四步是建立6种回归模型并进行10折交叉验证,通过最高相关性和最小Mean Absolute Error(MAE)来选择最佳模型;第五步通过特征移除分析进一步证明特征价值。
|
图 1 实验流程图 Fig.1 The flow chart of experiment |
(1) 序列特征计算
从2篇文献中共收集592种氨基酸的值(氨基酸的值代表不同环境下测试的氨基酸能量)。其中544种氨基酸的值来自AAindex数据库[11],剩下的48种氨基酸的值来自Gromiha[12]的研究。将蛋白质的氨基酸序列进行统计,得到每种氨基酸的数量,再将每种氨基酸的数量乘以对应的氨基酸的值,将相乘后得到的数相加便是蛋白质序列特征值。最终得到592个序列特征值。
(2) 结构特征计算
原子表面积(Accessible Surface Area,ASA)的计算是基于NACCESS[13]软件,通过旋转一个1.4 Å半径探针原子在蛋白质表面计算。将一对蛋白质结合前的ASA减去结合后形成复合物的ASA便得到△ASA。得到的△ASA的值越大,就越说明减少的表面积越多,相互作用接触的面积越多。
通过文献作者提供的Vangone[14-15]软件来计算接触的残基(ICs)的数量和非相互作用的表面(NIS)的比例,根据得到的结果进行分类。对于ICs得到带电-带电、带电-非极性、极性-极性、极性-非极性4种类型的数量作为特征,对于NIS得到带电、非极性、极性3种类型的比例作为特征。
1.2.3 特征选择和回归模型将得到的序列特征和结构特征使用最小冗余最大相关(mRMR)算法进行过滤。mRMR算法一共分为2步:根据相关性系数r来计算特征与蛋白质自由能之间的相关性,将非显著相关的特征作为不相关特征除去;再对特征与特征之间相关性进行计算,如果相关性为1,说明这2个特征是同一种特征,因此去掉其中一个冗余特征,从而得到更加完善的特征集。这样得到的特征集是最小冗余最大相关特征。
| $r=\frac{\sum\limits_{i=1}^{n}{\left( Xi-\bar{X}\text{ } \right)}\left( Yi-\bar{Y} \right)}{\sqrt{\sum\limits_{i=1}^{n}{{{\left( Xi-\bar{X} \right)}^{2}}~}}\sqrt{\sum\limits_{i=1}^{n}{{{\left( Yi-\bar{Y} \right)}^{2}}}}}~。$ |
使用经过特征选择后的特征集建立回归模型,并预测蛋白质自由能。所建立的6种回归模型分别是Support Vector Regression (SVR),Radial Basis Function Network(RBF network),Linear Regression,Sequential Minimal Optimization Regression (SMOreg),Additive Regression,Regression By Discretization。此外,对每种模型进行10折交叉验证来检测性能,然后选取性能最佳的模型来预测蛋白质自由能。对于回归模型性能的判断,选择相关系数r和平均绝对误差(MAE)。
| $\text{MAE}=~\frac{1}{n}\sum \left| Xi-\bar{X} \right|。$ |
特征对模型[16]的性能有一定的影响,一个好的特征往往对模型性能的提高起到一定的作用。因此,当一个好的特征被移除时,模型的性能可能会降低。通过移除每个结构特征,对比移除该特征前后模型性能的变化来判断该结构特征对模型的价值。每次移除一个结构特征,将剩下的特征作为特征集来建立回归模型,然后对比移除前后性能的变化来判断该特征对模型的价值。对比过后再将特征放回到特征集中,移除另一个结构特征直到所有特征都被移除,从而对结构特征进行移除分析。其结果显示当结构特征被移除后回归模型的相关性有所降低。
2 结果与分析通过最小冗余最大相关(mRMR)算法对得到的序列特征和结构特征进行过滤,最终得到45个序列特征和5个结构特征(表 2)。
| 表 2 45个序列特征和5个结构特征 Table 2 45 sequence features and 5 structure features |
通过mRMR来选择有价值的特征之后,将这些特征投入来建立6种回归模型来预测蛋白质自由能,并将这些模型通过10折交叉验证,表 3中显示的是6种模型通过10折交叉验证后的性能。其中模型性能最好的是Linear Regression模型,它的10折交叉验证的性能明显比其他算法更加优越,其相关系数达到0.502 9,比其它算法高;它的MAE为1.973 8 kcal·mol-1,比其它算法都低。被选择的5个结构特征与蛋白质自由能具有显著性相关,表 4显示他们有着很高的相关性和很低的P值。
| 表 3 6种模型基于10折交叉验证后的性能 Table 3 The performance of 6 regression models are based on 10-fold cross-validation |
| 表 4 5个结构特征与蛋白质自由能之间的相关性和P值 Table 4 The correlation coefficient and P value between five structure features and protein free energy |
将选择后的5个结构特征进行移除分析,观察移除后Linear Regression模型的10折交叉性能。表 5显示移除每个结构特征后Linear Regression模型的相关性和MAE的值, 从中可以看到相对于原来Linear Regression的相关性0.502 9,移除后相关性有着明显的降低。
| 表 5 结构特征移除后的Linear Regression模型基于10折交叉验证的性能 Table 5 The performance of 10-fold cross-validation of Linear Regression using feature set by pruning structure features |
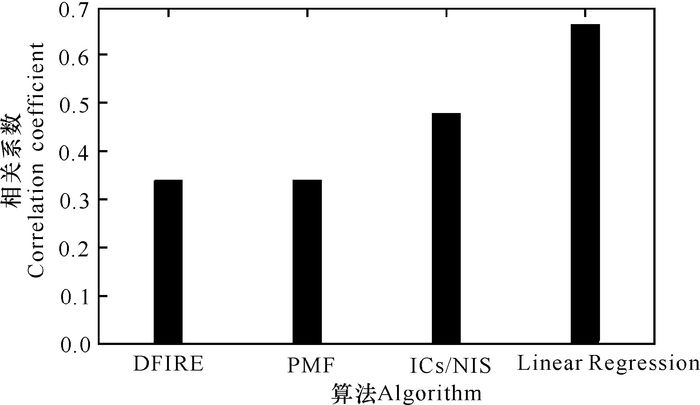
从DFIRE[17],PMF[18]和ICs/NIS[14]提供的方法来预测135对蛋白质复合物的自由能。如图 2所示,Linear Regression模型预测结果相关系数为0.66,DFIRE和PMF为0.34,ICs/NIS为0.48。从相关系数来看,Linear Regression模型有着更好的性能。相关性越大,说明模型与蛋白质自由能有着很强的关联。此外,Linear Regression模型性能在平均绝对误差上也是比较优秀的,该模型的误差为1.973 8 kcal·mol-1,DFIRE为4.82 kcal·mol-1,PMF为3.22 kcal·mol-1,ICs/NIS为1.893 7 kcal·mol-1。平均绝对误差越小,说明在预测蛋白质自由能的值上,预测的结果可以更加精确,所造成的误差更小。
|
图 2 线性回归算法与其它方法性能的对比 Fig.2 Performance comparison between Linear Regression algorithm and other methods |
最近几年,越来越多与蛋白质自由能相关的特征被计算出来。在此基础上,本研究提出一种基于序列和结构特征的蛋白质自由能预测方法:在特征计算上,计算蛋白质序列特征和结构特征;在特征选择上,使用mRMR来选择重要的特征,使得被筛选后的特征达到最小冗余最大相关,从而确保模型更加精确;在特征分析上,通过计算该特征移除前后模型性能的变化来判断该特征的价值,实验结果显示结构特征能提高模型的性能;在模型选择上,本研究建立多种模型基于10折交叉验证,通过选择最高相关性和最低平均绝对误差来选择最准确最可靠的模型;最终,将模型的性能与其它方法进行对比,得到基于序列特征和结构特征的Linear Regression模型,相对其他模型有着更准确的性能,其相关性为0.66,MAE为1.973 8 kcal·mol-1。
| [1] |
VIDAL M, CUSICK M E, BARABÁSI A L. Interactome networks and human disease[J]. Cell, 2011, 144(6): 986-998. DOI:10.1016/j.cell.2011.02.016 |
| [2] |
CHEN Q F, LUO H Q, ZHANG C Q, et al. Bioinformatics in protein kinases regulatory network and drug discovery[J]. Mathematical Biosciences, 2015, 262: 147-156. DOI:10.1016/j.mbs.2015.01.010 |
| [3] |
GILSON M K, ZHOU H X. Calculation of protein-ligand binding affinities[J]. Annual Review of Biophysics and Biomolecular Structure, 2007, 36(1): 21-42. DOI:10.1146/annurev.biophys.36.040306.132550 |
| [4] |
BORDNER A J, MITTELMANN H D. Prediction of the binding affinities of peptides to class Ⅱ MHC using a regularized thermodynamic model[J]. BMC Bioinformatics, 2010, 11: 41. DOI:10.1186/1471-2105-11-41 |
| [5] |
CHEN Q F, CHEN Y P P. Function annotation for pseudoknot using structure similarity[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2011, 8(6): 1535-1544. DOI:10.1109/TCBB.2011.50 |
| [6] |
HANSSON T, MARELIUS J, ÅQVIST J. Ligand binding affinity prediction by linear interaction energy methods[J]. Journal of Computer-Aided Molecular Design, 1998, 12(1): 27-35. DOI:10.1023/A:1007930623000 |
| [7] |
MOAL I H, AGIUS R, BATES P A. Protein-protein binding affinity prediction on a diverse set of structures[J]. Bioinformatics, 2011, 27(21): 3002-3009. DOI:10.1093/bioinformatics/btr513 |
| [8] |
YU L, LIU H.Feature selection for high-dimensional data:A fast correlation-based filter solution[C]//Proceedings of the 20th International Conference on Machine Learning.Washington, DC:ICML, 2003.
|
| [9] |
YUGANDHAR K, GROMIHA M M. Protein-protein binding affinity prediction from amino acid sequence[J]. Bioinformatics, 2014, 30(24): 3583-3589. DOI:10.1093/bioinformatics/btu580 |
| [10] |
CHEN Q F, LAN W, WANG J X. Mining featured patterns of miRNA interaction based on sequence and structure similarity[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2013, 10(2): 415-422. DOI:10.1109/TCBB.2013.5 |
| [11] |
KAWASHIMA S, POKAROWSKI P, POKAROWSKA M, et al. AAindex:Amino acid index database, progress report 2008[J]. Nucleic Acids Research, 2008, 36(S1): D202-D205. |
| [12] |
GROMIHA M M. A statistical model for predicting protein folding rates from amino acid sequence with structural class information[J]. Journal of Chemical Information and Modeling, 2005, 45(2): 494-501. DOI:10.1021/ci049757q |
| [13] |
HUBBARD S J, THORNTON J M.NACCESS 2.1.1.[R].London:Department of biochemistry and molecular biology, University College.
|
| [14] |
VANGONE A, BONVINA M J J. Contacts-based prediction of binding affinity in protein-protein complexes[J]. eLife, 2015, 4: e07454. |
| [15] |
KASTRITISP L, RODRIGUES J P G L M, FOLKERS G E, et al. Bonvin:Proteins feel more than they see:Fine-tuning of binding affinity by properties of the non-interacting surface[J]. Journal of Molecular Biology, 2014, 426(14): 2632-2652. DOI:10.1016/j.jmb.2014.04.017 |
| [16] |
CHEN Q F, CHEN Y P P. Mining protein kinases regulation using graphical models[J]. IEEE Transactions on Nano Bioscience, 2011, 10(1): 1-8. |
| [17] |
LIU S, ZHANG C, ZHOU H Y, et al. A physical reference state unifies the structure-derived potential of mean force for protein folding and binding[J]. Proteins:Structure, Function, and Bioinformatics, 2004, 56(1): 93-101. DOI:10.1002/prot.20019 |
| [18] |
SU Y, ZHOU A, XIA X F, et al. Quantitative prediction of protein-protein binding affinity with a potential of mean force considering volume correction[J]. Protein Science, 2009, 18(12): 2550-2558. DOI:10.1002/pro.v18:12 |
 2017, Vol. 24
2017, Vol. 24 


