2. 广西大学物理科学与工程技术学院,广西南宁 530004
2. School of Physical Science and Technology, Guangxi University, Nanning, Guangxi, 530004, China
【研究意义】近年来,车辆交通和行人交通的研究在物理科学领域受到广泛关注[1]。在车辆交通和行人交通中,许多被观察到的自组织现象已经通过运用物理、数学以及计算科学的理论与模拟方法成功再现[1]。随着人口和大型公共场所的迅速增多,高层建筑的不断涌现,地震、建筑物火灾以及人群踩踏突发事故的发生使得人们越来越关注人群的安全问题[1]。因此,疏散动力学的研究具有非常重要的现实意义,它的研究成果为行人避免踩踏事件及安全疏散起到重要的指导意义[1]。发达国家已投入大量资金用于行人交通流的研究,以避免突发事件的发生。【前人研究进展】近五十年来有众多的物理、力学、数学、计算机科学等领域的专家和研究学者从事行人交通流的研究,并取得大量具有创新性的研究成果[2-11],提出很多行人交通流模型,典型的有社会力模型[12]、元胞自动机模型[13-17]、智能模型[14]、格子气模型[17-18]等。岳昊等[19-20]建立用于模拟行人横向干扰、行人双向行走、行人正常情况下、行人视距受影响和安全出口处行人布局不平衡时的行人疏散元胞自动机模型,周金旺等[21]基于元胞自动机模拟研究成对行人结伴逃生对行人整体的影响。另外,也有有关室内行人之间的博弈、多出口室内行人对出口选择等疏散动力学的研究[22-23]。格子气模型因其简单方便而受到众多研究者的青睐,并发现很多研究成果如相变行为、瓶颈效应、标度关系、自组织现象等[2-17]。迄今为止,格子气模型广泛用于研究占据单个格点的行人运动和车辆行驶等。但是实际的交通流中每种移动物体的形状并不都是一样的,运动的个体具有各种各样的形状和相应大小,在行进过程不可能用占据单个格点时的情况来模拟。因此已经有研究对格子气模型进行扩展,如Muramatsu等[24],Nagai等[25]已经成功运用扩展的格子气模型研究细长条形状的机械物在通道中的相向流,并得到对实际具有指导意义的结果。【本研究切入点】由于行人的主观能动性,行人行走过程中有可能结对行走,例如一起出来玩耍的朋友或全家人出游倾向于一起行走,他们会在不知不觉中构成一个人群集团;又或者大型游戏过程中故意形成的人群集团一起竞赛等等,但是有关行人形成集团后一起行走的行为模拟成果不多。【拟解决的关键问题】本研究将从微观的角度,用扩展格子气模型来研究行人集团在通道中的行走行为,研究行人集团的平均速度和流量与行人集团密度的关系,同时还研究行人集团的尺度大小,通道的尺度大小和迁移概率对密度相变点的影响。
1 模型的扩张将单个格点的格子气模型扩展到占据多个格点的格子气模型。一个行人集团在二维网格上占据n1×n2个格点而且不能有重叠,考虑多个行人集团在通道内运动。
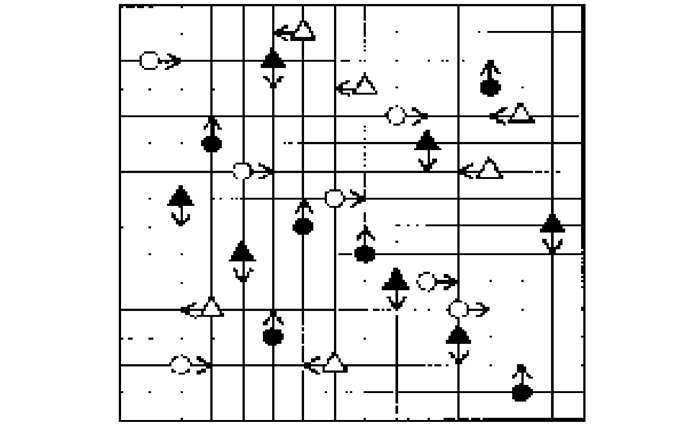
如图 1所示,该模型被定义在一个W×W的网格上,W表示通道的长和宽,该模型中包括4类人群,分别为左行人群、右行人群、上行人群和下行人群,图 1中空白圆表示右行人群,空白三角形表示左行人群,实心圆表示向上行走的人群,实心三角形表示向下行走的人群。边界采用周期边界条件,人群按照一定的行走规则行走,行走过程中行人集团不可重叠。
|
图 1 四向行人集团流在通道中的示意图 Fig.1 Sketch of four-way group flow on a channel |
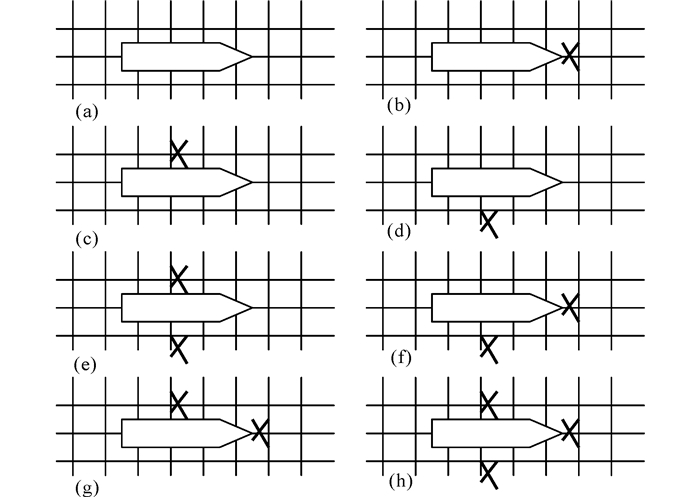
图 2表示占据4个格子的长条型行人集团右走的典型结构图。集团用一箭头表示,“×”表示该格点被其他集团占据(集团前方的“×”表示至少有一个格点被占据)所有的行人集团向空的目标格点移动不后退。每个行人集团均可以向附近的空格点移动:右行行人集团可以向右、向上和向下3个方向移动;左行行人集团可以向左、向上和向下3个方向移动;上行行人集团可以向上、向左和向右3个方向移动;下行行人集团可以向下、向左和向右3个方向移动。行人集团采取随机行走规则,往各个方向行走的概率由周围的结构决定。以右行行人集团为例,在不同的结构下往各个方向的行走概率pt, x, pt, y, pt, -y如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;{p_{t, y}} = {D_y} + \left( {1-D} \right)/3, {p_{t, x}} = {D_x} + \left( {1-D} \right)/3, \\ {p_{t, -x}} = \left( {1 - D} \right)/3; \end{array} $ | (1) |
| $ {p_{t, x}} = 0, {p_{t, y}} = 1/2, {p_{t, -y}} = 1/2; $ | (2) |
| $ \begin{array}{l} \;\;\;\;\;\;{p_{t, x}} = D + \left( {1-D} \right)/2, {p_{t, y}} = 0, {p_{t, -y}} = \\ \left( {1-D} \right)/2; \end{array} $ | (3) |
| $ {p_{t, x}} = D + \left( {1-D} \right)/2, {p_{t, y}} = \left( {1-D} \right)/2, {p_{t-y}} = 0; $ | (4) |
| $ {p_{t, y}} = 1, {p_{t, x}} = 0, {p_{t, -x}} = 0; $ | (5) |
| $ {p_{t, y}} = 0, {p_{t, x}} = 0, {p_{t, -x}} = 1; $ | (6) |
| $ {p_{t, y}} = 1, {p_{t, x}} = 1, {p_{t, -x}} = 0; $ | (7) |
| $ {p_{t, y}} = {p_{t, x}} = {p_{t, -x}} = 0。$ | (8) |
|
图 2 占据四个格子的行人集团右走的典型结构 Fig.2 Typical patterns of rightward pedestrian group to occupy four lattices |
其中D表示向出口的迁移概率。在每一个单位时步内,所有的行人集团看作一个整体更新一次,采用随机顺序更新规则。行人集团同时向左、向右、向上、向下4个方向运动。需要特别说明的是,上行和下行的行人集团其形状规则在行走过程中均与左行和右行的行人集团一样,也就是行走过程中始终与图 2的集团摆向一致,这其实与Nagai等[25]的细长移动物体在通道中的相向流动大致上是一样的。
2 计算机模拟我们用计算机来模拟行人集团在通道中的行走过程。初始的时候,N个人随机分布在通道内,每个格子的状态或为空,或被一个人占据着,每个时步对应1 s。往4个方向运动的行人人数均为N/4,模拟中的右行、左行、上行和下行行人分别用空白圆、空白三角形、实心圆和实心三角形表示。用Nl来表示集团的长度,为能很好地描述具有一定尺度的行人集团的特性,在统计流量和平均速度时用占有率C(C=N×Nl/(W×W))来代替密度P(P=C/Nl)。采用随机顺序更新。在时间t=0的时刻,所有的人都静止;当时间t>0时,所有人群按照以上规则进行更新,行人在通道中的最大速度vmax=1。当所有的人都更新以后,一个时步完成,然后进行下一个时步。在模拟过程中,前104时步不作计算以消除暂态的影响,后104时步开始进行统计,模拟结果取样本数30平均所得。本研究长度单位均以格点为单位,采用无量纲化计算。
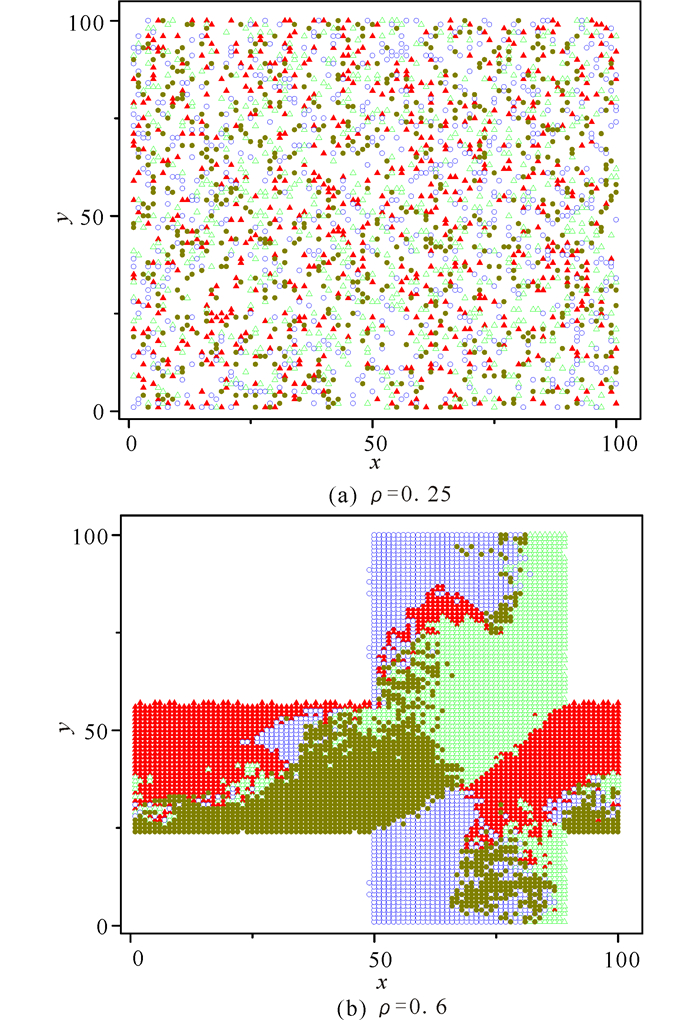
3 结果与分析 3.1 单个行人和行人集团的演化斑图从图 3中我们看到,占据1个格点的单个行人在密度比较低(ρ=0.25) 的情况下,可以自由运动;在密度较高(ρ=0.6) 的情况下时,完全阻塞出现,往4个方向行走的行人互相阻碍导致无法前行。此时可以看到两种交通状态出现:(a)自由交通和(b)阻塞交通。
|
图 3 单个行人交通的演化斑图(w=100,D=0.0,T=104) Fig.3 Evolution pattern of single pedestrian traffic (w=100, D=0.0, T=104) |
而从图 4中可以看出,在密度ρ=0.6的情况下,与图 3b单个行人行走的情况不一样,此时只是出现局域堵塞的现象,但是仍然有许多可以自由行走的行人集团,并没有造成完全的堵塞;但在密度更高(ρ=0.8) 的情况下也出现了完全堵塞。因此,与占据1个格点的单个行人相比较,占据5个格点的行人集团相对来说不容易形成堵塞。

|
图 4 占据5个格点的行人集团的演化斑图(w=100,D=0.0,T=104) Fig.4 Evolution pattern of pedestrian group to occupy five points(w=100, D=0.0, T=104) |
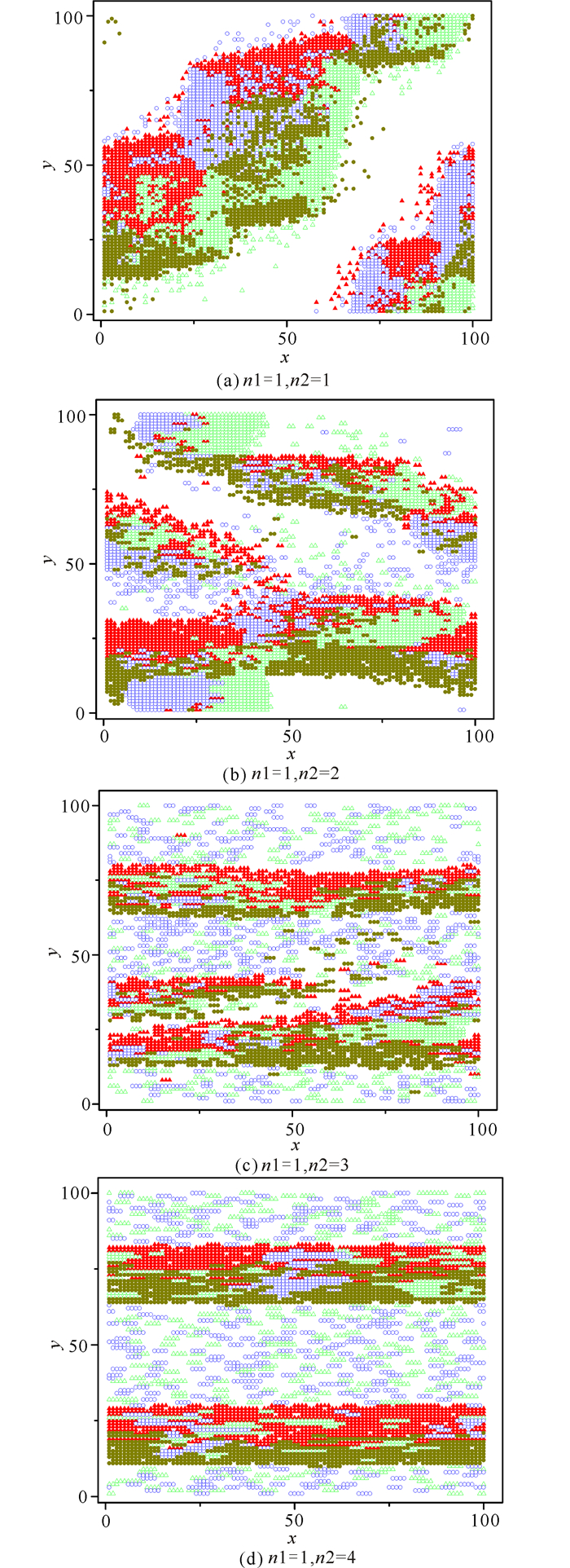
由图 5中可知,随着行人集团尺度的增大,在同样条件下可以自由运动的行人集团就会越多,会有更多的行人穿过集群阻塞区域,行人集团的尺度越长就越容易躲避与他们行走方向相反的行人集团,反而越不容易形成堵塞。
|
图 5 对应不同尺度的行人集团的堵塞演化斑图(w=100,D=0.0,T=104,ρ=0.52) Fig.5 Evolution blocking patterns of pedestrian group corresponding to the different size(w=100, D=0.0, T=104, ρ=0.52) |
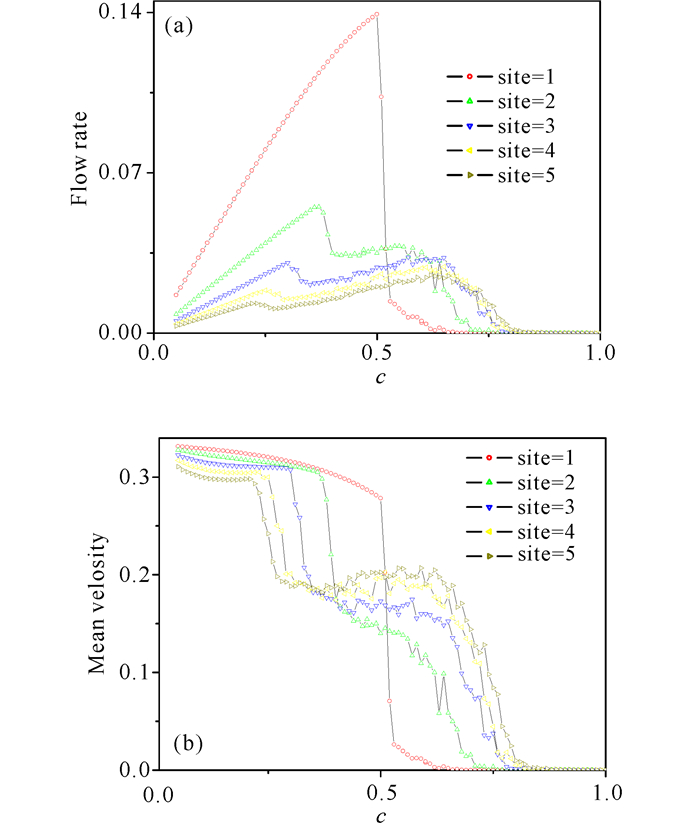
图 6a是流量随占有率的变化图,展示行人集团尺度从1变到5,即n1=1,n2=1,2,3,4,5的流量图。在低密度范围内,不同尺度的行人集团均流量随占有率线性增加,但是只占据单个格点的行人(n1=1,n2=1) 流量在达到最大值后,大概在ρ=0.5处流量值突然掉下,最后降为零,形成完全堵塞的状态。而n1=1, n2=2,3,4,5的情况则有所不同,流量先随着占有率的增大而增大,然后才随着占有率的增大而减小,最后减小到零,形成堵塞状态。达到堵塞状态的占有率(密度)的临界值随着行人集团尺度的增大而增大,这也说明行人集团尺度越大,形成堵塞的可能性越弱。图 6b是平均速度随占有率(密度)的变化图,每条平均速度曲线均与图 6a中的流量曲线相对应,平均密度随着占有率(密度)的增大而减小,最后随着占有率(密度)的增大减小到零。但是平均速度的最大值随着集团尺度的增大而减小。
|
图 6 不同行人集团尺度的流量(a)和平均速度(b)与占有率的关系(w=100,D=0.0,T=104) Fig.6 Relation of flow rate(a) and mean velocity(b) of pedestrian group with different size vs occupancy(w=100, D=0.0, T=104) |
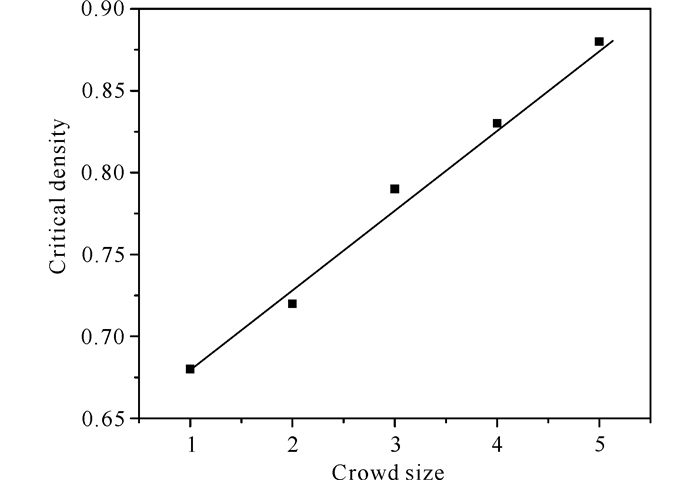
如图 7所示,临界密度几乎是随着行人集团尺度的增加而线性增大的,从而说明阻塞相变与行人集团尺度具有很大的关系。
|
图 7 临界密度与集团尺度n之间的关系(w=100,D=0.0,T=104) Fig.7 Relation of group size n with critical density(w=100, D=0.0, T=104) |
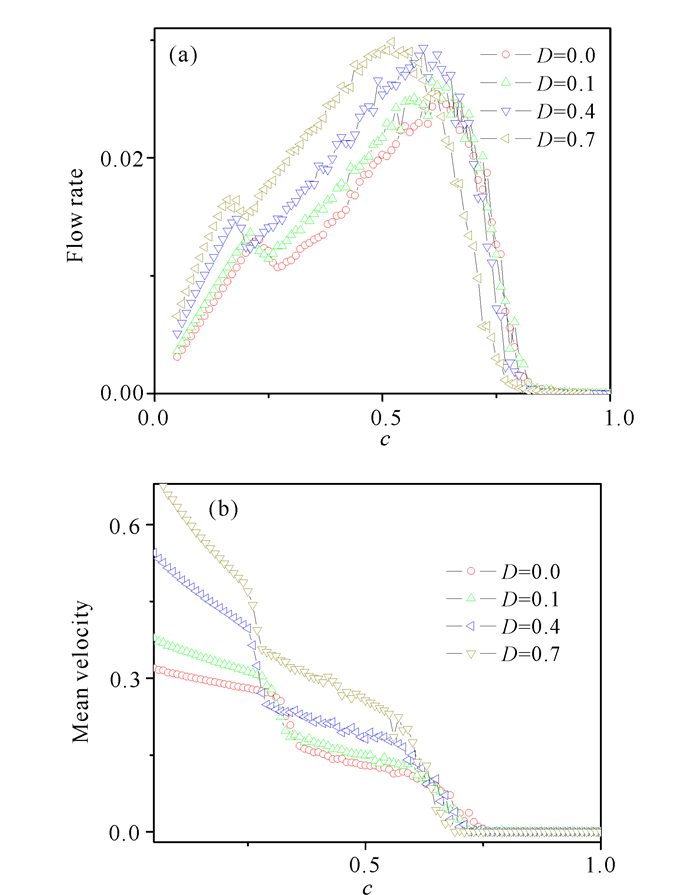
图 8a、b分别展示D=0.0,0.1,0.4,0.7,w=100,行人集团尺度为5时行人流量、平均速度与占有率的关系。从图 8a中可以看到,在低密度(占有率)范围内,不同尺度的行人流量随占有率线性增加,流量第一次达到较小的最大值后降下来,达到一个较小值后又随着占有率的增大而增大,第二次达到一个峰值,然后才随着占有率的增大而减小,最后减小到零,达到堵塞状态。达到堵塞状态的临界密度(占有率)随D的变化不大,且两次达到的最大值均随着迁移概率(D)的增加而增大。图 8b中的每条曲线均与图 8a中的每条曲线相对应,在低占有率区域每条速度曲线随着占有率增加下降较快,然后在密度增大一些后下降得较为缓慢些,最后下降到零。同样地,临界密度受D的影响不是很明显。
|
图 8 行人集团在不同的迁移概率D下的流量(a)和平均速度(b)与占有率的关系 Fig.8 Relation of flow rate(a) and velocity (b) under the straight probability D of pedestrian group with occupancy |
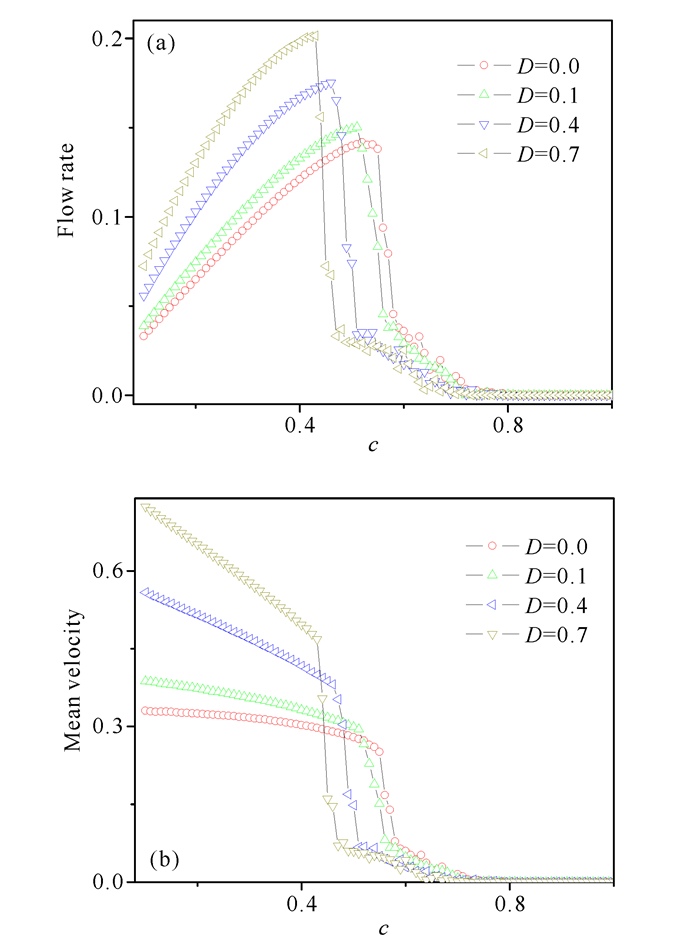
由图 9可见,在单个行人的情况下,行人流量和平均速度的最大值均随着D的增大而增大。与图 8a不同的是,图 9a中对应的每一条流量曲线中,在低占有率自由流区域均随着密度的增大而线性增大,然后在较高密度区域流量随着密度的增大而减小,直到减小到零。平均速度则是随着占有率的增大而减小,直到减小到零。由于在堵塞区域占据单个格点的单个行人均不可以移动,因此在高密度堵塞区域,流量和平均速度均不随着D的增大而增大。
|
图 9 行人集团在不同迁移概率D下的流量(a)和平均速度(b)与占有率的关系(D=0.0, 0.1, 0.4, 0.7,w=100) Fig.9 Relation of flow rate(a) and velocity (b) under the straight probability D of pedestrian group with occupancy(D=0.0, 0.1, 0.4, 0.7, w=100) |
本研究用扩展的格子气模型研究组成集团的行人在通道中的运动情况,行人集团的尺度由原来的单个行人扩展到占据n1×n2个格点的行人集团。模拟结果表明,行人集团的尺度对阻塞演化斑图的影响很大,行人集团的尺度越大,越不容易形成堵塞;从自由相到堵塞相的相变临界密度随着行人集团的尺度的增加而线性增大。同时,迁移概率D对行人的流量和平均速度均有较大的影响。由于本研究所用的模型与Nagai等[25]研究细长机械移动物体所用的模型一样,且四向行人集团的行走规则与细长机械移动物体在通道中相向行走的规则也一样,因此得到与他们类似的模拟结果。如果四向长条型行人集团的行走方向在左、右方向沿水平方向运动,而在上、下方向沿竖直方向运动,则期望看到的模拟结果与本研究的结果不同,沿四个方向运动的长条型行人集团由于其体积效应而容易形成交通阻塞。
| [1] |
杨立忠, 方伟峰, 黄锐, 等. 基于元胞自动机的火灾中人员逃生的模型[J]. 科学通报, 2002, 47(12): 896-901. YANG L Z, FANG W F, HUANG R, et al. Occupant evacuation model based on cellular automata in fire[J]. Chinese Science Bulletin, 2002, 47(12): 1484-1488. |
| [2] |
SOBEL R S, LILLITH N. Determinant of nonstationary personal space invasion[J]. The Journal of Social Psychology, 1975, 97(1): 39-45. DOI:10.1080/00224545.1975.9923310 |
| [3] |
陈然, 董力耘. 中国大都市行人交通特征的实测和初步分析[J]. 上海大学学报:自然科学版, 2005, 11(1): 93-97. CHEN R, DONG L Y. Observations and preliminary analysis characteristics of pedestrian traffic in Chinese metropolis[J]. Journal of Shanghai University:Natural Science, 2005, 11(1): 93-97. |
| [4] |
HENDERSON L F. The statistics of crowd fluids[J]. Nature, 1971, 229(5284): 381-383. DOI:10.1038/229381a0 |
| [5] |
HELBING D. A fluid-dynamic model for the movement of pedestrians[J]. Complex System, 1992, 6(5): 391-415. |
| [6] |
HOOGENDOORN S, BOVY P. Gas-kinetic modeling and simulation of pedestrian flows[J]. Transportation Research Record:Journal of the Transportation Research Board, 2000, 1710: 28-36. DOI:10.3141/1710-04 |
| [7] |
田欢欢. 行人格子流体力学模型、信息疏散作用及交通能耗的研究[D]. 南宁: 广西大学, 2009. TIAN H H.Lattice hydrodynamic model of pedestrian flow, influence of information on evacuation process and energy dissipation of mixing traffic flow[D]. Nanning:Guangxi University, 2009. |
| [8] |
HELBING D, MOLNÁR P. Social force model for ped-estrian dynamics[J]. Physical Review E, 1995, 51(5): 4282-4286. DOI:10.1103/PhysRevE.51.4282 |
| [9] |
田欢欢, 董力耘, 薛郁. 基于非对称作用的二维优化速度改进模型[J]. 广西科学, 2015, 22(4): 357-361. TIAN H H, DONG L Y, XUE Y. Improved two-dimensional optimal velocity model based on asymmetric interaction[J]. Guangxi Sciences, 2015, 22(4): 357-361. |
| [10] |
白克钊, 蔡美静, 许志鹏, 等. 中心护栏对行人交通流的影响研究[J]. 广西科学, 2015, 22(4): 368-372. BAI K Z, CAI M J, XU Z P, et al. Effect of central barrier on pedestrian traffic flow[J]. Guangxi Sciences, 2015, 22(4): 368-372. |
| [11] |
夏玉显, 薛郁, 梁玉娟, 等. 适应性交通流连续性模型[J]. 广西科学, 2015, 22(4): 382-387-387. XIA Y X, XUE Y, LIANG Y J, et al. Adaptive traffic continuum model[J]. Guangxi Sciences, 2015, 22(4): 382-387-387. |
| [12] |
OKAZAKI S. A study of pedestrian movement in architectural space, part 1:Pedestrian movement by the application on of magnetic models[J]. Transactions of the Architectural Institute of Japan, 1979, 283: 111-119. DOI:10.3130/aijsaxx.283.0_111 |
| [13] |
BLUE V J, ADLER J L.Bi-Directional emergent fundamental pedestrian flows from cellular automata microsimulation[C]//Proceedings of the 14th International Symposium on Transportation and Traffic Theory.Jerusalem, Israel:Pergamon.1999:235-254. https://trid.trb.org/view/656759
|
| [14] |
SONG W G, XU X, WANG B H, et al. Simulation of evacuation processes using a multi-grid model for pedestrian dynamics[J]. Physica A:Statistical Mechanics and Its Applications, 2006, 363(2): 492-500. DOI:10.1016/j.physa.2005.08.036 |
| [15] |
FUKUI M, ISHIBASHI Y. Jamming transition in cellular automaton models for pedestrians on passageway[J]. Journal of the Physical Society of Japan, 1999, 68(11): 3738-3739. DOI:10.1143/JPSJ.68.3738 |
| [16] |
SCHADSCHNEIDER A.Cellular automaton approach to pedestrian dynamics-theory[M]//SCHRECKENBERG M, SHARMA S D (eds.).Pedestrian and Evacuation Dynamics.Berlin:Springer, 2002:75-77.
|
| [17] |
MURAMATSU M, IRIE T, NAGATANI T. Jamming transition in pedestrian counter flow[J]. Physica A:Statistical Mechanics and Its Applications, 1999, 267(3/4): 487-498. |
| [18] |
WANG H N, CHEN D, PAN W, et al. Evacuation of pedestrians from a hall by game strategy update[J]. Chinese Physics B, 2014, 23(8): 080505. DOI:10.1088/1674-1056/23/8/080505 |
| [19] |
YUE H, HAO H R, CHEN X M, et al. Simulation of pedestrian flow on square lattice based on cellular automata model[J]. Physica A:Statistical Mechanics and its Applications, 2007, 384(2): 567-588. DOI:10.1016/j.physa.2007.05.070 |
| [20] |
岳昊, 邵春福, 陈晓明, 等. 基于元胞自动机的对向行人交通流仿真研究[J]. 物理学报, 2008, 57(11): 6901-6908. YUE H, SHAO C F, CHEN X M, et al. Simulation of bi-directional pedestrian flow based on cellular automata model[J]. Acta Physica Sinica, 2008, 57(11): 6901-6908. DOI:10.7498/aps.57.6901 |
| [21] |
周金旺, 邝华, 刘慕仁, 等. 成对行为对行人疏散动力学的影响研究[J]. 物理学报, 2009, 58(5): 3001-3007. ZHOU J W, KUANG H, LIU M R, et al. Paired behavior effect on pedestrian evacuation dynamics[J]. Acta Physica Sinica, 2009, 58(5): 3001-3007. DOI:10.7498/aps.58.3001 |
| [22] |
XU Y, HUANG H J, TIAN L J.Simulation of exit choosing in pedestrian evacuation using a cellular automaton model based on surrounding pedestrian density[C]//Proceedings of 2011 Fourth International Joint Conference on Computational Sciences and Optimization.Yunnan:IEEE, 2011:1109-1112. http://dl.acm.org/citation.cfm?id=2005139
|
| [23] |
刘泽高, 陈栋, 薛郁. 多出口室内行人出口选择行为研究[J]. 广西科学, 2015, 22(4): 388-394. LIU Z G, CHEN D, XUE Y. Behavior study on exit choice of indoor pedestrians in multiple exits[J]. Guangxi Sciences, 2015, 22(4): 388-394. |
| [24] |
MURAMATSU M, NAGATANI T. Jamming transit-ion in two-dimensional pedestrian traffic[J]. Physica A:Statistical Mechanics and Its Applications, 2000, 275(1/2): 281-291. |
| [25] |
NAGAI R, NAGATANI T. Jamming transition in counter flow of slender particles on square lattice[J]. Physica A:Statistical Mechanics and Its Applications, 2006, 366: 503-512. DOI:10.1016/j.physa.2005.10.040 |
 2017, Vol. 24
2017, Vol. 24 


