【研究意义】随着科技的飞速发展以及人类生产力的不断进步,如何更好地开发利用资源以解决能源的巨大需求,成为社会继续发展的一大问题。太阳辐射到地球上的能量大约是人类能源消耗的几千倍,且清洁环保,因此太阳能是代替化石能源的优秀选择之一,如果能够充分利用,能源问题以及化石材料燃烧引发的环境问题都将迎刃而解。1994年4月,日本全国的电力公司宣布同意购买个人发电的剩余部分。同年6月,日本通产省公布了日本21世纪的能源、住宅、建筑产业的行动方针修改大纲,其中强调了太阳能发电能起到保护地球环境和代替石油等能源的两个作用,并且增加了一项政策:给安装太阳能发电系统的用户提供资金补助[1]。从20世纪90年代以来,我国在太阳能光伏发电的领域进步比较快,光伏组件的生产能力在不断的增强,太阳电池的研究已经经历了几次更新换代,其中,以包括GaN、AlGaN、InGaN等在内的Ⅲ族氮化物半导体材料的出现,为第三代太阳电池和紫外探测器的相关研究提供了新的思路[2]。GaN属于直接宽带隙半导体材料,纤锌矿结构带隙3.4 eV(300 K),很适合制作紫外、蓝绿光发射装置[3]。InxGa1-xN材料可以通过改变In元素的含量,实现从InN的带隙到GaN的带隙(即0.7~3.4 eV)的连续可调,用InGaN材料制备的太阳能电池的可吸收光波长几乎覆盖整个太阳光谱,这些独特的宽带隙优势,使Ⅲ族氮化物适合制备各种颜色的LED以及全光谱太阳电池[4]。InGaN材料具有光吸收系数高(达到10-5 cm-1)、耐高温、抗辐射性好等特点,已成为制备太阳电池的理想材料[5]。因此,将InGaN材料进行不同组分的合理带隙叠层配备,可以使太阳电池获得较高的光电转换效率。【前人研究进展】国际上Jani等[6]和Neufeld等[7]采用金属有机物化学气相沉积(MOCVD)技术制备了p-i-n型InGaN/GaN异质结太阳电池,测得太阳电池的外量子效率分别为43%和63%。虽然所得量子效率较高,但开路电压约为2 V,且太阳电池中InGaN层的In组分较低,在15%以下,对应的能带宽度为3 eV以上,只能响应波长小于420 nm的紫外波段入射光谱。Dahal等[8]用MOCVD方法制备了多量子阱(MQW)型InGaN/GaN太阳电池,其填充因子为60%左右,开路电压大约为2 V,外量子效率为40%左右,太阳电池中InGaN层的In组分高达30%,对波长大于420 nm的入射光也有很好的响应。脉冲激光沉积(PLD)实验在20世纪60年代就已开始,当时利用发明不久的红宝石激光进行。但是一直到20世纪80年代末激光束外延成功后,它才得到迅速发展。1987年,美国贝尔实验室利用KrF激光器成功制备出高温超导薄膜YBa2Cu3O7-d[9]后,PLD在制备高温超导体、铁电体等复杂氧化物薄膜方面取得了极大的成功。随后它被用来制备超硬材料,生物兼容的耐磨镀层、高聚物、化合物半导体和纳米材料等,并取得了长足的进展。国内近年来也有一些研究机构(如中科院半导体研究所、南京大学、厦门大学等)在开展InGaN太阳电池的基础研究,研究工作包括太阳电池模拟计算、材料生长和物性表征等,且已有相关报道[10-14],但关于InGaN太阳电池实际制作方面的研究工作报道较少,只有最近厦门大学的Cai等[13]报道了他们在p-i-n型InGaN同质结太阳电池上的研究成果,指出降低缺陷密度是成功研制InGaN太阳电池的关键。【本研究切入点】脉冲激光沉积薄膜过程分为3个阶段:脉冲激光和靶材的相互作用产生等离子体,等离子体余辉在空间迅速膨胀,等离子体在基片表面的沉积成膜[15-17]。等离子体羽辉在膨胀过程中呈现椭球形状的原因是边界和初始条件决定的[18]。由于PLD制备过程中产生的等离子体具有明显的方向性,速率也不相同,导致在基片各处上形成的薄膜厚度并不均匀,而是存在一个厚度分布。因此,如何沉积出大面积的均匀薄膜已成为研究热点。【拟解决的关键问题】利用Origin软件,模拟PLD制备InGaN薄膜时膜的厚度分布,以及不同靶材-基片间夹角和靶基距对于膜厚分布的影响,找出其中的规律。
1 材料与方法 1.1 靶材与基片平行时膜厚的分布PLD是一种气相成膜方法,在实验上比较容易实现用聚焦的脉冲激光束,通过成膜腔的光学窗口烧蚀置于其中的靶材料,使部分靶材料蒸发并高速飞离靶面,形成羽状等离子体,其中的物质到达衬底后,在衬底表面迁移、凝聚、成核、最终生长成薄膜。PLD法制膜时,激光照射到靶材表面产生高温高压且成分结构复杂的等离子体羽辉,其空间分布形状可用高次余弦函数cosnθ来表示[19],θ为相对靶面法线的夹角,其典型值为5~10,随靶材而异。在此讨论夹角θ与膜厚d的关系,故将等离子体余辉简化为如图 1所示的阴影部分。在不同物质的蒸发过程中,蒸发源通常具有不同的形状,而点蒸发源是最简单的蒸发方式,也最容易进行数学描述和分析。由于激光照射部分的尺寸非常小,因此,为便于讨论,该过程可以简化为点蒸发源蒸发制膜的过程。假设靶材与基片完全平行,激光照射在靶材中心点,激光照射点的法线与基片相交点设为O点,由于以O为圆心的某一基片面上的圆,其圆弧上的所有点所处的环境(到O的距离、到靶材中心的距离)是一样的,所以任取基片上一条过O的直线来研究,即可得出基片上的膜厚分布特性。设O左侧为负,右侧为正,如图 2所示。

|
图 1 点蒸发源蒸发制膜的过程示意图 Fig.1 Diagram of the process of preparing the film by point evaporation source |
|
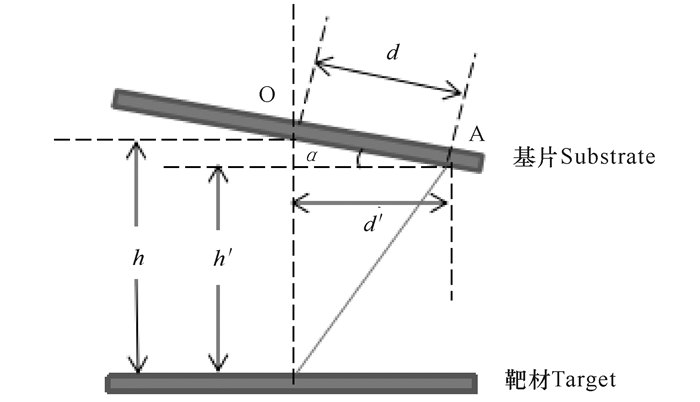
图 2 基片和靶材在PLD实际操作中存在一个偏转角α Fig.2 There is a deflection angle α between the substrate and the target in the actual PLD |
根据薄膜技术的相关原理可知,在基片任一面积元dAs上所沉积的薄膜物质的质量密度为
| $ \frac{{{\rm{d}}{M_s}}}{{{\rm{d}}{A_s}}} = \frac{{{M_e}\cos \theta }}{{\mathit{\Omega} {h^2}}}, $ | (1) |
其中,Me为空间角Ω内靶材的蒸发总质量,h为靶基距,θ为基片任一点偏离靶材法线的偏向角,设此时该点与基片上O点距离为d,该点薄膜厚度为t,薄膜密度为ρ,则有
| $ \rho t\frac{{{\rm{d}}{M_s}}}{{\rho td{A_s}}} = \frac{{{M_e}}}{{\mathit{\Omega} {h^2}}} \cdot \frac{h}{{\sqrt {{h^2} + {d^2}} }}, $ | (2) |
化简,得:
| $ t = \frac{{{M_e}}}{{\rho h\mathit{\Omega} \sqrt {{h^2} + {d^2}} }}, $ | (3) |
t即为基片上任一点处的膜厚函数。式中,Me/ρΩ为一个定值,其值与InGaN的特性有关。即薄膜的厚度t只与靶基距h以及该点与基片上O点的距离d相关。假设C为相对膜厚,即
| $ C = \frac{1}{{h\sqrt {{h^2} + {d^2}} }}。$ |
分别取h=3,4,5时相对膜厚C的分布,利用Origin软件绘制拟合曲线。当讨论整个基片面上的所有点的时候,各点与中心O点的距离没有正负之分,同样利用Origin软件绘制基片上距离中心O点距离为d的任一点的膜厚分布拟合曲线。
1.2 靶材与基片不平行时的膜厚分布在PLD制备InGaN薄膜的实际操作中,基片和靶材总是难以保证绝对平行,总会存在一个偏转角α,如图 2所示。
假设激光照射点处于靶材中心,过靶材中心垂直与靶材的直线与基片相交于点O,基片上O点左侧为正,右侧为负。取基片上任一面积元,则该面积元可近似作为平行于靶材时来处理,由几何关系不难看出,该面积元的等效靶基距h′和等效面积元到靶材垂线距离d′分别为h′=h-dsinα,d′=dcosα,代入前述公式(3)即得基片上任一点的膜厚公式为
| $ \begin{array}{l} t = \\ \frac{{{M_e}}}{{\rho \mathit{\Omega} \left( {h-d\sin \alpha } \right)\sqrt {{{\left( {h-d\sin \alpha } \right)}^2} + {d^2}{{\cos }^2}\alpha } }}。\end{array} $ | (5) |
同样地,式中Me/ρΩ为一个定值,则当靶材与基片存在一个偏转角时,其相对膜厚为
| $ C = \frac{1}{{\left( {h-d\sin \alpha } \right)\sqrt {{{\left( {h-d\sin \alpha } \right)}^2} + {d^2}{{\cos }^2}\alpha } }}。$ | (6) |
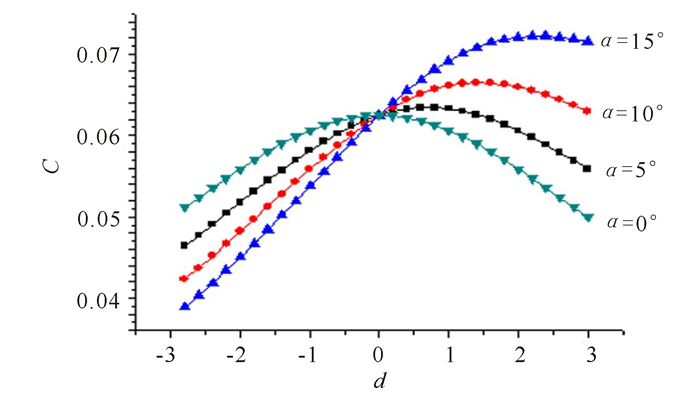
取h=4,α分别取0°,5°,10°,15°,然后利用Origin软件绘制相对膜厚C的分布曲线。
2 结果与分析 2.1 靶材与基片平行时膜厚的分布从图 3和图 4容易看出,距离基片中心点O越近,膜的厚度越大;靶基距越大,膜的厚度越小,膜厚分布越均匀。这说明,当基片与靶材处于平行状态时,基片上沉积形成的膜存在一个分布规律,靶材激光照射点处的法线与基片相交的点处形成的膜厚度最大,以该点为中心,基片两侧膜厚呈对称分布,且越远离O点,膜的厚度越小;增大靶基距,薄膜厚度均匀性得到提高,但与靶基距较小时相比,相同时间内沉积的薄膜厚度要低得多。

|
图 3 h=3,4,5时相对膜厚C的分布拟合曲线 Fig.3 The distribution likelihood curve of the relative thickness C when h=3, 4, 5 |

|
图 4 h=3,4,5时基片上距离中心O点距离为d的任一点的膜厚分布拟合曲线 Fig.4 The distribution likelihood curve of the film thickness when the distance is d from the point O |
分析图 5可知,当倾斜角为0°,即靶材平行于基片时,位于中心点O的膜厚最大,且基片左右两侧膜厚呈对称分布;当倾斜角不为0°,即靶材与基片存在一个倾斜角时,基片左右两侧膜厚不对称分布,靠近靶材一侧的薄膜厚度远大于远离靶材一侧的厚度,且倾斜角越大,两侧膜厚的差异越大;此时膜厚最大的点不位于中心点O,而是位于偏向靠近靶材的一侧,倾斜角越大,偏离越明显。
|
图 5 h=4,取α=0°,5°,10°,15°时相对膜厚C的分布拟合曲线 Fig.5 The distribution likelihood curve of the relative thickness C when α=0°, 5°, 10°, 15°, h=4 |
在PLD法制备InGaN薄膜的实际操作中,靶材和基片总会存在一个偏转角,本研究取任一无限小面积元近似作为平行靶材时的情况来分析,并使用Origin软件模拟PLD制备InGaN薄膜时此处各项等效参数,即可得到该处的膜厚。主要工作及结论如下:
1) 分析了PLD法制膜时靶材与基片存在倾斜角时的膜厚分布特性。当倾斜角为0°,即靶材平行于基片时,靶材激光照射点处的法线与基片相交的点处形成的膜厚度最大,以该点为中心,基片两侧膜厚呈对称分布,且越远离O点,膜的厚度越小;当倾斜角不为0°,即靶材与基片存在一个倾斜角时,基片左右两侧膜厚不对称分布,靠近靶材的一侧的薄膜厚度远大于远离靶材的一侧的厚度,且倾斜角越大,两侧膜厚的差异越大;此时膜厚最大的点不位于中心点O,而是位于偏向靠近靶材的一侧,倾斜角越大,偏离越明显。
2) 增大靶基距,薄膜厚度均匀性得到提高,但与靶基距较小时相比,相同时间内沉积的薄膜厚度要低得多。
当然, PLD法制备薄膜也有其缺点和局限性, 比如说烧蚀过程中容易产生肉眼可见的喷射粒子, 导致在薄膜中形成一些颗粒物,难以制备大面积的薄膜。如果烧蚀产物中粒子的动能过高, 可能会对已经形成的薄膜产生破坏,从而导致相关缺陷激光烧蚀产物在腔内的溅射对成膜腔的光学窗口有较严重的污染, 进而在一定程度上影响激光的有效利用[20]。其中,膜厚分布不均匀性是一大难题。改善PLD沉积薄膜的均匀性,一般从以下几个方面考虑:增大靶距、偏轴沉积(OFFSET)、激光束扫描、基片扫描、多光束沉积等[21]。在下一步的研究思路中,计划以分子动力学为基础,模拟PLD法沉积InGaN薄膜时等离子体余辉的各项等效参数,或是直接观测激光沉积的InGaN薄膜的等厚干涉条纹[22],探究膜厚的分布规律。InGaN薄膜材料的膜厚直接影响到太阳电池的性能,因此,研究PLD法沉积InGaN薄膜时膜厚的分布规律,以便于能够降低薄膜的缺陷密度,改善薄膜的均匀性,具有重要意义。
| [1] |
何江. 日本民用住宅太阳能发电新技术[J]. 广西科学院学报, 1996, 12(1): 1-3. HE J. New solar energy technology on housing photovoltaic system in Japan[J]. Journal of Guangxi Academy of Sciences, 1996, 12(1): 1-3. |
| [2] |
李福宾, 林硕, 李建功, 等. GaN肖特基紫外探测器的电流输运研究[J]. 广西科学, 2009, 16(2): 158-160. LI F B, LIN S, LI J G, et al. Current transport of GaN Schottky UV detectors[J]. Guangxi Sciences, 2009, 16(2): 158-160. |
| [3] |
侯彩霞, 郑新和, 彭铭曾, 等. InGaN/GaN多量子阱电池的垒层结构优化及其光学特控[J]. 半导体光电, 2017, 38(5): 709-713. HOU C X, ZHENG X H, PENG M Z, et al. Barrier optimization and optical property control of InGaN/GaN Multiple Quantum Wells[J]. Semiconductor Optoelectronics, 2017, 38(5): 709-713. |
| [4] |
周明斌, 李振荣, 范世马岂, 等. GaN体单晶生长研究进展[J]. 中国照明电器, 2017, 9: 7-14. ZHOU M B, LI Z R, FENSHI M Q, et al. Progress of the growth of GaN single crystals[J]. China Light & Lighting, 2017, 9: 7-14. |
| [5] |
赖萌华, 张保平. InGaN/GaN量子阱太阳能电池研究进展[J]. 厦门大学学报, 2015, 54(5): 652-664. LAI M H, ZHANG B P. Research process of InGaN/GaN multiple-quantum-well solar cells[J]. Journal of Guangxi Academy of Sciences, 2015, 54(5): 652-664. |
| [6] |
JANI O, FERGUSON I, HONSBERG C B, et al. Design and characterization of GaN/InGaN solar cells[J]. Appl Phys Lett, 2007, 91: 132117. DOI:10.1063/1.2793180 |
| [7] |
NEUFELD C J, TOLEDO N G, CRUZ S C, et al. High quantum efficiency InGaN/GaN solar cells with 2.95 eV band gap[J]. Appl Phys Lett, 2008, 93: 143502. DOI:10.1063/1.2988894 |
| [8] |
DAHAL R, PANTHA B, LI J, et al. InGaN/GaN multiple quantum well solar cells with long operating wavelengths[J]. Appl Phys Lett, 2009, 94: 063505. DOI:10.1063/1.3081123 |
| [9] |
DIJKKAMP D, VENKATEASAN T, WU X D, et al. Preparation of Y-Ba-Cu oxide superconductor thin films using pulsed laser evaporation from high Tc bulk material[J]. Appl Phys Lett, 1987, 51: 619-621. DOI:10.1063/1.98366 |
| [10] |
ZHANG X B, WANG X L, XIAO H L, et al. Simulation of In0.65Ga0.35N single-junction solar cell[J]. Journal of Physics D:Applied Physics, 2007, 40(23): 7335-7338. DOI:10.1088/0022-3727/40/23/013 |
| [11] |
SHEN X M, LIN S, LI F B, et al. Simulation of the InGaN-based tandem solar cells[J]. Proc of SPIE, 2008, 7045(1): 70450E. |
| [12] |
LI J G, LI F B, LIN S, et al. Theoretical study on InxGa1-xN/Si hetero-junction solar cells[J]. Proc of SPIE, 2009, 7409: 740910. DOI:10.1117/12.826088 |
| [13] |
CAI X M, ZENG S W, ZHANG B P. Fabrication and characterization of InGaN p-i-n homojunction solar cell[J]. Appl Phys Lett, 2009, 95: 173504. DOI:10.1063/1.3254215 |
| [14] |
KANG J H, EBAID M, LEE J K, et al. Optical study of phase-separated thick InGaN layers grown on a compliant substrate[J]. Applied Physics A, 2015, 121(2): 765-771. DOI:10.1007/s00339-015-9478-4 |
| [15] |
陈中军, 张端明, 李智华, 等. 脉冲激光沉积KTN薄膜动力学过程模拟[J]. 华中理工大学学报, 2000, 28(5): 92-94. CHEN Z J, ZHANG D M, LI Z H, et al. Simulation of the dynamics process of pulsed laser deposition of KTN thin film[J]. Journal of Huazhong University of Science and Technology, 2000, 28(5): 92-94. |
| [16] |
宋宁宁. InGaZnO透明导电薄膜的PLD制备及其性能表征[D]. 哈尔滨: 哈尔滨工业大学, 2012. SONG N N. Characterization of InGaZnO transparent conductive thin films by PLD method[D]. Harbin: Harbin Institute of Technology, 2012. |
| [17] |
高国棉, 陈长乐, 陈钊, 等. 脉冲激光沉积(PLD)的研究动态与新发展[J]. 材料导报, 2005, 19(2): 69-71. GAO G M, CHEN C L, CHEN Z, et al. Review of pulsed laser deposition technology[J]. Materials Review, 2005, 19(2): 69-71. |
| [18] |
关丽. 脉冲激光沉积技术中等离子体演化及薄膜生长的模拟研究[D]. 湖北: 华中科技大学, 2006. GUAN L. Study on plasma evolution and film growth in pulsed laser deposition[D]. Hubei: Huazhong University of Science and Technology, 2006. http://www.doc88.com/p-1971581219096.html |
| [19] |
江辉明, 叶志清, 曾明生. 脉冲激光沉积(PLD)机理分析及其应用[J]. 江西师范大学学报, 2005, 29(1): 53-57. JIANG H M, YE Z Q, ZENG M S. Application and mechanism analysis of pulsed laser deposition[J]. Journal of Jiangxi Normal University, 2005, 29(1): 53-57. |
| [20] |
卢意飞. GaN及GaN基薄膜的制备、表征和特性研究[D]. 上海: 复旦大学, 2008. LU Y F. Preparation, characterization and properties of GaN and GaN based films[D]. Shanghai: Fudan University, 2008. |
| [21] |
张磊, 王秀凤, 林晓东. 脉冲激光沉积类金刚石薄膜的厚度均匀性建模[J]. 西南科技大学学报, 2007, 22(4): 14-19. ZHANG L, WANG X F, LIN X D. The thickness uniformity modeling for DLC films obtained by PLD[J]. Journal of Southwest University of Science and Technology, 2007, 22(4): 14-19. |
| [22] |
皇甫国庆. 脉冲激光沉积BST铁电薄膜的厚度分布[J]. 陕西师范大学学报:自然科学版, 2003, 31(3): 55-58. HUANGFU G Q. Thickness distribution of BST ferroelectric film deposited by pulsed laser[J]. Journal of Shaanxi Normal University:Natural Science Edition, 2003, 31(3): 55-58. |
 2017, Vol. 24
2017, Vol. 24 


