Distributed Sampled-data Synchronization for a Class of Complex Dynamical Networks with Coupling Delays
0 引言 【研究意义】随着数字控制技术逐步取代模拟控制技术,采样控制在工程领域得到了越来越广泛的应用.采样控制的主要特征是利用系统在一系列离散时刻的采样信息,对系统施加反馈控制.这表明,在采样控制框架下,需要传输的信息量大大减少,从而减少了带宽的使用,并增加了控制器的鲁棒性.基于采样控制这些显著优点,不少学者应用采样控制策略研究非线性系统的状态估计与同步控制问题. 【前人研究进展】 Chen等[1]研究了带有非均匀采样的Lipschitz非线性系统的观测器设计问题.通过构造一个时间依赖的Lyapunov函数来捕捉误差系统的动态特征,建立了一个保守性较小的稳定性判据.Zhang等[2]讨论了混合时滞神经网络的采样同步问题.基于Lyapunov泛函方法,输入时滞和改进的自由权重矩阵方法,推导出了时滞神经网络指数同步判据.Lu等[3]和Chen等[4]通过采样反馈控制研究了混沌Lur’e系统的主从同步问题,利用自由权重矩阵方法得到了混沌Lur’e系统全局渐近同步的充分条件.近年来,基于离散时刻的采样信息,建立复杂动态网络(Complex Dynamical Networks,CDNs)同步准则,也取得了一些结果.基于采样信息的同步控制策略可以分为采样控制策略和脉冲控制策略.Chen等[5-6]分别基于分散脉冲控制策略和分布脉冲控制策略研究了CDNs的全局同步问题.Li等[7]研究了一类具有耦合时滞的CDNs的采样同步控制问题,通过把采样周期转换成一个有界的时变时滞,从而把采样同步问题转化为一个具有多时滞的微分等式的稳定性问题.通过构造一个Lyapunov泛函和利用Jensen不等式推导出了具有多时滞的微分等式的指数稳定的充分条件.Shen等[8]研究了CDNs的随机采样同步问题,采样周期在两个不同的值之间依概率切换.Lee等[9]基于时滞采样控制策略研究了具有时变耦合时滞CDNs的同步问题.基于扩展的Wirtinger不等式,构造了不连续的Lyapunov函数,并以线性矩阵不等式(LMIs)的形式给出了CDNs的稳定性判据.Wu等[10]通过采样控制策略研究了一类具有耦合时变时滞的CDNs的指数同步问题,并建立了CDNs指数同步的判据,值得注意的是,这里的采样周期是时变有界的.Jia等[11]研究了多智能体网络的采样同步问题.对于不同拓扑结构连接方法的多智能体网络的采样周期上界的最小值进行了分析.Wang等[12]基于时间依赖的Lyapunov函数方法研究了连续动态网络的采样同步问题,以LMIs的形式给出了连续动态网络的同步判据,并对采样周期上界的最大值进行估计.上述文献所采用的分析方法都是时不变的Lyapunov函数方法,并不能充分体现采样控制器对受控系统的影响.为此,一些研究者通过构造时间依赖的Lyapunov函数来考虑CDNs的状态同步问题.Wang等[13]研究了一类具有耦合时变时滞和随机耦合力的CDNs的采样同步问题.通过构造不连续的Lyapunov函数建立了时滞相关的均方同步判据,基于所建立的同步判据对系统设计了采样控制器.
文献[11]所考虑的线性多智能体网络具有如下形式:
|
$
{{\dot x}_i}\left( t \right) = A{x_i}\left( t \right) + {u_i}\left( t \right),i \in \mathscr{N},
$
|
其中xi(t)是第i个节点的状态变量,$\mathscr{N}$为节点集,ui(t)是第i个节点的分布采样控制输入,形式如下:
|
$
{u_i}\left( t \right) = \alpha \sum\limits_{j \in {N_i}} {{g_{ij}}C\left( {{x_j}\left( {{t_k}} \right) - {x_i}\left( {{t_k}} \right)} \right)} ,t \in \left[ {{t_k},{t_{k + 1}}} \right],k \in \mathbb{N},
$
|
(1) |
gij为第j个节点与第i个节点间的耦合控制力,{tk}是采样时间序列,C∈ℝn×n表示内耦合矩阵,α∈ℝ+是耦合力,$\mathbb{N}$为非负整数集,Ni为所有与第i个节点相邻的节点构成的节点子集.
但是在实际的应用当中,很多系统模型都不是线性的.所以,文献[11]所考虑的模型在实际应用中具有一定的局限性.为此,文献[12]考虑了如下形式的多智能体网络:
|
$
{{\dot x}_i}\left( t \right) = A{x_i}\left( t \right) + f\left( {{x_i}\left( t \right)} \right) + {u_i}\left( t \right),i \in \mathscr{N},
$
|
其中xi(t)是第i个节点的状态变量,f(xi(t))为连续的非线性向量函数,ui(t)是第i个节点的控制输入,且其形式为式(1)所示.显然,相比文献[11],文献[12]所考虑的模型更具广泛性.Wu等[14]考虑了如下具有耦合时变时滞的CDNs:
|
$
\begin{array}{l}
{{\dot x}_i}\left( t \right) = f\left( {{x_i}\left( t \right)} \right) + c\sum\limits_{j = 1}^N {{G_{ij}}A{x_j}\left( {t - \tau \left( t \right)} \right)} + \\
{u_i}\left( t \right),i \in \mathscr{N},
\end{array}
$
|
其中xi(t)是第i个节点的状态变量,f(xi(t))为连续的非线性向量函数,Gij表示为第j个节点与第i个节点的耦合控制力,c∈ℝ+是耦合力,ui(t)为控制输入.但该文献所考虑的分散采样控制器为
|
$
{u_i}\left( t \right) = {K_i}\left( {{x_i}\left( {{t_k}} \right) - s\left( t \right)} \right),t \in \left[ {{t_k},{t_{k + 1}}} \right),k \in \mathbb{N},
$
|
其中s(t)∈ℝn是孤立节点ṡ(t)=f(s(t))的状态轨线,Ki是状态反馈控制器的增益矩阵.分散采样控制策略忽略了其相邻节点的状态信息,所以不适合于具有强耦合力的CDNs,更适合于弱耦合力的CDNs.而在文献[11]和文献[12]中没有考虑到分布采样控制器的设计问题. 【本研究切入点】 在实际应用中,控制器设计的优劣直接影响到受控系统的应能.因此,对具有耦合时变时滞的CDNs,如何设计优化分布采样同步控制器,仍然是亟待解决的问题. 【拟解决的关键问题】 针对具有耦合时变时滞CDNs,研究具有最小耦合力的分布采样同步控制器的设计问题.基于时间依赖的Lyapunov函数的方法和凸组合技术,运用Jensen不等式处理积分项,建立同步误差系统指数稳定性的判据,在此基础上,给出迭代算法,用来设计具有最小耦合力的分布采样同步控制器.
1 问题描述 考虑具有N个线性时滞耦合CDNs,每个节点是一个n维动态系统,其状态方程如下:
|
$
\begin{array}{l}
{{\dot x}_i}\left( t \right) = A{x_i}\left( t \right) + f\left( {t,{x_i}\left( t \right)} \right) + \sum\limits_{j = 1}^N {{b_{ij}}\mathit{\Gamma }{\mathit{x}_j}\left( {t - } \right.} \\
\left. {\tau \left( t \right)} \right) + {u_i}\left( t \right),i \in \mathscr{N},
\end{array}
$
|
(2) |
其中N是节点个数,xi(t)=(xi1, xi2, …, xin)T∈ℝn是第i个节点的状态,ui(t)是第i个节点的控制输入,f:ℝ+×ℝn→ℝn是一个连续的向量函数,满足f(t, 0)=0,τ(t)是时变耦合时滞.A∈ℝn×n为已知的常系数矩阵,Γ∈ℝn×n为内耦合矩阵,B$\buildrel \Delta \over = $(bij)N×N是耦合配置矩阵且满足耦合条件:bii=$-\sum\limits_{j = 1, j \ne i}^N {{b_{ij}}} $,当i≠j时, bij>0, ∀i, j∈$\mathscr{N}$.如果第i个节点与第j个节点相耦合,则bij>0, i≠j,否则,bij=0.另外,对于非线性向量函数f(t, x)与时变耦合时滞τ(t),分别满足如下假设:
(H1)存在具有合适维数的矩阵L使得下列不等式成立:
|
$
\begin{gathered}
\left\| {f\left( {t,x} \right) - f\left( {t,y} \right)} \right\| \leqslant \left\| {L\left( {x - y} \right)} \right\|,\forall t \in \hfill \\
{\mathbb{R}^ + },\forall x,y \in {\mathbb{R}^n}. \hfill \\
\end{gathered}
$
|
(H2)存在标量τ>0和δ < 1,使得时变耦合时滞τ(t)满足0≤τ(t)≤τ, $\dot \tau $(t)≤δ.
考虑如下形式的分布采样同步控制器:
|
$
\begin{gathered}
{u_i}\left( t \right) = \sum\limits_{j \in {N_i}} {{\nu _{ij}}\mathit{\Gamma }\left( {{x_j}\left( {{t_k}} \right) - {x_i}\left( {{t_k}} \right)} \right)} ,t \in \left[ {{t_k},{t_{k + 1}}} \right), \hfill \\
k \in \mathbb{N}, \hfill \\
\end{gathered}
$
|
(3) |
其中νij是第j个节点与第i个节点的耦合力,{tk, k∈$\mathbb{N}$ }∈S(h)是采样时间序列,这里S(h)={{tk}; 0 < tk+1-tk≤h, k∈$\mathbb{N}$ },h表示采样区间的上界.
注1 式(3)所考虑的分布采样同步控制器不要求采样区间是周期的,相比于周期采样同步控制器,变周期采样同步控制器具有更大的灵活性和鲁棒性.
将(3)代入到(2),得到闭环系统:
|
$
\begin{gathered}
{{\dot x}_i}\left( t \right) = A{x_i}\left( t \right) + f\left( {t,{x_i}\left( t \right)} \right) + \sum\limits_{j = 1}^N {{b_{ij}}\mathit{\Gamma }{\mathit{x}_j}\left( {t - } \right.} \hfill \\
\left. {\tau \left( t \right)} \right) + \sum\limits_{j \in {N_i}} {{\nu _{ij}}\mathit{\Gamma }\left( {{x_j}\left( {{t_k}} \right) - {x_i}\left( {{t_k}} \right)} \right)} ,t \in \left[ {{t_k},{t_{k + 1}}} \right), \hfill \\
k \in \mathbb{N}. \hfill \\
\end{gathered}
$
|
(4) |
定义νii=$-\sum\limits_{j = 1, j \ne i}^N {{\nu _{ij}}} $,如果j∉$\mathscr{N}$i, j≠i,则νij=0.令Δ=(νij)N×N.根据Kronecker积的性质,采样受控CDNs(4)可以改写为
|
$
\begin{gathered}
\dot x\left( t \right) = \left( {{I_N} \otimes A} \right)x\left( t \right) + f\left( {t,x\left( t \right)} \right) + \hfill \\
\left( {B \otimes \mathit{\Gamma }} \right)x\left( {t - \tau \left( t \right)} \right) + \left( {\Delta \otimes \mathit{\Gamma }} \right)x\left( {{t_k}} \right),t \in \left[ {{t_k},{t_{k + 1}}} \right), \hfill \\
k \in \mathbb{N}, \hfill \\
\end{gathered}
$
|
(5) |
其中x=col(x1, …, xN), f(t, x)=col(f(t, x1), …, f(t, xN)).
定义同步误差为ei(t)=xi(t)-xi+1(t), i∈$\mathscr{N}$-{N}.令e=col(e1, e2, …, eN-1),易得到下列等式:
|
$
\begin{array}{l}
GM = {I_{N - 1}},B = BMG,\Delta = \Delta MG,\left( {G \otimes {I_N}} \right)\\
x = e,
\end{array}
$
|
(6) |
且有
|
$
\begin{array}{l}
\left( {G \otimes {I_N}} \right)\left( {{I_N} \otimes A} \right) = G \otimes A = \\
\left( {{I_{N - 1}} \otimes A} \right)\left( {G \otimes {I_n}} \right)
\end{array}
$
|
|
$
\begin{array}{l}
\left( {G \otimes {I_n}} \right)\left( {B \otimes \mathit{\Gamma }} \right) = GB \otimes \mathit{\Gamma } = \left( {GBMG} \right) \otimes \mathit{\Gamma } = \\
\left( {\left( {GBM} \right) \otimes \mathit{\Gamma }} \right)\left( {G \otimes {I_n}} \right)
\end{array}
$
|
|
$
\begin{array}{l}
\left( {G \otimes {I_n}} \right)\left( {\Delta \otimes \mathit{\Gamma }} \right) = \left( {G\Delta } \right) \otimes \mathit{\Gamma } = \\
\left( {G\Delta MG} \right) \otimes \mathit{\Gamma } = \left. {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right)\left( {G \otimes {I_n}} \right),
\end{array}
$
|
其中
|
$
G = \left[ {\begin{array}{*{20}{c}}
1&{ - 1}&0& \cdots &0 \\
0&1&{ - 1}& \cdots &0 \\
\vdots&\vdots&\vdots&\vdots&\vdots \\
0&0& \cdots &1&{ - 1}
\end{array}} \right] \in {\mathbb{R}^{\left( {N - 1} \right) \times N}},
$
|
|
$
M = \left[ {\begin{array}{*{20}{c}}
1&1& \cdots &1 \\
0&1& \cdots &1 \\
\vdots&\vdots&\vdots&\vdots \\
0&0& \cdots &1 \\
0&0& \cdots &0
\end{array}} \right] \in {\mathbb{R}^{N \times \left( {N - 1} \right)}}.
$
|
对式(5)左乘GⓧIn,通过式(6)可以得到同步误差系统:
|
$
\begin{gathered}
\dot e\left( t \right) = \left( {{I_{N - 1}} \otimes A} \right)e\left( t \right) + \bar f\left( {t,x\left( t \right)} \right) + \hfill \\
\left( {GBM \otimes \mathit{\Gamma }} \right)e\left( {t - \tau \left( t \right)} \right) + \left( {G\Delta M \otimes \mathit{\Gamma }} \right)e\left( {{t_k}} \right),t \in \left[ {{t_k},} \right. \hfill \\
\left. {{t_{k + 1}}} \right),k \in \mathbb{N}, \hfill \\
\end{gathered}
$
|
(7) |
其中f(t, x(t))=col(f(t, x1)-f(t, x2), …, f(t, xN-1)-f(t, xN)).
对于给定的采样时间序列S(h),引入如下分段函数:
|
$
{\rho _1}\left( t \right) = t - {t_k},{\rho _2}\left( t \right) = {t_{k + 1}} - t,t \in \left[ {{t_k},{t_{k + 1}}} \right).
$
|
则对于采样时间序列{tk, k∈$\mathbb{N}$ }∈S(h),如下不等式成立:
|
$
0 < {\rho _1}\left( t \right) + {\rho _2}\left( t \right) \le h,0 \le {\rho _1}\left( t \right) \le h.
$
|
(8) |
根据上面所引入的分段函数,误差动态系统(7)改写为如下变时滞系统形式:
|
$
\begin{gathered}
\dot e\left( t \right) = \left( {{I_{N - 1}} \otimes A} \right)e\left( t \right) + \bar f\left( {t,x\left( t \right)} \right) + \hfill \\
\left( {GBM \otimes \mathit{\Gamma }} \right)e\left( {t - \tau \left( t \right)} \right) + \left( {G\Delta M \otimes \mathit{\Gamma }} \right)e\left( {t - {\rho _1}\left( t \right)} \right), \hfill \\
t \in \left[ {{t_k},{t_{k + 1}}} \right),k \in \mathbb{N}. \hfill \\
\end{gathered}
$
|
(9) |
注2 在同步误差系统(9)中,把(t-tk)看作是系统的一个时变时滞ρ1(t),其上界为h,导数满足${\dot \rho _1}\left( t \right) = 1$.
下面给出本文所需的定义与引理.
定义1 设e(t, t0, ϕ)是系统(9)过(t0, ϕ)的解.给定一类采样时间序列S(h),如果存在正标量c和K,对任意的初始条件和{tk}∈S(h),下列不等式成立:
|
$
\left\| {e\left( {t,{t_0},\phi } \right)} \right\| \le K{e^{ - c\left( {t - {t_0}} \right)}}{\left\| \phi \right\|_{\bar \tau }},t > 0.
$
|
则称系统(9)的零解关于S(h)是一致全局指数稳定(UGES)的.
引理1(文献[15]) 给定标量a, b满足b>0, $a >-2\sqrt b $.令标量$c = \frac{1}{2}\sqrt {\left| {4b-{a^{^2}}} \right|} $.定义函数ν具有如下形式:
|
$
\nu = \nu \left( {a,b} \right) \buildrel \Delta \over = \left\{ \begin{array}{l}
\frac{1}{c}\arctan h\frac{{2c}}{a},a > 2\sqrt b ;\\
\frac{2}{a},a = 2\sqrt b ;\\
\frac{1}{c}\arctan \frac{{2c}}{a},0 < a < 2\sqrt b ;\\
\frac{\pi }{{2c}}, - 2\sqrt b < a \le 0.
\end{array} \right.
$
|
令α, T和σ为正常数,ε∈(0, T], Ψ(t, Ψ0)为如下初值问题的解:
|
$
\left\{ \begin{array}{l}
\mathit{\dot \Psi } = - \frac{\nu }{{\varepsilon + \sigma }}\left( {{\mathit{\Psi }^2} + a\mathit{\Psi } + b} \right),t \ge \alpha \\
\mathit{\Psi }\left( \alpha \right) = {\mathit{\Psi }_0} > 0
\end{array} \right.,
$
|
(10) |
则存在一个仅依赖α, T, a, b的正常数ρ和初值Ψ*∈(0, ρ),使得系统(10)的解Ψ(t)=(t, Ψ0*)具有如下性质:
|
$
\mathit{\Psi }\left( {\alpha + \varepsilon } \right) = 0,\mathit{\dot \Psi }\left( t \right) < 0,t \in \left[ {\alpha ,\alpha + \varepsilon } \right].
$
|
引理2(文献[16]) (Jensen不等式)对任意给定的正定矩阵Q和参数γ1,γ2,其中γ1, γ2满足γ1 < γ2.若存在向量函数x:[γ1, γ2]→ℝn使得下面的积分有意义,则积分不等式成立:
|
$
\begin{array}{l}
\int_{{\gamma _1}}^{{\gamma _2}} {{x^{\rm{T}}}\left( s \right)Qx\left( s \right){\rm{d}}s} \ge \\
\frac{1}{{{\gamma _2} - {\gamma _1}}}\left( {\int_{{\gamma _1}}^{{\gamma _2}} {{x^{\rm{T}}}\left( s \right){\rm{d}}s} } \right)Q\left( {\int_{{\gamma _1}}^{{\gamma _2}} {x\left( s \right){\rm{d}}s} } \right).
\end{array}
$
|
引理3(文献[17]) 对任意矩阵$\left[{\begin{array}{*{20}{c}}
{{M_1}}&S\\
*&{{M_2}}
\end{array}} \right]$≥0,标量τ>0,如果存在τ(t)满足0≤τ(t)≤τ,且向量函数ė(·):[-τ, 0]→ℝn使得下面的积分有意义,则积分不等式成立:
|
$
\begin{array}{l}
- \tau \int_{t - \tau \left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){M_1}e\left( s \right){\rm{d}}s} - \\
\tau \int_{t - \tau }^{t - \tau \left( t \right)} {{{\dot e}^{\rm{T}}}\left( s \right){M_2}e\left( s \right){\rm{d}}s} \le {\eta ^{\rm{T}}}\left( t \right)\mathit{\Lambda }\eta \left( t \right),
\end{array}
$
|
其中ηT(t)=(eT(t), eT(t-τ(t)), eT(t-τ)),
|
$
\mathit{\Lambda } = \left[ {\begin{array}{*{20}{c}}
{ - {M_1}}&{{M_1} - S}&S\\
* &{ - {M_1} - {M_2} + S + {S^{\rm{T}}}}&{{M_2} - S}\\
*&* &{ - {M_2}}
\end{array}} \right].
$
|
2 稳定性分析 为了捕捉采样对同步误差系统(7)的动力学行为的影响,构造与采样时间序列相关的时间依赖的Lyapunov函数来分析同步误差系统(7)的稳定性.
根据引理1可知,对于给定的采样时间序列{tk}∈S(h),任意给定的标量a, b满足b>0, $a >-2\sqrt b $和任意给定的正标量ε1,存在仅依赖于a, b, h, ε1的标量ρ>0,使得初值Ψ0k∈(0, ρ),Ψk(t)=Ψk(t, Ψ0k)是满足如下初值问题的唯一解:
|
$
\left\{ \begin{array}{l}
\mathit{\dot \Psi } = - \frac{\nu }{{{\varepsilon _1} + {h_k}}}\left( {{\mathit{\Psi }^2}\mathit{ + a\Psi + b}} \right),t \ge {t_k}\\
\mathit{\Psi }\left( \alpha \right) = {\phi _{0k}} > 0
\end{array} \right.,
$
|
其中hk表示为第k个采区间的上界,k∈$\mathbb{N}$.则Ψk具有以下性质:
|
$
{\mathit{\Psi }_k}\left( {{t_{k + 1}}} \right) = 0,{{\mathit{\dot \Psi }}_k}\left( t \right) < 0,t \in \left[ {{t_k},{t_{k + 1}}} \right].
$
|
(11) |
定义分段可微函数Ψ:[t0, ∞)→ℝ+满足:
|
$
\begin{gathered}
\mathit{\Psi }\left( t \right) = {\mathit{\Psi }_k}\left( t \right),\mathit{\Psi }\left( {{t_k}} \right) \triangleq \mathit{\Psi }\left( {t_k^ + } \right) = {\mathit{\Psi }_k}\left( {{t_k}} \right),t \in \hfill \\
\left( {{t_k},{t_{k + 1}}} \right),k \in \mathbb{N}. \hfill \\
\end{gathered}
$
|
(12) |
根据式(11)和式(12)可得
|
$
\begin{gathered}
\mathit{\Psi }\left( {t_k^ - } \right) = 0,0 \leqslant \mathit{\Psi }\left( t \right) \leqslant \rho ,t \geqslant {t_0},k \in \mathbb{N}, \hfill \\
\mathit{\dot \Psi } \leqslant - \frac{\nu }{{h + {\varepsilon _1}}}\left( {{\mathit{\Psi }^2}\mathit{ + a\Psi + b}} \right) < 0,t \ne {t_k},k \in \mathbb{N}. \hfill \\
\end{gathered}
$
|
(13) |
构造时间依赖的Lyapunov函数:
|
$
V\left( t \right) \buildrel \Delta \over = V\left( {t,e\left( t \right)} \right) = \sum\limits_{i = 1}^8 {{V_i}\left( {t,e\left( t \right)} \right)} ,
$
|
(14) |
Vi(t, e(t))分别表示如下:
|
$
{V_1}\left( {t,e\left( t \right)} \right) = {e^{\rm{T}}}\left( t \right){P_1}e\left( t \right),
$
|
|
$
\begin{array}{l}
{V_2}\left( {t,e\left( t \right)} \right) = {\rho _2}\left( t \right)\left[ {{{\tilde e}^{\rm{T}}}\left( t \right){P_2}\tilde e\left( t \right) + 2\left( {e\left( t \right) - } \right.} \right.\\
\left. {\left. {\tilde e\left( t \right)} \right){P_3}\tilde e\left( t \right)} \right],
\end{array}
$
|
|
$
\begin{array}{l}
{V_3}\left( {t,e\left( t \right)} \right) = \mathit{\Psi }\left( t \right){e^{\rm{T}}}\left( t \right)\left[ {{\rho _2}\left( t \right){P_4} + \left( {h - } \right.} \right.\\
\left. {\left. {{\rho _2}\left( t \right)} \right){P_5}} \right]\tilde e\left( t \right),
\end{array}
$
|
|
$
{V_4}\left( {t,e\left( t \right)} \right) = {\rho _2}\left( t \right)\int_{t - {\rho _1}\left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_1}\dot e\left( s \right){\rm{d}}s} ,
$
|
|
$
{V_5}\left( {t,e\left( t \right)} \right) = \int_{t - \tau \left( t \right)}^t {{e^{\rm{T}}}\left( s \right){Q_2}e\left( s \right){\rm{d}}s} ,
$
|
|
$
{V_6}\left( {t,e\left( t \right)} \right) = \int_{t - \tau }^t {{e^{\rm{T}}}\left( s \right){Q_2}e\left( s \right){\rm{d}}s} ,
$
|
|
$
{V_7}\left( {t,e\left( t \right)} \right) = \tau \int_{ - \tau }^0 {\int_{t + \theta }^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_4}\dot e\left( s \right){\rm{d}}s{\rm{d}}\theta } } ,
$
|
|
$
{V_8}\left( {t,e\left( t \right)} \right) = \tau \int_{ - \tau \left( t \right)}^0 {\int_{t + \theta }^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_5}\dot e\left( s \right){\rm{d}}s{\rm{d}}\theta } } ,
$
|
其中ẽ(t)=e(t)-e(t-ρ1(t)),矩阵P1>0, P4>0, P5>0, Qi>0, i=1, …, 5, P2T=P2.
注3 由于Ψ(t), ρ1(t), ρ2(t)在(tk, tk+1)内是连续的,所以本文所构造的时间依赖的Lyapunov函数V(t)在[t0-τ, +∞)连续,且在$\bigcup\limits_{k = 0}^\infty {\left( {{t_k}, {t_{k + 1}}} \right)} $上可微.
根据式(14)所构造的时间依赖的Lyapunov函数来分析同步误差系统(9)的稳定性.为了表述方便,引入以下符号:
|
$
{\mathscr{I}_1} = \left[ {{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 5n\left( {N - 1} \right)}}} \right],
$
|
|
$
{\mathscr{I}_2} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 4n\left( {N - 1} \right)}}} \right],
$
|
|
$
{\mathscr{I}_3} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 3n\left( {N - 1} \right)}}} \right],
$
|
|
$
\begin{array}{l}
{\mathscr{I}_{13}} = \left[ {{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}, - {\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},} \right.\\
\left. {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 3n\left( {N - 1} \right)}}} \right],
\end{array}
$
|
|
$
\begin{array}{l}
\mathscr{A} = \left[ {\left( {{\mathit{\boldsymbol{I}}_{\left( {N - 1} \right)}} \otimes \mathit{\boldsymbol{A}}} \right), - {\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}},} \right.\\
\left. {\left( {GBM \otimes \mathit{\Gamma }} \right),{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}}} \right],
\end{array}
$
|
|
$
\begin{array}{l}
{\xi ^{\rm{T}}}\left( t \right) = \left[ {{e^{\rm{T}}}\left( t \right),{{\dot e}^{\rm{T}}}\left( t \right),{{\tilde e}^{\rm{T}}}\left( t \right),{e^{\rm{T}}}\left( {t - \tau \left( t \right)} \right),{e^{\rm{T}}}\left( {t - } \right.} \right.\\
\left. {\left. \tau \right),{{\bar f}^{\rm{T}}}\left( {t,x\left( t \right)} \right)} \right].
\end{array}
$
|
可以得到下面的式子:
|
$
\begin{array}{l}
e\left( t \right) = {\mathscr{I}_1}\xi \left( t \right),\dot e\left( t \right) = {\mathscr{I}_2}\xi \left( t \right),\tilde e\left( t \right) = {\mathscr{I}_3}\xi \left( t \right),e\left( {t - } \right.\\
\left. {\tau \left( t \right)} \right) = {\mathscr{I}_4}\xi \left( t \right),
\end{array}
$
|
|
$
\begin{array}{l}
e\left( {t - \tau } \right) = {\mathscr{I}_5}\xi \left( t \right),{{\bar f}^{\rm{T}}}\left( {t,x\left( t \right)} \right) = {\mathscr{I}_6}\xi \left( t \right),e\left( {t - } \right.\\
\left. {{\rho _1}\left( t \right)} \right) = {\mathscr{I}_{13}}\xi \left( t \right).
\end{array}
$
|
定理1 考虑同步误差系统(9),假设(H1)和(H2)成立.给定N×N维增益矩阵Δ,采样时间序列S(h),若存在标量βj>0, j=1, 2, 和标量a, b满足b>0, $a >-2\sqrt b $,n(N-1)×n(N-1)维矩阵P1>0, P4>0, P5>0, Qi>0, P2T=P2, P3, S, F11, F12, F21, F22, i=1, …, 5, 和6n(N-1)×n(N-1)维矩阵M1,使得下列矩阵不等式成立:
|
$
\left[ {\begin{array}{*{20}{c}}
{{Q_4} + \left( {1 - \delta } \right){Q_5}}&S\\
* &{{Q_4}}
\end{array}} \right] \ge 0,
$
|
(15) |
|
$
\left[ {\begin{array}{*{20}{c}}
{{P_1}}&{h{P_3}}\\
* &{{Q_1} + h\left( {{P_2} - {P_3} - P_3^{\rm{T}}} \right)}
\end{array}} \right] > 0,
$
|
(16) |
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\Omega }_1} + {\mathit{\Omega }_2}}&{{\mathit{\Omega }_{12}}}\\
* &{ - \nu {P_4}}
\end{array}} \right] < 0,\\
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\Omega }_1} + {\mathit{\Omega }_3}}&{{\mathit{\Omega }_{22}}}&{h{M_1}}\\
* &{ - \nu {P_5}}&0\\
*&* &{ - h{Q_1}}
\end{array}} \right] < 0,
\end{array}
$
|
(17) |
其中
|
$
\begin{array}{l}
{\mathit{\Omega }_1} = \mathscr{I}_1^{\rm{T}}\left[ {{Q_2} + {Q_3} - {Q_4} - \left( {1 - \delta } \right){Q_5}} \right]{\mathscr{I}_1} - \mathscr{I}_4^{\rm{T}}\left[ {\left( {1 - } \right.} \right.\\
\left. {\left. \delta \right)\left( {{Q_2} + {Q_5}} \right) + 2{Q_4} - S - {S^{\rm{T}}}} \right]{\mathscr{I}_4} - \mathscr{I}_5^{\rm{T}}\left( {{Q_3} + {Q_4}} \right){\mathscr{I}_5} + \\
{\tau ^2}\mathscr{I}_2^{\rm{T}}\left[ {{Q_4} + {Q_5}} \right]{\mathscr{I}_2} + {M_1}{\mathscr{I}_3} + \mathscr{I}_3^{\rm{T}}{M_1} - \mathscr{I}_3^{\rm{T}}{P_2}{\mathscr{I}_3} - \\
\mathscr{I}_{13}^{\rm{T}}{P_3}{\mathscr{I}_3} - \mathscr{I}_3^{\rm{T}}{P_3}{\mathscr{I}_{13}} + \mathscr{I}_1^{\rm{T}}\left[ {{Q_4} + \left( {1 - \delta } \right){Q_5} - S} \right]{\mathscr{I}_4} + \\
\mathscr{I}_4^{\rm{T}}{\left[ {{Q_4} + \left( {1 - \delta } \right){Q_5} - S} \right]^{\rm{T}}}{\mathscr{I}_1} + \mathscr{I}_1^{\rm{T}}S{\mathscr{I}_5} + \mathscr{I}_5^{\rm{T}}S{\mathscr{I}_1} + \\
\mathscr{I}_4^{\rm{T}}\left( {{Q_4} - S} \right){\mathscr{I}_5} + \mathscr{I}_5^{\rm{T}}{\left( {{Q_4} - S} \right)^{\rm{T}}}{\mathscr{I}_4} + \mathscr{I}_1^{\rm{T}}{P_1}{\mathscr{I}_2} + \mathscr{I}_2^{\rm{T}}{P_1}{\mathscr{I}_1},
\end{array}
$
|
|
$
\begin{array}{l}
{\mathit{\Omega }_2} = {\beta _1}\left[ {\mathscr{I}_1^{\rm{T}}\left( {{I_{N - 1}} \otimes \left( {{L^{\rm{T}}}L} \right)} \right){\mathscr{I}_1} - \mathscr{I}_6^{\rm{T}}{\mathscr{I}_6}} \right] + {F_1}\left[ {\mathscr{A} + } \right.\\
\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){\mathscr{I}_{13}}} \right] - bv\mathscr{I}_3^{\rm{T}}{P_4}{\mathscr{I}_3} + \left[ {\mathscr{A} + } \right.\\
{\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){\mathscr{I}_{13}}} \right]^{\rm{T}}}F_1^{\rm{T}} + h\left[ {\mathscr{I}_2^{\rm{T}}{Q_1}{\mathscr{I}_2} + \mathscr{I}_3^{\rm{T}}{P_2}{\mathscr{I}_2} + } \right.\\
\left. {\mathscr{I}_2^{\rm{T}}{P_2}{\mathscr{I}_3} + \mathscr{I}_{13}^{\rm{T}}{P_3}{\mathscr{I}_2} + \mathscr{I}_2^{\rm{T}}{P_3}{\mathscr{I}_{13}}} \right],
\end{array}
$
|
|
$
\begin{array}{l}
{\mathit{\Omega }_3} = {\beta _2}\left[ {\mathscr{I}_1^{\rm{T}}\left( {{I_{N - 1}} \otimes \left( {{L^{\rm{T}}}L} \right)} \right){\mathscr{I}_1} - \mathscr{I}_6^{\rm{T}}{\mathscr{I}_6}} \right] + {F_2}\left[ {\mathscr{A} + } \right.\\
\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){\mathscr{I}_{13}}} \right] - bv\mathscr{I}_3^{\rm{T}}{P_5}{\mathscr{I}_3} + \left[ {\mathscr{A} + } \right.\\
{\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){\mathscr{I}_{13}}} \right]^{\rm{T}}}F_2^{\rm{T}},
\end{array}
$
|
|
$
{\mathit{\Omega }_{12}} = \frac{1}{2}\mathscr{I}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right) + \left( {h\mathscr{I}_2^{\rm{T}} - \frac{{av}}{2}\mathscr{I}_3^{\rm{T}}} \right){P_4},
$
|
|
$
{\mathit{\Omega }_{22}} = \frac{1}{2}\mathscr{I}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right) + \left( {h\mathscr{I}_2^{\rm{T}} - \frac{{av}}{2}\mathscr{I}_3^{\rm{T}}} \right){P_5},
$
|
|
$
\begin{array}{l}
{F_1} = {\left( {{F_{11}},{F_{12}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 4n\left( {N - 1} \right)}}} \right)^{\rm{T}}},{F_2} = \left( {{F_{21}},{F_{22}},} \right.\\
{\left. {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 4n\left( {N - 1} \right)}}} \right)^{\rm{T}}}.
\end{array}
$
|
则同步误差系统(9)关于S(h)为UGES.
证明 从式(16)可知,存在充分小的正标量c0>0,使得V(t)≥c0‖e(t)‖2.根据所定义的时间依赖的Lyapunov函数(14)可知:
|
$
\begin{array}{l}
V\left( t \right) \ge {e^{\rm{T}}}\left( t \right){P_1}e\left( t \right) + {\rho _2}\left( t \right)\left[ {{{\tilde e}^{\rm{T}}}\left( t \right){P_2}\tilde e\left( t \right) + } \right.\\
\left. {2\left( {e\left( t \right) - \tilde e\left( t \right)} \right){P_3}\tilde e\left( t \right)} \right] + {\rho _2}\left( t \right)\int_{t - {\rho _1}\left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_1}\dot e\left( s \right){\rm{d}}s} .
\end{array}
$
|
(18) |
又根据引理2和式(8)可得下式成立,
|
$
\begin{array}{l}
\frac{1}{h}{{\tilde e}^{\rm{T}}}\left( t \right){Q_1}\tilde e\left( t \right) \le \frac{1}{{{\rho _1}\left( t \right)}}{{\tilde e}^{\rm{T}}}\left( t \right){Q_1}\tilde e\left( t \right) \le \\
\int_{t - {\rho _1}\left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_1}\dot e\left( s \right){\rm{d}}s} .
\end{array}
$
|
(19) |
把式(19)代入式(18)中有
|
$
\begin{array}{l}
V\left( t \right) \ge \\
{\left[ \begin{array}{l}
e\left( t \right)\\
\tilde e\left( t \right)
\end{array} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}}
{{P_1}}&{{\rho _2}\left( t \right){P_3}}\\
* &{{\rho _2}\left( t \right)\left[ {\frac{1}{h}{Q_1} + {P_2} - {P_3} - P_3^{\rm{T}}} \right]}
\end{array}} \right] \cdot \\
\left[ \begin{array}{l}
e\left( t \right)\\
\tilde e\left( t \right)
\end{array} \right] = {\left[ \begin{array}{l}
e\left( t \right)\\
\tilde e\left( t \right)
\end{array} \right]^{\rm{T}}}\left( {\frac{{h - {\rho _2}\left( t \right)}}{h}\left[ {\begin{array}{*{20}{c}}
{{P_1}}&0\\
* &0
\end{array}} \right] + \frac{{{\rho _2}\left( t \right)}}{h} \cdot } \right.\\
\left. {\left[ {\begin{array}{*{20}{c}}
{{P_1}}&{h{P_3}}\\
* &{{Q_1} + h\left[ {{P_2} - {P_3} - P_3^{\rm{T}}} \right]}
\end{array}} \right]} \right)\left[ \begin{array}{l}
e\left( t \right)\\
\tilde e\left( t \right)
\end{array} \right].
\end{array}
$
|
(20) |
所以根据(16)可得:
|
$
V\left( t \right) \ge \frac{{h - {\rho _2}\left( t \right)}}{h}{e^{\rm{T}}}\left( t \right){P_1}e\left( t \right).
$
|
又因为P1>0,所以存在充分小的正标量c0>0,使得V(t)≥c0‖e(t)‖2.
又根据矩阵不等式(17)可知,存在充分小的正标量ε1,并令h=h+ε1,使得下列矩阵不等式成立:
|
$
\left[ {\begin{array}{*{20}{c}}
{{\Omega _1} + {{\Omega '}_2}}&{{{\Omega '}_{12}}}\\
* &{ - \nu \frac{h}{{\bar h}}{P_4}}
\end{array}} \right] < 0,
$
|
(21) |
|
$
\left[ {\begin{array}{*{20}{c}}
{{\Omega _1} + {{\Omega '}_3}}&{{{\Omega '}_{22}}}&{h{M_1}}\\
* &{ - \nu \frac{h}{{\bar h}}{P_5}}&0\\
*&* &{ - h{Q_1}}
\end{array}} \right] < 0,
$
|
(22) |
其中
|
$
\begin{array}{l}
{{\mathit{\Omega '}}_2} = {\mathit{\Omega }_2} + \left( {1 - \frac{h}{{\bar h}}} \right)bv\mathscr{I}_3^{\rm{T}}{P_4}{\mathscr{I}_3},{{\mathit{\Omega '}}_3} = {\mathit{\Omega }_3} + \\
\left( {1 - \frac{h}{{\bar h}}} \right)bv\mathscr{I}_3^{\rm{T}}{P_5}{\mathscr{I}_3},
\end{array}
$
|
|
$
\begin{array}{l}
{{\mathit{\Omega '}}_{12}} = {\mathit{\Omega }_{12}} + \left( {1 - \frac{h}{{\bar h}}} \right)\frac{{av}}{2}\mathscr{I}_3^{\rm{T}}{P_4},{{\mathit{\Omega '}}_{22}} = {\mathit{\Omega }_{22}} + \left( {1 - } \right.\\
\left. {\frac{h}{{\bar h}}} \right)\frac{{av}}{2}\mathscr{I}_3^{\rm{T}}{P_5},
\end{array}
$
|
令
|
$
{\mathit{\Xi }_1} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\Omega }_1}}&{\frac{1}{2}\mathscr{I}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right)}\\
* &0
\end{array}} \right],
$
|
|
$
{\mathit{\Xi }_2} = \left[ {\begin{array}{*{20}{c}}
{\frac{1}{h}{{\mathit{\Omega '}}_2}}&{\left( {\mathscr{I}_2^{\rm{T}} - \frac{{av}}{{\bar h}}\mathscr{I}_3^{\rm{T}}} \right){P_4}}\\
* &{ - \frac{v}{{\bar h}}{P_4}}
\end{array}} \right],
$
|
|
$
{\mathit{\Xi }_3} = \left[ {\begin{array}{*{20}{c}}
{{{\mathit{\bar \Omega '}}_3}}&{\left( {\mathscr{I}_2^{\rm{T}} - \frac{{av}}{{2\bar h}}\mathscr{I}_3^{\rm{T}}} \right){P_5}}\\
* &{ - \frac{v}{{\bar h}}{P_5}}
\end{array}} \right],
$
|
|
$
\begin{array}{l}
\beta \left( t \right) = \frac{{{\rho _2}\left( t \right)}}{h}{\beta _1} + \frac{{h - {\rho _2}\left( t \right)}}{h}{\beta _2},F\left( t \right) = \frac{{{\rho _2}\left( t \right)}}{h}{F_1} + \\
\frac{{h - {\rho _2}\left( t \right)}}{h}{F_2},
\end{array}
$
|
其中${{\mathit{\bar \Omega '}}_3} = \frac{1}{h}{{\mathit{\bar \Omega '}}_3} + {M_1}Q_1^{-1}M_1^{\rm{T}}$.
所以,根据Schur补引理可知,式(21)和式(22)分别等价于下列两个矩阵不等式:
|
$
{\mathit{\Xi }_1} + h{\mathit{\Xi }_2} < 0,{\mathit{\Xi }_1} + h{\mathit{\Xi }_3} < 0.
$
|
(23) |
对Vi(t, e(t))在t∈[tk, tk+1)上沿误差系统(9)的轨线求导可得
|
$
{D^ + }{V_1}\left( {t,e\left( t \right)} \right) = 2{e^{\rm{T}}}\left( t \right){P_1}\dot e\left( t \right),
$
|
|
$
\begin{array}{l}
{D^ + }{V_2}\left( {t,e\left( t \right)} \right) = - {{\tilde e}^{\rm{T}}}\left( t \right){P_2}\tilde e\left( t \right) - 2\left( {e\left( t \right) - } \right.\\
\left. {\tilde e\left( t \right)} \right){P_3}\tilde e\left( t \right) + {\rho _2}\left( t \right)\left[ {2{{\tilde e}^{\rm{T}}}\left( t \right){P_2}\dot e\left( t \right) + 2\left( {e\left( t \right) - } \right.} \right.\\
\left. {\left. {\tilde e\left( t \right)} \right){P_3}\dot e\left( t \right)} \right],
\end{array}
$
|
|
$
\begin{array}{l}
{D^ + }{V_3}\left( {t,e\left( t \right)} \right) = \mathit{\dot \Psi }\left( t \right){{\tilde e}^{\rm{T}}}\left( t \right)\left[ {{\rho _2}\left( t \right){P_4} + \left( {h - } \right.} \right.\\
\left. {\left. {{\rho _2}\left( t \right)} \right){P_5}} \right]\tilde e\left( t \right) + 2\mathit{\Psi }\left( t \right){{\tilde e}^{\rm{T}}}\left( t \right)\left[ {{\rho _2}\left( t \right){P_4} + \left( {h - } \right.} \right.\\
\left. {\left. {{\rho _2}\left( t \right)} \right){P_5}} \right]\dot e\left( t \right) + \mathit{\Psi }\left( t \right){{\tilde e}^{\rm{T}}}\left( t \right)\left[ {{P_5} - {P_4}} \right]\tilde e\left( t \right),
\end{array}
$
|
|
$
\begin{array}{l}
{D^ + }{V_4}\left( {t,e\left( t \right)} \right) = {\rho _2}\left( t \right){{\dot e}^{\rm{T}}}\left( t \right){Q_1}\dot e\left( t \right) - \\
\int_{t - {\rho _1}\left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_1}\dot e\left( s \right){\rm{d}}s} ,
\end{array}
$
|
|
$
\begin{array}{l}
{D^ + }{V_5}\left( {t,e\left( t \right)} \right) = {e^{\rm{T}}}\left( t \right){Q_2}{e^{\rm{T}}}\left( t \right) - \left( {1 - } \right.\\
\left. {\dot \tau \left( t \right)} \right){e^{\rm{T}}}\left( {t - \tau \left( t \right)} \right){Q_2}e\left( {t - \tau \left( t \right)} \right),
\end{array}
$
|
|
$
\begin{array}{l}
{D^ + }{V_6}\left( {t,e\left( t \right)} \right) = {e^{\rm{T}}}\left( t \right){Q_3}{e^{\rm{T}}}\left( t \right) - {e^{\rm{T}}}\left( {t - } \right.\\
\left. \tau \right){Q_3}e\left( {t - \tau } \right),
\end{array}
$
|
|
$
\begin{array}{l}
{D^ + }{V_7}\left( {t,e\left( t \right)} \right) = {\tau ^2}{{\dot e}^{\rm{T}}}\left( t \right){Q_4}\dot e\left( t \right) - \\
\tau \int_{t - \tau }^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_4}\dot e\left( s \right){\rm{d}}s} ,
\end{array}
$
|
|
$
\begin{array}{l}
{D^ + }{V_8}\left( {t,e\left( t \right)} \right) = \tau \tau \left( t \right){e^{\rm{T}}}\left( t \right){Q_5}{e^{\rm{T}}}\left( t \right) - \tau \left( {t - } \right.\\
\left. {\dot \tau \left( t \right)} \right)\int_{t - \tau \left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_5}\dot e\left( s \right){\rm{d}}s} \le {\tau ^2}{{\dot e}^{\rm{T}}}\left( t \right){Q_5}\dot e\left( t \right) - \tau \left( {1 - } \right.\\
\left. \delta \right)\int_{t - \tau \left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_5}\dot e\left( s \right){\rm{d}}s} .
\end{array}
$
|
(24) |
注意到
|
$
\tilde e\left( t \right) = \int_{t - {\rho _1}\left( t \right)}^t {\dot e\left( s \right){\rm{d}}s} ,
$
|
根据引理2和式(8)可知,存在矩阵M1∈ℝ6n(N-1)×n(N-1),使得下式成立:
|
$
\begin{array}{l}
0 = 2{\xi ^{\rm{T}}}\left( t \right){M_1}\left[ {\tilde e\left( t \right) - \int_{t - {\rho _1}\left( t \right)}^t {\dot e\left( s \right){\rm{d}}s} } \right] \le \\
2{\xi ^{\rm{T}}}\left( t \right){M_1}\tilde e\left( t \right) + \left( {h - {\rho _2}\left( t \right)} \right){\xi ^{\rm{T}}}\left( t \right){M_1}{Q_1}M_1^{\rm{T}}\xi \left( t \right) + \\
\int_{t - {\rho _1}\left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_1}\dot e\left( s \right){\rm{d}}s} .
\end{array}
$
|
(25) |
又由式(15)成立可知,通过引理3,有
|
$
\begin{array}{l}
- \tau \int_{t - \tau }^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_4}\dot e\left( s \right){\rm{d}}s} - \tau \left( {1 - } \right.\\
\left. \delta \right)\int_{t - \tau }^t {{{\dot e}^{\rm{T}}}\left( s \right){Q_5}\dot e\left( s \right){\rm{d}}s} = - \tau \int_{t - \tau \left( t \right)}^t {{{\dot e}^{\rm{T}}}\left( s \right)\left[ {{Q_4} + \left( {1 - } \right.} \right.} \\
\left. {\left. \delta \right){Q_5}} \right]\dot e\left( s \right){\rm{d}}s - \tau \int_{t - \tau }^{t - \tau \left( t \right)} {{{\dot e}^{\rm{T}}}\left( s \right){Q_4}\dot e\left( s \right){\rm{d}}s} \le {\eta ^{\rm{T}}}\left( t \right){\Lambda _1}\eta \left( t \right) = \\
{\xi ^{\rm{T}}}\left( t \right)\left\{ { - \mathscr{I}_1^{\rm{T}}\left[ {{Q_4} + \left( {1 - \delta } \right){Q_5}} \right]{\mathscr{I}_1} + \mathscr{I}_4^{\rm{T}}\left[ {{Q_4} + \left( {1 - } \right.} \right.} \right.\\
{\left. {\left. \delta \right){Q_5} - S} \right)^{\rm{T}}}{\mathscr{I}_1} + \mathscr{I}_1^{\rm{T}}\left[ {{Q_4} + \left( {1 - \delta } \right){Q_5} - S} \right]{\mathscr{I}_4} + \\
\mathscr{I}_5^{\rm{T}}{S^{\rm{T}}}{\mathscr{I}_1} + \mathscr{I}_1^{\rm{T}}{S^{\rm{T}}}{\mathscr{I}_5} + \mathscr{I}_5^{\rm{T}}{\left( {{Q_4} - S} \right)^{\rm{T}}}{\mathscr{I}_4} + \mathscr{I}_4^{\rm{T}}{\left( {{Q_4} - S} \right)^{\rm{T}}}{\mathscr{I}_5} + \\
\left. {\mathscr{I}_4^{\rm{T}}\left[ { - \left( {1 - \delta } \right){Q_5} - 2{Q_4} + S + {S^{\rm{T}}}} \right]{\mathscr{I}_4} - \mathscr{I}_5^{\rm{T}}{Q_4}{\mathscr{I}_5}} \right\}\xi \left( t \right),
\end{array}
$
|
(26) |
其中
|
$
{\eta ^{\rm{T}}}\left( t \right) = \left( {{e^{\rm{T}}}\left( t \right),{e^{\rm{T}}}\left( {t - \tau \left( t \right)} \right),{e^{\rm{T}}}\left( {t - \tau } \right)} \right),
$
|
|
$
\begin{array}{l}
{\mathit{\Lambda }_1} = \\
\left[ {\begin{array}{*{20}{c}}
{ - \left[ {{Q_4} + \left( {1 - \delta } \right){Q_5}} \right]}&{{Q_4} + \left( {1 - \delta } \right){Q_5} - S}&S\\
* &{ - 2{Q_4} - \left( {1 - \delta } \right){Q_5} + S + {S^{\rm{T}}}}&{{Q_4} - S}\\
*&* &{ - {Q_4}}
\end{array}} \right].
\end{array}
$
|
根据同步误差系统(9)可知,存在矩阵F(t)∈ℝ6n(N-1)×n(N-1)使得下式恒成立:
|
$
\begin{array}{l}
0 = 2{\xi ^{\rm{T}}}\left( t \right)F\left( t \right)\left[ {\left( {{I_{N - 1}} \otimes A} \right)e\left( t \right) - \dot e\left( t \right) + \bar f\left( {t,} \right.} \right.\\
\left. {x\left( t \right)} \right) + \left( {\left( {GBM} \right) \otimes \mathit{\Gamma }} \right)e\left( {t - \tau \left( t \right)} \right) + \\
\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right)e\left( {t - {\rho _1}\left( t \right)} \right)} \right],
\end{array}
$
|
根据所引入的符号,上式可以写为如下形式:
|
$
\begin{array}{l}
0 = {\xi ^{\rm{T}}}\left( t \right)\left\{ {F\left( t \right)\left[ {\mathscr{A} + \left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){\mathscr{I}_{13}}} \right] + \left[ {\mathscr{A} + } \right.} \right.\\
\left. {{{\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){\mathscr{I}_{13}}} \right]}^{\rm{T}}}{F^{\rm{T}}}\left( t \right)} \right\}\xi \left( t \right).
\end{array}
$
|
(27) |
又由假设(H1)知,存在标量β(t)>0,使得下面的不等式恒成立:
|
$
\begin{array}{l}
0 \le \beta \left( t \right)\left[ {{e^{\rm{T}}}\left( t \right)\left( {{I_{N - 1}} \otimes \left( {{L^{\rm{T}}}L} \right)e\left( t \right) - {{\bar f}^{\rm{T}}}\left( {t,} \right.} \right.} \right.\\
\left. {\left. {x\left( t \right)} \right)\bar f\left( {t,x\left( t \right)} \right)} \right].
\end{array}
$
|
(28) |
把式(25)~(28)代入式(24),并根据假设(H2)可得
|
$
\begin{array}{l}
{D^ + }V\left( t \right) \le \\
{\left[ {\begin{array}{*{20}{c}}
{\xi \left( t \right)}\\
{\mathit{\Psi }\left( t \right)\tilde e\left( t \right)}
\end{array}} \right]^{\rm{T}}}\left[ {{\mathit{\Xi }_1} + {\rho _2}\left( t \right){\mathit{\Xi }_2} + \left( {h - {\rho _2}\left( t \right)} \right){\mathit{\Xi }_3}} \right] \cdot \\
\left[ {\begin{array}{*{20}{c}}
{\xi \left( t \right)}\\
{\mathit{\Psi }\left( t \right)\tilde e\left( t \right)}
\end{array}} \right] = {\left[ {\begin{array}{*{20}{c}}
{\xi \left( t \right)}\\
{\mathit{\Psi }\left( t \right)\tilde e\left( t \right)}
\end{array}} \right]^{\rm{T}}}\left[ {\frac{{{\rho _2}\left( t \right)}}{2}\left[ {{\mathit{\Xi }_1} + h{\mathit{\Xi }_2}} \right] + } \right.\\
\left. {\frac{{h - {\rho _2}\left( t \right)}}{h}\left[ {{\mathit{\Xi }_1} + h{\mathit{\Xi }_3}} \right]} \right]\left[ {\begin{array}{*{20}{c}}
{\xi \left( t \right)}\\
{\mathit{\Psi }\left( t \right)\tilde e\left( t \right)}
\end{array}} \right].
\end{array}
$
|
(29) |
通过式(23)可得D+V(t) < 0.即,存在一个充分小的γ>0使得
|
$
{D^ + }V\left( t \right) \leqslant - \gamma {\xi ^{\rm{T}}}\left( t \right)\xi \left( t \right),t \in \left[ {{t_k},{t_{k + 1}}} \right),k \in \mathbb{N}.
$
|
(30) |
现在考虑V(t)在采样时刻tk, k∈$\mathbb{N}$的取值.注意到ρ1(tk)=ρ2(tk-)=Ψ(tk-)=0,且ẽ(tk)=0.所以有
|
$
\begin{array}{l}
V\left( {{t_k}} \right) = {V_1}\left( {{t_k}} \right) + {V_5}\left( {{t_k}} \right) + {V_6}\left( {{t_k}} \right) + {V_7}\left( {{t_k}} \right) + \\
{V_8}\left( {{t_k}} \right) = {V_1}\left( {t_k^ - } \right) + {V_5}\left( {t_k^ - } \right) + {V_6}\left( {t_k^ - } \right) + {V_7}\left( {t_k^ - } \right) + \\
{V_8}\left( {t_k^ - } \right) = V\left( {t_k^ - } \right).
\end{array}
$
|
(31) |
ρ2(t)和Ψ(t)在[t0, +∞)上有界,Lyapunov函数V(t)在[t0, +∞)上连续.所以,存在正标量c1, c2,使得下式成立:
|
$
V\left( t \right) \le {c_1}{\left\| {\xi \left( t \right)} \right\|^2} + {c_2}\int_{t - \bar \tau }^t {{{\left\| {\xi \left( s \right)} \right\|}^2}{\rm{d}}s} ,
$
|
其中τ=max {τ, h}.
又从式(16)可知,存在充分小的正标量c0>0,使得V(t)≥c0‖e(t)‖2.则有
|
$
\begin{array}{l}
{c_0}{\left\| {e\left( t \right)} \right\|^2} \le V\left( t \right) \le {c_1}{\left\| {\xi \left( t \right)} \right\|^2} + \\
{c_2}\int_{t - \bar \tau }^t {{{\left\| {\xi \left( s \right)} \right\|}^2}} {\rm{d}}s.
\end{array}
$
|
(32) |
选取c>0,使得下式成立:
|
$
0 < \gamma - c\left( {{c_1} + {c_2}\bar \tau {e^{c\bar \tau }}} \right).
$
|
(33) |
通过式(30)和式(32),可以推得下式成立:
|
$
\begin{array}{l}
{D^ + }\left( {{e^{ct}}V\left( t \right)} \right) = {e^{ct}}\left( {cV\left( t \right) + {D^ + }V\left( t \right)} \right) \le \\
{e^{ct}}\left[ {\left( {c{c_1} - \gamma } \right){{\left\| {\xi \left( t \right)} \right\|}^2} + c{c_2}\int_{t - \bar \tau }^t {{{\left\| {\xi \left( s \right)} \right\|}^2}{\rm{d}}s} } \right],
\end{array}
$
|
(34) |
对上式两边从t0到t求积分有
|
$
\begin{array}{l}
\int_{{t_0}}^t {{D^ + }\left( {{e^{cs}}V\left( s \right)} \right){\rm{d}}s} \le \left( {c{c_1} - } \right.\\
\left. \gamma \right)\int_{{t_0}}^t {{e^{cs}}{{\left\| {\xi \left( s \right)} \right\|}^2}{\rm{d}}s} + c{c_2}\int_{{t_0}}^t {\int_{s - \bar \tau }^s {{e^{cs}}{{\left\| {\xi \left( \theta \right)} \right\|}^2}{\rm{d}}\theta {\rm{d}}s} } ,
\end{array}
$
|
(35) |
注意到
|
$
\begin{array}{l}
\int_{{t_0}}^t {\int_{s - \bar \tau }^s {{e^{cs}}{{\left\| {\xi \left( \theta \right)} \right\|}^2}{\rm{d}}\theta {\rm{d}}s} } \le \\
{e^{c\bar \tau }}\int_{{t_0} - \bar \tau }^t {\int_s^{s + \bar \tau } {{e^{cs}}{{\left\| {\xi \left( \theta \right)} \right\|}^2}{\rm{d}}\theta {\rm{d}}s} } \le \\
\bar \tau {e^{c\bar \tau }}\left( {\int_{{t_0} - \bar \tau }^t {{e^{cs}}{{\left\| {\xi \left( \theta \right)} \right\|}^2}{\rm{d}}s} + \int_{{t_0}}^t {{e^{cs}}{{\left\| {\xi \left( \theta \right)} \right\|}^2}{\rm{d}}s} } \right) \le \\
{{\bar \tau }^2}{e^{c\left( {{t_0} + \bar \tau } \right)}}\left\| \phi \right\|_{\bar \tau }^2 + \bar \tau {e^{c\bar \tau }}\int_{{t_0}}^t {{e^{cs}}{{\left\| {\xi \left( \theta \right)} \right\|}^2}{\rm{d}}s} .
\end{array}
$
|
(36) |
结合式(35)和式(36),可得
|
$
\begin{array}{l}
{e^{ct}}V\left( t \right) \le {e^{c{t_0}}}V\left( {{t_0}} \right) + c{c_2}{{\bar \tau }^2}{e^{c\left( {{t_0} + \bar \tau } \right)}}\left\| \phi \right\|_{\bar \tau }^2 + \\
\left( {c{c_1} + c{c_2}\bar \tau {e^{c\bar \tau }}} \right)\int_{{t_0}}^t {{e^{cs}}{{\left\| {\xi \left( s \right)} \right\|}^2}{\rm{d}}s} .
\end{array}
$
|
又易知
|
$
\begin{array}{l}
V\left( {{t_0}} \right) \le {c_1}{\left\| {\xi \left( {{t_0}} \right)} \right\|^2} + {c_2}\int_{{t_0} - \bar \tau }^{{t_0}} {{{\left\| {\xi \left( s \right)} \right\|}^2}{\rm{d}}s} \le \\
\left( {{c_1} + {c_2}\bar \tau } \right)\left\| \phi \right\|_{\bar \tau }^2,
\end{array}
$
|
(37) |
通过式(33)和式(37),有
|
$
{e^{ct}}V\left( t \right) \le \left( {{c_1} + {c_2}\bar \tau + c{c_2}\bar \tau {e^{c\bar \tau }}} \right)\left\| \phi \right\|_{\bar \tau }^2{e^{c{t_0}}},
$
|
则有
|
$
\left\| {e\left( t \right)} \right\| \le K{\left\| \phi \right\|_{\bar \tau }}{e^{ - \frac{1}{2}c\left( {t - {t_0}} \right)}},\forall t > {t_0},
$
|
其中$K = \sqrt {\frac{{{c_1} + {c_2}\bar \tau + c{c_2}\bar \tau {e^{c\bar \tau }}}}{{{c_0}}}} $.
因此,同步误差系统(9)的零解关于S(h)为UGES.
在文献[12]中,考虑了没有耦合时滞的复杂动态网络,其形式如下:
|
$
\begin{gathered}
{{\dot x}_i}\left( t \right) = A{x_i}\left( t \right) + f\left( {t,{x_i}\left( t \right)} \right) + \sum\limits_{j \in {N_i}} {{\nu _{ij}}\mathit{\Gamma }\left( {{x_j}\left( {{t_k}} \right) - } \right.} \hfill \\
\left. {{x_i}\left( {{t_k}} \right)} \right),t \in \left[ {{t_k},{t_{k + 1}}} \right),k \in \mathbb{N}. \hfill \\
\end{gathered}
$
|
(38) |
根据本文所构造的时间依赖的Lyapunov函数,定理1中的条件可以进行简化.具体方法如下:重新构造结构更为简单的时间依赖的Lyapunov函数:
|
$
V\left( t \right) \buildrel \Delta \over = \bar V\left( {t,e\left( t \right)} \right) = \sum\limits_{i = 1}^4 {{V_i}\left( {t,e\left( t \right)} \right)} ,
$
|
(39) |
其中Vi(t, e(t))如式(14)中所定义.则定理1可以简化为如下推论的形式:
推论1 考虑CDNs(38)满足(H1).给定一个N×N维增益矩阵Δ,一类采样时间序列S(h).若存在标量βj>0, j=1, 2, 和标量a, b满足b>0, $a >-2\sqrt b $,n(N-1)×n(N-1)维矩阵P1>0, P4>0, P5>0, Qi>0, P2T=P2, P3, F11, F12, F21, F22, i=1, …, 5, 和4n(N-1)×n(N-1)维矩阵M1,使得下列矩阵不等式成立:
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\bar \Omega }}_1} + {{\mathit{\bar \Omega }}_2}}&{{{\mathit{\bar \Omega }}_{12}}}\\
* &{ - \nu {P_4}}
\end{array}} \right] < 0,\\
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\bar \Omega }}_1} + {{\mathit{\bar \Omega }}_3}}&{{{\mathit{\bar \Omega }}_{22}}}&{h{{\bar M}_1}}\\
* &{ - \nu {P_5}}&0\\
*&* &{ - h{Q_1}}
\end{array}} \right] < 0,
\end{array}
$
|
(40) |
其中
|
$
{{\bar {\mathscr{I}}}_1} = \left[ {{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 3n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\bar {\mathscr{I}}}_2} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\bar {\mathscr{I}}}_3} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\bar {\mathscr{I}}}_4} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 3n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\bar {\mathscr{I}}}_{13}} = \left[ {{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}, - {\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
\bar {\mathscr{A}} = \left[ {\left( {{\mathit{\boldsymbol{I}}_{\left( {N - 1} \right)}} \otimes A} \right), - {\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
\begin{array}{l}
{{\mathit{\bar \Omega }}_1} = \bar {\mathscr{I}}_1^{\rm{T}}{P_1}{{\bar {\mathscr{I}}}_2} + \bar {\mathscr{I}}_2^{\rm{T}}{P_1}{{\bar {\mathscr{I}}}_1} + {{\bar M}_1}{{\bar {\mathscr{I}}}_3} + \bar {\mathscr{I}}_3^{\rm{T}}{{\bar M}_1} - \bar {\mathscr{I}}_3^{\rm{T}}{P_2}{{\bar {\mathscr{I}}}_3} - \\
\bar {\mathscr{I}}_{13}^{\rm{T}}{P_3}{\mathscr{I}_3} - \bar {\mathscr{I}}_3^{\rm{T}}{P_3}{{\bar {\mathscr{I}}}_{13}},
\end{array}
$
|
|
$
\begin{array}{l}
{{\mathit{\bar \Omega }}_2} = {\beta _1}\left[ {\bar {\mathscr{I}}_1^{\rm{T}}\left( {{I_{N - 1}} \otimes \left( {{L^{\rm{T}}}L} \right)} \right){{\bar {\mathscr{I}}}_1} - \bar {\mathscr{I}}_4^{\rm{T}}{{\bar {\mathscr{I}}}_4}} \right] + {{\bar F}_1}\left[ {\bar {\mathscr{A}} + } \right.\\
\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){{\bar {\mathscr{I}}}_{13}}} \right] - bv\bar {\mathscr{I}}_3^{\rm{T}}{P_4}{{\bar {\mathscr{I}}}_3} + \left[ {\bar {\mathscr{A}} + } \right.\\
{\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){{\bar {\mathscr{I}}}_{13}}} \right]^{\rm{T}}}\bar F_1^{\rm{T}} + h\left[ {\bar {\mathscr{I}}_2^{\rm{T}}{Q_1}{{\bar {\mathscr{I}}}_2} + \bar {\mathscr{I}}_3^{\rm{T}}{P_2}{{\bar {\mathscr{I}}}_2} + } \right.\\
\left. {\bar {\mathscr{I}}_2^{\rm{T}}{P_2}{{\bar {\mathscr{I}}}_3} + \bar {\mathscr{I}}_{13}^{\rm{T}}{P_3}{{\bar {\mathscr{I}}}_2} + \bar {\mathscr{I}}_2^{\rm{T}}{P_3}{{\bar {\mathscr{I}}}_{13}}} \right],
\end{array}
$
|
|
$
\begin{array}{l}
{{\mathit{\bar \Omega }}_3} = {\beta _2}\left[ {\bar {\mathscr{I}}_1^{\rm{T}}\left( {{I_{N - 1}} \otimes \left( {{L^{\rm{T}}}L} \right)} \right){{\bar {\mathscr{I}}}_1} - \bar {\mathscr{I}}_4^{\rm{T}}{{\bar {\mathscr{I}}}_4}} \right] + {{\bar F}_2}\left[ {\bar {\mathscr{A}} + } \right.\\
\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){{\bar {\mathscr{I}}}_{13}}} \right] - bv\bar {\mathscr{I}}_3^{\rm{T}}{P_5}{{\bar {\mathscr{I}}}_3} + \left[ {\bar {\mathscr{A}} + } \right.\\
{\left. {\left( {\left( {G\Delta M} \right) \otimes \mathit{\Gamma }} \right){{\bar {\mathscr{I}}}_{13}}} \right]^{\rm{T}}}\bar F_2^{\rm{T}},
\end{array}
$
|
|
$
{{\mathit{\bar \Omega }}_{12}} = \frac{1}{2}\bar {\mathscr{I}}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right) + \left( {h\bar {\mathscr{I}}_2^{\rm{T}} - \frac{{av}}{2}\bar {\mathscr{I}}_3^{\rm{T}}} \right){P_4},
$
|
|
$
{{\mathit{\bar \Omega }}_{22}} = \frac{1}{2}\bar {\mathscr{I}}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right) + \left( {h\bar {\mathscr{I}}_2^{\rm{T}} - \frac{{av}}{2}\bar {\mathscr{I}}_3^{\rm{T}}} \right){P_5},
$
|
|
$
\begin{array}{l}
{{\bar F}_1} = {\left( {{F_{11}},{F_{12}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}}} \right)^{\rm{T}}},{{\bar F}_2} = \left( {{F_{21}},{F_{22}},} \right.\\
{\left. {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}}} \right)^{\rm{T}}}.
\end{array}
$
|
则CDNs(38)关于S(h)是一致全局指数同步的.
当f=0时,系统(39)变为如下形式:
|
$
\begin{array}{l}
{{\dot x}_i}\left( t \right) = A{x_i}\left( t \right) + \sum\limits_{j \in {N_i}} {{\nu _{ij}}\mathit{\Gamma }\left( {{x_j}\left( {{t_k}} \right) - {x_i}\left( {{t_k}} \right)} \right)} ,t \in \\
\left[ {{t_k},{t_{k + 1}}} \right),k \in N.
\end{array}
$
|
(41) |
根据所构造的时间依赖的Lyapunov(39)函数,可以得到如下推论:
推论2 考虑CDNs(41),给定一个N×N维增益矩阵Δ,一类采样时间序列S(h).若存在标量βj>0, j=1, 2, 和标量a, b满足b>0, $a >-2\sqrt b $,n(N-1)×n(N-1)维矩阵P1>0, P4>0, P5>0, Qi>0, P2T=P2, P3, F11, F12, F21, F22, i=1, …, 5, 和3n(N-1)×n(N-1)维矩阵${{\tilde M}_1}$,使得下列矩阵不等式成立:
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\tilde \Omega }}_1} + {{\mathit{\tilde \Omega }}_2}}&{{{\mathit{\tilde \Omega }}_{12}}}\\
* &{ - \nu {P_4}}
\end{array}} \right] < 0,\\
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\tilde \Omega }}_1} + {{\mathit{\tilde \Omega }}_3}}&{{{\mathit{\tilde \Omega }}_{22}}}&{h{{\tilde M}_1}}\\
* &{ - \nu {P_5}}&0\\
*&* &{ - h{Q_1}}
\end{array}} \right] < 0,
\end{array}
$
|
(42) |
其中
|
$
{{\tilde {\mathscr{I}}}_1} = \left[ {{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\tilde {\mathscr{I}}}_2} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\tilde {\mathscr{I}}}_3} = \left[ {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right) \times 2n\left( {N - 1} \right)}},{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
{{\tilde {\mathscr{I}}}_{13}} = \left[ {{\mathit{\boldsymbol{I}}_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}, - {I_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
\tilde {\mathscr{A}} = \left[ {\left( {{I_{\left( {N - 1} \right)}} \otimes A} \right), - {I_{n\left( {N - 1} \right)}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}} \right],
$
|
|
$
\begin{array}{l}
{{\mathit{\tilde \Omega }}_1} = {{\tilde M}_1}{{\tilde {\mathscr{I}}}_3} + \tilde {\mathscr{I}}_3^{\rm{T}}{{\tilde M}_1} - \tilde {\mathscr{I}}_3^{\rm{T}}{P_2}{{\tilde {\mathscr{I}}}_3} - \tilde {\mathscr{I}}_{13}^{\rm{T}}{P_3}{{\tilde {\mathscr{I}}}_3} - \\
\tilde {\mathscr{I}}_3^{\rm{T}}{P_3}{{\tilde {\mathscr{I}}}_{13}} + \tilde {\mathscr{I}}_1^{\rm{T}}{P_1}{{\tilde {\mathscr{I}}}_2} + \tilde {\mathscr{I}}_2^{\rm{T}}{P_1}{{\tilde {\mathscr{I}}}_1},
\end{array}
$
|
|
$
\begin{array}{l}
{{\mathit{\tilde \Omega }}_2} = {{\tilde F}_1}\left[ {\tilde {\mathscr{A}} + \left( {\left( {GVM} \right) \otimes \mathit{\Gamma }} \right){{\tilde {\mathscr{I}}}_{13}}} \right] + \left[ {\tilde {\mathscr{A}} + } \right.\\
{\left. {\left( {\left( {GVM} \right) \otimes \mathit{\Gamma }} \right){{\tilde {\mathscr{I}}}_{13}}} \right]^{\rm{T}}}\tilde F_1^{\rm{T}} - bv\bar {\mathscr{I}}_3^{\rm{T}}{P_4}{{\bar {\mathscr{I}}}_3} + h\left[ {\tilde {\mathscr{I}}_2^{\rm{T}}{Q_1}{{\tilde {\mathscr{I}}}_2}} \right. + \\
\left. {\bar {\mathscr{I}}_3^{\rm{T}}{P_2}{{\bar {\mathscr{I}}}_2} + \bar {\mathscr{I}}_2^{\rm{T}}{P_2}{{\bar {\mathscr{I}}}_3} + \bar {\mathscr{I}}_{13}^{\rm{T}}{P_3}{{\bar {\mathscr{I}}}_2} + \bar {\mathscr{I}}_2^{\rm{T}}{P_3}{{\bar {\mathscr{I}}}_{13}}} \right],
\end{array}
$
|
|
$
\begin{array}{l}
{{\mathit{\tilde \Omega }}_3} = {{\tilde F}_2}\left[ {\tilde {\mathscr{A}} + \left( {\left( {GVM} \right) \otimes \mathit{\Gamma }} \right){{\tilde {\mathscr{I}}}_{13}}} \right] + \left[ {\tilde {\mathscr{A}} + } \right.\\
{\left. {\left( {\left( {GVM} \right) \otimes \mathit{\Gamma }} \right){{\tilde {\mathscr{I}}}_{13}}} \right]^{\rm{T}}}\tilde F_2^{\rm{T}} - bv\bar {\mathscr{I}}_3^{\rm{T}}{P_5}{{\bar {\mathscr{I}}}_3},
\end{array}
$
|
|
$
{{\mathit{\tilde \Omega }}_{12}} = \frac{1}{2}{\mathscr{I}}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right) + \left( {h\tilde {\mathscr{I}}_2^{\rm{T}} - \frac{{av}}{2}\tilde {\mathscr{I}}_3^{\rm{T}}} \right){P_4},
$
|
|
$
{{\mathit{\bar \Omega }}_{22}} = \frac{1}{2}\tilde {\mathscr{I}}_3^{\rm{T}}\left( {{P_5} - {P_4}} \right) + \left( {h\tilde {\mathscr{I}}_2^{\rm{T}} - \frac{{av}}{2}\tilde {\mathscr{I}}_3^{\rm{T}}} \right){P_5},
$
|
|
$
\begin{array}{l}
\tilde F = {\left( {{F_{11}},{F_{12}},{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}} \right)^{\rm{T}}},{{\tilde F}_2} = \left( {{F_{21}},{F_{22}},} \right.\\
{\left. {{\mathit{\boldsymbol{0}}_{n\left( {N - 1} \right)}}} \right)^{\rm{T}}},
\end{array}
$
|
则CDNs(41)关于S(h)是一致全局指数同步的.
3 分布采样控制器的优化设计 在分布采样同步控制器(3)中,νij表示第j个节点与第i个节点的耦合控制力,i, j∈N,νij越小,表示控制器消耗的能量越小.因此,有必要设计一个具有最小耦合力的分布采样同步控制器,使得$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {{\nu _{ij}}} $取得最小值.但是定理1中只给出了分布采样增益矩阵Δ所要满足的条件,并没有指出如何选取合适的νij使得$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {{\nu _{ij}}} $取得最小值.下面,通过定理1给出一个优化算法来设计次优的分布采样控制器,使得其耦合力尽可能的小.
根据定理1,设计具有最小耦合力的分布采样同步控制器问题可以转化为如下的优化问题:
|
$
\begin{array}{l}
{\rm{Minimize}}\;\sum\limits_{\left( {i,j} \right) \in \varepsilon } {{\nu _{ij}}} \\
{\rm{subject}}\;{\rm{to}}\;\left( {15} \right) - \left( {17} \right).
\end{array}
$
|
(43) |
注意到(GΔMⓧΓ)$\mathscr{I}$13不是线性的,所以定理1中的条件(17)不是LMI.因此,(43)的的最优解不能通过凸优化算法来求解.在此,提出一个迭代算法来寻找优化问题(43)的次优值.
算法1:
Step 1:设k=1.取F1, F2的初值F10=F20=[2In(N-1), In(N-1), 0 n(N-1)×4n(N-1)]T.对于给定的标量a, b,满足引理1,对定理1中的变量(Pl, Qp, βq, νij)求解以下凸优化问题:
|
$
\begin{array}{l}
{\rm{Minimize}}\;\sum\limits_{\left( {i,j} \right) \in \varepsilon } {{\nu _{ij}}} \\
{\rm{subject}}\;{\rm{to}}\;\left( {15} \right) - \left( {17} \right),
\end{array}
$
|
(44) |
令(Plf, Qpf, βqf, vijf)是优化问题(44)满足$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {\nu _{ij}^f} $取到次优值的一个可行性解.设ν0=$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {\nu _{ij}^f} $, 且ν0=ν1.
Step 2:取vij=vijf,则分布采样增益矩阵Δ已知.对变量(Pl, Qp, βq,F1, F2)求解LMIs(15)-(17).令(Ptf, Qpf, βqf, F1f, F2f)是其一个可行性解.
Step 3:取F1=F1f, F2=F2f, 对变量(Pl, Qp, βq, νij)求解凸优化问题(44).令(Plf, Qpf, βqf, vijf)是优化问题(44)满足$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {\nu _{ij}^f} $取到次优值的一个可行性解.设ν0=$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {\nu _{ij}^f} $.如果ν0>ν1或是算法满足迭代次数的要求了,则算法终止.否则,设k=k+1,继续返回到Step 2.
Step 4:对满足引理1的标量a, b,运用二维搜索,可以求解出一个次优的ν0.
注4 对于推论1,可以得到类似的求解次优的分布采样同步控制器的算法,只需将算法1中的约束条件(15)-(17)应相应地改为(16)和(40).类似的,将算法1中的约束条件(15)-(17)相应改为(16)和(42),则可得到针对系统(41)的求解次优分布采样同步控制器的算法.
4 数值实例 例1 考虑一个没有耦合时滞的Chua’s电路,则CDNs(2)可以简化为如下形式:
|
$
A = \left[ {\begin{array}{*{20}{c}}
{ - \vartheta {m_1}}&\vartheta &0\\
1&{ - 1}&1\\
0&{ - \varphi }&0
\end{array}} \right],
$
|
|
$
\begin{array}{l}
f\left( {t,{x_i}} \right) = \left[ {\begin{array}{*{20}{c}}
{\frac{{\vartheta \left( {{m_1} - {m_0}} \right)}}{2}\left( {\left| {{x_{i1}} + 1} \right| - \left| {{x_{i1}} - 1} \right|} \right)}\\
0\\
0
\end{array}} \right],\\
n = 3,i = 1, \cdots ,4.
\end{array}
$
|
其中ϑ=9, φ=14.286, ${m_0} =-\frac{1}{7}, {m_1} = \frac{2}{7}$.容易看出f(t, xi)是满足假设(H1)的,且L=[ϑ(m1-m0) 0 0].
设分布采样控制器(3)的增益矩阵Δ的结构如下:
|
$
\Delta = \left[ {\begin{array}{*{20}{c}}
{ - {\nu _{14}}}&0&0&{{\nu _{14}}}\\
0&{ - {\nu _{24}}}&0&{{\nu _{24}}}\\
0&{{\nu _{32}}}&{ - {\nu _{32}}}&0\\
0&{{\nu _{42}}}&0&{ - {\nu _{42}}}
\end{array}} \right].
$
|
(45) |
取a=0.68, b=1, Γ=I3, F1和F2的初值F10=F20=[2 I9 I9 09 I9]T, 根据推论1可求得采样区间上界的最大值h=0.0266.选取h=0.026,其他的值如上所给出.根据算法1可以求得分布采样控制器(3)的最小耦合力ν0=$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {{\nu _{ij}}} $为ν0=17.3897, 其中νij的值分别为
|
$
\begin{array}{l}
{\nu _{14}} = 4.7657,{\nu _{24}} = 2.1715,{\nu _{32}} = \\
4.1558,{\nu _{42}} = 6.2975.
\end{array}
$
|
(46) |
取初值
|
$
\begin{array}{l}
x\left( \theta \right) = \left( {1,0.5,0.4, - 1, - 0.6,0.5,2,0.5,} \right.\\
{\left. { - 0.8, - 1, - 0.2,0.3} \right)^{\rm{T}}},\theta \in \left[ { - 1,0} \right].
\end{array}
$
|
(47) |
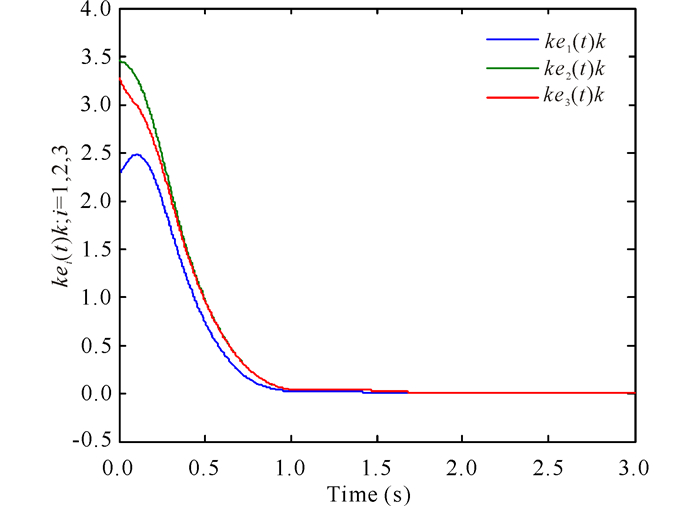
数值仿真清楚地表明,Chua’s电路的状态在没有采样控制下不能实现同步(图 1).取νij的值如式(46),在初始条件(47)下,Chua’s电路的状态在分布采样控制下实现了全局一致同步(图 2~3).
为了与文献[11]和文献[12]的结果进行比较,设系统矩阵A,内耦合矩阵G和分布采样耦合配置矩阵Δ分别为
|
$
A = \left[ {\begin{array}{*{20}{c}}
{ - 2.5}&9&0\\
1&{ - 1}&1\\
0&{ - 14}&0
\end{array}} \right],\mathit{\Gamma } = \left[ {\begin{array}{*{20}{c}}
1&0&{ - 1}\\
0&1&{ - 3}\\
{ - 1}&0&1
\end{array}} \right],
$
|
|
$
\Delta = 5 \cdot \left[ {\begin{array}{*{20}{c}}
{ - 3}&1&1&1\\
1&{ - 1}&0&0\\
1&0&{ - 2}&1\\
1&0&1&{ - 2}
\end{array}} \right].
$
|
取a=0.68, b=1, 通过推论2可求得采样区间上界的最大值h=0.0427.然而在文献[11]中所允许采样区间的最大上界值h=0.0249,文献[12]中采样区间的最大上界值h=0.0341.显然,本文所得到的结果比文献[11]和文献[12]中所得到的结果具有更少的保守性.相比于文献[11]的结果,本文所得到的采样区间上界的值提高了71.49%, 对比于文献[12],本文所得到的采样区间上界的值提高了25.22%.
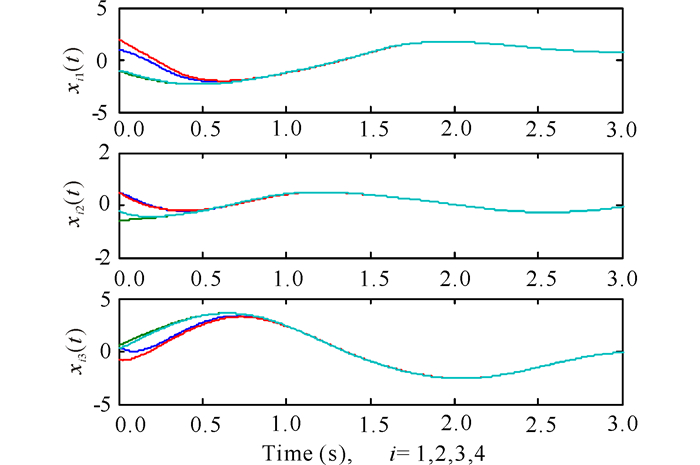
例2 考虑一个具有4个节点的Chua’s电路,系统参数表示如下:
|
$
\begin{array}{*{20}{c}}
{A = \left[ {\begin{array}{*{20}{c}}
{ - 3.2}&{10}&0\\
1&{ - 1}&1\\
0&{ - 14.87}&0
\end{array}} \right] = f\left( {t,{x_i}} \right) = }\\
{\left[ {\begin{array}{*{20}{c}}
{2.95\left( {\left| {{x_{i1}} + 1} \right| - \left| {{x_{i1}} - 1} \right|} \right)}\\
0\\
0
\end{array}} \right],n = 3,i = 1, \cdots ,4.}
\end{array}
$
|
(48) |
则根据所给出的f(t, xi)易知L=[5.9 0 0].
假设内耦合矩阵Γ=I3, τ(t)=0.04+ 0.01sin (20t),则有τ=0.05, δ=0.2.另外,设耦合配置矩阵为
|
$
B = 0.2 \cdot \left[ {\begin{array}{*{20}{c}}
{ - 1}&0&0&1\\
0&{ - 1}&0&1\\
0&1&{ - 1}&0\\
0&1&0&{ - 1}
\end{array}} \right].
$
|
根据耦合配置矩阵B的结构,分布采样控制器(3)的增益矩阵Δ的结构如式(45).
若在系统中各节点之间没有耦合,即B=0,取分布采样控制器的增益矩阵Δ为
|
$
\Delta = 10 \cdot \left[ {\begin{array}{*{20}{c}}
{ - 6}&1&2&3\\
4&{ - 15}&5&6\\
5&0&{ - 5}&0\\
6&0&0&{ - 6}
\end{array}} \right].
$
|
则取a=0.68, b=1,可求得系统的最大采样区间h=0.0129.文献[14]中的最大采样区间h=0.0120.显然,本文采用的方法放宽了采样区间的最大值,降低了保守性.
下面通过算法1来设计一个分布采样控制器且其增益矩阵形式如式(45).取初值F10=F20=[2 I9 I9 09 09 09 09]T, a=1.78, b=0.6, 可求得最大的采样区间为h=0.0187.取h=0.018,通过算法1可求得ν0=$\sum\limits_{\left( {i, j} \right) \in \varepsilon } {{\nu _{ij}}} $的最小值为25.5270.其中νij分别为
|
$
\begin{array}{l}
{\nu _{14}} = 7.2624,{\nu _{24}} = 2.8844,{\nu _{32}} = 6.1801,{\nu _{42}} = \\
9.2002.
\end{array}
$
|
(49) |
在数值仿真中,取初始条件为
|
$
\begin{array}{l}
x\left( \theta \right) = \left( {3,2,2, - 1,1,4, - 3,1,4, - 2, - 1,} \right.\\
{\left. 2 \right)^{\rm{T}}},\theta \in \left[ { - 1,0} \right].
\end{array}
$
|
(50) |
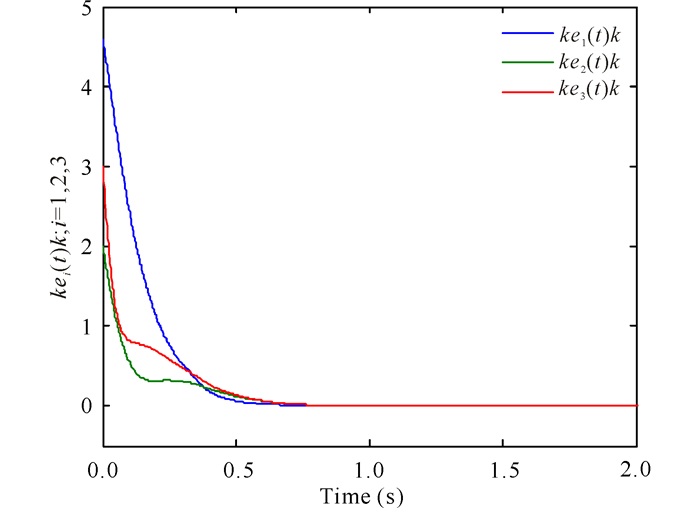
通过仿真图可知,在没有采样控制下CDNs(48)自身不能实现自同步(图 4).在相同初始条件(50)下,取νij的值如(49),CDNs(48)在分布采样控制下可以实现状态全局同步(图 5~6).
5 结论 基于分布采样控制策略,本文研究了一类具有耦合时变时滞的CDNs的状态同步问题.通过引入时间依赖的Lyapunov函数方法结合凸组合技术,运用Jensen不等式处理积分项,建立了一个具有较少保守性的分布采样同步判据,并给出了一个优化算法设计一个具有最小耦合力的分布采样控制器.所得到的判据依赖于采样区间的上界,相比于已往的研究结果,该判据放宽了采样区间的上界.
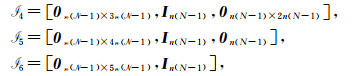



 2017, Vol. 24
2017, Vol. 24 


