2. 郑州商品交易所, 河南郑州 450008
2. Zhengzhou Commodity Exchange, Zhengzhou, Henan, 450008, China
【研究意义】集成学习是把若干个学习器集成起来对新的实例进行分类,通过对多个学习器的分类结果进行组合并决定最终的分类结果,以取得比单个学习器更好的性能。集成学习方法可以有效地提高学习系统的泛化能力,因此它已经成为机器学习领域的研究热点,被国际机器学习界的权威Dietterich称为机器学习四大研究方向之首[1]。要使得Bootstrap AGGregatING(Bagging)等集成学习算法有效,基分类器的学习算法必须是不稳定的,也就是说要对训练数据敏感。决策树就是一种不稳定的学习算法,训练集的轻微扰动会导致其学习结果发生显著的变化。因此,很多集成学习算法都将决策树作为基学习器进行集成。【前人研究进展】目前的决策树集成学习算法在训练大量的决策树之后,通常是对所有的决策树都进行集成。但是集成全部的决策树会导致高昂的存储和计算开销,使得算法在很多实际问题中难以应用。而且,当集成的决策树数目增加之后,很难得到决策树之间的差异性。因此随着集成中决策树的大量增加,决策树集成学习算法的分类性能增长很缓慢,有时反而还会降低。粗糙集是由Pawlak于20世纪80年代提出的一种数学工具,它可以用于处理不确定或不精确的知识[2]。近年来,粗糙集理论逐渐成为信息科学领域中的一个研究热点,在特征选择[3]、半监督学习[4]和数据分类[5-7]等很多方面都取得成功的应用。【本研究切入点】针对集成全部分类器时既增加内存和计算时间,有时又不能有效提高分类性能的问题,本文基于粗糙集理论提出一种新的决策树集成学习算法DTELARS。【拟解决的关键问题】基于粗糙集理论在训练的全部决策树中进行选择,只使用一部分决策树进行集成,提高决策树集成的泛化能力和效率。
1 集成学习算法 1.1 BaggingBagging(Bootstrap AGGregatING)是由Breiman提出的一种著名的集成学习算法[8]。它的基本思想是对训练集有放回地抽取训练样例,为每一个基分类器构造出一个跟训练集同样大小但各不相同的训练集,从而训练出不同的基分类器。在分类时使用投票法将这些基学习器的分类结果结合起来,并得到最终的分类结果。对于Bagging而言,基分类器的学习算法对训练数据越敏感,其效果越好。
1.2 BoostingBoosting是另一类非常有效的集成学习算法[9]。它的基本思想是对那些容易分错的训练实例加强学习。其步骤如下:首先,给每一个训练样例赋予相同的权重,然后训练第一个基学习器并用它来对训练集进行测试,对于那些分类错误的测试样例则提高其权重;其次,用调整后的带权训练集训练第二个基学习器;然后,重复这个过程直到最后得到一个足够好的学习器。
2 粗糙集粗糙集理论是有效地分析和处理不精确、不一致等各种不完备信息的数学工具。本节简要地介绍粗糙集理论的有关概念。
定义1 信息系统。四元组T=<U, A, V, f>为一个信息系统或知识表达系统,其中U为所讨论对象的集合即论域;A为属性的集合;
定义2 不可分辨关系。设有一个信息系统T=<U, A, V, f>, B
| $ \begin{array}{l} \;\;\;\;{\rm{IND}}\left( B \right) = \left\{ {\left( {x, y} \right) \in U \times U:\forall a \in {B_f}\left( {x, a} \right) = } \right.\\ \left. {f\left( {y, a} \right)} \right\}, \end{array} $ | (1) |
如果(x, y)∈IND(B),则x和y称为B不可分辨,不可分辨关系是二元关系,满足自反性、对称性和传递性。显然,不可分辨关系是T的一个等价关系。IND(B)的所有等价类族,即由B决定的划分,用U/IND(B)表示或简记为U/B,包含x的等价类用[x]B表示。
定义3 近似集合。设有一个信息系统T=<U, A, V, f>,X为U的非空子集,B
| $ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{B}X=\left\{ x\in U:{{\left[ x \right]}_{B}}\subseteq X \right\}, $ | (2) |
| $ \bar{B}X=\left\{ x\in U:{{\left[ x \right]}_{B}}\cap X\ne \varnothing \right\}, $ | (3) |
定义4 正域。POSB(X)=
| $ \text{PO}{{\text{S}}_{C}}\left( D \right)=\bigcup\limits_{X\in U/D}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{C}}}X。$ | (4) |
定义5 约简。令R为一族等价关系,A∈R,如果IND(R)=IND(R-{A}),则称A为R中不必要的;否则称A为R中必要的。如果每一个A∈R都为R中必要的,则称R为独立的;否则称R为依赖的。设P∈Q, 如果P是独立的,且IND(Q)=IND(P),则称P为Q的一个约简,记为RED(Q)。
本文采用QuickReduct算法[10]计算约简,该算法使用属性依赖度rp(D)作为属性选择准则。属性依赖度rP(D)的定义如下:
| $ {{r}_{P}}=\frac{\left\| \text{PO}{{\text{S}}_{P}}\left( D \right) \right\|}{\left\| U \right\|}。$ | (5) |
基于属性依赖度的QuickReduct约简算法如算法1所示。
算法1:QUICKREDUCT Reduction Algorithm
Input:C, the set of all conditional attributes;
D, the set of decision attributes.
Output:the reduct R of C (R
Step 1:R ← {}
Step 2:do
Step 3: T ← R
Step 4: ∀x∈(C-R)
Step 5: if γR∪{x}(D)>γT(D)
Step 6: T←R∪{x}
Step 7: R ← T
Step 8:until γR(D)=γC(D)
Step 9:return R
3 基于粗糙集理论的决策树集成学习算法本文提出的集成学习算法(DTELARS)主要包括4个步骤。
(1) 将原始训练集S随机地分为两个集合,即S1和S2。
(2) 采用可重复取样技术从集合S1中重采样出一系列新的训练集,随后从每个新的训练集中训练出一个决策树,从而得到一组决策树。
(3) 使用全部的决策树对集合S2中的样本进行分类,通过对集合S2中样本的预测标签和样本的真实标签构造出决策表。例如,假设集合S2中有M个样本,由第二步中训练得到N个决策树。每个决策树对集合S2中的每个样本都进行预测,则对集合中M个样本的预测可以表示为一个M×N矩阵W=[pij],pij表示第j个决策树对第i个样本给出的预测标签。将样本的真实标签作为决策属性,这个矩阵就构成一个决策表。在这个决策表中,每个决策树都被看作为一个条件属性,而决策树对样本的预测标签则作为条件属性的值。使用上节中介绍的QuickReduct约简算法对决策表进行约简,从而选择出全部决策树中的一个子集用于集成。
(4) 当对一个原始训练集S之外的新样本进行分类时,只使用选择的决策树对该样本进行预测,然后采用多数投票方法给出样本的最终分类结果。
详细的DTELARS如算法2所示。
Algorithm 2:Decision Tree Ensemble Learning Algorithm
Inputs:training set S, decision tree, trials T
Outputs:final classifier
Step 1:Partition the S into two sets S=S1∪S2
Step 2:Create a pool including of T decision trees
2.1.For t = 1 to T {
2.2.St = bootstrap sample from S1
2.3.Train the decision tree dtt on St
2.4.}
Step 3:Select the decision trees from the pool by using QuickReduct algorithm
3.1.Apply T decision trees in the pool to classify the examples in the S2
3.2.Construct a decision table based on the predicted class labels and real class labels of examples in the S2
3.3.Apply the QuickReduct algorithm to obtain a reduct of the decision table
Step 4:Construct the final classifier for classification
4.1.Create a combining pool including of the decision trees in the reduction
4.2.When classifying new example, only use the decision trees in the combing pool to predict example and then use major voting method to aggregate the corresponding predictions of decision trees to yield the final decision.
4 算法评价 4.1 数据集为对本文提出的集成学习算法的性能进行评价,在UCI机器学习数据库[11]中的7个数据集上进行实验。这7个数据集的具体信息如表 1所示。因为两类分类问题相对于多类分类问题更具有一般性,一个多类分类问题可以转化为一组两类分类问题来解决。因此本文中只考虑两类分类问题,即对于一个样本,或者将它分为正例,或者将它分为负例。
| 表 1 实验所用数据集 Table 1 The datasets in the experiment |
采用精度来衡量分类算法的性能。分类器对样本的分类结果有4种情况[12]:TP,被正确地分类为属于此类别的样本数量;TN,被正确地分类为不属于此类别的样本数量;FP,被错误地分类为属于此类别的样本数量;FN,被错误地分类为不属于此类别的样本数量。
根据以上4种情况,分类性能可以按照精度来评价,精度的定义如下:
| $ \text{Accuracy=}\frac{\text{TP+TN}}{\text{TP+TN+FP+FN}}。$ | (6) |
实验中以两个流行的集成学习算法Bagging和Boosting作为基准,对本文提出的算法DTELARS性能进行评价。实验中,对于Boosting采用的是AdaBoost.M1算法[9];对于决策树采用的是C4.5算法[13]。同时为比较性能,实验中也包括了使用单个决策树进行分类得到的结果。分类性能的评价方法采用的是十折交叉验证法。在实验中分别设置Bagging和Boosting的集成规模(集成中决策树的数目)从10个到50个。以此来比较集成规模的变化对DTELARS、Bagging和Boosting性能产生的影响。
当集成的规模设置为10个,即DTELARS是从10个训练决策树中进行选择和集成,Bagging和Boosting是分别训练和使用10个决策树进行集成,不同算法得到的分类精度如表 2所示。表 2最后一列为DTELARS集成中决策树的平均数目,表中的avg表示在全部数据集上分类精度的平均值。如表 2所示,DTELARS得到的平均分类精度为87.43%,比仅使用一个决策树进行分类的平均精度高出3.48%,比Bagging高出1.92%,比Boosting高出1.40%,DTELARS在所有数据集上的平均分类精度均超过其它的算法。由DTELARS创建的集成中所使用的决策树数目仅是Bagging和Boosting使用数目的54%(5.4/10.0)。
| 表 2 不同算法在各数据集上的精度比较(集成规模=10) Table 2 Accuracy values of the different algorithms on datasets (ensemble size=10) |
当集成的规模设置为40个,即DTELARS是从40个训练的决策树中进行选择和集成,Bagging和Boosting是分别地训练和使用40个决策树进行集成时,DTELARS在所有数据集上的平均分类精度也高于其它算法(表 3)。由DTELARS创建的集成中所使用决策树的数目仅是Bagging和Boosting使用数目的17.8% (7.1/40.0)。
| 表 3 不同算法在各数据集上的精度比较(集成规模=40) Table 3 Accuracy values of the different algorithms on datasets (ensemble size=40) |
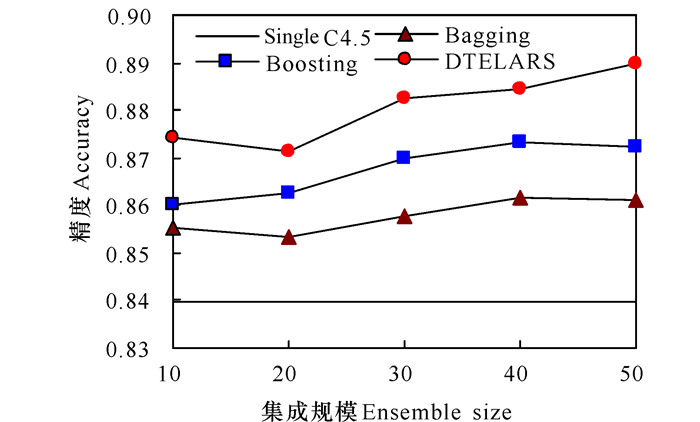
图 1展示了各种算法(包括单个决策树、DTELARS、Bagging和Boosting)在全部数据集上的平均分类精度随着集成规模的变化情况。注意在图中Bagging和Boosting是“全部集成”,因为它们对于横轴上标注的每一个数目而言都集成了全部的决策树。而单个决策树仅使用一个决策树进行分类,本文提出的算法DTELARS对于每个数目都是仅选择和使用一部分的决策树进行集成。
|
图 1 在全部数据集上不同算法的平均性能曲线 Fig.1 The average performance curves of different algorithms on datasets |
从图 1中可以得出以下结论:DTELARS在全部数据集上的平均分类精度始终高于单个决策树、Bagging和Boosting。
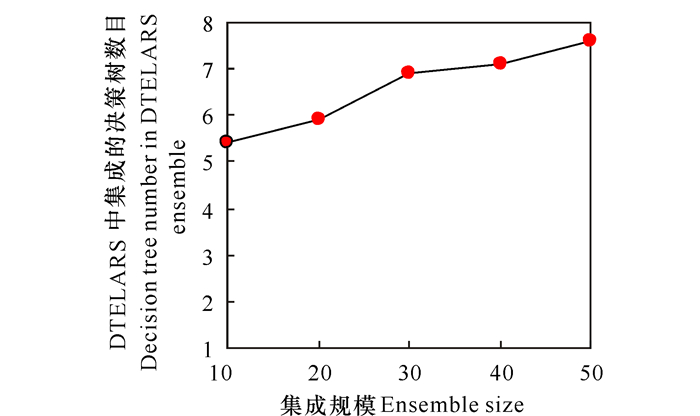
随着“全部集成”中决策树数目的增加,DTELARS所选择和集成的决策树只占全部决策树的一小部分;并且当“全部集成”中决策树的数目从10增加到50时,DTELARS所选择的决策树的数目只是缓慢地增加(图 2)。因此,DTELARS和“全部集成”的Bagging、Boosting相比,在存储开销和计算时间上都有显著的改善。
|
图 2 在全部数据集上DTELARS集成的平均决策树数目的变化曲线 Fig.2 The varying curve of average number of decision trees in the proposed algorithm on datasets |
为提高集成算法的泛化能力和效率,本文提出一种新的集成学习算法DTELARS。DTELARS基于粗糙集理论从训练的全部决策树中进行选择,只使用一部分决策树进行集成, 并与Bagging、Boosting、决策树算法在UCI数据集上进行性能比较。实验表明DTELARS不但减小集成规模,而且还获得更好的泛化能力。
| [1] |
DIETTERICH T G. Machine learning research:Four current directions[J]. AI Magazine, 1997, 18(4): 97-136. |
| [2] |
PAWLAK Z. Rough sets[J]. International Journal of Information and Computer Science, 1982, 11(5): 341-356. DOI:10.1007/BF01001956 |
| [3] |
顾翔元, 郭继昌, 田煜衡, 等. 基于条件互信息的空域隐写检测特征选择算法[J]. 天津大学学报:自然科学与工程技术版, 2017, 50(9): 961-966. GU X Y, GUO J C, TIAN Y H, et al. Spatial-domain steganalytic feature selection algorithm based on conditional mutual information[J]. Journal of Tianjin University:Science and Technology, 2017, 50(9): 961-966. |
| [4] |
SHI L, MA X, XI L, et al. Rough set and ensemble learning based semi-supervised algorithm for text classification[J]. Expert Systems with Applications, 2011, 38(5): 6300-6306. |
| [5] |
SHI L, DUAN Q, SI H, et al. Approach of hybrid soft computing for agricultural data classification[J]. International Journal of Agricultural and Biological Engineering, 2015, 8(6): 54-61. |
| [6] |
HONG Y H, XU S, LIANG J R. A model of classifier based on rough set and genetic neural network[J]. Guangxi Sciences, 2013, 20(2): 128-131, 136. |
| [7] |
樊艳英, 徐章艳, 张伟, 等. 一种基于粗糙集理论的值约简算法[J]. 广西科学院学报, 2013, 29(1): 4-6, 10. FAN Y Y, XU Z Y, ZHANG W, et al. A complete value reduction algorithm based on rough set theory[J]. Journal of Guangxi Academy of Sciences, 2013, 29(1): 4-6, 10. DOI:10.3969/j.issn.1002-7378.2013.01.002 |
| [8] |
BREIMAN L. Bagging predicators[J]. Machine Learning, 1996, 24(2): 123-140. |
| [9] |
FREUND Y, SHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139. |
| [10] |
CHOUCHOULAS A, SHEN Q. Rough set-aided keyword reduction for text categorization[J]. Applied Artificial Intell- igence, 2001, 15(9): 843-873. DOI:10.1080/088395101753210773 |
| [11] |
DUA D, KARRA T E.UCI machine learning repository[Z]. Irvine, CA: University of California, School of Information and Computer Science, 2017.http://archive.ics.uci.edu/ml.
|
| [12] |
YANG Y. An evaluation of statistical approaches to text categorization[J]. Journal of Information Retrieval(1), 1999, 69-90. |
| [13] |
QUINLAN J R. C4.5:Programs for machine learning[M]. San Francisco: Morgan Kaufmann Publishers, 1993.
|
 2018, Vol. 25
2018, Vol. 25 


