2. 广西师范大学物理科学与技术学院, 广西桂林 541004
2. College of Physics and Technology, Guangxi Normal University, Guilin, Guangxi, 541004, China
【研究意义】博弈现象在自然界和人类社会中普遍存在[1-2],博弈行为下合作的产生条件和能够维持的因素是目前研究的热点之一。到目前为止,演化博弈理论为解决合作问题提供了数学框架。例如,囚徒困境博弈和铲雪堆博弈作为点对交互(Pairwise interaction)形式解决了相应的合作问题而被广泛研究[3-10]。多人参与的公共品博弈呈现群体交互(Group interaction)形式,最近也受到广泛关注。【前人研究进展】公共物品博弈模型源于1968年英国Hardin的著作《公用地的悲剧》(The Tragedy of the Commons)[11],该著作将囚徒的困境和资源耗竭结合起来,描述了理性地追求最大化利益的个体行为是如何导致公共利益受损,如果人们只关注个人福利,公共资源就会被过度使用。现实社会中一些人总想享用别人的一部分劳动成果而自己却不愿意为此付出任何努力,这种社会现象普遍存在。所以,人们开始专注于公共物品的社会困境,此种困境通常被建模为公共物品博弈。在一个经典的公共物品博弈实验中[12],假设有1个公共的基金(Common pool),N个参与者独立并且同时决定选择投资(合作)或者不投资(背叛)到该基金中,合作者每次均投资1个单位的货币,背叛者投资为零,所投进的总资金将以r的倍数增值(r为增益系数,r>1),然后平分给所有个体。如果r < N,对于均匀混合的群体最终将全部是背叛者。现实社会中合作与背叛很好的共存的现象却普遍存在,Nowak等[4]将个体分布在二维方格网络上并提出空间结构能够促进合作,Hauert等[13]在此基础上,使所有个体参与以自身及其邻居为中心的群体博弈,每个群体的公共基金只平均给参与该群体博弈的个体。至今人们对空间公共物品博弈的研究已取得了丰硕的成果[14-24],如自愿参与[15-16]、惩罚[18-19]、反馈机制[20]、社会多样性[21]等。在以往的研究中策略更新规则是人们所关注的重点,参与者通过学习成功者的策略不断地调整自己的策略从而使自己利益最大化,这里的成功者指的是收益较大的个体。传统的公共物品博弈模型中,参与者在更新策略时只依据其邻居上一时步所得的收益,也就是说只参考其邻居最近一时步的收益情况,并不考虑更久之前的收益。在现实社会中,尤其是近年来,随着信息技术的迅速发展人们掌握各种信息的能力有了很大提高,为使自身利益最大化, 人们往往会参考周围邻居的行为,在做出决策前会考查对方过去投资所得的收益情况,并且对这些信息的记忆不会很快遗忘,所以有必要考虑收益的累积效应对公共物品博弈的影响。另外,历史的收益情况对博弈的影响会随时间的推移慢慢衰减,或说很早以前的经验对参与者来说其参考价值不大,因此收益累积长度是本文关注的重点。Wang等[25]提出了一种基于记忆机制的铲雪堆博弈模型,考察了记忆效应对二维周期边界条件的格子网络(四邻居和八邻居)及无标度网络上的铲雪堆博弈模型的作用,个体根据其邻居上一时步的策略进行反思,即选择自己的反策略做一次虚拟博弈并得到虚拟收益,再跟真实收益进行比较得到最佳策略,并更新记忆库,所以每个个体记忆中所记录的都是其历史时刻最佳的策略,研究结果表明合作水平随收益参数的变化呈现分段和非连续相变的现象。另外,Du等[26]和Wang等[27]研究了二维方格上基于记忆效应的囚徒困境博弈,通过定义一个记忆效应因子来控制参与者记忆历史收益能力的强弱,所得结果与铲雪堆博弈模型的结论类似。类似于记忆效应因子,Wang等[28]提出的改进型适度评价机制,通过可调的记忆强度来反映博弈者间的合作水平。所以, 记忆效应能够促进合作,但会受到收益参数的影响,也就是在不同的收益参数范围内记忆效应对博弈的合作行为的影响是不同的。【本研究切入点】在前人研究基础上,考察基于记忆效应的空间公共物品博弈模型,在该模型中参与者在学习邻居策略时不仅参考其上一时步的收益,而且参考前τ(τ≥1)时步的累积收益,即通过考察累积收益的方法来体现个体的记忆效应,在本文τ定义为收益累积长度。【拟解决的关键问题】基于累积收益,建立模型考察累积收益对系统的合作水平的影响。模拟结果表明,这种记忆效应对空间公共物品博弈合作行为的出现有重要影响,收益累积长度τ达到一定值时系统的合作水平将不再继续增大而是维持在某一稳定值。
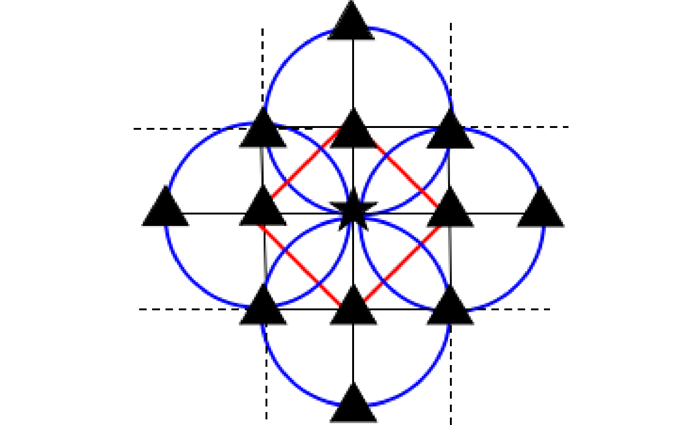
1 采用的模型及演化动力学选用的博弈模型为空间公共物品博弈,为了更直观地描述该博弈画出示意图,如图 1所示。
|
星形代表中心个体,三角形代表中心个体的邻居及其邻居的邻居 The star represents the center individual, the triangle represents the center of individual's neighbors and its neighbor's neighbors 图 1 公共物品博弈微观示意图 Fig.1 Microscopic diagram of public goods game |
个体仅和其最近邻进行公共物品博弈,每个个体参加以自己为中心和以其邻居为中心的群体博弈,即同时参与五个群体的博弈。每个群体增值后的总资金将平分给参与这个群体的所有个体,平分到的资金减去自身投资的金额为个体的净利润,称为收益。初始状态是合作者与背叛者均匀混合分布在这个群体中,每个个体以相等的概率选择合作策略或背叛策略。个体x参与一个群体博弈所得收益为
| ${p_\mathit{x}} = \left\{ \begin{array}{l} \frac{{r{n_c}}}{{{n_\mathit{c}} + {n_\mathit{d}}}} - 1{\rm{\;\;}}\mathit{if}{\rm{\;\;}}s\left( x \right) = C\\ \frac{{r{n_c}}}{{{n_\mathit{c}} + {n_\mathit{d}}}}{\rm{\;\;}}if{\rm{\;\;}}s\left( x \right) = D \end{array} \right., $ | (1) |
公式中,r表示增益系数,nc与nd分别代表该群体中在该时步选择合作和背叛的个体数(nc+nd=5),s(x)表示个体x的策略。每一时步个体x所得收益为
| $\begin{array}{l} W\left[ {s\left( y \right) \to s\left( x \right)} \right] = \\ \frac{1}{{1 + \exp \left\{ {\left[ {{P_\tau }\left( x \right) - {P_\tau }\left( y \right)} \right]/k} \right\}}}, \end{array} $ | (2) |
其中κ是噪声强度,在噪声强度很小(κ→0)的情况下,当Pτ(y)>Pτ(x)时学习概率为1;当Pτ(y)≤Pτ(x)时学习概率为0。意味着个体一定向比自己收益高的个体学习,当噪声强度取大于零的某一值时,即当所选邻居收益比自身收益小时仍以一定的概率学习其策略,这表示了该个体的非理性行为,并且κ值越大个体越不理性,本文中κ=0.5。Pτ(x)和Pτ(y)分别表示x和y两个参与者在距离现在最近的τ时步内的累积收益。当收益累积长度τ=t-1时表示参与者只参考上一时步的收益情况,此时该模型回归到经典的公共物品博弈模型;当收益累积长度τ=t-1时表示收益一直随时间累积,参与者的记忆效应也将不断积累,但参与者的记忆是有限的,在其有限记忆范围内,参与者必须通过各种渠道来掌握其邻居的收益情况然后跟自身的收益对比,最后做出决策,这显然要求参与者付出较大的代价才能做出较好的决策,结果自身收益并不一定达到最大值。所以,参与者能否通过参考其有限记忆范围内的一定时步的收益情况,然后做出决策并使其所得收益尽可能最大,以及通过累积收益的方法能否提高系统整体的合作水平,将是本文关注的重点。
在进行数值模拟前,考虑到收益要进行累加,这将最终导致公共物品的升值,从而使得货币贬值。为了抑制货币的贬值,需要对累积收益做归一化处理,此时的收益称为有效收益,归一化方法如下:
| ${P^\mathit{'}}_{i, t} = \frac{{c \times N}}{{\sum\limits_{n = 1}^N {{P_{n, t}}} }} \times {P_{i, t}}, $ | (3) |
其中,c表示参与者初始拥有资金数量,N表示参与者总个数。
2 数值模拟结果采用具有周期边界条件的二维方格网络模型,网络规模是由200×200个格点构成,每一个格点代表一个博弈参与者,每个参与者都有4个邻居。采用Monte-Carlo数值模拟方法,博弈开始每个参与者等概率的选择合作或背叛,即初始状态是合作者和背叛者均匀混合分布于网络中。参与者初始拥有相等数量c(这里c=5)的货币,选择合作的参与者每参与一个群体博弈投资1单位的货币,该时步同时参与了5个群体的博弈,因此合作者投资5单位货币,而选择背叛的参与者投资金额为零。
描述合作水平的物理量为合作频率ρc,指合作者所占的比例。在模拟中,研究的结果都是通过让系统演化2 000时步后取1 000步的数据,并且对50个不同初始合作者与背叛者分布状态做了平均而获得的,经验证演化2 000时步系统已达到动态平衡。
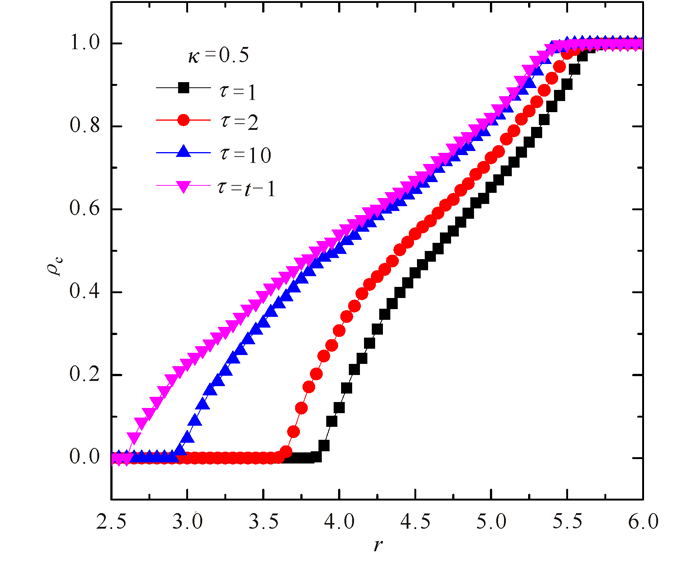
从图 2中可以看出收益累积长度越大即记忆效应越强,出现合作态所需增益系数的阈值越小,说明记忆效应促进了合作行为的出现。对于τ=1的情况是不考虑记忆效应,参与者根据最近一时步的收益情况来做出决策,在增益系数达到较大的值时才出现合作态;对于τ>1,增益系数较小时就出现了合作态,说明记忆效应促进合作行为的出现。
|
图 2 不同的收益累积长度τ下,合作频率ρc随增益系数r的变化情况 Fig.2 Different length of cumulative earnings τ, the va-riation of frequency of cooperation ρc with gain coefficient r |
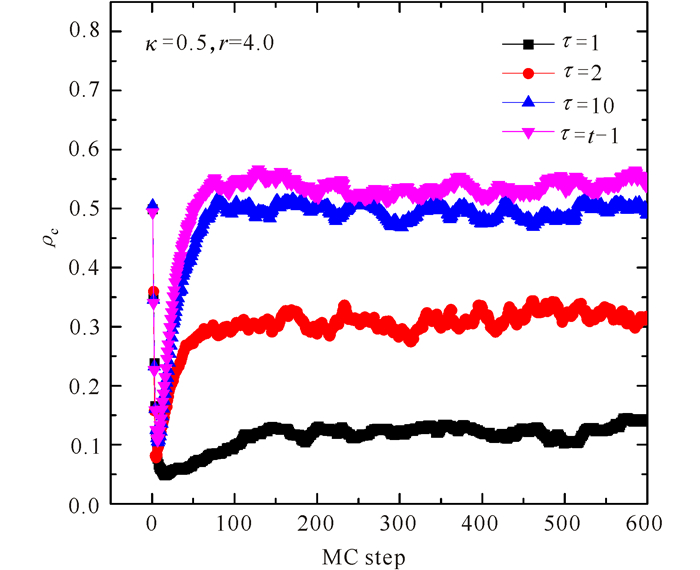
为了更好的理解记忆效应对合作行为的影响,需要对该模型进行了详细的动力学行为的研究。不同收益累积长度下合作频率随时间步数的变化情况如图 3所示。
|
图 3 不同收益累积长度τ下,合作频率ρc随时间步数的变化情况 Fig.3 Different length of cumulative earnings τ, the va-riation of frequency of cooperation ρc with time and steps |
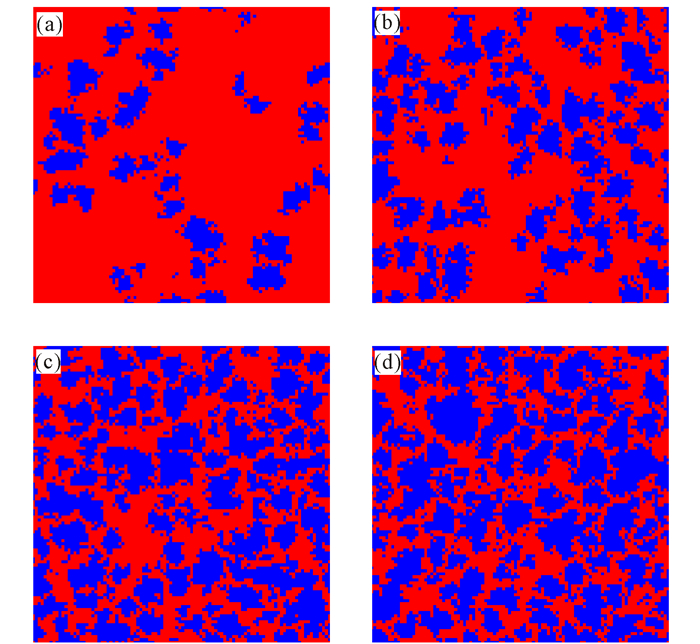
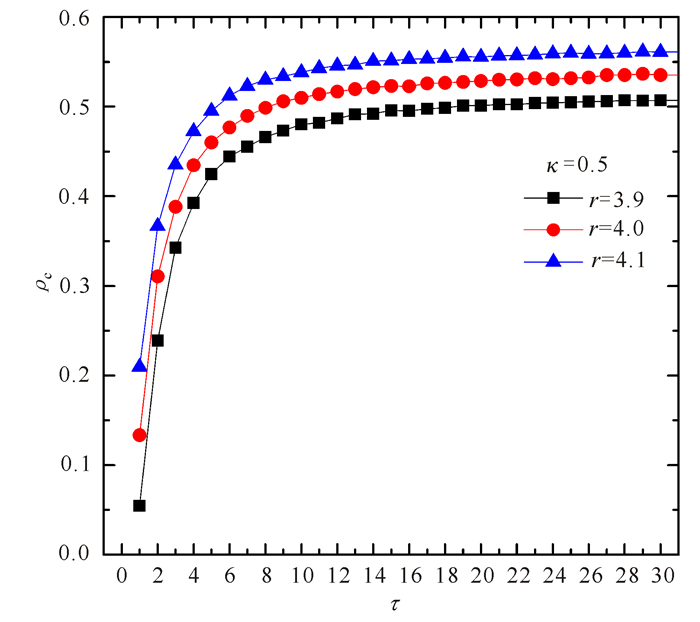
由于公共物品博弈模型中,参与者都会面临着搭便车的诱惑,即短期内不付出任何代价但却可以获得较高收益,因此合作率在短时间内会急剧下降,只有少数合作团簇幸存,而这些合作团簇边沿上的背叛者的收益比较小,这样背叛者又会学习其邻居的合作行为,于是合作率又逐渐增大,这与此前的关于合作者通过形成团簇存活下来的结论一致。另外,从图 3中还可以看出,对于τ=1,系统达到动态平衡所需时间较长而且平衡后合作率在一个较小的稳定值附近波动。当τ>1时系统达到平衡所需时间较短且平衡后合作率在较大的稳定值附近波动,τ越大系统达到平衡后的合作频率越高。下面是一组不同收益累积长度τ下系统达到动态平衡后某一时步的斑图快照(其中k=0.5, r=4.0),如图 4所示。
|
(a~d)分别对应收益累积长度τ为1,2,10和t-1的情况。红色表示背叛者,蓝色表示合作者 (a~d) represent the length of cumulative income is 1, 2, 10 and t-1, respectively.The red means betrayers and blue means collaborators 图 4 系统演化稳定后的斑图快照 Fig.4 The snapshot of pattern after the system evolves stably |
从斑图中可以看出,合作者通过形成团簇来抵御背叛者的侵入,这与空间囚徒困境博弈[4]的情况类似,这是由于空间效应引起的。但是,由于选择邻居时具有随机性所以斑图中合作团簇不是很规则。记忆效应越强,合作团簇的数目越多而且团簇大小也越大,Qin等[29]详细研究了合作团簇数目和大小对合作的影响,结果表明当合作者出现的时候,促进合作的关键因素不是合作团簇的数目而是合作团簇的大小。另外,从整体上看图 4c和图 4d图的斑图相似,而且图 3中也显示出当收益累积长度为10和t-1时合作频率随时间变化情况非常接近,即合作水平相当。因此设想是否可以通过累积有限长度的收益从而使得效果与最大限度的累积收益的效果相当。
接下来将模拟合作频率随收益累积长度的变化情况,试着寻找到最优的收益累积长度。图 5展示了在噪声强度k为0.5时,合作频率随收益累积长度的变化情况。
|
图 5 系统合作频率ρc随收益累积长度τ的变化情况 Fig.5 The variation of the frequency of system cooper-ation ρcwith the length of cumulative earnings τ |
从图 5中可以很明显的看出,在收益累积长度τ达到某一定值时系统的合作水平将不再增大而是维持在某一稳定值。同时,在收益累积长度τ相同的条件下,增益系数r越大,系统的合作频率ρc越大。
3 结论本文研究了记忆效应对空间公共物品博弈的影响,通过累积收益的方法使得参与者具有对历史收益的记忆,而且这个记忆库会随时间进行更新。定义了一个收益累积长度来表示参与者的记忆强度。研究结果表明,这种机制的引入促进了空间公共物品博弈合作行为的出现,而且存在一个最优的收益累积长度,使得系统合作水平达到最大。此模型结构简单、执行效率高、评价方法准确,能够给现实社会中的投资行为提供可靠的参考,可以大大降低投资行为的盲从性,提高理性投资,促进投资坏境的进一步发展。
| [1] |
徐许亮, 刘亮龙, 董荣胜. 激励Ad hoc网络自私节点协作的博弈论模型研究[J]. 广西科学院学报, 2008, 24(4): 300-302. XU X L, LIU L L, DONG R S. An incentive game theoretical mode of cooperation between selfish nodes in Ad hoc networks[J]. Journal of Guangxi Academy of Sciences, 2008, 24(4): 300-302. DOI:10.3969/j.issn.1002-7378.2008.04.007 |
| [2] |
白克钊, 蔡美静, 许志鹏, 等. 中心护栏对行人交通流的影响研究[J]. 广西科学, 2015(4): 368-372. BAI K Z, CAI M J, XU Z P, et al. Effect of central barrier on pedestrian traffic flow[J]. Guangxi Sciences, 2015(4): 368-372. DOI:10.3969/j.issn.1005-9164.2015.04.003 |
| [3] |
AXELROD R, HAMILTON W D. The evolution of cooperation[J]. Science, 1981, 211(4489): 1390-1396. DOI:10.1126/science.7466396 |
| [4] |
NOWAK M A, MAY R M. Evolutionary games and spatial chaos[J]. Nature, 1992, 359(6398): 826-829. DOI:10.1038/359826a0 |
| [5] |
HAUERT C, DOEBELI M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game[J]. Nature, 2004, 428(6983): 643-646. DOI:10.1038/nature02360 |
| [6] |
PANCHANATHAN K, BOYD R. Indirect reciprocity can stabilize cooperation without the secondorder free rider problem[J]. Nature, 2004, 432(7016): 499-502. DOI:10.1038/nature02978 |
| [7] |
SANTOS F C, PACHECO J M. Scalefree networks provide a unifying framework for the emergence of cooperation[J]. Physical Review Letters, 2005, 95(9): 098104. DOI:10.1103/PhysRevLett.95.098104 |
| [8] |
PONCELA J, GOMEZ-GARDENES J, FLORIA L M, et al. Robustness of cooperation in the evolutionary prisoner's dilemma on complex networks[J]. New Journal of Physics, 2007, 9(6): 281-289. |
| [9] |
RAND D G, CHRISTAKIS N A. Dynamic social net-works promote cooperation in experiments with humans[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(48): 19193-19198. DOI:10.1073/pnas.1108243108 |
| [10] |
CHEN X, SZOHNOKI A, PERC M, et al. Impact of generalized benefit functions on the evolution of cooperation in spatial public goods games with continuous strategies[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2012, 85(6 Pt 2)): 066133. |
| [11] |
HARDIN G. The tragedy of the commons.The population problem has no technical solution; it requires a fundamental extension in morality[J]. Science, 1968, 162(3859): 1243-1248. DOI:10.1126/science.162.3859.1243 |
| [12] |
HAUERT C, DE M S, HOFBAUER J, et al. Replicator dynamics for optional public good games[J]. Journal of Theoretical Biology, 2002, 218(2): 187-194. DOI:10.1006/jtbi.2002.3067 |
| [13] |
HAUERT C, SZABO G. Prisoner's dilemma and public goods games in different geometries:Compulsory versus voluntary interactions[J]. Complexity, 2010, 8(4): 31-38. |
| [14] |
HAUERT C, DE M S, HOFBAUER J, et al. Volunteering as Red Queen mechanism for cooperation in public goods games[J]. Science, 2002, 296(5570): 1129-1132. DOI:10.1126/science.1070582 |
| [15] |
SZABÍ G, HAUERT C. Phase transitions and volunteering in spatial public goods games[J]. Physical Review Letters, 2002, 89(11): 118101. DOI:10.1103/PhysRevLett.89.118101 |
| [16] |
XU Z, WANG Z, SONG H, et al. Selfadjusting rule in spatial voluntary public goods games[J]. Epl, 2010, 90(2): 20001. DOI:10.1209/0295-5075/90/20001 |
| [17] |
BRANDT H, HAUERT C, SIGMUND K. Punishment and reputation in spatial public goods games[J]. Proc Biol Sci, 2003, 270(1519): 1099-1104. DOI:10.1098/rspb.2003.2336 |
| [18] |
HELBING D, SZOLNKI A, PERC M, et al. Defectora-ccelerated cooperativeness and punishment in public goods games with mutations[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2010, 81(5 Pt 2): 561-578. |
| [19] |
SZOLNKI A, SZABO G, PERC M. Phase diagrams for the spatial public goods game with pool punishment[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2011, 83(3 Pt 2): 036101. |
| [20] |
RONG Z, YANG H X, WANG W X. Feedback reciprocity mechanism promotes the cooperation of highly clustered scalefree networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2010, 82(4 Pt 2): 047101. |
| [21] |
SANTOS F C, SANTOS M D, PACHECO J M. Social diversity promotes the emergence of cooperation in public goods games[J]. Nature, 2008, 454(7201): 213-216. DOI:10.1038/nature06940 |
| [22] |
JIANG L L, ZHAO M, YANG H X, et al. Reducing the heterogeneity of payoffs:An effective way to promote cooperation in the prisoner's dilemma game[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(3): 031144. |
| [23] |
SANTOS F C, PACHECO J M. Risk of collective failure provides an escape from the tragedy of the commons[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(26): 10421. DOI:10.1073/pnas.1015648108 |
| [24] |
APICELLA C L, MARLOWE F W, FOWLER J H, et al. Social networks and cooperation in hunter gatherers[J]. Nature, 2012, 481(7382): 497-501. DOI:10.1038/nature10736 |
| [25] |
WANG J, FU F, WU T, et al. Emergence of social cooperation in threshold public goods games with collectiverisk[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(2): 016101. |
| [26] |
DU J, WU B, WANG L. Evolution of global cooperation driven by risks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2012, 85(5 Pt 2): 056117. |
| [27] |
WANG W X, REN J, CHEN G, et al. Memory based snowdrift game on networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2006, 74(2): 056113. |
| [28] |
WANG J, LIU L N, DOMG E Z, et al. An improved fitness evaluation mechanism with memory in spatial prisoner's dilemma game on regular lattices[J]. Communications in Theoretical Physics, 2013, 59(3): 257-262. DOI:10.1088/0253-6102/59/3/02 |
| [29] |
QIN S M, CHEN Y, ZHAO X Y, et al. Effect of memory on the prisoner's dilemma game in a square lattice[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2008, 78(1): 041129. |
 2018, Vol. 25
2018, Vol. 25 


