2. 广西大学数学科学学院, 广西南宁 530004
2. College of Mathematics and Information Science, Guangxi University, Nanning, Guangxi, 530004, China
考虑非线性无约束最优化问题:
| $\min \left\{ {f\left( x \right)|x \in {R^n}} \right\}, $ | (1) |
其中目标函数f(x):Rn→R是连续可微非线性函数。共轭梯度法在计算过程中只需运用一阶导数信息,存储信息少,其收敛速度介于最速下降法和牛顿法之间,具有二次终止性,在求解非线性无约束优化问题时有良好的数值效果,而且编程简便,是最优化问题求解中最常用的方法之一,其迭代公式为
| ${x_{k + 1}} = {x_\mathit{k}} + {\mathit{\alpha }_\mathit{k}}{d_\mathit{k}}, k = 0, 1, 2, \cdots , $ |
xk+1和xk分别是第k+1次和第k次迭代点,αk是步长因子,dk是搜索方向,其迭代公式定义为
| ${d_{k + 1}} = \left\{ \begin{array}{l} - {g_{k + 1}}{\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;\;}}k = 0\\ - {g_{k + 1}} + {\mathit{\beta }_\mathit{k}}{\mathit{d}_k}{\rm{\;\;\;\;if\;\;k}} \ge {\rm{1}} \end{array} \right., $ | (2) |
其中参数βk∈R,gk+1是函数f(x)在点xk+1上的梯度函数。共轭梯度法主要考虑步长因子αk和搜索方向dk两个因素。众所周知,步长因子αk计算有精确线搜索和非精确线搜索两种方法,因为精确线搜索在计算过程中计算量太大,因此在实际计算中主要采用非精确线搜索。经典非精确线搜索方法有以下几种:弱Wolfe-Powell(WWP)线搜索[1],强Wolfe-Powell(SWP)线搜索[2],推广Wolfe-Powell线搜索[3],Armijo线搜索[4]和Grippo-Lucidi线搜索[5]等。研究表明,非精确线搜索的建立,需要考虑到两个问题[6]:满足非精确线搜索准则的αk是否存在,采用非精确线搜索准则的共轭梯度法是否全局收敛。在实际运算中,线搜索需要一定量的运算时间,而且线搜索的选择会影响到算法的计算效果。近来,针对于PRP共轭梯度法的线搜索研究取得了一些成果,较为典型的有韦增欣的3种新型线搜索[7-9],也已经得到广泛使用。
2017年,Yuan等[10]在其论著中提出一种新型线搜索(简称MWWP型线搜索),在较强的条件下该线搜索对经典PRP公式具有全局收敛的性质,数值实验结果表现很好,更具竞争性。MWWP型线搜索形式如下:
| $\begin{array}{l} {\rm{\;\;\;\;\;\;}}f\left( {{x_\mathit{k}} + {\alpha _k}{d_k}} \right) \le {f_\mathit{k}} + \mathit{\delta }{\alpha _\mathit{k}}g_k^T{d_\mathit{k}} + \\ {\mathit{\alpha }_\mathit{k}}\min \left[ { - {\delta _1}g_k^Tdlk, \delta \frac{{{\mathit{\alpha }_k}}}{2}{{\left\| {{d_\mathit{k}}} \right\|}^2}} \right] \end{array} $ | (3) |
和
| $g{\left( {{x_\mathit{k}} + {\alpha _k}{d_k}} \right)^T}{d_\mathit{k}} \ge \sigma g_k^T{d_\mathit{k}} + \min \left[ { - {\delta _1}g_k^T{d_\mathit{k}}, \delta {\alpha _k}{{\left\| {{d_\mathit{k}}} \right\|}^2}} \right], $ | (4) |
其中,δ∈(0, 1/2),δ1∈(0, δ)和σ∈(δ, 1)。
同样的,针对公式(2)参数βk选取不同的公式即为不同的方法,经典的有以下6种:FR、PRP、HS、LS、DY和CD等方法[11]。这些个方法各具特点,PRP、HS和LS方法数值好但在一般条件下不具备全局收敛性,FR、DY和CD方法理论上收敛性表现良好但是数值结果不是很理想,总体而言在数值结果上PRP方法表现最为优越。针对PRP共轭梯度法收敛性质差的缺陷,许多研究者通过修正PRP公式,在适当的线搜索上设计新的算法,取得丰富的成果。其中,黎勇[12]给出一种修正PRP共轭梯度法,其参数βk*形式如下:
| $\mathit{\beta }_k^* = \frac{{g_k^T\left( {\frac{{\left\| {{g_{k - 1}}} \right\|}}{{\left\| {{g_\mathit{k}}} \right\|}}{g_\mathit{k}} - {g_{k - 1}}} \right)}}{{g_{k - 1}^T{g_{k - 1}}}}, $ | (5) |
式(5)参数βk*具有非负性等性质,通过式(5)建立的共轭梯度法均具有较好的全局收敛性[12-14],在数值试验上针对选取的测试函数计算出的结果普遍良好且稳定[12-13],适合求解实际大规模非线性无约束最优化问题。
但是,式(5)在MWWP型线搜索下是否也具有全局收敛性质,数值结果表现如何等情况尚未提出。一个好的共轭梯度法通常与选定的线搜索有很大的关系,基于此,本文利用MWWP型线搜索和公式(5)设计一个新的算法,分析其全局收敛性,并分别采用其他经典的几类线搜索对公式(5)进行大规模问题的数值实验,分析新算法的有效性,最终通过对MWWP型线搜索和公式(5)的进一步研究,给大规模非线性无约束优化问题提供更好的解决方法。
1 新线搜索下修正PRP共轭梯度法为方便表述,本文将新算法称为算法1,其步骤如下。
步骤1:选择一个初始点x1∈Rn,ε∈(0, 1),δ∈(0, 1/2),δ1∈(0, δ), σ∈(δ, 1)。令d1=-g1=-▽f(x1), k=1;
步骤2:如果‖gk‖≤ε,则停止;
步骤3:利用线搜索(4)和(5)计算步长αk;
步骤4:令xk+1=xk+αkdk;
步骤5:如果‖gk+1‖≤ε,则停止;
步骤6:利用公式(3)计算参数βk*,公式(2)计算搜索方向dk+1=-gk+1+βk*dk;
步骤7:令k:=k+1,然后继续步骤2。
一般的,在非线性共轭梯度法收敛性的证明中需要用到以下假设。
假设1:
(A) 水平集L0={x|f(x)≤f(x0)|}有界,其中f(x0)是初始点。
(B) 令f(x)是连续可微,且梯度函数g(x)在水平集L0>0内Lipschitz连续,即
| $\left\| {g\left( x \right) - g\left( y \right)} \right\| \le L\left\| {x - y} \right\|, x, y \in {R^n}。$ | (6) |
因为{f(xk)}是单调递减序列,因此由算法产生的序列{xk}包含在水平集L0中,且存在一个常数XM>0,使得
| $\left\| x \right\| \le {X_M}, x \in {L_0}。$ | (7) |
Yuan等[10]指出,MWWP线搜索有两种情况:
① min(-δ1g(xk)Tdk, δαk‖dk‖2)=δαk‖dk‖2;
② min(-δ1g(xk)Tdk, δαk‖dk‖2)=-δ1g(xk)Tdk
本文主要讨论算法1在MWWP线搜索情况①条件下的全局收敛性。
为证明算法1的全局收敛性,下面给出假设2。
假设2:下面的关系式
| $d_k^T{g_\mathit{k}} < 0{\rm{\;\;和\;\;}}{{\rm{g}}_{k + 1}}{d_k} \le - {\sigma _1}g_k^T{d_\mathit{k}} $ | (8) |
对任意的k都成立,其中σ1≤σ。
以下我们将讨论新算法的全局收敛性。首先给出引理1和引理2,其具体的证明详见Yuan等[10]的Lemma 4.1和Lemma 4.2,本文不再赘述。
引理1 考虑算法1,且假设1和假设2成立,如果序列{xk, αk, dk, gk}由算法1生成,则下面两个式子必有一个成立:
| $\sum\limits_{k = 0}^\infty {\frac{{{{\left\| {{g_\mathit{k}}} \right\|}^4}}}{{{{\left\| {{d_\mathit{k}}} \right\|}^2}}}} < \infty $ | (9) |
或
| $\mathop {\lim }\limits_{x \to \infty } \inf \left\| {{g_\mathit{k}}} \right\| = 0。$ | (10) |
引理2 假设条件满足引理1,如果
| $\sum\limits_{k = 0}^\infty {\frac{1}{{{{\left\| {{d_\mathit{k}}} \right\|}^2}}}} < \infty , $ | (11) |
那么下式
| $\mathop {\lim }\limits_{x \to \infty } \inf \left\| {{g_\mathit{k}}} \right\| = 0 $ | (12) |
成立。
定理1 假设条件满足引理1,且MWWP线搜索满足情况①,即
| $\min \left( { - {\delta _1}g{{\left( {{x_\mathit{k}}} \right)}^T}{d_\mathit{k}}, \delta {\mathit{\alpha }_k}{{\left\| {{d_\mathit{k}}} \right\|}^2}} \right) = \mathit{\delta }{\mathit{\sigma }_\mathit{k}}{\left\| {{d_\mathit{k}}} \right\|^2}, $ |
那么有
| $\mathop {\lim }\limits_{x \to \infty } \inf \left\| {{g_\mathit{k}}} \right\| = 0。$ |
证明:采用反证法来证明。假设定理不成立,那么存在一个常数ε0>0,使得
| $\left\| {{g_k}} \right\| \ge {\varepsilon _0}, \forall \mathit{k} \ge {\rm{1}}{\rm{。}} $ |
由假设1,则存在一个常数GM>0,使得‖g(x)‖≤GM,x∈Rn,且dk+1=-gk+1+βkdk。于是有
| $\begin{array}{l} {\rm{\;\;\;\;}}\left\| {{d_{k + 1}}} \right\| \le \left\| { - {g_{k + 1}} + \mathit{\beta }_k^*{d_\mathit{k}}} \right\| \le \left\| {{g_{k + 1}}} \right\| + \\ \left\| {\beta _k^*} \right\|\left\| {{d_k}} \right\| \le \left\| {{g_{k + 1}}} \right\| + \\ \frac{{\left\| {g_{k + 1}^T} \right\|\left\| {\frac{{\left\| {{g_\mathit{k}}} \right\|}}{{\left\| {{g_{k + 1}}} \right\|}}{g_{k + 1}} - {g_\mathit{k}}} \right\|}}{{{{\left\| {{g_\mathit{k}}} \right\|}^2}}}\left\| {{d_\mathit{k}}} \right\| = \left\| {{g_{k + 1}}} \right\| + \\ \frac{{\left\| {g_{k + 1}^T} \right\|\left\| {\frac{{{g_\mathit{k}}}}{{{g_{k + 1}}}}{g_{k + 1}} - {g_{k + 1}} + {g_{k + 1}} - {g_k}} \right\|}}{{{{\left\| {{g_\mathit{k}}} \right\|}^2}}} \cdot \\ \left\| {{d_\mathit{k}}} \right\| \le \left\| {{g_{k + 1}}} \right\| + \\ \frac{{\left\| {g_{k + 1}^T} \right\|\left( {\left\| {\frac{{\left\| {{g_\mathit{k}}} \right\|}}{{\left\| {{g_{k + 1}}} \right\|}}{g_{k + 1}} - {g_{k + 1}}} \right\| + \left\| {{g_{k + 1}} - {g_k}} \right\|} \right)}}{{{{\left\| {{g_k}} \right\|}^2}}}\\ \left\| {{d_\mathit{k}}} \right\| \le \left\| {{g_{k + 1}}} \right\| + \\ \frac{{{{\left\| {g_{k + 1}^T} \right\|}^2}\left\| {{g_{k + 1}} - {g_k}} \right\|\left\| {} \right\|{d_k}}}{{{{\left\| {{g_k}} \right\|}^2}}} \le \\ \left\| {{g_{k + 1}}} \right\| + \frac{{2{G_M}L\left\| {{s_\mathit{k}}} \right\|\left\| {{d_\mathit{k}}} \right\|}}{{{{\left\| {{g_k}} \right\|}^2}}} \le \left\| {{g_{k + 1}}} \right\| + \\ \frac{{2{G_M}L\left\| {{s_k}} \right\|}}{{\mathit{\varepsilon }_0^2}}\left\| {{d_\mathit{k}}} \right\|, \end{array} $ |
又由式(3),得到
| $\begin{array}{l} {\rm{\;\;\;\;}}\mathit{f}\left( {{x_\mathit{k}}} \right) - f\left( {{x_\mathit{k}} + {\alpha _k} + {d_k}} \right) \ge - \delta {\alpha _k}g_k^T{d_k}\\ {\alpha _k}\min \left[ { - {\delta _1}g_k^T{d_k}, \mathit{\delta }\frac{{{\alpha _k}}}{2}{{\left\| {{d_k}} \right\|}^2}} \right] \ge - \left( {\mathit{\delta - }{\mathit{\delta }_1}} \right)g_k^T{d_k}。\end{array} $ |
对上述不等式从k=0到∞求和,结合假设1(A),得到
| $\sum\limits_{k = 0}^\infty {\left( { - {\delta _1}{\mathit{\alpha }_\mathit{k}}g_k^T{d_k}} \right)} < \infty 。$ | (13) |
由MWWP线搜索的情况①:min(-δ1g(xk)Tdk, δαk‖dk‖2)=δαk‖dk‖2和式(13),有
| $\begin{array}{l} \;\;\;\;\sum\limits_{k = 0}^\infty {\left( {\delta {{\left\| {{s_\mathit{k}}} \right\|}^2}} \right) = \sum\limits_{k = 0}^\infty {\left( {\mathit{\delta }\alpha _k^2{{\left\| {{d_\mathit{k}}} \right\|}^2}} \right)} } \le \\ \sum\limits_{k = 0}^\infty {\left( { - {\delta _1}{\alpha _k}g_k^T{d_k}} \right) < \infty 。} \end{array} $ |
则
| $\left\| {{s_\mathit{k}}} \right\| \to \infty , \mathit{k} \to \infty \mathit{。} $ |
从而,存在一个整数k0≥0和一个常数s∈(0, 1),对所有的k≥k0,使得
| $\frac{{2{G_M}L\left\| {{s_\mathit{k}}} \right\|}}{{\varepsilon _0^2}} \le s。$ |
因此,对所有的k≥k0,我们有
| $\left\| {{d_k}} \right\| \le {G_\mathit{M}}, \forall k > 0。$ |
这与引理2矛盾。证明完毕。
3 数值实验和新算法有效性分析为考查本文提出的新搜索下修正PRP共轭梯度法方法(算法1)的数值表现,下面我们将其与算法2、算法3和算法4进行比较。相关的参数选取分别如下。
算法1:公式(3)与MWWP线搜索[10],其中δ=0.49, δ1=0.24, σ=0.67;
算法2:公式(3)与弱Wolfe-Powell线搜索[1],其中δ=0.49, σ=0.67;
算法3:公式(3)与广义Wolfe-Powell线搜索[3],其中δ=0.49, σ1=0.67, σ1=11.12;
算法4:公式(3)与强Wolfe-Powell线搜索[2],其中δ =0.49, σ=0.67。
此次数值实验,选用Bongartz等[15]和Andrei[16]提出的CUTEr数据库中69个测试问题,分别对4种算法进行模拟试验。电脑系统为Intel(R)Xeon(R)CPU,E5507 @ 2.27 GHz,4.00 GB内存,Windows 7操作系统。采用MATLAB2014b编程和运行,维数取值为[4500, 9000, 15000, 45000],终止条件:‖gk‖≤10-5或迭代次数超过800。测试问题见表 1。
| 表 1 测试问题 Table 1 Test problem |
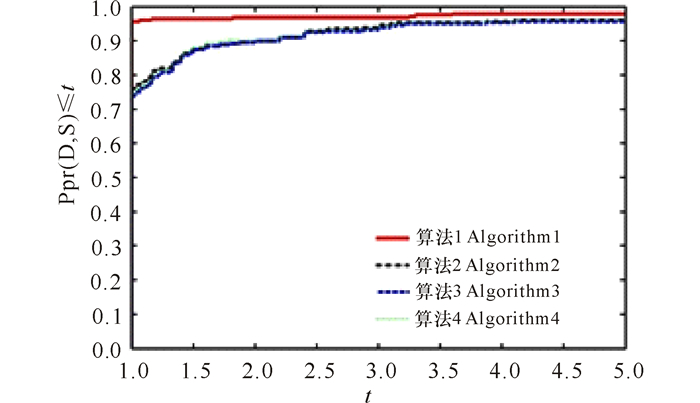
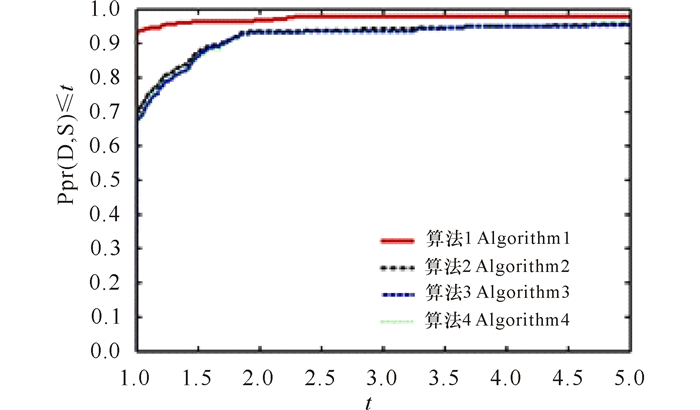
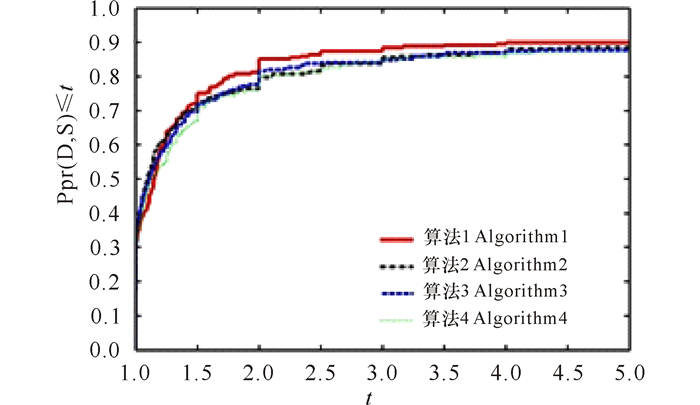
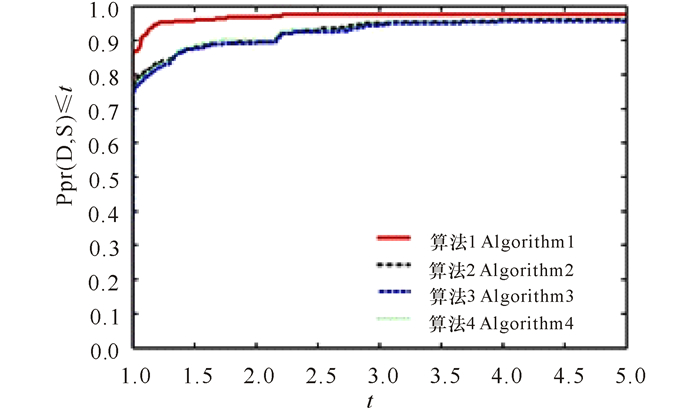
我们采用Dolan和Mor'e[17]提出的比较分析方法。根据本次实验的数值结果,针对4种算法的迭代次数(NI)、目标函数值计算次数(NF)、运行时间(CPUtime)和目标函数梯度计算次数(NG)等4个指标,分别作出算法1、算法2、算法3和算法4的性能比较图,详见图 1~4。从性能比较图的曲线变化走向可以看出,在相同的运行环境下,对选取的69个测试问题,算法1在迭代次数、目标函数值的计算次数、运行时间和目标函数梯度的计算次数上,都比算法2、算法3和算法4的计算效率更好,稳定性更优。
|
图 1 迭代次数比较图 Fig.1 Comparison graph of iteration number |
|
图 2 目标函数值计算次数比较图 Fig.2 Comparison graph of calculation number of objective function value |
|
图 3 运行时间比较图 Fig.3 Comparison graph of runing time |
|
图 4 目标函数梯度值计算次数比较图 Fig.4 Comparison graph of calculation number of objective function gradient value |
本文针对大规模非线性无约束优化问题,在经典非精确线搜索的基础上,利用Yuan等[10]提出的新型线搜索技术,结合黎勇[12]的修正PRP公式,设计出一种新的PRP共轭梯度法。在适当的条件下,证明新算法的全局收敛性。对选取的69个测试函数进行初步的数值试验,维数取值范围在[4500, 9000, 15000, 45000],并与3种经典非精确线搜索技术下的算法进行比较分析。结果表明,新算法能够有效求解45000维的大规模问题,总体表现更好,新算法是有效的。
在未来的工作中,我们将对新线索的理论进行思考和讨论,如新线索在其他共轭梯度法上的应用,新算法中相关参数选取对算法运行效果的影响;同时,新算法在解决实际大规模非线性无约束优化问题的效果有待进一步验证。
| [1] |
MCCORMICK G P. A modification of Armijo's step-size rule for negative curvature[J]. Mathematical Programming, 1977, 13(1): 111-115. DOI:10.1007/BF01584328 |
| [2] |
YUAN Y X, SUN W Y. Theory and methods of optimization[M]. Beijing: Science Press of China, 1999.
|
| [3] |
李董辉, 童小娇, 万中. 数值最优化[M]. 北京: 科学出版社, 2005. LI D H, TONG X J, WAN Z. Numerical optimization[M]. Beijing: Science Press, 2005. |
| [4] |
ARMIJO L. Minimization of functions having lipschitz conditions partial derivatives[J]. Pacific Journal of Mathematics, 1966, 16(1): 1-3. DOI:10.2140/pjm |
| [5] |
GRIPPO L, LAMPARIELLO F, LUCIDI S. A nonmon-otone line search technique for Newton's methods[J]. SIAM J Numer Anal, 1986, 23(4): 707-716. DOI:10.1137/0723046 |
| [6] |
高立. 数值最优化方法[M]. 北京: 北京大学出版社, 2014. GAO L. Numerical optimization method[M]. Beijing: Peking University Press, 2014. |
| [7] |
WEI Z X, LI G Y, QI L Q. Global convergence of the Polak-Ribière-Polyak conjugate gradient method with an Armijo-type inexact line search for nonconvex unconstrained optimization problems[J]. Mathematics of Computation, 2008, 77: 2173-2193. DOI:10.1090/S0025-5718-08-02031-0 |
| [8] |
WEI Z X, QI L Q, CHEN X. An SQP-type method and its application in stochastic programs[J]. Journal of Optimization Theory and Applications, 2003, 116(1): 205-228. DOI:10.1023/A:1022122521816 |
| [9] |
WEI Z X, QI L Q, ITO S. New step-size rules for optimization problems[J]. International Conference on Recent Advances in Computational Mathematics, Japan SIAM, 2001. |
| [10] |
YUAN G L, WEI Z X, LU X W. Global convergence of BFGS and PRP methods under a modified weak Wolfe-Powell line search[J]. Applied Mathematical Modelling, 2017, 47: 811-825. DOI:10.1016/j.apm.2017.02.008 |
| [11] |
戴彧虹, 袁亚湘. 非线性共轭梯度法[M]. 上海: 上海科学技术出版社, 2000. DAI Y H, YUAN Y X. Nonlinear conjugate gradient method[M]. Shanghai: Shanghai Scientific & Technical Publishers, 2000. |
| [12] |
黎勇. 一类修正PRP共轭梯度法的全局收敛性及其数值试验结果[J]. 西南大学学报:自然科学版, 2011, 33(11): 23-28. LI Y. Global convergence and numerical experiments of some new modification of PRP conjugate gradient method[J]. Journal of Southwest University:Natural Science, 2011, 33(11): 23-28. |
| [13] |
黎勇. 一种修改的PRP共轭梯度法[J]. 广西科学, 2013, 20(1): 5-8. LI Y. A modification PRP conjugate gradient method[J]. Guangxi Sciences, 2013, 20(1): 5-8. DOI:10.3969/j.issn.1005-9164.2013.01.002 |
| [14] |
黎勇. 无约束优化中的一种修正的PRP共轭梯度法的全局收敛性分析[J]. 百色学院学报, 2010, 23(3): 55-59. LI Y. Global convergence analysis of a modification PRP conjugate gradient method for unconstrained optimization[J]. Journal of Baise University, 2010, 23(3): 55-59. DOI:10.3969/j.issn.1673-8233.2010.03.010 |
| [15] |
BONGARTZ I, CONN A R, GOUNLD N. CUTE:Constrained and unconstrained testing environment[J]. Acm Transactions on Mathematical Software, 1995, 21(1): 123-160. DOI:10.1145/200979.201043 |
| [16] |
ANDREI N. An unconstrained optimization test functions collection[J]. Environmental Science and Technology, 2008, 10(1): 6552-6558. |
| [17] |
DOLAN E D, MORÉ J J. Benchmarking optimization software with performance profiles[J]. Mathematical Programming, 2001, 91(2): 201-213. |
 2018, Vol. 25
2018, Vol. 25 

