2. 广西大学计算机与电子信息学院, 广西南宁 530004;
3. 广西电网公司, 广西南宁 530004
2. School of Computer, Electronics and Information, Guangxi University, Nanning, Guangxi, 530004, China;
3. China Southern Power Grid, Nanning, Guangxi, 530004, China
能量收集网络(Energy harvesting network, EHN)[1-2]是一种节点自带能量收集装置的网络,能够通过收集环境中的太阳、风、震动、热量、电磁波、室内光等能量[3-4],将其转化成可用的电能,作为主要或辅助的电源供给无线设备完成网络通信任务。EHN融合可再生能源,降低传统能源的消耗并减少传统能源制造过程中产生的有害物质。同时对于能量受限型网络节点,EHN能够降低其死亡概率,当节点收集足够的能量时节点即可“重生”。EHN提高了节点的自治能力,拓宽了网络的部署范围,延长了设备的生命周期,为网络设备的永久运行提供了可能性。EHN广泛应用于节能型基站建设、高空无人机网络、无线传感网络、体域网等场景中。
然而,较传统的无线网络而言,EHN的发展研究仍存在诸多挑战。首先,传统的无线网络模型由于未考虑能量的随机性、瞬时性、记忆性以及有限性,因此并不能很好地适用于EHN。能量收集的不确定性导致其速率难以预知,继而难以解决网络节点的功率分配问题;同时由于不同设备、应用、网络密度、协议策略等因素的存在,建立准确的能量收集模型是进行网络部署、策略制定、系统规划以及应用设计等必不可少的过程。其次,EHN的系统运行规划更加复杂,需综合考虑系统能量收集状态、网络节点设备状态、通信环境等前提下,在能量收集、能耗均衡、吞吐量、安全速率等约束下实现系统性能与能耗之间以及能量传输与信息传输之间的均衡。再者,EHN中存在能量与负载分布不均的问题,因此在节点间实现能量与信息的联合传输,对于提高网络资源复用率、延长网络系统生命周期是十分重要的。基于无线信息与能量同步传输(Simultaneous wireless information and power transfer, SWIPT)和无线供电通信网络(Wireless powered communication network, WPCN)技术可以实现EHN网络中能量与信息的联合传输,建立准确的系统模型并求解最优能量与信息协方差矩阵,因此成为当前EHN的热门问题。
本文将介绍EHN的信息论基础和建模方法,重点从信息论视角、能量收集模型、离线与在线能量规划、无线能量与信息联合传输等4个方面阐述EHN领域近几年的技术研究现状与发展趋势。
1 能量收集网络的信息论基础考虑经典的加性高斯白噪声(Additive white gaussian noise, AWGN)信道,输入X,加性零均值单位方差的高斯噪声N,输出Y=X+N。此时信道的容量为C=0.5log2(1+P)。基于香农定理,码字平均功率约束如下:
| $ \frac{1}{n}\sum\limits_{i=1}^{n}{{}}\text{ }X_{i}^{2}\le P。$ | (1) |
对于非常大的n值,Xi表示传输码字的第i个元素。而当将发送端的能量收集视为平稳遍历随机过程Ei时,则其平均充电速率
| $ \sum\limits_{i=1}^{k}{{}}\text{ }X_{i}^{2}\le \sum\limits_{i=1}^{k}{{}}{{E}_{i}}, k=1, \ldots , n。$ | (2) |

|
| 图 1 随机能量到达的AWGN信道示意图 Fig. 1 Schematic diagram of AWGN channel with random energy arrival |
另一方面,当设备不配备电池时,码字约束为
| $ X_{i}^{2}\le {{E}_{i}}, i=1, \ldots , n, $ | (3) |
该式又称为瞬时随机幅值约束,如图 1b所示。而当电池容量有限(最大容量Emax)时,则电池中的电量
| $ {{B}_{i+1}}=\text{min}\left\{ {{B}_{i}}-X_{i}^{2}+{{E}_{i}}, {{E}_{\text{max}}} \right\}。$ | (4) |
二进制无噪声链路下能量收集信道的容量已在3种情形下计算得出,这3种情形分别是无限容量电池(Emax=∞)[5]、无电池(Emax=0)[6]和单位容量电池(Emax=1)[7]。本节回顾信息论视角下,能量收集对网路信道容量的影响,总结EHN中信道容量的证明及其实现方法。
1.1 无限容量电池的信道容量首先每个码字满足约束式(2),同时依据大数定理满足平均功率约束式(1),即
Ozel等[5]给出了两种实现上界的方式。一种是存储再发送策略,发送端在起初的h(n)信道使用中存储能量,继而在剩余n-h(n)的信道使用中依据码本传输数据,该码本依据对功率的独立同分布高斯采样生成,等于平均充电速率P。令h(n)和n-h(n)均趋于∞,选取h(n)满足o(n),如h(n)≈log2(n),继而可以实现AWGN容量。这一过程可以看作:通过在存储阶段收集无限的能量,将数据发送阶段的能量耗尽概率视作0,同时通过选择h(n)~o(n)使得在存储阶段不传输任何数据。另一种策略是最佳传输策略,即数据传输在能量到达时立即进行,无须经历存储阶段。此时高斯码本依据平均功率ε建立,ε的值小于平均充电速率。
1.2 无电池的信道容量考虑无电池的情况,此时,信道输入为式(3)所示的瞬时幅值约束。然而,这种幅值约束是时变和随机的。发送端通常知道能量到达过程,接收端则不知。因此发送端依据所观测到的系统能量状态来选择码符。Ozel等[5]归纳了Smith等[8]考虑静态幅值约束AWGN信道和Shannin[9]考虑状态独立信道的容量,计算了无电池情形下的信道模型容量。结论指出,发送端在能量到达状态为e1时发送信道输入T1,在能量到达状态为e2时发送信道输入T2,其中T1和T2是满足
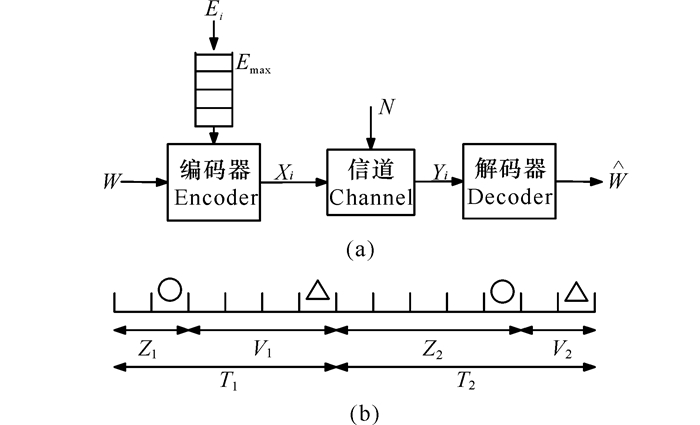
对于有限容量的电池,如图 2a所示,信道输入受到当前电池中能量的瞬时幅值约束。Ozel等[6]和Smith等[8]指出,当信道输入为高斯信道下的连续幅值约束或独立同分布的随机幅值约束时,最优输入分布是离散的。然而,这种离散的质点是任意的实数,即跟踪能量序列的动态特性很困难。
对于可跟踪的抽象系统,Tutumcuoglu等[7]将能量到达过程模拟为定量的数乘,继而考虑基于该定量的物理层离散码表,研究假设物理层是无噪声二值信道,能量到达是二值的且电池为单位容量,即使在如此简单的模型中,接收端对电池状态的未知、电池状态的时效性以及电池状态的估计精度,均使得问题难以求解。Tutuncuoglu等[7]的研究结果表明这种单位电池的无噪声二值信道等价于文献[11]中的时变信道。这种等价将问题转换为加性几何噪声的时变信道优化问题,如图 2b所示,圆圈代表收集的能量,三角形代表向信道输入1。这里,当发送一个1后,需要等待一个随机的信道使用周期Zi以收集一个单位的能量进入电池;之后,等待Vi个信道周期以发送数据。其中Vi作为信道输入之一是一个待优化的变量。此时香农策略[9]是最优的。
|
| 图 2 有限容量电池系统(a)和等效时间序列(b) Fig. 2 Limited capacity battery system (a) and equivalent time series (b) |
2 能量收集网络模型
能量收集模型的研究主要分为基于概率论模型和非概率论模型两类。概率论模型含有对系统能量收集的先验知识,主要以马尔科夫链设计为主;非概率论模型则依据具体应用环境使用混合型的建模方法。
2.1 基于概率论的模型能量收集过程具有随机性,因此常用的建模过程为基于概率论的方法,通过先验知识对能量收集随机性进行评估,继而基于马尔科夫链建立能量收集模型。Kong等[12]尝试使用2N-状态的马尔科夫链,建立能量收集无线传感器网络中能量与事件感知流量的模型。其模型包含了能量收集可用和不可用两种状态,同时设定事件发生的概率。此方法的缺点在于当能量耗尽时事件感知概率、报告失败概率以及状态转移的平均到达时间难以估计。Kim等[13]使用了类似的方法,依据可传输任务量以及终止节点答复信息,使用马尔科夫链模拟电池剩余电量状态演变。基于能量和信道状态推算数据包发送失败的概率,进而分析系统通信的性能。
不同于上述时间分段方法,Liu等[14]使用时间连续的马尔科夫链模拟能量收集传感器网络中的能量存储设备和数据流。状态转移使用不同的能量收集概率、电池更换概率以及数据流产生概率表示,每一种概率均服从泊松分布。这种模型可以拓展为马尔科夫决策过程:每一个被传输的数据包都有一个“信息权重”,该值是与数据相关的价值函数。基于信息权重阈值,决定是否发送数据。
Ho等[15]考虑建立能量收集装置的模型,通过实验数据表明能量收集过程为一非平稳马尔科夫过程,指出当前研究大多假设其为平稳过程是不准确的,并强调建立非平稳过程的广义模型的重要性。为了便于分析,该模型基于能量收集状态的平稳马尔科夫链,其约束条件为含有“场景”参数的另一个平稳马尔科夫过程。由于马尔科夫链是该模型的一个特例,因此模型是广义的。将该模型在使用贝叶斯信息准则的能量收集设备中进行稳定性测试,结果表明该广义模型更适合描述震动能量的收集,而普通的平稳模型适合描述太阳能收集系统。Zou等[16]同样基于实验数据,尝试使用曲线拟合的方法建立能量收集模型,提供了不同的历史数据统计模型的拟合度结果。假设能量收集节点只能在时段起始阶段电池拥有足够的能量时才进行数据传输,分别采用离散均匀分布、几何分布、泊松分布以及变型的几何泊松分布进行分析研究,结果表明任意变型的泊松分布更好地匹配了历史数据。
2.2 基于非概率论模型能量收集模型的建立,除了使用马尔科夫链,还有许多其他类型的建模技术,用以为系统设计提供参考。Valera等[17]提出一种漏桶模型和相应的最小流约束方法,漏桶模型类似于排队系统中的令牌桶模型,适用于收集能量的最大流约束;而最小流约束方法用于模拟设备中剩余的不可用的能量,该方法与系统的功率消耗特性结合起来,可用于能量存储装置的设计,以及结合瞬时功率决定能量收集器的容量。
Part等[18]提出一种包含无线衰减信道和太阳辐射模型的复合型模型,光伏单元和电池的模型反映了能量收集传感器节点或网状网节点的无线和能量状态。该模型也可以用来测试系统性能,如丢包率和阻塞率、睡眠概率、平均延迟和队列长度、队列吞吐量和平均电池容量。Misra等[19]提出一种嵌套的层次模型用以描述能量收集系统的功能。模型包含能量存储层、存储接入层、功率控制层、功率转换层和设备测量层。为了方便能量与功率的感知操作,层与层之间增加了信息流和控制流。该模型可用于指导能量收集系统中元器件的选择。同时,在给定的能量收集系统中,该模型也可用于分析如何提高系统效率。
不同于上述研究,王哲等[20]提出一种基于场景生成的能量收集模拟技术。该方法基于历史能量获取数据,首先使用最优消减技术生成单时段代表场景,继而利用时齐模拟退火算法生成日场景序列,以准确模拟EHN中能量获取的随机特性。目前EHN模型的建立依赖于系统先验知识,对能量收集的准确估计成为系统能否有效运行的关键。
3 吞吐量最大化的离线能量管理策略本节考虑基于单用户信道和多用户信道下的能量收集通信问题,同时引入处理能耗与电池的不完美特性,求解EHN系统最优离线能量管理策略。
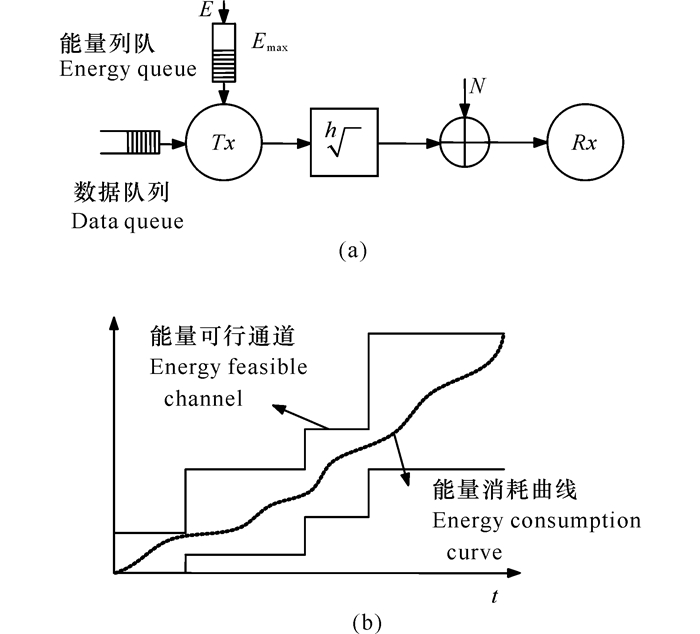
3.1 单用户信道考虑如图 3a所示的加性高斯噪声的单用户衰减信道。发送端有两个序列,数据序列用于存储等待发送的数据包,而能量序列存储收集的能量。此时的系统目标是使用电池中的能量合理规划数据包的传输。
Yang等[21]和Tutuncuoglu等[22]指出最优化问题的约束条件应包括收集能量的因果约束和电池有限容量约束。能量因果约束限制了未到达的能量不能够被系统利用,而有限容量约束要求能量到达时应无能量浪费。假设能量收集序列为{E0, E1, …, EN-1},时段长度为{l0, l1, …, lN-1}。由于速率-能量函数的凹性,能量收集过程中的功率必须保持连续[21]。这将功率控制策略简化为一个连续功率序列{P0, P1, …, PN-1}。能量因果约束[21]变为
| $ \sum\limits_{i=1}^{k}{{}}\text{ }{{l}_{i}}{{p}_{i}}\le \sum\limits_{i=1}^{k-1}{{}}\text{ }{{E}_{i}}, k=1, \ldots , N, $ | (5) |
|
| 图 3 能量收集系统(a)和能量可行性通道(b) Fig. 3 Energy harvesting system (a) and energy feasible channel (b) |
同时,无能量溢出约束[22]变为
| $ \sum\limits_{i=1}^{k}{{}}\text{ }{{E}_{i}}-\sum\limits_{i=1}^{k}{{}}\text{ }{{l}_{i}}{{p}_{i}}\le {{E}_{\text{max}}}, k=1, \ldots , N-1。$ | (6) |
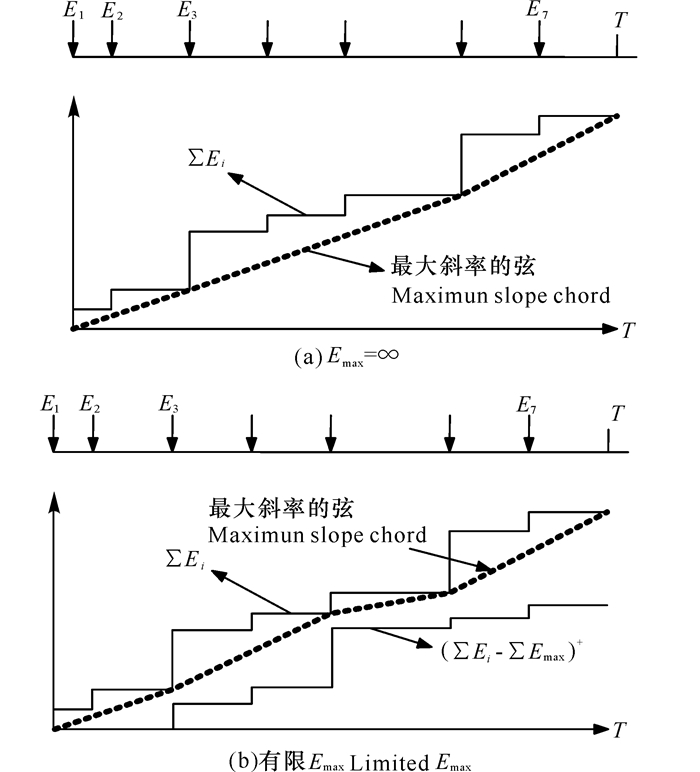
这两种约束可在图 3b中得到验证,阶梯上界为累积到达的能量,为能量因果约束提供了上确界,阶梯下界为无能量约束提供下确界曲线。任何可行的能量消耗曲线均落在这两条阶梯之间。Yang等[21]和Tutuncuoglu等[22]的研究表明,最优策略是能量可行通道内最大斜率的弦。这一策略的目标是保持最长的连续的功率消耗周期,同时保证无能量溢出。图 4a所示为Emax=∞情形下的一种能量最优消耗曲线,图 4b所示为有限Emax情形下的能量最优消耗曲线。
|
| 图 4 最优策略是连接两点之间的斜率最大的弦 Fig. 4 The optimal strategy is to connent the chord with the largest slope between the two points |
另一种对可行通道的逼近方法是定向注水算法[23],其目的是依据时间平均分配水量(即能量),此时能量因果约束提供了水流的方向。由于能量因果约束的存在,能量能够存储并在未来时段中使用,未来时段中收集到的能量不能够在当前时段中使用。基于凸优化问题中的Karush-kuhn-tucker (KKT)最优条件[23]
| $ p_{i}^{opt}=\frac{1}{\left( \sum\limits_{\text{ }j=i\text{ }}^{N+1}{{{\lambda }_{j}}-\sum\limits_{\text{ }j=i\text{ }}^{N}{{}}\text{ }{{\mu }_{j}}} \right)~}-1, i=1, \ldots , N, $ | (7) |
其中λj是能量因果关系的拉格朗日乘数,μj是无能量溢出约束的拉格朗日乘数。在定向注水算法中,首先水龙头是关闭的,不允许从一个水池向另一个水池流动;继而水龙头一个接一个打开,最多有(Emax-Ei)单位的能量从过去的水池传递到第(i+1)个水池。Ho等[24]则使用梯形注水算法求解该问题。
3.2 多用户信道Yang等[25]和Ozel等[26]的研究表明:在EHN的广播信道中,最优总传输功率管理策略与前文所述最优单用户情形下的最优策略相同。Antepli等[27]提出一种近似的广播信道算法求解多用户问题。Ozel等[28]将Antepli等[27]的算法拓展至衰减的多输入多输出(Multiple-input multiple-output, MIMO)信道中。在EHN的多址接入信道中,Yang等[29]使用一种组合的定向注水算法,该算法包括广义的注水算法[30]和迭代注水算法[31],最大化给定时段内的数据发送量,以此实现最优的能量管理。对于干扰信道,Tutuncuoglu等[32]针对两用户干扰信道,提出发送端的总速率最优传输策略。根据总速率表达式的凹性,使用定向迭代注水算法,即可获得总速率最优传输策略,其中单一用户的功率情况决定了其他用户的噪声等级。
Gunduz等[33]和Huang等[34]考虑全双工的端到端通信的双跳中继信道,源点和中继节点从大自然中收集能量。结果表明最优策略并不唯一,且存在分布式的最优方案,即源点不考虑中继节点能量收集特性,仅优化自身吞吐量,而中继节点仅依据自身能量特性和源点发送的数据优化自身吞吐量。Orhan等[35]、Tutuncuoglu等[36]和Varan等[37]将该问题拓展到半双工双跳和广义双中继的EHN中。Orhan等[38]和Xu等[39]在原有研究的基础上,增加考虑系统的处理能耗,基于能量因果约束、无能量溢出约束和处理损耗约束求取最大化的吞吐量。求解过程使用定向浇灌算法,收集到的能量首先分配到相应的池中,然后能量向右流动直至达到均衡状态。Orhan等[40]对其之前的工作[38]进行了拓展,考虑处理能耗的宽带衰减能量收集通信系统,研究结果表明:当能量受限时,附加带宽无法被利用。
4 系统效益最大化的在线能量管理假设时间分段且数据分段,即一个时段下数据仅有发送或丢弃两种状态,在线能量管理的目标是依据某些传输策略,实现EHN效益最大化。其中设备完全运行在在线状态,且能够获取常用的系统信息。此时,设备必须能够做出智能的选择,即基于当前系统状态(如电池中剩余电量或能量收集过程状况)判断是否发送数据。
4.1 完美电池状态信息下的最优传输策略假设系统能够完美估计当前电池剩余电量信息,目前人们提出了两种不同的模型。Michelusi等[41]给出了第一种模型,模型中每个数据包均配有相应的随机权重值Vk,代表当前数据包一旦被发送所能收获的系统效益。可以通过简单的阈值策略实现系统决策。每一时段内的平均效益可表示为式(8),其中Qk为能量到达序列。
| $ R=\underset{K\to \infty }{\mathop{\text{lim}\ \text{inf}~}}\, \frac{1}{K}\text{ }E\left[ \sum\limits_{k=0}^{K}{{{Q}_{k}}{{V}_{k}}} \right]。$ | (8) |
最优传输策略可通过诸如策略迭代算法(Policy iteration method, PIA)等标准数值方法求解[42]。同时,某些启发式算法如均衡法也能够有效地逼近Emax→∞时的最优解。其中阈值的设置原则是每个时段内的平均消耗能量等于预测收集的能量。
第二种模型中,数据传输所使用的不同功率等级将实现不同的系统效益,此时模型无须考虑权重值。Bertsekas[42]指出,该模型更接近真实情况,且能够扩展至能量收集过程互相关的情形中。如果能量收集过程依据隐性马尔科夫链自相关,则系统可使用之前所介绍的相同的策略,此时标准数值求解方法依旧适用,但是所增加的算法复杂度可能使其很难得到最优解的闭式表达式。研究结论表明,这种模型下系统性能不再单独受限于电池电量,同时也依赖于能量的动态收集过程,如对于较慢的能量收集过程,较大容量的电池有助于实现更好的系统收益。王哲等[43]提出能量收集网络节点能量收集可靠性定义,对节点能量收集的置信程度给出了评价,并基于不确定理论对能量收集的可靠性进行评估分析,分别建立节点无电池和无限容量电池情况下的可靠性模型。在此基础上提出能量收集可靠性多层不确定规划模型并对模型进行求解,接着提出一种在线能量平均分配算法,并从理论上证明算法竞争比的上界。最后,以实际的风电数据为例验证所提模型和方法的可行性和有效性。
4.2 不完美电池状态信息下的最优传输策略通常情况下,微处理器能够读取电池中剩余电量信息,但研究表明该过程是不准确的,如系统元器件参数的不确定性可能导致其读取误差接近30%[44]。同时,在获取电池电量数据的准确度与系统能量消耗之间存在均衡关系。因此,有必要考虑不确定电池状态信息下的系统最优传输策略。
此时依旧可以使用马尔科夫链模拟这种隐性过程,但马尔科夫链的状态信息有误差,因此马尔科夫决策过程不能够求解。该问题属于部分可观测马尔科夫决策领域。求解最优策略需要已知所有的历史信息,这使得该问题的求解过程极为困难。Michelusi等[45]指出求取该问题的次优解同样能够获得不错的系统收益,且次优解非常接近真实的最优解。Michelusi等[46]则指出,对于互相关的能量收集过程,设法获取能量收集过程比获取能量状态信息更为重要。
另一方面,能量收集过程的研究忽略了一个重要的问题,即电池在经历一定次数的充电后,其总容量会下降且放电速率增快。这种问题也常常出现在手机用户中。为了研究电池的降解现象,依旧可以使用马尔科夫决策过程(Markov decision process, MDP)建模,但需要增加记忆层用于描述电池随时间的降解现象。通常情况,在电池完成一定次数的充放电循环后,设置某个不大于1的系数表征电池总量的降解。另一种方法是使用概率模型进行模拟,先初始化不同级别的降解等级,电池在每个时段中,以一定的概率(该概率值很小)从一个等级下降到下一等级。Michelusi等[47]详述了这种建模方法,在保持模型容许复杂度的前提下详细研究了电池的降解现象,描述了电池在整个生命周期内每次充放电循环中能够提供的总能量。
5 无线能量与信息的联合传输前面讨论了EHN从外界收集能量的情况。为了增加EHN的资源复用率,可以考虑在其信息传输的同时实现能量的传输。本节将介绍EHN中能量与信息传输的研究现状。
5.1 信息论视角从交流信号中获取能量的可能性在电路研究的文献中有许多讨论,如基于生物医学植入领域[48]。Nintanavongsa等[49]首次给出了从交流信号中收集能量的信息论公式,Wang等[50]则研究了在接收功率约束下的信道容量问题。在最小的接收功率约束下,Nintanavongsa等[49]针对最大化互信息进行建模,公式如下:
| $ \begin{align} & C\left( B \right)=~\text{max}~f\left( x \right)\text{ }I\left( X;Y \right), \\ & \text{s}\text{.t}.~\ \ E\left[ {{Y}^{2}} \right]\ge B, \\ \end{align} $ | (9) |
其中,B表示接收端已收集的能量,C(B)表示与已收集的能量相关的容量。EHN中能量与信息联合传输问题已扩展到MIMO广播信道[51]、衰落信道[52]、MIMO干扰信道[53]等研究领域。系统中的能量传输主要基于SWIPT与WPCN技术,同时需要考虑当前接收端的实际限制,比如是否能够同时解码信息和收集能量[54]。下面主要讨论有关EHN中基于多天线SWIPT的波束成形设计与WPCN中的能量传输与管理策略的研究现状与技术综述。
5.2 能量收集网络中基于多天线SWIPT的波束成形设计基于无线信息与能量同步传输(SWIPT)研究面对的一个重要问题是随着传输距离的增加,能量传输的效率会越来越低,传播路径损耗也会越来越大。通过多天线技术可以实现空间复用,利用波束成形技术无须增加带宽或发射功率,即可提高射频(Radio frequency,RF)能量传输的效率,继而提高SWIPT的系统性能。本小节将回顾EHN中基于SWIPT的波束形成设计,包括无安全通信需求的SWIPT波束成形、有安全通信需求的SWIPT波束成形和能量波束形成设计。
5.2.1 无安全需求的SWIPT波束成形设计Zhang等[55]首先研究了三节点的MIMO网络中的波束成形,该网络包括一个发射器、一个能量收集器和一个信息接收器。假设发射器获知完美信道状态信息(Channel state information,CSI),通过权衡信息速率与RF能量传输来实现最佳的传输策略。Xiang等[56]将Zhang等[55]的研究成果扩展到发射器具有不完美CSI的情形下的三节点MISO网络,在保证目标速率的前提下,最大化最坏情况下的能量收集。此外,Xiang等[56]还考虑了波束成形的鲁棒性,将问题抽象成一个具有无限约束的非凸的二次规划问题,通过半定松弛将其转化为凸形式进行求解。结果表明,其最优波束成形矩阵解总是秩一的。
Zhang等[57]和Xu等[58]考虑具有多个信息接收器和能量收集器的多输入单输出(Multiple input and single output,MISO)下行广播系统。Zhang等[57]以最大化能量收集器中收集能量的最小值为目标,提出一个在信息接收器信干噪比(Signal-to-interference and noise ratio,SINR)约束和总发射功率约束下的鲁棒波束成形方案,通过半定松弛将问题转化为凸形式并通过标准的内点法求解。Xu等[58]以保证信息接收器各自的SINR需求的前提下最大化能量发送功率为目标,针对信息接收器是否具有干扰消除能力,将联合发射的波束形成权重和功率分配表述为非凸二次约束的二次规划问题,通过半定松弛得到了该问题的全局最优解。研究结果表明,两类信息接收器的解均为秩一的。与Zhang等[57]和Xu等[58]的研究不同,Khandaker等[59]考虑了具有多个功率分流接收器的MISO下行链路广播系统,联合设计了多播发射波束成形和接收器功率分流比,在每个接收器的信噪比(Signal to noise ratio,SNR)和能量收集约束下最小化基站的发射功率。
Li等[60-61]研究了用于双向中继系统的波束成形,其中两个单天线的源节点通过多个中继节点进行信息交换,并从这些中继节点的传输中收集RF能量。Li等研究了在发射功率受限和能量收集的约束下最大化加权总速率,设计了基于半定松弛和连续凸近似的迭代算法以得到局部最优解[60],并将该研究中理想的接收器架构拓展到了不完美CSI的放大转发中继系统中[61]。
Ng等[62]研究了SWIPT多点协作网络中的波束成形设计问题。该系统分别在信息接收器和能量收集器的最小SINR和最小能量收集约束下,联合优化网络总传输功率及回程链路的最大容量消耗。由于该问题为非凸规划形式,作者提出了一个次优的迭代算法,并证明其可以求得局部最优解。仿真结果表明,该方案的性能接近于基于穷举搜索的最优方案。该研究还展示出多点协作网络与集中式的多天线系统相比具有潜在的节能优势。
5.2.2 基于安全通信的SWIPT波束成形Liu等[63]和Ng等[64]研究了MISO下行链路系统中安全通信的波束成形方案,系统具有单一的目标信息接收器和信息与能量窃听节点。Liu等[63]研究了两种不同目标函数下的波束成形向量和功率分配设计。其一为在能量收集约束下最大化信息接收器的安全速率,其二是在信息接收器安全速率约束下,最大化能量收集器所收集的能量。两者均为非凸形式,通过半定松弛和一维搜索进行两步求解。Ng等[64]考虑了存在窃听节点的不完美CSI情形下,通过增加人工噪声实现安全通信。其CSI的不确定性引入非凸概率约束,通过数学运算与半定松弛求得最优解。能量收集效率随着接收器数量的增加而提高,但是其代价是需要增大发射功率。
尽管Liu等[63]和Ng等[64]设计了基于半定松弛的安全传输波束成形方案,但他们仅适用于单个信息接收器情形。Zhu等[65]和Ng等[66]研究了进行安全信息多播系统模型。Zhu等[65]提出采用秩二波束成形的Alamouti空时编码[67]来设计SWIPT的安全多播。推导得出秩二半定松弛紧致的充分条件,并提出了一个秩二的高斯随机过程以获得半定松弛不紧致情况下的次优解。Ng等[66]研究了基于时分多址(Time division multiple access,TDMA)的、由多个信息接收器组成的、存在被动窃听者的、分层传输系统中的信息安全多播问题,在空闲接收器的能量收集需求和多播接收器的异构服务质量(Quality of service,QoS)需求下,最小化总的发射功率。
Shi等[68]研究了MIMO广播系统中波束成形的设计。考虑一个发射器、信息接收器和能量窃听端组成的三节点网络,在发射功率约束和能量收集约束下,最大化安全信息速率的波束成形。作者提出等价的波束成形方案,使用不精确的块坐标下降算法来进行求解,并证明了该算法单调收敛于该问题的最优解。同时,作者还把算法扩展应用到了波束成形和人工噪声联合设计问题中。
5.3 无线供电通信网络与SWIPT相对应的另一项能量与信息联合传输的方案是无线供电通信网络(WPCN)。考虑图 5所示的WPCN系统,其中混合型接入点(Hybrid access point,H-AP)在下行链路(Down link, DL)阶段向多台无线设备广播能量,继而无线设备利用收集到的能量在上行链路(Up link, UL)阶段向H-AP通信。由于H-AP的半双工硬件约束,网络系统运行的一个周期往往包含两个阶段,即能量收集阶段和信息传输阶段。设备通过调整周期中两个阶段的时长比,继而实现能量收集与信息传输之间的均衡。总体而言,最优的时长比依赖于用户的无线信道状态[69]。WPCN的另一项难点在于设计高效的多址接入体系以协调UL阶段的用户信息传输。在传统的无线系统中,远离基站的用户通常所能实现的数据速率较低。这种现象在WPCN网络中更为突出,即远离H-AP的用户收集到的无线能量较少,但同时需要较多的能量用于UL阶段的信息传输,该问题成为双近远(Double near-far)问题。

|
| 图 5 WPCN模型和收集再传输协议 Fig. 5 WPCN model and the harvest-then-transmit protocol |
Liu等[70]指出,在UL阶段使用TDMA方式,H-AP能够为远距离用户分配更多的数据传输时间以解决双近远问题。另一方面,当H-AP具有多天线时,应用空分多址(Spatial division multiple access, SDMA)能够使得用户同时向H-AP传输数据,H-AP则使用多用户探测(Multi-user detection, MUD)技术解码用户数据。SDMA通常情况下能够实现比TDMA更高的频谱效率。此外,通过UL阶段的用户传输功率控制和DL阶段的能量波束成形设计能够缓解双近远问题,H-AP使用能量波束成形向远距离用户发送更多的能量,同时允许他们比较近用户发送更大的功率等级从而均衡系统吞吐量。另一项缓解双近远问题的方法是使用用户协作。
WPCN的高效运行依赖于H-AP端精确的信道状态信息,信息解码与资源分配均需要获取精确的CSI。与传统无线网络相似,WPCN的吞吐量性能得益于较长的信道估计周期,但又受限于较短的能量/信息传输时间。因此,Zeng等[71]提出WPCN的具体设计需要均衡各能量之间的约束,如H-AP用于解码控制信号的信道估计、CSI反馈传输、用于计算UL/DL相互作用的信道估计等。然而,用于信道估计的能量越多就会导致传输速率的下降,更精确的CSI估计和更有效的波束成形则能提高系统性能。因此,该问题是最优化问题。
另一项提高WPCN性能的技术是大规模MIMO,即在H-AP部署大量的天线从而获得较高的天线阵列增益。一方面,大量天线所提供的较大等级的自由度使得在UL信息传输阶段能够通过空间复用从而服务更多的用户。另一方面,大量天线阵列提升了DL节点能量波束成形的性能。Yang等[72]指出在WPCN中应用多天线MIMO,能够使得吞吐量提升数倍且增大网络的覆盖范围。同时表明,H-AP端的多天线并不会导致传输系统的高处理复杂度和功耗,多用户到H-AP信道的渐近正交特性简化了波束成形设计、多址接入控制和功率控制方案。
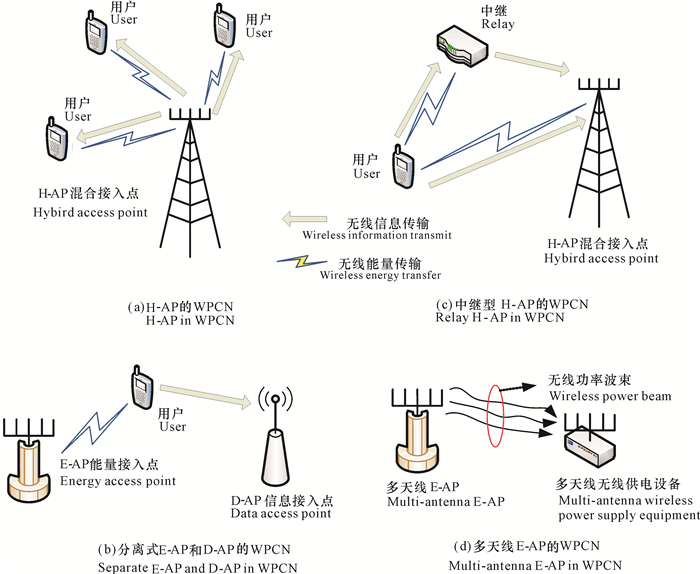
在WPCN中,无线设备仅使用从无线充电站处收集的能量完成通信。通常考虑两种无线充电装置。第一种为专用的无线充电站,作为能量接入点(Energy access point, E-AP)。第二种为混合接入点H-AP,能够在无线充电的基础上支持数据通信。目前研究相关的4种系统类型如图 6所示,其中,图 6a表示基于H-AP的WPCN模型,部署H-AP实现下行无线充电和上行信息传输;图 6b表示基于专用E-AP的WPCN模型,分别使用E-AP和数据接入点(Data access point, D-AP)实现下行无线充电和上行信息传输;图 6c表示H-AP中继型WPCN模型,系统使用中继实现设备到H-AP的上行信息传输;图 6d表示多天线E-AP的WPCN模型,由E-AP配备多天线,通过将能量波束朝向指定方向从而提升充电效率。
|
| 图 6 WPCN中无线能量传输的相关模型 Fig. 6 Related models of WPT in WPCN |
5.3.1 基于H-AP的WPCN
在H-AP的WPCN中,主要任务是分配资源以最大化无线设备的可实现吞吐量。Ju等[69]提出收集再传输协议,即首先配置网络设备在DL阶段从H-AP收集能量,然后在UL阶段基于TDMA,利用收集的能量向H-AP独立地发送信息。作者优化了半双工H-AP的无线充电与信息传输的时间分配系数,同时为了解决双近远问题,引入性能矩阵(即通用吞吐量)增加约束,使得所有网络设备不论其位置均应实现相同的吞吐量。接着提出基于简单二分法搜索的迭代算法,求解通用吞吐量最大化问题。研究结果表明,该迭代算法能够有效求解双近远问题,但其折损了部分总吞吐量作为代价。Ju等[73]还拓展了上述研究,使用全双工的H-AP,联合优化下行阶段中H-AP的功率分配与时间分配和上行阶段中用户的时间分配。
Ju等[69, 73]、Liu等[70]、Zeng等[71]和Yang等[72]考虑的用户设备均已知其确定位置。Zhao等[74]则使用随机几何方法分析了设备位置随机的情形,以最大化系统空间吞吐量为目标,提出联合框架优化上行传输功率以及下行能量传输和上行信息传输的时间分配比,同时在配备电池和无电池情形下实现对空间吞吐量优化问题的求解。数值计算结果验证了电池容量对系统空间吞吐量的影响。
不同于上述研究,Liu等[70]研究了多天线H-AP的WPCN系统。多天线H-AP需要通过调整能量波束成形权重控制不同设备的能量传输速率,为此,作者以最大化设备的最小吞吐量为优化目标,建立了非凸问题以分别最优化时间分配、下行能量波束成形、上行传输功率分配和波束成形接收,以此解决双近远问题。
5.3.2 专用E-AP的能量传输策略对于专用E-AP的WPCN,主要目标为控制E-AP的无线充电功率以实现最优化目标。Zhao等[74]基于收集再传输协议,提出基于能量、时间和信息误差率约束下均衡能量收集和信息传输分时的最优化策略。Zhou等[75]研究了全双工系统,将能量收集和数据传输在两个分开的时变信道中进行,并在基于所有信道信息均为先验已知且用户电池容量无限大的假设下,提出实现最优功率分配的有效算法。然而,该研究仅考虑了单一设备,无法适用多设备的功率分配场景。
Sun等[76]拓展了Zhou等[75]的研究,考虑了多设备和多天线的情形。基于TDMA,系统总吞吐量最大化问题为非凸的,需联合优化时间分配和能量波束成形。对此,Sun等[76]使用半定松弛技术将问题变为凸形式,并证明了半定松弛逼近的全局优化的密闭性。Bicen等[77]则假设E-AP和设备机会性接入相同信道以进行无线能量和信息传输,提出E-AP的功率控制策略以最小化E-AP期望失真度下的能量消耗。仿真实验结果验证了估计误差、E-AP数量和其功率等级之间的均衡关系。
5.3.3 中继H-AP的能量传输策略基于中继的WPCN的主要问题是设计合理的运行协议从而协调数据传输和无线充电以最大化系统性能。Chen等[78]设计了一种收集再协作协议,规划了用户设备和中继先收集能量,然后在上行区间内进行协作信息传输。基于该协议,对于单一中继的延迟受限传输,提出瑞利衰落信道的平均系统吞吐量的闭式逼近表达式;对于多中继节点的情形,提出了两种不同的系统吞吐量逼近形式。Che等[79]进一步提出了能量协作协议和双向协作协议,前者允许一个中继和H-AP在下行能量传输阶段实现协作;后者则令中继先和H-AP协作完成下行能量传输,继而帮助用户设备完成上行信息传输。
5.3.4 多天线E-AP的能量传输策略多天线E-AP的主要任务是设计波束成形策略和/或CSI反馈机制以提升无线充电效率,并不考虑信息传输的相关任务。Yang等[80]设计了不完美CSI反馈下点对点MISO系统的自适应能量波束成形。该系统运行基于帧的协议,首先规划接收端通过发送端发送的导频信号和其反馈的CSI估计信道状态,然后发送端通过波束成形发送RF能量。为了最大化收集到的能量,作者研究了信道估计区间和功率传输区间以及能量传输之间的均衡关系,针对导频长度可变和固定的情形分别提出了最优在线导频长度和离线导频长度。最终传输功率的分配则依据信道估计功率和最优导频长度制定。
基于信道互易性,E-AP能够利用来自用户设备的专用反向链路训练信号估计信道状态。Zeng等考虑了点到点MIMO能量波束成形系统,实现了能量波束成形系统中训练区间和无线功率传输之间的均衡[71],并拓展了这一研究,考虑了更为复杂的宽带频率选择性衰落信道,为能量传输效率提供附加的频率分集增益[81]。为了同时实现分集和波束成形增益,作者还引入双相位信道训练系统,其中在第一相位中,E-AP通过用户设备发送的导频信号选择具有最大天线和功率增益的子带集合;在其后第二相位中,E-AP利用子带集合中附加的导频信道估计MISO信道。数值计算结果与分析验证了所述过程能够基于能量约束训练最优均衡实现频率分集和能量波束成形增益。
6 展望EHN融合新能源的优点,作为传统网络供能的补充和替换,大大增加了网络生命周期和覆盖范围。同时,EHN中能量与信息联合传输的发展,使得在现有网络无须替换的基础上,提高了资源的复用率以及节点和设备之间的协作等级,为网络提供了更智能的自治能力、更广泛的覆盖范围、更高度集成的系统能力等美好前景。本文在分析EHN研究历程及现状的基础上,重点从信息论视角、能量收集模型、离线与在线能量规划、无线能量与信息联合传输等4个方面综述近年EHN网络的研究现状与相关结论。我们也利用场景生成技术、不确定规划、凸优化等方法,分别研究了EHN中能量收集模拟技术、节点运行可靠性评估以及网络效益最大化等问题,得出相应结论并利用仿真计算验证结论的正确性和所述方法的有效性,为EHN的发展部署提供理论依据[20, 43]。针对EHN未来发展,我们认为可以开展以下研究:
(1) EHN中能源网与信息网的融合与协作。EHN的发展已不再受限于传统的低能耗型的传感网络,同时向着更高能耗和更好能量收集等级的应用发展,如新能源基站、智能电网、高空无人机网络、深海和星际探测等,这类应用场景下,EHN需要很好地融合系统任务或网络节点间的能量协作和信息交互,实现多场景下混合接入的自组智能控制运行,协调系统诸多因素。该研究前景深远,同时也具有较大的复杂度和不确定性。
(2) EHN与物联网的融合。EHN具有自给自足的优势,与物联网的结合能够实现真正意义上的万物互联。传统物联网的标准与协议在EHN中失效,研究如何定义及实现EHN的物联协议,实现诸如从人体嵌入式机器人到可穿戴设备,从监控节点到通信基站和数据中心等复杂应用下的数据协调与任务处理,以及节点本地或服务器端针对任务数据及能量数据的甄别和决策,均为未来亟待解决的有意义的问题。该项研究结合了大数据、机器视觉、人工智能等新兴技术,为EHN的研究提供深远前景。
(3) EHN的安全性问题。EHN如传统网络一样,需要考虑信息的安全性,同时也应考虑能量收集与传输的安全性问题,网络中可能含有恶意的信息窃听节点,也可能含有恶意的能量接收节点。因此,结合波束成形、人工噪声及加密等技术,实现能量的安全传输成为亟待解决的问题,同时通信过程中也包含有能量状态信息,应确保该部分信息的安全以使得节点或设备间能够正确共享能量,实现节点间能量的协作与传输。
网络的应用朝着多样化和智能化的方向发展,EHN在未来逐渐融入和替换部分传统网络,出现了多种网络类型的混合、多种能源与信息交互方式的混合,因此从科学研究的角度而言,需要更加系统化智能化的解决方案以适应各种场景及应用的需求。该领域也将得到更多学者的关注与研究。
| [1] |
ULUKUS S, YENER A, ERKIP E, et al. Energy harvesting wireless communications:A review of recent advances[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 360-381. DOI:10.1109/JSAC.2015.2391531 |
| [2] |
LU X, WANG P, NIYATO D, et al. Wireless charging technologies:Fundamentals, standards, and network applications[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1413-1452. |
| [3] |
曹自平, 王楚, 袁明, 等. 环境能量采集技术的研究现状及发展趋势[J]. 南京邮电大学学报:自然科学版, 2016, 36(4): 1-10. |
| [4] |
RAVI A K, SHASHANK P. A review on low-grade thermal energy harvesting:Materials, methods and devices[J]. Materials, 2018, 11(8): 1433. DOI:10.3390/ma11081433 |
| [5] |
OZEL O, ULUKUS S. Achieving AWGN capacity under stochastic energy harvesting[J]. IEEE Transactions on Information Theory, 2012, 58(10): 6471-6483. DOI:10.1109/TIT.2012.2204389 |
| [6] |
OZEL O, ULUKUS S.AWGN channel under time-varying amplitude constraints with causal information at the transmitter[C]//Conference Record of the 45th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA: IEEE, 2011: 373-377.
|
| [7] |
TUTUNCUOGLU K, OZEL O, YENER A, et al. Binary energy harvesting channel with finite energy storage[C]//2013 IEEE International Symposium on Information Theory. Istanbul, Turkey: IEEE, 2013: 1591-1595.
|
| [8] |
SMITH J G, SMITH J G. The information capacity of amplitude and variance constrained scalar gaussian channels[J]. Information and Control, 1971, 18(3): 203-219. DOI:10.1016/S0019-9958(71)90346-9 |
| [9] |
SHANNIN C E. Channels with side information at the transmitter[J]. IBM Journal of Research and Development, 1958, 2(4): 289-293. DOI:10.1147/rd.24.0289 |
| [10] |
OZEL O, ULUKUS S. On the capacity region of the Gaussian MAC with batteryless energy harvesting transmitters[C]//2012 IEEE Global Communications Conference. Anaheim, CA, USA: IEEE, 2012: 2385-2390.
|
| [11] |
ANANTHARAM V, VERDU S. Bits through queues[J]. IEEE Transactions on Information Theory, 1996, 42(1): 4-18. DOI:10.1109/18.481773 |
| [12] |
KONG H B, FLINT I, WANG P, et al. Exact performance analysis of ambient RF energy harvesting wireless sensor networks with ginibre point process[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3769-3784. DOI:10.1109/JSAC.2016.2621360 |
| [13] |
KIM J W, BARRADO J R R, JEON D K. Time and energy efficient relay transmission for Multi-Hop wireless sensor networks[J]. Sensors:Basel, 2016, 16(7): 985. DOI:10.3390/s16070985 |
| [14] |
LIU J, DAI H, CHEN W. Delay optimal scheduling for energy harvesting based communications[J]. IEEE Journal on Selected Areas in Communications, 2013, 33(3): 452-466. |
| [15] |
HO C K, KHOA P D, MING P C. Markovian models for harvested energy in wireless communications[C]//12th IEEE International Conference on Communication Systems.Singapore: IEEE, 2010: 311-315.
|
| [16] |
ZOU T, LIN S, FENG Q, et al. Energy-efficient control with harvesting predictions for solar-powered wireless sensor networks[J]. Sensors:Basel, 2016, 16(1): 53. DOI:10.3390/s16010053 |
| [17] |
VALERA A C, SOH W S, TAN H P. Enabling sustainable bulk transfer in environmentally-powered wireless sensor networks[J]. Ad Hoc Networks, 2017, 54: 85-98. DOI:10.1016/j.adhoc.2016.10.008 |
| [18] |
PART P, MARCO P D, JOHANSSON K H. Cross-layer optimization for industrial control applications using wireless sensor and actuator mesh networks[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 3250-3259. DOI:10.1109/TIE.2016.2631530 |
| [19] |
MISRA S, MAJD N E, HUANG H. Approximation algorithms for constrained relay node placement in energy harvesting wireless sensor networks[J]. IEEE Transactions on Computers, 2014, 63(12): 2933-2947. DOI:10.1109/TC.2013.171 |
| [20] |
王哲, 李陶深, 叶进, 等. 基于场景生成的能量收集网络模拟方法[J]. 电子学报, 2018, 46(8): 1931-1937. DOI:10.3969/j.issn.0372-2112.2018.08.018 |
| [21] |
YANG J, ULUKUS S. Optimal packet scheduling in an energy harvesting communication system[J]. IEEE Transactions on Communications, 2012, 60(1): 220-230. DOI:10.1109/TCOMM.2011.112811.100349 |
| [22] |
TUTUNCUOGLU K, YENER A. Optimum transmission policies for battery limited energy harvesting nodes[J]. IEEE Transactions on Wireless Communications, 2010, 11(3): 1180-1189. |
| [23] |
OZEL O, TUTUNCUOGLU K, YANG J, et al. Trans-mission with energy harvesting nodes in fading wireless channels:Optimal policies[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(8): 1732-1743. DOI:10.1109/JSAC.2011.110921 |
| [24] |
HO C K, ZHANG R. Optimal energy allocation for wireless communications with energy harvesting constraints[J]. IEEE Transactions on Signal Processing, 2011, 60(9): 4808-4818. |
| [25] |
YANG J, OZEL O, ULUKUS S. Broadcasting with an energy harvesting rechargeable transmitter[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 571-583. DOI:10.1109/TWC.2011.120911.101813 |
| [26] |
OZEL O, YANG J, ULUKUS S. Optimal broadcast scheduling for an energy harvesting rechargeable transmitter with a finite capacity battery[J]. IEEE Transactions on Wireless Communications, 2012, 11(6): 2193-2203. DOI:10.1109/TWC.2012.032812.110813 |
| [27] |
ANTEPLI M A, UYSAL-BIYIKOGLU E, ERKAL H. Optimal packet scheduling on an energy harvesting broadcast link[J]. IEEE Journal on Selected Areas in Communications, 2010, 29(8): 1721-1731. |
| [28] |
OZEL O, YANG J, ULUKUS S. Optimal transmissi-on schemes for parallel and fading Gaussian broadcast channels with an energy harvesting rechargeable transmitter[J]. Computer Communications, 2013, 36(12): 1360-1372. DOI:10.1016/j.comcom.2012.04.010 |
| [29] |
YANG J, ULUKUS S. Optimal packet scheduling in a multiple access channel with energy harvesting transmitters[J]. Journal of Communications and Networks, 2012, 14(2): 140-150. DOI:10.1109/JCN.2012.6253062 |
| [30] |
KAYA O, ULUKUS S. Achieving the capacity region boundary of fading CDMA channels via generalized iterative waterfilling[J]. IEEE Transactions on Wireless Communications, 2004, 5(11): 3215-3223. |
| [31] |
YU W, RHEE W, BOYD S P, et al. Iterative water-filling for Gaussian vector multiple-access channels[J]. IEEE Transactions on Information Theory, 2004, 50(1): 145-152. DOI:10.1109/TIT.2003.821988 |
| [32] |
TUTUNCUOGLU K, YENER A. Optimal power policy for energy harvesting transmitters with inefficient energy storage[C]//201246th Annual Conference on Information Sciences and Systems. Princeton, NJ, USA: IEEE, 2012: 1.
|
| [33] |
GUNDUZ D, DEVILLERS B. Two-hop communication with energy harvesting[C]//20114th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing. San Juan, Puerto Rico: IEEE, 2011: 201-204.
|
| [34] |
HUANG C, ZHANG R, CUI S. Throughput maximization for the Gaussian relay channel with energy harvesting constraints[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(8): 1469-1479. DOI:10.1109/JSAC.2013.130811 |
| [35] |
ORHAN O, ERKIP E.Optimal transmission policies for energy harvesting two-hop networks[C]//201246th Annual Conference on Information Sciences and Systems. Princeton, NJ, USA: IEEE, 2012: 1.
|
| [36] |
TUTUNCUOGLU K, VARAN B, YENER A. Energy harvesting two-way half-duplex relay channel with decode and forward relaying: Optimum power policies[C]//201318th International Conference on Digital Signal Processing. IEEE, Santorini, Greece, 2014: 1.
|
| [37] |
VARAN B, YENER A. The energy harvesting two-way decode-and-forward relay channel with stochastic data arrivals[C]//2013 IEEE Global Conference on Signal and Information Processing. Austin, TX, USA: IEEE, 2013: 371-374.
|
| [38] |
ORHAN O, GUNDUZ D, ERKIP E.Throughput max-imization for an energy harvesting communication system with processing cost[C]//2012 IEEE Information Theory Workshop. Lausanne, Switzerland: IEEE, 2012: 84-88.
|
| [39] |
XU J, ZHANG R. Throughput optimal policies for energy harvesting wireless transmitters with non-ideal circuit power[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(2): 322-332. DOI:10.1109/JSAC.2014.141212 |
| [40] |
ORHAN O, GUNDUZ D, ERKIP E. Energy harvest-ing broadband communication systems with processing energy cost[J]. IEEE Transactions on Wireless Communications, 2014, 13(11): 6095-6107. DOI:10.1109/TWC.2014.2328600 |
| [41] |
MICHELUSI N, STAMATIOU K, ZORZI M. On optimal transmission policies for energy harvesting devices[C]//2012 Information Theory and Applications Workshop. San Diego, CA, USA: IEEE, 2012: 249-254.
|
| [42] |
BERTSEKAS D P. Dynamic programming and optimal control[M]. Cambridge: Athena Scientific, 2000.
|
| [43] |
王哲, 李陶深, 叶进, 等. 基于不确定理论的能量收集可靠性建模及规划[J]. 通信学报, 2018, 39(5): 166-176. |
| [44] |
CHIASSON J, VAIRAMOHAN B. Estimating the state of charge of a battery[J]. IEEE Transactions on Control Systems Technology, 2005, 13(3): 465-470. DOI:10.1109/TCST.2004.839571 |
| [45] |
MICHELUSI N, STAMATIOU K, BADIA L, et al.Operation policies for energy harvesting devices with imperfect state-of-charge knowledge[C]//2012 IEEE International Conference on Communications. Ottawa, ON, Canada: IEEE, 2012: 5782-5787.
|
| [46] |
MICHELUSI N, BADIA L, CARLI R, et al. Correlated energy generation and imperfect state-of-charge knowledge in energy harvesting devices[C]//8th International Wireless Communications and Mobile Computing Conference. Limassol, Cyprus: IEEE, 2012: 401-406.
|
| [47] |
MICHELUSI N, BADIA L, CARLI R, et al. Energy management policies for harvesting-based wireless sensor devices with battery degradation[J]. IEEE Transactions on Communications, 2013, 61(12): 4934-4947. DOI:10.1109/TCOMM.2013.111113.130022 |
| [48] |
NISHIMOTO H, KAWAHARA Y, ASAMI T. Prototype implementation of ambient RF energy harvesting wireless sensor networks[C]//IEEE Sensors 2010 Conference. Kona, HI, USA: IEEE, 2012: 1282-1287.
|
| [49] |
NINTANAVONGSA P, NADERI M Y, CHOWDHURY K R. A dual-band wireless energy transfer protocol for heterogeneous sensor networks powered by RF energy harvesting[C]//2013 International Computer Science and Engineering Conference. Nakorn Pathom, Thailand: IEEE, 2013: 387-392.
|
| [50] |
WANG X, MORTAZAWI A.High sensitivity RF energy harvesting from AM broadcasting stations for civilian infrastructure degradation monitoring[C]//2013 IEEE International Wireless Symposium. Beijing: IEEE, 2013: 1-8.
|
| [51] |
PARKS A N, SAMPLE A P, ZHAO Y, et al. A wireless sensing platform utilizing ambient RF energy[C]//2013 IEEE Radio and Wireless Symposium. Austin, TX, USA: IEEE, 2013: 331-333.
|
| [52] |
TAKACS A, AUBERT H, DESPOISSE L, et al. Microwave energy harvesting for satellite applications[J]. Electronics Letters, 2013, 49(11): 722-723. DOI:10.1049/el.2013.0372 |
| [53] |
TAKACS A, AUBERT H, FREDON S, et al. K-band energy harvesting circuits for satellite application[C]//2013 European Microwave Conference. Nuremberg, Germany: IEEE, 2013: 991-994.
|
| [54] |
TAKACS A, AUBERT H, DESPOISSE L, et al. Design and implementation of a rectenna for satellite application[C]//2013 IEEE Wireless Power Transfer. Perugia, Italy: IEEE, 2013: 183-186.
|
| [55] |
ZHANG R, HO C K. MIMO broadcasting for simultaneous wireless information and power transfer[J]. IEEE Transactions on Wireless Communication, 2013, 12(5): 1989-2001. DOI:10.1109/TWC.2013.031813.120224 |
| [56] |
XIANG Z, TAO M. Robust beamforming for wireless information and power transmission[J]. IEEE Wireless Communication Letters, 2012, 1(4): 372-375. DOI:10.1109/WCL.2012.053112.120212 |
| [57] |
ZHANG H, SONG K, HUANG Y, et al. Energy harvesting balancing technique for robust beamforming in multiuser MISO SWIPT system[C]//2013 International Conference on Wireless Communications and Signal Processing. Hangzhou: IEEE, 2013: 1-5.
|
| [58] |
XU J, LIU L, ZHANG R. Multiuser MISO beamforming for simultaneous wireless information and power transfer[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4798-4810. DOI:10.1109/TSP.2014.2340817 |
| [59] |
KHANDAKER M R A, WONG K K. SWIPT in MISO multicasting systems[J]. IEEE Wireless Communication Letters, 2014, 3(3): 277-280. DOI:10.1109/WCL.2014.030514.140057 |
| [60] |
LI D, SHEN C, QIU Z. Two-way relay beamforming for sum-rate maximization and energy harvesting[C]//2013 IEEE International Conference on Communications. Budapest, Hungary: IEEE, 2013: 3115-3120.
|
| [61] |
LI D, SHEN C, QIU Z. Sum rate maximization and energy harvesting for two-way AF relay systems with imperfect CSI[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver, BC, Canada IEEE, 2013: 4958-4962.
|
| [62] |
NG D W K, SCHOBER R. Resource allocation for coordinated multipoint networks with wireless information and power transfer[C]//2014 IEEE Global Communications Conference. Austin, TX, USA: IEEE, 2014: 1-7.
|
| [63] |
LIU L, ZHANG R, CHUA K C. Secrecy wireless information and power transfer with MISO beamforming[J]. IEEE Transactions on Signal Processing, 2014, 62(7): 1850-1863. DOI:10.1109/TSP.2014.2303422 |
| [64] |
NG D W K, LO E S, SCHOBER R. Robust beamforming for secure communication in systems with wireless information and power transfer[J]. IEEE Transactions on Wireless Communication, 2014, 13(8): 4599-4615. DOI:10.1109/TWC.2014.2314654 |
| [65] |
ZHU B, GE J, HUANG Y, et al. Rank-two beam-formed secure multicasting for wireless information and power transfer[J]. IEEE Signal Processing Letters, 2014, 21(2): 199-203. |
| [66] |
NG D W K, SCHOBER R, ALNUWEIRI H. Secure layered transmission in multicast systems with wireless information and power transfer[C]//2014 IEEE International Conference on Communications. Sydney, NSW, Australia: IEEE, 2014: 1-7.
|
| [67] |
WU S X, SO A M C, MA W K. Rank-two transmit beamformed Alamouti space-time coding for physical-layer multicasting[C]//2012 IEEE International Conference on Acoustics, Speech and Signal Processing. Kyoto, Japan: IEEE, 2012: 2793-2796.
|
| [68] |
SHI Q, XU W, WU J, et al. Secure beamforming for MIMO broadcasting with wireless information and power transfer[J]. IEEE Transactions on Wireless Communications, 2015, 14(5): 2841-2853. DOI:10.1109/TWC.2015.2395414 |
| [69] |
JU H, ZHANG R. Throughput maximization in wireless powered communication networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 418-428. DOI:10.1109/TWC.2013.112513.130760 |
| [70] |
LIU L, ZHANG R, CHUA K C. Multi-antenna wireless powered communication with energy beamforming[J]. IEEE Transactions on Communications, 2014, 62(12): 4349-4361. DOI:10.1109/TCOMM.2014.2370035 |
| [71] |
ZENG Y, ZHANG R. Optimized training design for wireless energy transfer[J]. IEEE Transactions on Communications, 2015, 63(2): 536-550. DOI:10.1109/TCOMM.2014.2385077 |
| [72] |
YANG G, HO C K, ZHANG R, et al. Throughput optimization for massive MIMO systems powered by wireless energy transfer[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(8): 1-1. DOI:10.1109/JSAC.2015.2445671 |
| [73] |
JU H, ZHANG R. Optimal resource allocation in full-duplex wireless-powered communication network[J]. IEEE Transactions on Communications, 2014, 62(10): 3528-3540. DOI:10.1109/TCOMM.2014.2359878 |
| [74] |
ZHAO F, WEI L, CHEN H. Optimal time allocation for wireless information and power transfer in wireless powered communication systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1830-1835. DOI:10.1109/TVT.2015.2416272 |
| [75] |
ZHOU X, HO C K, ZHANG R. Wireless power meets energy harvesting:A joint energy allocation approach[J]. IEEE Transactions on Wireless Communications, 2016, 15(5): 3481-3491. DOI:10.1109/TWC.2016.2522410 |
| [76] |
SUN Q, ZHU G, SHEN C, et al. Joint beamforming design and time allocation for wireless powered communication networks[J]. IEEE Communications Letters, 2014, 18(10): 1783-1786. DOI:10.1109/LCOMM.2014.2347958 |
| [77] |
BICEN A O, AKAN O B. Energy-efficient RF source power control for opportunistic distributed sensing in wireless passive sensor networks[C]//2012 IEEE Symposium on Computers and Communications. Cappadocia, Turkey: IEEE, 2012: 738-743.
|
| [78] |
CHEN H, LI Y, REBELATTO J L, et al. Harvest-then-cooperate:Wireless-powered cooperative communications[J]. IEEE Transactions on Signal Processing, 2015, 63(7): 1700-1711. DOI:10.1109/TSP.2015.2396009 |
| [79] |
CHE Y L, DUAN L, ZHANG R. Spatial throughput maximization of wireless powered communication networks[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(8): 1. DOI:10.1109/JSAC.2015.2445671 |
| [80] |
YANG G, HO C K, GUAN Y L. Dynamic resource allocation for multiple-antenna wireless power transfer[J]. IEEE Transactions on Signal Processing, 2014, 62(14): 3565-3577. DOI:10.1109/TSP.2014.2328980 |
| [81] |
ZENG Y, ZHANG R. Optimized training for net energy maximization in multi-antenna wireless energy transfer over frequency-selective channel[J]. IEEE Transactions on Communications, 2015, 63(6): 2360-2373. DOI:10.1109/TCOMM.2015.2424420 |



