2. 北京控制与电子技术研究所, 北京 102308
2. Beijing Institute of Control and Electronic Technology, Beijing, 102308, China
微波源是产生微波的核心部件[1]。为满足微波能应用对功率和频率的要求,绝大多数的微波源是真空电子管,包括磁控管、行波管和速调管等,其中磁控管不仅可以放大信号还能够产生振荡[2]。磁控管的阳极与阴极间电势差较大,有利于产生较强的静电场。磁控管中的外置磁铁或线包被用来产生与电场正交的磁场,施加的磁场对加速运行的电子产生切向作用力。在电场与磁场的共同作用下,电子在磁控管中沿螺旋方向运动,产生旋转的电子云。当电子经过谐振腔时,电子云在谐振腔中引起谐振,谐振频率由腔的尺寸大小决定。电磁能量从其中一个谐振腔通过同轴线或波导耦合到微波传输线。磁控管的输出功率可调,如果是脉冲磁控管,可以通过调节工作周期、阴极电流、磁场强度和开关占空比等改变输出功率;如果是连续波磁控管,可以通过改变阴极电流幅度或磁场强度来改变输出功率[3]。
磁控管在20世纪20年代兴起,历经几十年的发展在功率、频率等各方面性能上面有很大突破[4]。目前磁控管在频率稳定性、工作寿命等方面仍存在诸多问题,为此普遍采用隔模带的方式来增大模式分隔度,从而提高磁控管的稳定性[5-6]。此外,制约磁控管寿命的另一问题是散热[7],这是因为在磁控管各部件体积缩小的过程中,功率增加,热流密度急剧上升,磁控管处于过应力(电、热或机械应力)的状态,导致大多数磁控管过早失效。虽然磁控管结构复杂并大量使用诸如金属-金属、金属-陶瓷接头等真空密封工艺,但对于大功率连续波磁控管,最容易出现热失效的部件是阴极和阳极叶片[8]。处于工作状态下的磁控管阳极受到阴极发射电子的热轰击、阳极工作面上高频电流流动产生的涡流热以及阴极的热辐射,对比前两种热,阴极的热辐射可以忽略[9]。如果磁控管没有性能完善的冷却设计,磁控管可能出现频率热漂移大、打火次数增加等现象,严重时可能出现腔体变形、放气、叶片局部熔化等问题,使磁控管过早损坏[10]。
本文从提高磁控管工作稳定性和延长寿命的角度出发,首先,利用等效电路方法推导谐振腔系统的频率,利用仿真软件对磁控管在无隔模带、单隔模带和双隔模带下的工作模式、谐振频率和品质因数进行对比;其次,对扇形和扇槽形阳极叶片的温度、热流进行理论推导和仿真模拟,通过对比不同冷却条件下谐振系统热应力、形变、温度和谐振频率,设计出满足大功率连续波磁控管散热的冷却水路和相匹配的冷却条件。最后,通过温度与模式谐振频率间的对应关系得到腔体的热漂移曲线,对工程实践具有指导意义。
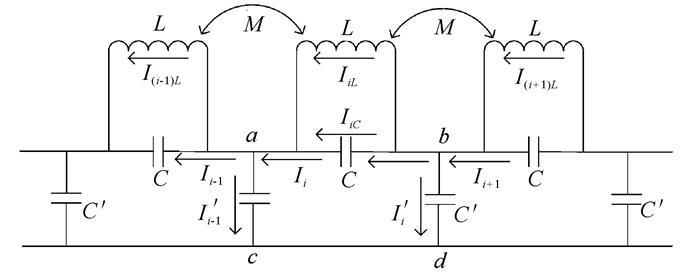
1 磁控管高频场与热应力场的数学推导 1.1 高频电磁场分析采用等效电路的方法对无隔模带磁控管谐振频率进行理论推导。第i-1、i和i+1段无隔模带磁控管谐振系统的等效电路模型如图 1所示,其中C和L分别为单个谐振腔的等效电容和等效电感,C′和M分别是相邻两个谐振腔之间的耦合电容和互感。该模型充分考虑谐振系统的电耦合与磁耦合:阳极和位于谐振腔中心的阴极间具有电容,导致腔体间具有电容耦合[11];由于各个谐振腔之间并不是封闭的,任意几个谐振腔间有磁场的穿插交换,这导致谐振系统磁耦合的存在。阳极叶片越长,磁耦合越弱,此时谐振系统以容性的电耦合为主;对于较短的阳极块,则以磁耦合为主[12-13]。
|
| 图 1 无隔模带磁控管谐振系统等效电路 Fig. 1 Equivalent circuit of the unstrapped magnetron's resonant system |
当第i个小谐振腔发生谐振时,ab间的等效导纳和输入导纳之和为0。第i个谐振腔的等效导纳Y1和从ab两点看向互作用空间的输入导纳Y2分别为
| $ \begin{array}{l} \;\;\;\;\;\;{Y_1} = j\omega C - j\frac{1}{{\omega {\rm{ }}\left( {L - 2M{\rm{cos}}\varphi } \right)}} = \\ j\omega C\left[ {1 - \frac{{\omega _0^2}}{{{\omega ^2}\left( {1 - \frac{M}{L}{\rm{cos}}\varphi } \right)}}} \right], \end{array} $ | (1) |
| $ {Y_2} = {\rm{ }}\frac{{j\omega C\prime }}{{2\left( {1 - {\rm{cos}}\varphi } \right)}}。$ | (2) |
由谐振条件Bi=Im(Yi)=Im)Y1+Y2)=0,可以得到
| $ \omega C\left[ {1 - \frac{{\omega _0^2}}{{{\omega ^2}\left( {1 - \frac{M}{L}{\rm{cos}}\varphi } \right)}}} \right] + \frac{{\omega C\prime }}{{2\left( {1 - {\rm{cos}}\varphi } \right)}} = 0, $ | (3) |
因此,无隔模带磁控管谐振角频率ω(用ωn来代替)为
| $ {\omega _n} = \frac{{{\omega _0}}}{{\sqrt {\left[ {1 + \frac{{C\prime }}{{2C\left( {1 - {\rm{cos}}\varphi } \right)}}} \right]} \left( {1 - \frac{{2M{\rm{cos}}\varphi }}{L}} \right)}}{\rm{, }} $ | (4) |
其中,ω0是单个谐振腔的谐振角频率,
| $ \begin{array}{l} \;\;\;\;\;\;\gamma = \left| {\frac{{\Delta \omega }}{{{\omega _\pi }}}} \right| = \left| {1 - \frac{{{\omega _{\frac{N}{2} - 1}}}}{{{\omega _\pi }}}} \right| = |1 - \\ \sqrt {\frac{{\left[ {1 + C\prime /\left( {4C} \right)} \right]\left( {1 + 2M/L} \right)}}{{\left\{ {1 + \frac{{C\prime }}{{2C\left[ {1 + {\rm{cos}}\left( {2\pi /N} \right)} \right]}}} \right\}\left[ {1 + \frac{{2M{\rm{cos}}\left( {2\pi /N} \right)}}{L}} \right]}}} {\rm{ }}|。\end{array} $ | (5) |
通过上述分析发现,在确定腔体个数的前提下,无隔模带磁控管的谐振频率ωn由单个腔体的谐振频率ω0、电耦合C′/C与磁耦合M/L共同决定。电耦合与磁耦合的相对大小也对模式分隔度产生影响,谐振频率与模式分隔度的变化趋近于两种耦合中占主要作用的一方[14-15]。
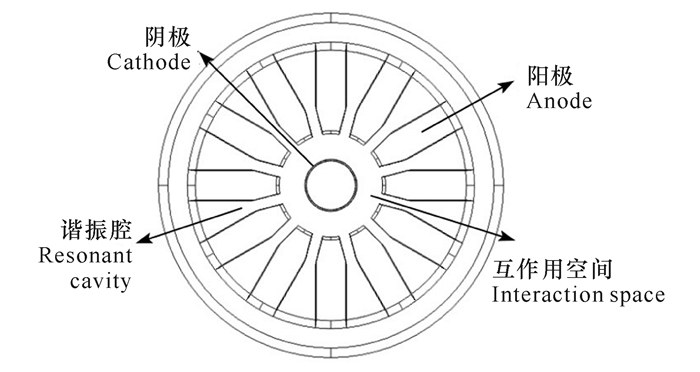
以12腔扇槽形谐振系统为例,该系统由4个部分组成:圆柱形阴极、扇槽形阳极叶片、谐振腔、互作用空间等(图 2)。利用COMSOL软件中的频域电磁波(Electromagnetic waves, frequency domain)模块构建物理场并使用本征模(Eigenfrequency)求解器对该谐振系统的工作模式和品质因数进行数值仿真。由于高频电磁波对阳极叶片具有一定的穿透深度,但穿透深度很小,因此设置谐振腔的径向边界条件即阳极叶片设置为阻抗边界,在谐振腔轴向上设置散射边界条件。
|
| 图 2 12腔扇槽形谐振系统的截面示意图 Fig. 2 Schematic diagram of a fan-slop-shaped resonant system with 12 cavities |
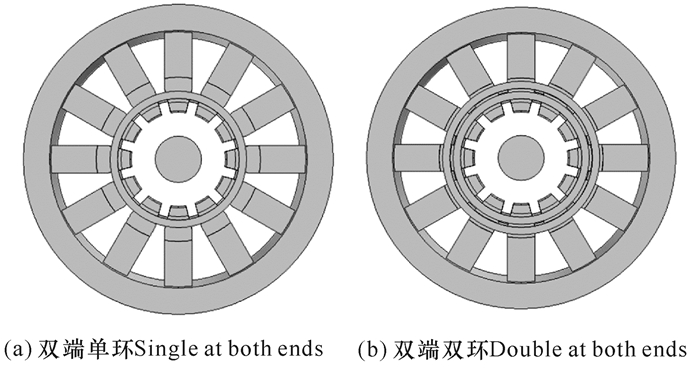
在磁控管阳极叶片的轴向底面分别引入单环或双环隔模带,带有隔模带磁控管的截面如图 3所示。对于双端单环的隔模带,轴向底面各有一个隔模带分别与相邻交错的阳极片相连接;对于双端双环的隔模带,轴向各有两个隔模带,连接方式与双端单环隔模带相同。
|
| 图 3 带有隔模带磁控管的截面图 Fig. 3 Schematic diagram of magnetron with strap |
1.2 热应力场分析
阳极叶片是磁控管中受热最多的部位,同时也是冷却散热的重要部件,阳极叶片的耐热能力直接影响谐振系统工作状态的稳定性,继而影响磁控管的寿命,因此对阳极叶片的热应力分析十分重要。本研究推导了扇形叶片和扇槽形叶片的温度公式并给出一种有效的散热水路设计。
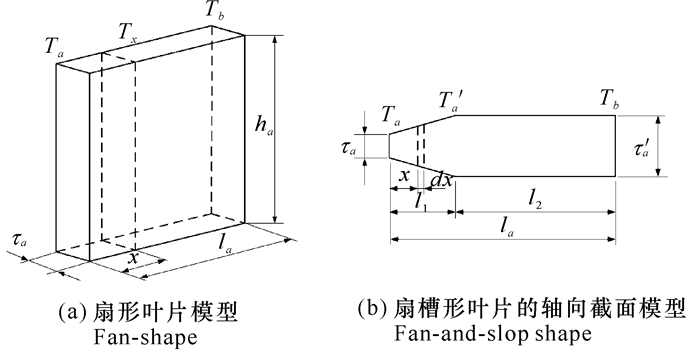
在磁控管正常工作时,互作用空间内的电子在电磁场的作用下对阳极叶片轰击,以及阳极工作面上高频电流流动产生的涡流热,使阳极温度升高发生形变,进而引起谐振腔谐振频率发生变化。谐振腔频率的变化或漂移会导致输出功率和效率的降低,影响工作的稳定性。单个扇形和扇槽形阳极叶片的模型如图 4所示。
|
| 图 4 阳极叶片模型 Fig. 4 Model of anode blade |
沿扇形阳极叶片径向的温度分布函数T(x)的微分方程可表示为
| $ $$S _ { \tau } \lambda \frac { \text{d} ^ { 2 } T ( x ) } { \text{d} x ^ { 2 } } = - \frac { \overline { P } _ { i n } } { N l _ { a } } ( 1 - \eta _ { c } ) \eta _ { e }, $$ $ | (6) |
其中,
| $ \begin{array}{l} \frac{{{\rm{d}}T(x)}}{{{\rm{d}}{x^2}}}{\rm{ = - }}\frac{{{{\bar P}_{in}}\left( {1 - {\eta _e}} \right)}}{{N{S_\tau }\lambda }}, x = 0时, \\ T\left( {{l_a}} \right){\rm{ = }}{T_b}, x = {l_a}时, \end{array} $ | (7) |
利用能量守恒定律,考虑边界条件(7),求解方程(6)得到扇形阳极叶片径向任意截面处的温度表达式
| $ \begin{array}{l} \;\;\;\;T(x) = {T_b} + \frac{{{l_a}{{\bar P}_{in}}}}{{N\lambda {S_\tau }}}\left( {1 - \frac{x}{{{l_a}}}} \right)[\left( {1 - {\eta _e}} \right) + \frac{1}{2}(1 - \\ {\eta _c}){\eta _e}\left( {1 + \frac{x}{{{l_a}}}} \right)], \end{array} $ | (8) |
当x=0时,得到阳极叶片工作面的温度Ta为
| $ {T_a}{\rm{ = }}{T_b} + \frac{{{l_a}{{\bar P}_{in}}}}{{N\lambda {S_\tau }}}\left( {1 - \frac{{\eta + {\eta _e}}}{2}} \right), $ | (9) |
其中,η=ηeηc是磁控管的总效率。
同理,按照上述推导扇形阳极叶片工作面温度的方法,得到扇槽形阳极叶片工作面温度Ta可表示为
| $ {T_a}{\rm{ = }}{T_b} + \frac{{{{\bar P}_{in}}}}{{N\lambda {S_\tau }}}\left[ {\left( {1 - {\eta _e}} \right){l_e} + \left( {{\eta _e} - \eta } \right)\frac{{{l_a}}}{2}} \right], $ | (10) |
其中,Sτ=haτa′,le是阳极叶片的等效长度,
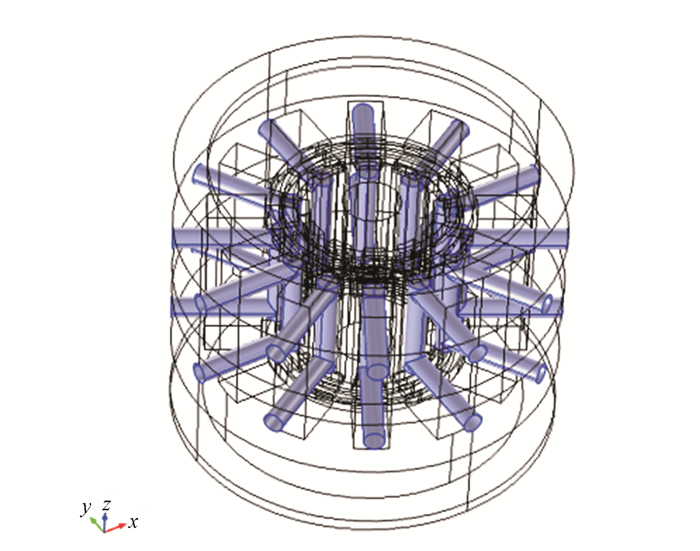
对输出功率大于1 kW的管子通常采取液冷方式,常用的液体是水。对于水冷的方式,一般情况下需要考虑冷却水的流动状态、流速、流量以及水路通道等关键因素。但为提高仿真的效率,这里将研究重点放在冷却水的冷却效果,冷却水本身并非研究对象。因此,通过设置水的温度和对流换热系数来模拟冷却效果,从而得到不同冷却条件下,谐振系统温度分布、热应力和形变,以及磁控管工作状态时谐振频率的变化。带有阳极冷却的冷却水路设计如图 5所示,阳极叶片内部“U”形水路增大阳极工作面和隔模带嵌入阳极部分的散热面积。
|
| 图 5 阳极叶片的“U”形水冷通道 Fig. 5 U-shaped water cooling channel of anode blade |
2 磁控管高频场与热应力场的仿真分析 2.1 扇槽形谐振系统的高频电磁场仿真
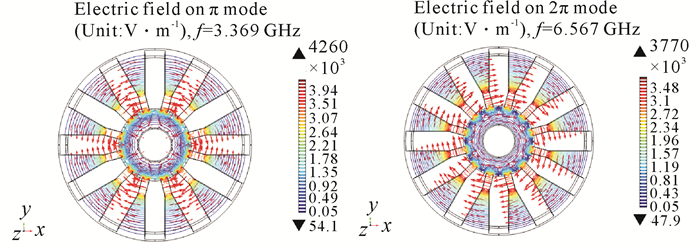
无隔模带谐振系统6个模式的谐振频率和品质因数如表 1所示。对于12腔的磁控管,除模式号为6的π模式,其它模式都是简并的,即每对模式具有相同的谐振频率和高频场分布结构。取前6个模式研究发现,π模式的模式分隔度为0.14%,这就使无隔模带磁控管的工作状态极不稳定,互作用空间的π模式高频场结构受到干扰和影响,电子流与π模式的相互作用程度减弱,输出功率和效率下降。这种情况下,必须添加隔模带以增大π模式与邻近模式的频率差别,使谐振系统稳定工作在π模式下。同时,谐振系统的品质因数随谐振频率的增大而下降,原因是阳极表面存在损耗,阳极的表面电阻随频率的上升而增大,导体边界的面损耗功率增大,总储能降低,谐振频率的上升趋势无法抵消总体能耗的降低,因此品质因数下降。图 6是谐振系统在π模式和2π模式下总的电场分布(轮廓线代表电场强度,箭头代表电场方向)。π模式和2π模式的电场分布不同,当磁控管工作在π模式时,相邻谐振腔的相位差为π;当磁控管工作在2π模式时,相邻谐振腔相位差为0(或2π)。
| 工作模式 Working modes |
谐振频率 Resonant frequencies f (GHz) |
品质因数 Quality factors Q |
| 1 | 2.622 | 2 950 |
| 2 | 3.157 | 2 889 |
| 3 | 3.294 | 2 801 |
| 4 | 3.344 | 2 748 |
| 5 | 3.364 | 2 717 |
| 6(π) | 3.369 | 2 708 |
|
| (a)π模式πmode(b)2π模式2πmode 图 6 谐振系统的电场分布 Fig. 6 Electric field distribution of resonant system |
从表 2中得出,双端单环隔模带磁控管谐振系统π模式工作状态下的模式分隔度为|(3.022-3.175)/3.022|×100%=5.1%,比无隔模带谐振系统π模式的模式分隔度有所提高。为保证磁控管工作的稳定性,工程上要求模式分隔度为15%~20%,所以双端单环隔模带仍无法满足要求。从表 3中得出,双端双环隔模带磁控管π模式的模式分隔度为|(2.409-3.406)/2.409|×100%=41.4%,模式分隔度有大幅度提高,能够满足工程要求。
| 工作模式 Working modes |
谐振频率 Resonant frequencies f (GHz) |
品质因数 Quality factors Q |
| 1 | 4.228 | 3 273 |
| 2 | 4.245 | 2 732 |
| 3 | 3.842 | 2 745 |
| 4 | 3.471 | 2 782 |
| 5 | 3.175 | 2 761 |
| 6(π) | 3.022 | 2 688 |
| 工作模式 Working modes |
谐振频率 Resonant frequencies f(GHz) |
品质因数 Quality factors Q |
| 1 | 4.594 | 1 217 |
| 2 | 5.806 | 1 458 |
| 3 | 5.671 | 1 283 |
| 4 | 4.868 | 1 014 |
| 5 | 3.406 | 968 |
| 6(π) | 2.409 | 1 951 |
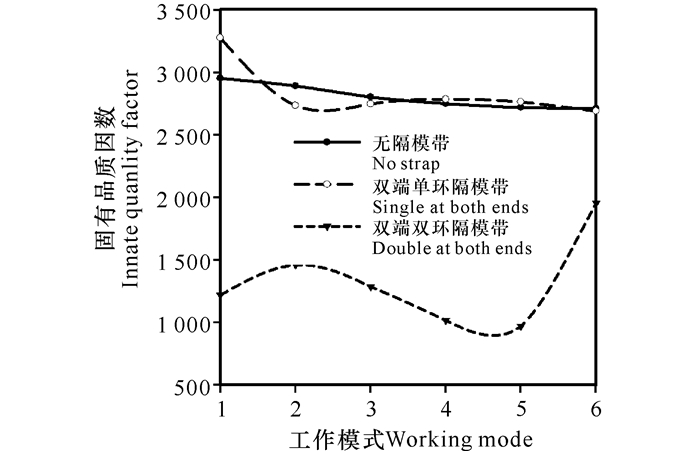
在无隔模带谐振系统中,固有品质因数与工作模式间的关系单一近似线性;加入隔模带后,不同工作模式下的品质因数波动起伏变大,在双端双环隔模带谐振系统中品质因数大幅下降(图 7)。这表明,隔模带的加入不仅使工作模式发生跳跃性变化(“跳模”现象),还改变了固有的谐振频率,增加了腔体的功率损耗,导致品质因数下降。因此,加入隔模带增大模式分隔度时,需要注意它对谐振频率和品质因数的影响。
|
| 图 7 磁控管谐振系统固有品质因数随工作模式的变化关系 Fig. 7 The relationship between the inherent quality factor of magnetron resonance system and the working mode |
2.2 磁控管热应力场仿真
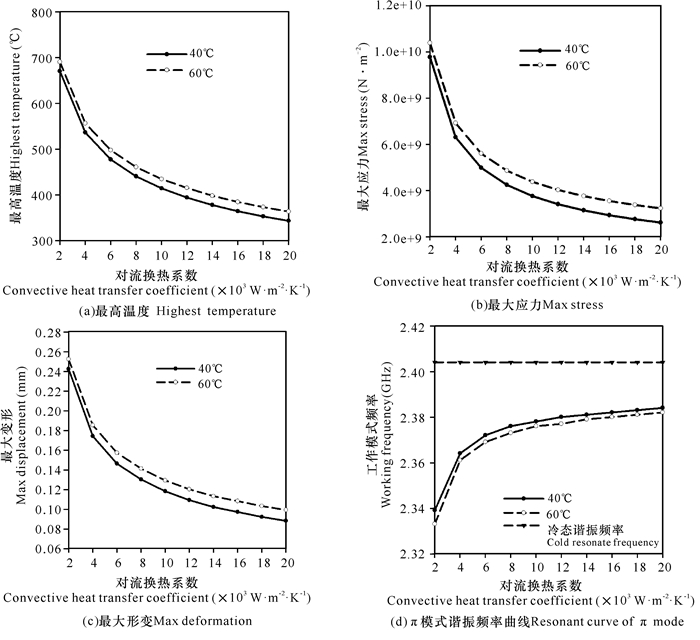
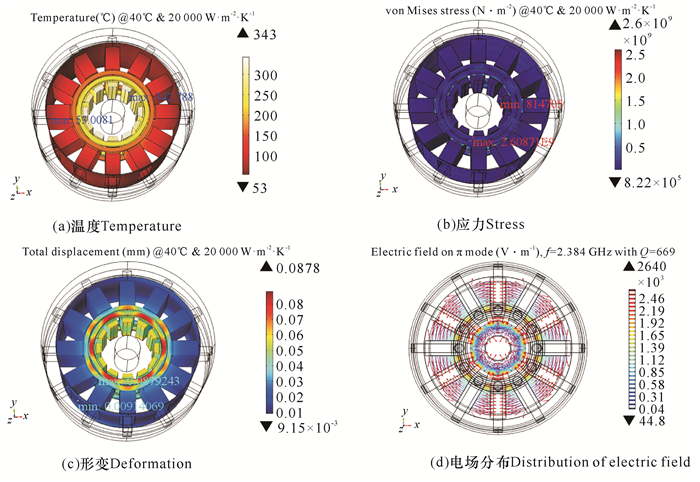
图 8给出冷却水分别在40℃和60℃时腔体谐振系统的最高温度、最大应力、最大形变以及谐振频率随冷却水对流换热系数的变化情况。冷却水温40℃、对流换热系数从2 000 W·m-2·K-1到6 000 W·m-2·K-1变化时,最高温度、最大应力和最大形变下降幅度较大,分别下降28.8%、48.9%和39.7%;图 9显示水冷40℃、对流换热系数20 000 W·m-2·K-1时各参量的变化情况,阳极叶片工作面温度最高达到343℃,冷却效果能够满足工程上的实际应用。然而,仿真结果显示谐振系统的品质因数由于热形变大幅下降,由此在对腔体进行冷却时不仅要考虑到阳极叶片温度,隔模带的热形变以及腔体的品质因数变化也需要进行计算。
|
| 图 8 水冷条件下谐振系统的各热力参数 Fig. 8 Thermal-stress parameters of resonant system with water cooling condition |
|
| 图 9 冷却水在40℃、20 000 W·m-2·K-1时谐振系统各参数分布 Fig. 9 The variation of the parameters of the resonant system with 40℃, 20 000 W·m-2·K-1 cooling water |
将该冷却水路的设计应用到输出功率30 kW、频率(2 450±25) MHz的连续波磁控管中,其实际使用场景如图 10所示。考虑到对阳极叶片工作面的冷却效果,根据水路通道的尺寸、入水和出水口的温度以及水流状态等, 得到实际应用下的冷却水流量应控制在≥19 L/min。

|
| 图 10 磁控管实际使用场景 Fig. 10 Actual use scene of magnetron |
2.3 热力场对谐振频率的影响
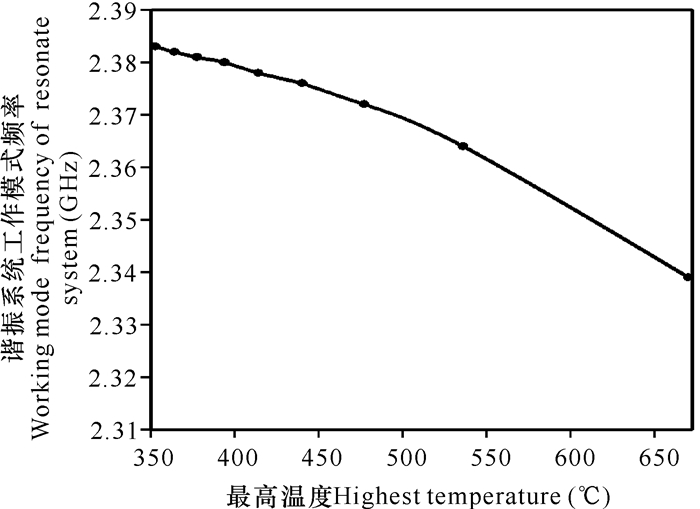
阳极叶片温度的改变会使磁控管的振荡频率产生一定程度的偏移,也就是频率的温度漂移。如图 11所示,π模式谐振频率随着阳极叶片温度的升高而减小,这主要是因为温度升高导致阳极叶片材料膨胀,腔体间隙变小,间隙电容变大,谐振频率降低。腔体部件最高温度每升高1℃,谐振频率下降0.137 MHz。磁控管谐振系统一般采用无氧铜制成,频率温度漂移比较大,如果对频率稳定性有较高的要求,可以在阳极材料中包裹钼等材料减小频率的温度漂移。
|
| 图 11 “U”形水冷条件下磁控管谐振系统的温度漂移曲线 Fig. 11 The thermal frequency drift curve of magnetron resonant system under "U" shaped water cooling condition |
3 结论
本研究梳理了一种用于大功率连续波磁控管腔体的高频电磁场-热应力耦合分析方法。针对提高磁控管工作稳定性和使用寿命的问题,首先对磁控管的谐振系统进行理论和仿真分析,运用等效电路理论计算谐振频率和模式分隔度,利用软件分析磁控管谐振系统在无隔模带、双端单环隔模带和双端双环隔模带情况下各个模式的谐振频率、模式分隔度和品质因数。虽然隔模带的加入能有效提高模式分隔度,但也会降低腔体的品质因数。其次对磁控管谐振系统进行热应力分析,分别给出扇形叶片和扇槽形阳极叶片工作面温度的计算方法;设计一种针对阳极叶片的“U”形散热水路,证明该设计能有效降低阳极温度、延长磁控管工作寿命。最后综合隔模带与冷却水路设计,分别在冷态和工作状态进行谐振腔的电磁与热耦合分析,得到谐振系统的热漂移曲线,对工程实践具有指导意义。
| [1] |
张兆镗. 磁控管的历史、现状与未来发展——兼论微波功率应用的前景[J]. 真空电子技术, 2016(2): 38-41. DOI:10.3969/j.issn.1002-8935.2016.02.010 |
| [2] |
丁耀根, 刘濮鲲, 张兆传, 等. 大功率微波真空电子器件的应用[J]. 强激光与粒子束, 2011, 23(8): 1989-1995. |
| [3] |
丁耀根, 刘濮鲲, 张兆传, 等. 真空电子学和微波真空电子器件的发展和技术现状[J]. 微波学报, 2010(1): 397-400. |
| [4] |
FENG T, GAO D P, ZHANG Z C.Thermal analysis of a high-power continuous wave magnetron cavity[C].2015 IEEE International Vacuum Electronics Conference (IVEC).Beijing, China: IEEE, 2015.
|
| [5] |
吴群. 磁控管的研究现状与发展趋势[J]. 哈尔滨工业大学学报, 2000, 32(5): 9-12. DOI:10.3321/j.issn:0367-6234.2000.05.003 |
| [6] |
李天明, 李家胤, 于秀云, 等. A6磁控管谐振系统的计算与模拟分析[J]. 强激光与粒子束, 2002, 14(3): 426-430. |
| [7] |
朱程, 杨金生, 李会成, 等. 30 kW连续波磁控管的研制[J]. 真空电子技术, 2013(5): 110-111. DOI:10.3969/j.issn.1002-8935.2013.05.030 |
| [8] |
姚列明.微波管的热分析[D].成都: 电子科技大学, 2006.
|
| [9] |
姚列明, 杨中海, 李斌, 等. 行波管收集极的热分析[J]. 强激光与粒子束, 2006, 18(1): 97-100. |
| [10] |
BAR-COHEN A, IYENGAR M. Design and optimization of air-cooled heat sinks for sustainable development[J]. IEEE Transactions on Components and Packaging Technologies, 2002, 25(4): 584-591. DOI:10.1109/TCAPT.2003.809112 |
| [11] |
YUE S, WANG W, ZHANG Z, et al.Simulation and experiment measurement of high power continuous wave magnetron[C].2016 IEEE International Vacuum Electronics Conference (IVEC).Monterey, CA, USA: IEEE, 2016: 1-2.
|
| [12] |
YUE S, ZHANG Z, GAO D. Theoretical investigation and simulation of resonant system of sector and hole-and-slot resonator type rising-sun magnetron[J]. IEEE Transactions on Plasma Science, 2015, 43(9): 3161-3167. DOI:10.1109/TPS.2015.2464111 |
| [13] |
SHI D F, QIAN B L, WANG H G, et al. Derivation and generalization of the dispersion relation of rising-sun magnetron with sectorial and rectangular cavities[J]. Physics of Plasmas, 2013, 20(12): 259-320. |
| [14] |
岳松, 张兆传, 高冬平. 无隔模带磁控管谐振系统的理论分析与仿真[J]. 电子与信息学报, 2014, 36(9): 2272-2277. |
| [15] |
岳松, 张兆传, 高冬平.隔膜带对磁控管谐振频率影响的三维仿真[C]//中国电子学会真空电子学分会第十九届学术年会论文集: 下册.北京: 中国电子学会真空电子学分会, 2013: 597-600.
|


