伊岭岩位于广西壮族自治区南宁市武鸣区,是一座典型的喀斯特岩溶洞。因附近的伊岭村而得名,壮语中又称为“敢宫”,其意为像宫殿一般美丽的岩洞。据地质学家推断,广西伊岭岩岩石形成于100万年前。伊岭岩岩石为钟乳石,主要成分为碳酸钙(CaCO3)。此外还含有少量的硅、铁、镁和微量的砷、锰、钛、铜、锶、钠等10多种元素[1]。在广西有“伊岭岩岩石入药治病”的说法,其中碳酸钙类矿物药是最具有代表性的一类[2]。到目前为止,碳酸钙是世界上存在最广泛的生物矿之一,对其生物矿化的研究也最普遍。在常温常压下,自然界中存在6种具有相同成分但结构不同的碳酸钙矿物,分别为无定形碳酸钙、单水碳酸钙、六水碳酸钙、球霰石、文石和方解石,其热力学稳定性按上述从无定形碳酸钙到方解石的顺序依次增加。这6种碳酸钙除了无定形碳酸钙,都是结晶体态。球霰石、文石、方解石是不含结晶水的碳酸钙晶体,其中方解石最稳定,文石和球霰石属于非稳态晶体[3]。表 1为球霰石、文石、方解石的晶格参数[4]。
扬州大学王晓明[5]通过调整碳酸钙晶体沉淀过程中Ca2+和K+的摩尔比,发现随着Ca2+/K+比值的增加,碳酸钙晶体由实心逐步转变为空心棒状,该实验结果有利于海水中生物矿化生成管状结构矿物的形成机理研究。浙江大学刘彦等[6]在碳酸钙中加入Na+后,发现碳酸钙的硫化转化率提高15%。这一研究结果使碳酸钙在脱硫处理方面的应用价值得到了提升,有利于环境保护。
目前从微观角度对碳酸钙的研究较少,基础数据的缺乏阻碍了碳酸钙矿石应用价值的提升。本文采用X射线衍射对广西伊岭岩岩石(CaCO3)进行晶体结构分析,利用电子显微镜及能谱分析伊岭岩岩石中包含的微量元素及其含量,采用Rietveld晶体结构精修方法研究微量元素在CaCO3晶体结构中占据的位置, 并运用德拜温度近似模型计算其德拜温度ΘD,用维氏硬度测量法测量广西伊岭岩岩石的硬度。本文开展的伊岭岩岩石(CaCO3)微观结构和性能研究,将为后续碳酸钙相关应用提供理论基础,并有利于碳酸钙矿物的开发及应用。
1 实验方法及拟合原理 1.1 方法实验所用的2块岩石样品为随机采集的广西伊岭岩岩石,分别标记为A1和A2(图 1)。

|
| 图 1 广西伊岭岩岩石A1和A2样品 Fig. 1 A1 and A2 samples of the Yilingyan rock in Guangxi |
首先取2个样品的一小部分用研磨钵研磨成粉末,然后装到载玻片上进行X射线衍射测试(日本理学Rigaku D/max-2500型衍射仪),Cu为衍射钯,Kα波长λ=1.540 6 Å,带有石墨单色器,普通快扫步长0.02,扫描速度8°/min,2θ扫描20°~80°,步进扫描10°~110°,扫描电压40 kV,扫描电流50 mA。采用计算机应用程序Jade5.0[7]对X射线衍射数据进行物相分析,再利用Fullprof软件[8-9]对步进扫描数据进行Rietveld全谱拟合分析,利用精修拟合结果得到温度因子,并根据德拜温度近似模型计算出2个样品的德拜温度。
另取一部分样品镶样,用带能谱的扫描电镜(日本日立SU-8020型场发射扫描电子显微镜)分析,观察样品的微观形貌及成分组成。再取一部分样品,经80#~1500#砂纸打磨后,在HXD-1000TM/LCD数字式显微硬度计上进行显微硬度测量,测量所用压头为正四棱锥形。为得到一个较为精确的结果,每个样品测试5次,去掉最大值和最小值,剩余3个取平均值作为最终结果。
1.2 Rietveld全谱图拟合法原理Rietveld全谱图拟合修正晶体结构的方法,是用最小二乘法来调节计算结构峰形参数与原子参数值, 依靠计算机程序逐点比较实验值的衍射强度和计算值的衍射强度,使计算值峰形与实验值峰形相匹配[10-11]。其方程为
| $ M = \sum {{W_i}{{\left[ {{Y_{{\rm{iobs}}}} - {Y_{{\rm{ical}}}}} \right]}^2}} , $ |
要求M达到最小值。Wi称为权重因子(即Wi=1/Yiobs),Yiobs为观察值((2θ)i衍射强度),Yical为计算值((2θ)i衍射强度)。
衍射强度的计算值Yical公式:
| $ \begin{array}{l} \;\;\;\;\;{Y_{{\rm{ical}}}} = s\sum\limits_K {{L_K}{{\left| {{F_K}} \right|}^2}\varphi \left( {2{\theta _i} - 2{\theta _k}} \right){P_K}{A^{ - 1}}{S_r}E + } {\rm{ }}\\ {Y_{{\rm{ib}}}}, \end{array} $ |
式中,s表示比例因子,LK包括Lorentz、多重性因子及偏振,FK为衍射K的结构因子,φ表示衍射K的线形函数,PK择优取向函数,A表示试样的吸收因子,Sr是关于试样表面粗糙度效应的函数,E表示消光因子,Yib表示点i处的衍射谱背底。Rietveld全谱图拟合修正结果可靠性主要由以下3个因子判断,RP、RWP、Rexp值越小,说明拟合结果越可靠。
(1) 图形剩余方差因子RP:
| $ {R_{\rm{P}}} = \sum {\left| {{Y_{{\rm{iobs}}}} - {Y_{{\rm{ical}}}}} \right|/\sum\limits_i {{Y_{{\rm{iobs}}}}} ;} $ |
(2) 权重图形剩余方差因子RWP:
| $ {R_{{\rm{WP}}}} = {\left\{ {\sum\limits_i {{W_i}{{\left( {{Y_{{\rm{iobs}}}} - {Y_{{\rm{ical}}}}} \right)}^2}/\sum\limits_i {{W_i}Y_{{\rm{iobs}}}^2} } } \right\}^{1/2}}; $ |
(3) 预期R因子Rexp:
| $ {R_{{\rm{exp}}}} = {\left[ {\left( {N - P} \right)/\sum\limits_i {{W_i}Y_{{\rm{iobs}}}^2} } \right]^{1/2}}。$ |
电子显微镜(SEM)可以清楚地观察样品的显微形貌和孔隙大小,是观察分析样品微观结构方便且易行的有效方法。能谱分析(EDS)是一种用来分析材料微区成分元素种类与含量的有效手段。通过SEM/EDS分析,可以直观地观察伊岭岩岩石表面形貌及其元素和含量,有利于对伊岭岩所含元素进行定量分析。
从图 2可以看出:2个样品的表面形貌相似,成分均匀。由于伊岭岩岩石较软,所以在制样过程中很难处理成光滑平面。如图 2所示,2个样品在电子显微镜下放大300倍时,表面凹凸不平且带有光泽。利用SEM观察很难分辨出二者的区别。

|
| 图 2 A1、A2样品的SEM图 Fig. 2 SEM image of A1 and A2 samples |
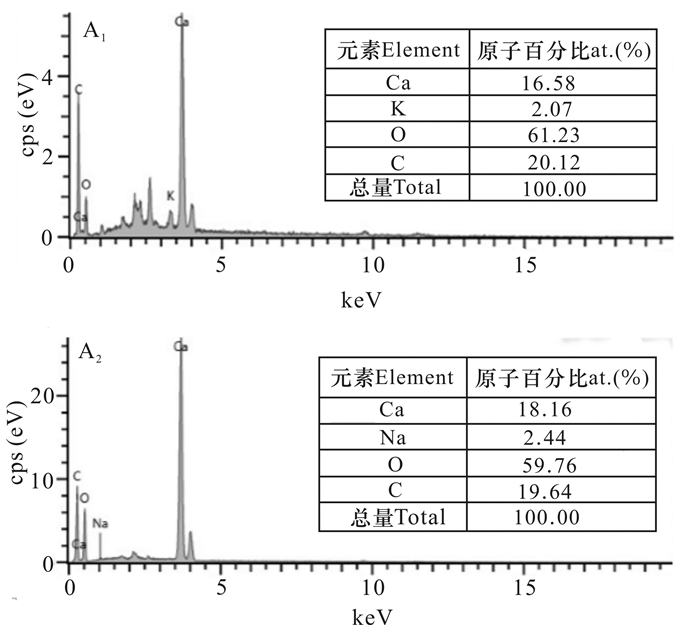
分别对2个样品进行能谱测试,结果如图 3和表 2所示,2个样品的主要成分分别为Ca16.58K2.07C20.12O61.23、Ca18.16Na2.44C19.64O59.76,均为CaCO3。二者分别存在微量的K+和Na+,其原子百分比分别为2.07%、2.44%。
|
| 图 3 A1、A2样品的EDS图 Fig. 3 EDS image of A1 and A2 samples |
| 元素 Element |
A1 | A2 | |||
| 重量百分比 wt.(%) |
原子百分比 at.(%) |
重量百分比 wt.(%) |
原子百分比 at.(%) |
||
| Ca | 50.92 | 16.58 | 49.31 | 18.16 | |
| K | 1.93 | 2.07 | - | - | |
| Na | - | - | 4.83 | 2.44 | |
| O | 36.89 | 61.23 | 32.75 | 59.76 | |
| C | 10.26 | 20.12 | 13.11 | 19.64 | |
| 总量Total | 100.00 | 100.00 | 100.00 | 100.00 | |
2.2 晶体结构
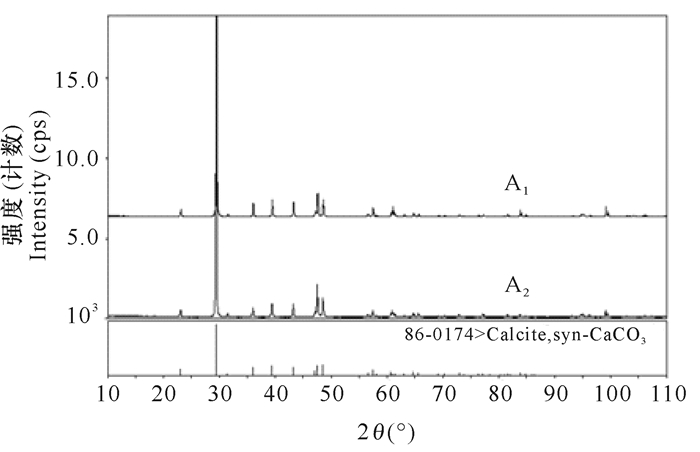
由于碳酸钙具有同分异构的特点,故对伊岭岩岩石进行X射线衍射分析,有助于直接对组成伊岭岩的碳酸钙种类进行辨别,对后期深入研究碳酸钙矿石形成的动力学机制具有理论和实际意义。A1、A2样品X射线衍射分析后,其衍射图谱如图 4所示。利用Jade 5.0计算机程序对衍射数据进行物相分析,结果表明A1、A2样品的相组成相同,都是由单相的CaCO3组成,属于密排六方结构,其空间群为R3C(No.167),属于典型的方解石。除CaCO3外,在XRD图谱中没有观察到其他衍射峰。
|
| 图 4 样品A1、A2的XRD图谱 Fig. 4 XRD patterns of samples A1 and A2 |
为了详细地了解伊岭岩岩石中CaCO3的晶体结构,本研究采用步进扫描方式收集样品的XRD数据。利用Jade5.0对步进扫描数据进行指标化,得到其点阵参数a=b=4.988 Å,c=17.068 Å。将得到的CaCO3晶体结构数据作为初始数据,分别用K+和Na+替代部分Ca2+位置,输入到fullprof计算机程序中进行Rietveld全谱拟合分析。采用Pesudo-Voigt函数作为峰形函数。分析过程中,共修正了25个参数,包括点阵参数、半峰宽、择优取向因子、离子位置和各向同性温度因子等。
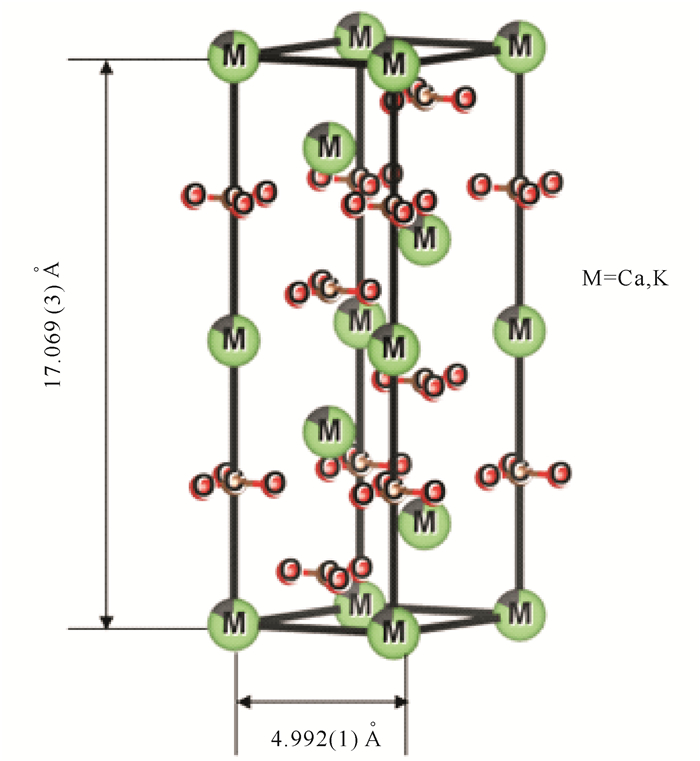
图 5为A1样品的XRD数据观察值、计算值和残差。表 3为A1样品精修后的原子占位、占有率及温度因子。由表 3可知,A1样品的实际晶格常数为a=b=4.992(1) Å,c=17.069(3) Å。所有K+与Ca2+共同占据了6b(0,0,0)的位置。K+替代了部分Ca2+,且K+占21%,Ca2+占79%。C原子单独占据6a(0,0,1/4)位置,O原子单独占据18e(1/4,0,1/4)的位置。精修后的晶格常数a、b、c比标准方解石型CaCO3的晶格常数大,这是由于半径较大的K+(RK=2.27 Å)替代了Ca2+(RCa=1.97 Å),使得晶格发生了膨胀。图 6是A1号样品根据精修得到的原子占位画出的晶体结构。表 4列出了A1样品晶体结构中部分原子间距,其中Ca—C、Ca—O、C—O键长分别为4.986 Å、2.376 Å、1.246 Å。

|
| 图 5 A1样品的XRD精修拟合图谱 Fig. 5 XRD rietveld refinement results for A1 sample |
| 原子 Atoms |
位置 Sites |
x | y | z | 晶格参数 Lattice parameters (Å) |
原子占位 Atomic occupancy |
温度因子 Temperature factor Beq(Å2) |
可靠性因子 Reliability factors |
||||
| a | b | c | RP | RWP | RE | |||||||
| Ca | 6b | 0 | 0 | 0 | 0.79 | 0.457 2(7) | ||||||
| K | 6b | 0 | 0 | 0 | 4.992(1) | 4.992(1) | 17.069(3) | 0.21 | 0.457 2(7) | 0.092 | 0.101 | 0.024 |
| C | 6a | 0 | 0 | 1/4 | 1 | 0.016 8(6) | ||||||
| O | 18e | 1/4 | 0 | 1/4 | 1 | 0.062 1(0) | ||||||
|
| 图 6 A1样品Ca1-xKxCO3(x=0.21)的晶体结构 Fig. 6 Crystal structure of the Ca1-xKxCO3(x=0.21)in sample A1 |
| 原子键 Atomic bond |
原子间距(Å) Atomic distance (Å) |
原子键个数 Number of atomic bonds |
| M—C | 4.986 51 | ×2 |
| M—O | 2.376 31 | - |
| C—O | 1.246 62 | ×3 |
| Note:M=Ca,K | ||
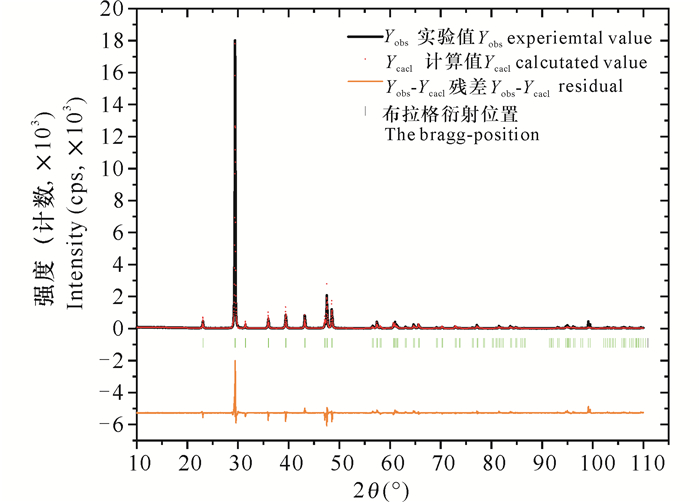
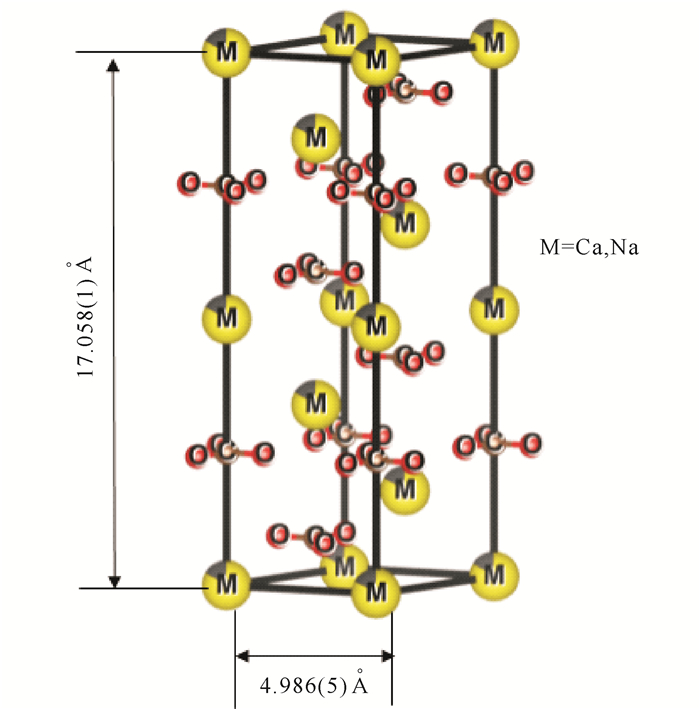
A2样品的XRD数据观察值、计算值和残差如图 7所示。精修后的原子占位、占有率及温度因子列见表 5。由表 5可知,类似A1样品,在A2样品中CaCO3为主要物相。精修得到的晶格常数为a=b=4.986(5) Å,c=17.058(1) Å。由Na+和Ca2+共同占据6b(0,0,0)的位置,且Na+占18%,Ca2+占82%。C原子单独占据6a(0,0,1/4)的位置,O原子单独占据18e(1/4,0,1/4)的位置。精修后的点阵参数与标准方解石型CaCO3晶格常数略小,单胞体积减小。这是因为部分Na+(RNa=1.86 Å)替代了CaCO3晶体结构中Ca2+(RCa=1.97 Å)的位置。图 8是A2样品根据精修得到的原子占位画出的晶体结构,表 6列出了A2样品晶体结构中的部分原子间距。其中Ca—C、Ca—O、C—O键长分别为4.697 62 Å、2.336 45 Å、1.226 18 Å。
|
| 图 7 A2样品的XRD精修拟合图谱 Fig. 7 XRD rietveld refinement results for A2 sample |
| 原子 Atoms |
位置 Sites |
x | y | z | 晶格参数 Lattice parameters(Å) |
原子占位 Atomic occupancy |
温度因子 Temperature factor Beq(Å2) |
可靠性因子 Reliability factors |
||||
| a | b | c | RP | RWP | RE | |||||||
| Ca | 6b | 0 | 0 | 0 | 0.82 | 0.456 9(6) | ||||||
| Na | 6b | 0 | 0 | 0 | 4.986(5) | 4.986(5) | 17.058(1) | 0.18 | 0.456 9(6) | 0.081 | 0.924 | 0.031 |
| C | 6a | 0 | 0 | 1/4 | 1 | 0.026 7(1) | ||||||
| O | 18e | 1/4 | 0 | 1/4 | 1 | 0.056 3(3) | ||||||
|
| 图 8 A2样品Ca1-xNaxCO3(x=0.18)的晶体结构 Fig. 8 Crystal structure of the Ca1-xNaxCO3(x=0.18)in sample A2 |
| 原子键 Atomic bond |
原子间距 Atomic distance (Å) |
原子键个数 Number of atomic bonds |
| M-C | 4.697 62 | ×2 |
| M-O | 2.336 45 | - |
| C-O | 1.226 18 | ×3 |
| Note:M=Ca,Na | ||
2.3 德拜温度
德拜温度ΘD是材料重要的热力学性质,是晶体具有的固定特征值,反映原子间结合力及原子振动情况。根据德拜温度近似模型计算伊岭岩的热力学稳定性,探讨其原子间的结合力以及力学性能,有助于了解碳酸钙矿石的形成机理。A1样品Ca1-xKxCO3(x=0.21)的德拜温度ΘD与晶体内各原子的温度因子BCa、BK、BC、BO满足以下关系[12]:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\frac{1}{{36}}[6\left( {\frac{{79}}{{100}}{\rm{ }}{m_{{\rm{Ca}}}}{B_{{\rm{Ca}}}} + \frac{{21}}{{100}}{\rm{ }}{m_{\rm{K}}}{B_{\rm{K}}}} \right) + 6{m_{\rm{C}}}{B_{\rm{C}}} + \\ {\rm{ }}18{m_{\rm{O}}}{B_{\rm{O}}}] = {\rm{ }}\frac{{6{h^2}T}}{{k\mathit{\Theta }_{\rm{D}}^2}}{\rm{ }}\left\{ {\mathit{\Phi }\left( x \right) + \frac{x}{4}{\rm{ }}} \right\}, \end{array} $ | (1) |
式(1)中x= ΘD/T,h为普朗克常量,k为玻尔兹曼常数,T为实验温度,Φ(x)为德拜函数,其定义如下:
| $ \mathit{\Phi }\left( x \right) = \frac{1}{x}\int_0^x {\frac{y}{{{e^y} - 1}}{{\rm{d}}_y}, } $ | (2) |
令
| $ \begin{array}{l} \;\;\;\;\;\;G = {\rm{ }}\frac{{kT}}{{216{h^2}}}[6\left( {\frac{{79}}{{100}}{\rm{ }}{m_{{\rm{Ca}}}}{B_{{\rm{Ca}}}} + \frac{{21}}{{100}}{m_{\rm{K}}}{B_{\rm{K}}}} \right) + \\ {\rm{ }}6{m_{\rm{C}}}{B_{\rm{C}}} + 18{m_{\rm{O}}}{B_{\rm{O}}}], \end{array} $ | (3) |
则方程(1)可以简化为
| $ \mathit{\Phi }\left( x \right) + \frac{x}{4} = G{x^2}。$ | (4) |
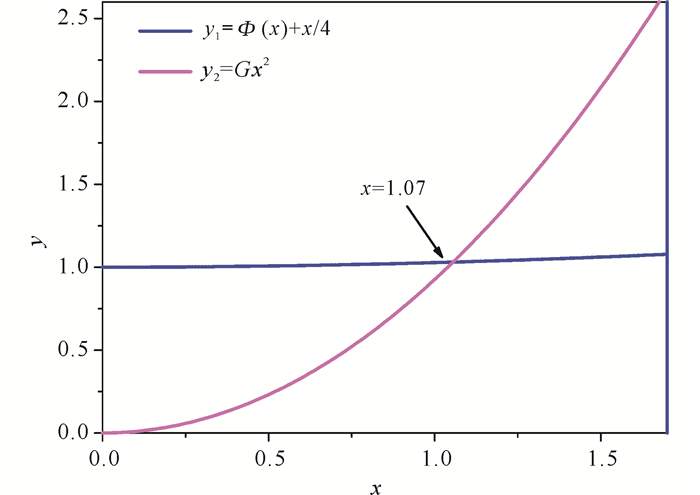
把A1样品Rietveld精修得到的表 2中的各原子温度因子BCa、BK、BC、BO代入(3)中可以得到G=0.862,再把G值代入(4),画出y1=Φ(x)+x/4和y2=Gx2两条曲线, 如图 9所示。求出2条曲线的交点x=1.07,即当x=1.07时,式(4)成立。根据x=ΘD/T,可以得到Ca1-xKxCO3(x=0.21)的德拜温度约为ΘD = Tx=318.86 K。
|
| 图 9 利用德拜近似模型计算A1样品的德拜温度ΘD Fig. 9 Calculating the Debye temperature (ΘD) of the A1 sample using the Debye approximation model |
同理,利用德拜温度近似模型,可以计算A2样品Ca1-xNaxCO3(x=0.18)的德拜温度ΘD,其中德拜温度ΘD与晶体内各原子的温度因子BCa、BNa、BC、BO满足以下关系:
| $ \begin{array}{l} \;\;\;\;\frac{1}{{36}}[6\left( {\frac{{41}}{{50}}{\rm{ }}{m_{{\rm{Ca}}}}{B_{{\rm{Ca}}}} + \frac{9}{{50}}{\rm{ }}{m_{{\rm{Na}}}}{B_{{\rm{Na}}}}} \right) + 6{m_{\rm{C}}}{B_{\rm{C}}} + \\ 18{m_{\rm{O}}}{B_{\rm{O}}}] = \frac{{6{h^2}T}}{{k\mathit{\Theta }_{\rm{D}}^2}}\left\{ {\mathit{\Phi }\left( x \right) + \frac{x}{4}} \right\}{\rm{, }} \end{array} $ | (5) |
| $ \begin{array}{l} \;\;\;\;\;G = \frac{{kT}}{{216{h^2}}}[6\left( {\frac{{41}}{{50}}{m_{{\rm{Ca}}}}{B_{{\rm{Ca}}}} + \frac{9}{{50}}{m_{{\rm{Na}}}}{B_{{\rm{Na}}}}} \right) + \\ 6{m_{\rm{C}}}{B_{\rm{C}}} + 18{m_{\rm{O}}}{B_{\rm{O}}}]。\end{array} $ | (6) |
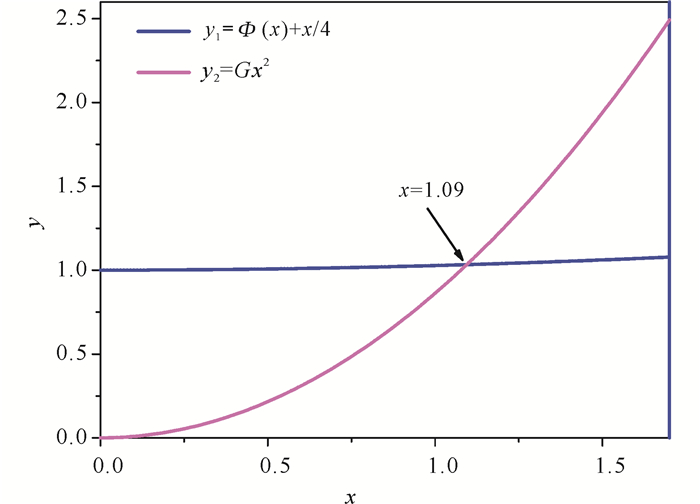
把A2样品Rietveld精修得到的表 5中的各原子的温度因子BCa、BNa、BC、BO代入(6)中可以得到G=0.871,再把G值代入(4),画出y1=Φ(x)+x/4和y2=Gx2两条曲线, 如图 10所示。求出2条曲线的交点x=1.09,即当x=1.09时,式(4)成立。根据x=ΘD/T,可以得到Ca1-xNaxCO3(x=0.18)的德拜温度约为ΘD = Tx = 324.82 K。
|
| 图 10 利用德拜近似模型计算A2样品的德拜温度ΘD Fig. 10 Calculating the Debye temperature (ΘD) of the A2 sample using the Debye approximation model |
A2样品的德拜温度比A1样品高,主要由于Na原子最外层电子受到原子核的约束力比K原子最外层电子受到的约束力要大,失去电子需要的能量较多,则原子键结合力强,德拜温度高。由德拜温度的物理意义可知,德拜温度越高,原子间作用力越大,膨胀系数越小,杨氏模量越大。所以A2样品的原子间作用力比A1样品大,膨胀系数比A1小,杨氏模量比A1大。
2.4 硬度测试矿物的硬度是矿物的重要物理常数和鉴定标志。某些矿物硬度的细微变化常与形成条件有关,因此根据硬度可以探讨矿物的成因。伊岭岩岩石硬度偏软,但是在不同岩石区域,硬度也会有所不同,可以通过硬度测试来探讨伊岭岩岩石的形成时间及相关条件。由于维氏硬度具有检测范围宽、压痕较小等特点,本实验采用维氏硬度测量A1、A2样品的维氏硬度。通过测量压痕的大小对维氏硬度进行计算,计算公式如下:
| $ {\rm{HV}} = 0.102 \times \frac{F}{S} = 0.102 \times \frac{{2F{\rm{sin}}\frac{\alpha }{2}}}{{{d^2}}}, $ | (7) |
其中F为试验载荷,单位为N;S为压痕面积,单位为mm2;α为相对面夹角136°;d为压痕对角线的长度,单位为mm。
表 7为A1、A2样品的维氏硬度值,可以发现,A2样品的硬度大于A1,这可用前面精修拟合结果解析。因为R(K)>R(Na),所以A2样品中晶粒小于A1样品中的晶粒大小,A2样品中的Na+对伊岭岩岩石有明显的细化作用,导致在受应力时位错运动受阻,从而硬度较大[13]。同时也可能是Na原子半径较小,原子间间距较小,原子间作用力加强,所以硬度较大。通过试样显微硬度的标准差可以近似反映试样的晶粒均匀性。由表 7可知,A1、A2样品的标准差都非常小,说明2个样品晶粒分布均匀,但A2样品的均匀性优于A1。
| 样品名称 Sample name |
显微硬度 Microhardness (HV) |
|
| 平均值 Average value |
标准差 Standard deviation |
|
| A1 | 132.6 | 2.6 |
| A2 | 148.9 | 2.2 |
3 结论
利用XRD及SEM/EDS技术分析了广西伊岭岩岩石,岩石的主要成分为CaCO3,A1样品中包含少量的K+,A2样品中包含少量Na+。主要物相CaCO3属于密排六方结构,其空间群为R3C(No.167),晶格常数a=b=4.988 Å,b=17.068 Å。K+替代了A1样品主要物相CaCO3中的Ca2+,使得其点阵参数变大,单胞体积变大。同样A2样品中的Na+替代了样品中CaCO3中的Ca2+位置,造成了A2中的CaCO3点阵参数变小,单胞体积变小。A1样品的德拜温度为318.86 K,A2样品的德拜温度为324.82 K。A2样品的原子间作用力比A1样品大,膨胀系数比A1小,杨氏模量比A1大。通过维氏硬度测试确定A2样品的硬度大于A1,且2个样品晶粒分布均匀,但A2样品的均匀性优于A1。
| [1] |
赵中杰. 矿物药分析[M]. 北京: 人民卫生出版社, 1991.
|
| [2] |
杨丽, 李雪莲, 赵梓辰, 等. 差热分析法鉴别碳酸钙类矿物药的研究[J]. 时珍国医国药, 2014, 25(10): 2412-2414. |
| [3] |
HAN Y S, HADIKO G, FUJI M, et al. Crystallization and transformation of vaterite at controlled pH[J]. Journal of Crystal Growth, 2006, 289(1): 269-274. DOI:10.1016/j.jcrysgro.2005.11.011 |
| [4] |
刘庆峰, 尚文宇, 王茁, 等. 晶须碳酸钙的制备和结构特性[J]. 硅酸盐通报, 2000(4): 13-16. DOI:10.3969/j.issn.1001-1625.2000.04.003 |
| [5] |
王晓明.Mg2+、K+协同作用下文石晶体的生长[D].扬州: 扬州大学, 2011.
|
| [6] |
刘彦, 周俊虎, 赵晓辉, 等. Na2CO3对O2/CO2气氛下CaCO3固硫特性的影响研究[J]. 高校化学工程学报, 2005, 19(2): 263-267. DOI:10.3321/j.issn:1003-9015.2005.02.023 |
| [7] |
Materials Date Inc.XRD Pattern Processing[CP].2002.
|
| [8] |
ROISNEL T, RODRIGUEZ-CARVAJAL J. Win-PLOTR:A windows tool for powder diffraction pattern analysis[J]. Materials Science Forum, 2001, 378/379/380/381: 118-123. |
| [9] |
RODRIGUEZ-CARVAJAL J. FullProf:A program for rietveld retinement and profile matching analysis of complex powder diffraction patterns[J]. Physica B, 1993, 44(193): 55-69. |
| [10] |
ZENG L M, LIAO J P, QIN P L, et al. Phase relations in the Al-Pr-Sb system at 773 K[J]. Journal of Alloys and Compounds, 2008, 450(1/2): 252-254. |
| [11] |
徐光宪. 稀土:上册[M]. 北京: 冶金工业出版社, 1995.
|
| [12] |
HE W, YANG T H, LIU H R, et al. Crystal structure and electrical resistivity of ZrAg0.46Al2.54[J]. ITMS, 2015, 15(346): 1492-1495. |
| [13] |
杨迪. 金属硬度试验[M]. 北京: 计量出版社, 1983.
|



