MnBi合金存在多种相结构,包括高温相(HTP)、低温相(LTP)、淬火高温相(QHTP)等。其中高温相(HTP)具有优异的磁光特性,低温相(LTP)属于NiAs型晶体结构,具有很高的磁晶各向异性[1]。MnBi合金的矫顽力随温度的增加而增加,在400 K时达到最大(2.0 T),此时,最大磁能积达到4.6 MGOe[2]。MnBi的铁磁性能主要来源于其低温相,但是合金在常温下可以形成多个紧密联系的相,如低温相、高温相等。这给制备高纯度MnBi合金低温相带来了极大的困难,从而在很大程度上制约了MnBi合金的发展。
MnBi合金具有许多特殊的磁性能,例如高矫顽力、高磁能积等永磁性能以及显著的磁光特性和磁致伸缩效应等[3-5],因此受到研究者们的广泛关注。MnBi合金有较高的热磁输入和清除性能,经常被当作磁光材料。MnBi具有正的矫顽力温度系数[6],在高温下的矫顽力比它在常温下时大大提高,因此可将其应用在高温环境下。MnBi系合金有望成为磁性能较好的高温应用磁性材料。近年来,关于MnBi合金的研究越来越受关注,前人在制备单相MnBi合金方面已经做了很多努力[7],但一直还没有成功通过Mn、Bi单质制备出单相的MnBi合金[8-9],目前的研究主要集中在通过改进制备技术、制备工艺及掺杂的方式来提高LTP-MnBi含量和合金的磁性能[10]。
本文主要研究MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)系列合金样品的晶体结构、磁性能及德拜温度,旨在为MnBi基无稀土永磁体的研发和应用提供参考依据。
1 材料与方法以纯度均为99.99%的Mn、Bi和Cr金属单质为原料,按照MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)的成分进行配料。由于Mn在高温下易挥发,故而需对Mn进行补熔损。本研究以多加5%的Mn进行补损。采用真空电弧熔炼制备MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)的合金。为保证试样的均匀性,每个试样需反复熔炼4次。由于熔融温度高于各组分的熔点,容易引起偏析造成成分不均匀,故必须进行均匀化退火。本研究将真空熔炼所得到的合金热处理后利用X射线衍射(XRD)、扫描电子显微镜(SEM)以及振动样品磁强计(VSM)对样品进行物相分析、晶体结构分析及磁性能分析。
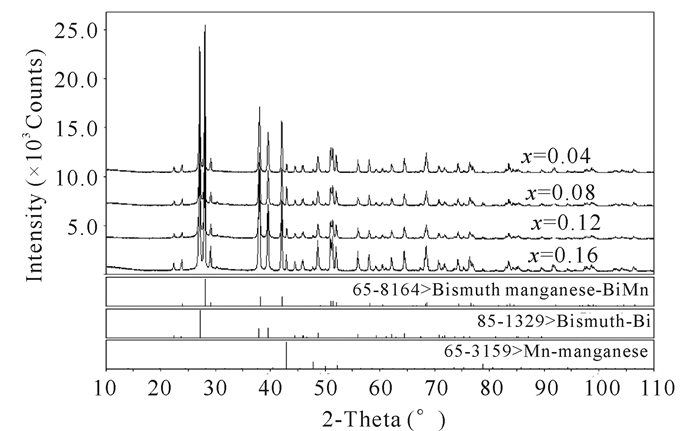
2 结果与分析 2.1 物相分析和晶体结构分析从图 1可以看出,MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)系列合金样品退火后主相为MnBi低温相,空间群为P63/mmc(194),同时还含有少量的Bi相,空间群为R3m(166),以及少量Mn相,空间群为I43m(217)。
|
| 图 1 MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)系列样品的X射线衍射图谱 Fig. 1 X-ray diffraction pattern of MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16) series samples |
利用Jade5.0软件对样品的X射线衍射数据进行指标化,将低温相MnBi(空间群为P63/mmc(194))的晶体结构参数作为初始数据,其中用Cr原子替代部分Bi原子位置,输入到计算机程序Maud。其中拟合修正的峰型函数为pseudo-Voigt函数。分析过程中,共修正了25个参数,包括点阵参数、半峰宽、择优取向因子、离子位置和各向同性温度因子等。最终得到MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)系列合金样品的Rietveld全谱图。精修结果的可靠性由图形剩余方差因子Rp和权重图形剩余方差因子RWP体现,其表达式为
| $ \begin{array}{*{20}{l}} {{R_{\rm{P}}} = \frac{{\sum | {Y_i}({\rm{ obs }}) - {Y_i}({\rm{ calc }})}}{{\sum {{Y_i}} ({\rm{ obs }})}}}\\ {{R_{{\rm{wP }}}} = {{\left\{ {\frac{{\sum {{\omega _i}} {{\left[ {{Y_i}({\rm{ obs }}) - {Y_i}({\rm{calc}})} \right]}^2}}}{{\sum {{\omega _i}} \left[ {{Y_i}({\rm{ obs ) }}{]^2}} \right.}}} \right\}}^{1/2}}, } \end{array} $ |
RP、RWP值越小,说明拟合结果越可靠。
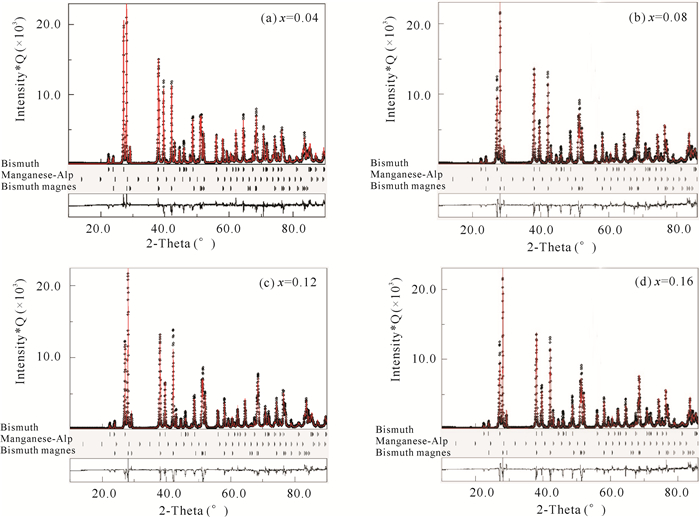
图 2为MnBi1-xCrx系列合金样品的Rietveld精修拟合图谱,从图谱中可以观察到实验值、计算值和残差。通过残差的大小可以判断拟合效果。样品的精修拟合结果如表 1所示。可以发现掺杂后并未改变样品中各物相的晶体结构,只是在LTP-MnBi晶体结构中晶胞参数发生了变化,随着掺杂量的增加,LTP-MnBi的晶格常数a逐渐减小,c基本保持不变。这是由于Cr原子半径(1.27 Å)比Bi原子半径(1.70 Å)小,Cr原子取代Bi原子造成LTP-MnBi发生晶格畸变。同时还可发现MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)系列合金样品中都是以LTP-MnBi相为主相,含量在73%以上。值得一提的是,由于Bi的熔点只有544.52 K,沸点为(18 330±50) K,真空电弧熔炼炉无法精确控制温度,故在制备样品的时候,Bi极易析出,以单质留在合金当中。所以在本研究中,所有的样品都含有Bi相。这和Pirich等[9]、Kang等[10]研究结果一致。MnBi1-xCrx系列合金样品中LTP-MnBi的键类型、原子间距、键的个数如表 3所示。在MnBi1-xCrx化合物的点阵中,与M(M=Bi,Cr)原子最近邻的M原子的个数是3。它们之间的原子间距dM-M随着掺杂量增大而增大。与M原子最近邻的Mn原子的个数是4,它们之间的原子间距dM-Mn随着掺杂量增大而减小。
|
| 图 2 MnBi1-xCrxRietveld拟合精修的结果 Fig. 2 Rietveld refinement results for MnBi1-xCrx |
| 掺杂含量 Doping content x |
相 Phase |
空间群 Space group |
晶胞参数 Lattice parameters (Å) |
质量分数 Weight fractions (%) |
可靠性因子 Reliability factors |
||||
| a | b | c | RP | RWP | Rexp | ||||
| 0.04 | MnBi1-xCrx | P63/mmc | 4.287 96 | 4.287 96 | 6.119 44 | 77.21 | 0.128 | 0.155 | 0.058 |
| Bi | R3m | 4.546 81 | 4.546 81 | 11.864 05 | 9.82 | ||||
| Mn | I43m | 8.913 38 | 8.913 38 | 8.913 38 | 13.97 | ||||
| 0.08 | MnBi1-xCrx | P63/mmc | 4.283 54 | 4.283 54 | 6.114 25 | 77.18 | 0.161 | 0.203 | 0.057 |
| Bi | R3m | 4.542 12 | 4.542 12 | 11.855 11 | 12.14 | ||||
| Mn | I43m | 8.899 27 | 8.899 27 | 8.99 27 | 10.68 | ||||
| 0.12 | MnBi1-xCrx | P63/mmc | 4.287 66 | 4.287 66 | 6.131 56 | 75.23 | 0.165 | 0.183 | 0.081 |
| Bi | R3m | 4.546 38 | 4.546 38 | 11.862 45 | 16.11 | ||||
| Mn | I43m | 8.920 49 | 8.920 49 | 8.920 49 | 8.66 | ||||
| 0.16 | MnBi1-xCrx | P63/mmc | 4.290 13 | 4.290 13 | 6.117 18 | 73.96 | 0.173 | 0.186 | 0.061 |
| Bi | R3m | 4.548 24 | 4.548 24 | 11.865 93 | 17.25 | ||||
| Mn | I43m | 8.915 29 | 8.915 29 | 8.915 29 | 8.79 | ||||
| 掺杂含量 Doping content x |
键类型 Bond type* |
键长 Distance(Å) |
数量 Quantity |
| 0.04 | M-M | 3.056 70(1) | ×3 |
| M-Mn | 2.908 75(1) | ×4 | |
| Mn-Mn | 3.932 99(3) | - | |
| 0.08 | M-M | 3.056 95(2) | ×3 |
| M-Mn | 2.908 13(2) | ×4 | |
| Mn-Mn | 3.932 67(1) | - | |
| 0.12 | M-M | 3.057 40(4) | ×3 |
| M-Mn | 2.907 81(1) | ×4 | |
| Mn-Mn | 3.932 70(6) | - | |
| 0.16 | M-M | 3.057 65(5) | ×3 |
| M-Mn | 2.907 63(4) | ×4 | |
| Mn-Mn | 3.932 71(1) | - | |
| Note:*M=Bi, Cr | |||
2.2 磁性能分析
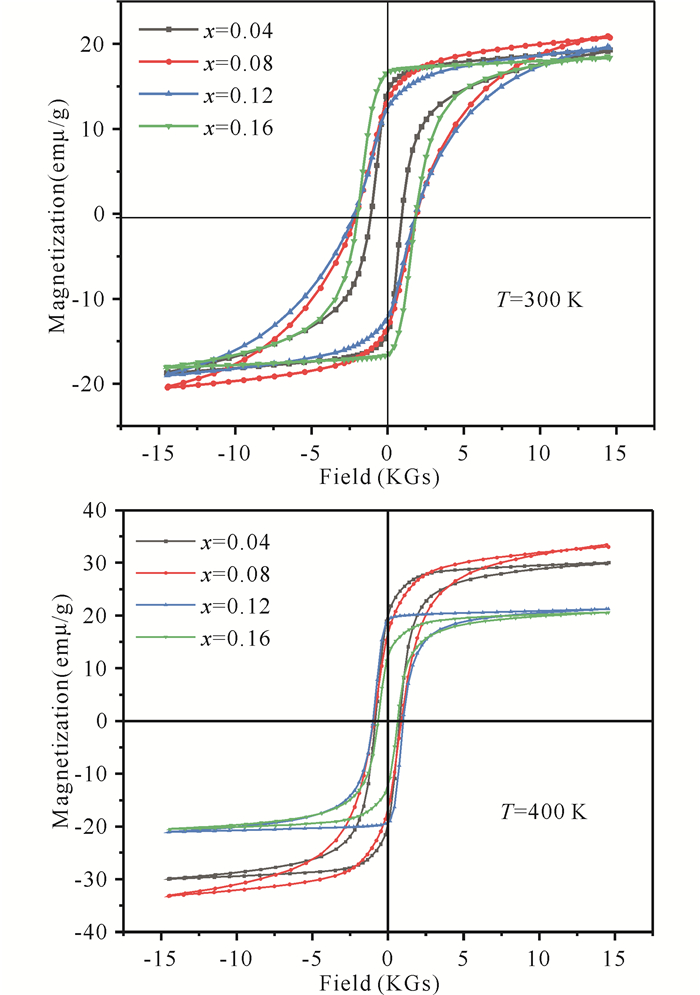
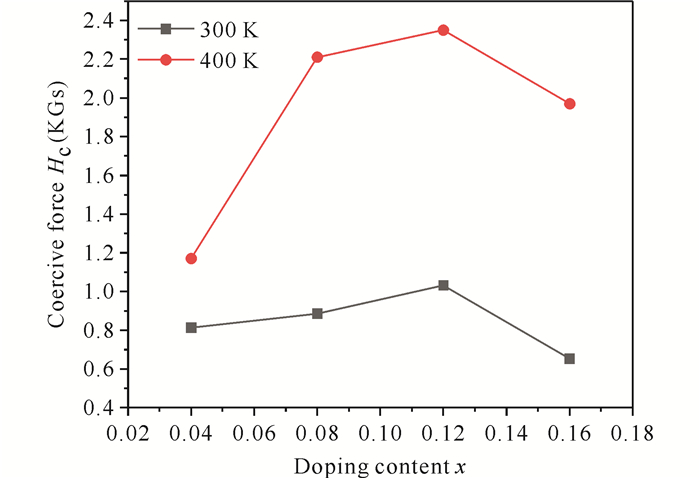
本研究利用振动样品磁强计(VSM)分别测试了合金MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)在300 K及400 K时磁矩随外场的变化关系。从图 3可知,合金在300 K与400 K温度下均为铁磁状态。根据饱和定律作M-H-1曲线,将其线性部分外推至H-1=0可获得饱和磁化强度Ms。掺杂后的MnBi合金在300 K时,还未完全达到饱和,在400 K时,已经趋于饱和,且在掺杂量小于x=0.12时,饱和磁化强度随着掺杂量的增加而增大,在掺杂量大于x=0.12时,饱和磁化强度已经达到饱和,为20.55 emμ/g,且不随掺杂含量的变化而变化。饱和磁化强度与掺杂含量及温度之间的关系如图 4所示。掺杂后的MnBi低温相合金保持了正矫顽力温度系数这一特性,即在居里温度以下,矫顽力随着温度的上升而增大。同时还可发现矫顽力与掺杂含量的变化,矫顽力首先随着掺杂含量的增加而增大,在掺杂含量为x=0.12时,达到最大值,而后随着掺杂含量的增加,矫顽力反而减小,这是因为MnBi合金具有各向异性,在掺杂量在x=0.08和x=0.12之间存在一个最佳掺杂量,使磁晶取向接近于c轴,从而矫顽力达到最大。
|
| 图 3 MnBi1-xCrx在300 K和400 K的M-H曲线 Fig. 3 M-H curves for MnBi1-xCrx at 300 K and 400 K |
|
| 图 4 300 K和400 K下矫顽力随掺杂含量的变化 Fig. 4 Variation of coercive force with x content at 300 K and 400 K |
2.3 德拜温度
德拜温度ΘD是反映原子间结合力和原子振动的参量,是材料研究中重要的热力学参量。根据德拜模型近似,MnBi1-xCrx(x=0.04)的德拜温度ΘD与晶体内各原子的温度因子BMn,BBi,BCr满足下列关系:
| $ \begin{array}{l} \;\;\;\;\frac{1}{4}\left[ {2\left( {0.953{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.047{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right] = \frac{{6{h^2}T}}{{k\mathit{\Theta }_{\rm{D}}^2}}\left\{ {\mathit{\Phi }(x) + \frac{x}{4}} \right\}, \end{array} $ | (1) |
式中x=ΘD/T,h为普朗克常量,k为玻尔兹曼常数,T为实验温度,Φ(x)为德拜函数,其定义如下:
| $ \mathit{\Phi }(x) = \frac{1}{x}\int_0^x {\frac{y}{{{{\rm{e}}^y} - 1}}} {\rm{d}}y。$ | (2) |
令
| $ \begin{array}{l} \;\;G = \frac{{kT}}{{24{h^2}}}\left[ {2\left( {0.953{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.047{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right], \\ \end{array} $ | (3) |
则方程(1)可以简化为
| $ \mathit{\Phi }\left( x \right) + 4/x = G{x^2}。$ | (4) |
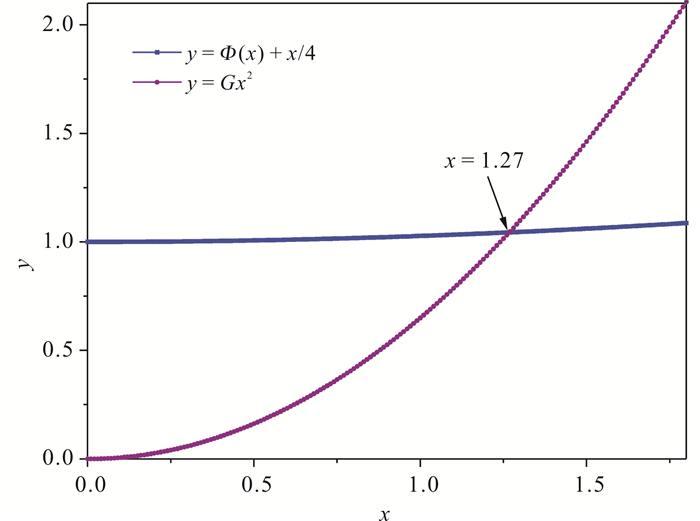
将精修得到的各原子的温度因子BMn,BBi,BCr,如表 2所示,代入(3)式中,可以得到G=0.65。将G值代入方程(4),画出y1=Φ(x)+4/x和y2=Gx2两条曲线(图 5)。求出两条曲线的交点为x=1.27,即当x=1.27时,方程(4)成立。由x=ΘD/T,可以得到合金MnBi1-xCrx(x=0.04)的德拜温度ΘD=378.46 K。
| 掺杂含量 Doping content x |
原子 Atoms* |
占位 Sit occupation |
x | y | z | 占有率 Occupancy rates |
晶胞体积 Lattice volume V(Å3) |
温度因子 Temperature factor Beq(Å2) |
| 0.04 | Mn | 2c | 0 | 0 | 0 | 1 | 0.217 8(2) | |
| M | 2a | 1/3 | 2/3 | 1/4 | (0.923 Bi+0.077 Cr) | 97.281(4) | 0.192 6(3) | |
| 0.08 | Mn | 2c | 0 | 0 | 0 | 1 | 0.258 3(7) | |
| M | 2a | 1/3 | 2/3 | 1/4 | (0.912 Bi+0.088 Cr) | 97.275(2) | 0.195 5(1) | |
| 0.12 | Mn | 2c | 0 | 0 | 0 | 1 | 0.247 1(4) | |
| M | 2a | 1/3 | 2/3 | 1/4 | (0.873 Bi+0.127 Cr) | 97.268(3) | 0.221 7(1) | |
| 0.16 | Mn | 2c | 0 | 0 | 0 | 1 | 0.238 7(5) | |
| M | 2a | 1/3 | 2/3 | 1/4 | (0.086 8 Bi+0.132 Cr) | 97.261(3) | 0.231 7(2) | |
| Note:*M=Bi, Cr | ||||||||
|
| 图 5 MnBi1-xCrx(x=0.04)的德拜温度拟合曲线 Fig. 5 Debye temperature fitting curve of alloy MnBi1-xCrx(x=0.04) |
同理,利用德拜温度近似模型,可以计算样品MnBi1-xCrx(x=0.08)的德拜温度ΘD,其中德拜温度ΘD与晶体内各原子的温度因子BMn,BBi,BCr满足以下关系:
| $ \begin{array}{l} \;\;\;\;\frac{1}{4}\left[ {2\left( {0.912{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.088{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right] = \frac{{6{h^2}T}}{{k\mathit{\Theta }_{\rm{D}}^2}}\left\{ {\mathit{\Phi }(x) + \frac{x}{4}} \right\}, \end{array} $ | (5) |
| $ \begin{array}{l} \;\;\;\;G = \frac{{kT}}{{24{h^2}}}\left[ {2\left( {0.912{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.088{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right]。\end{array} $ | (6) |
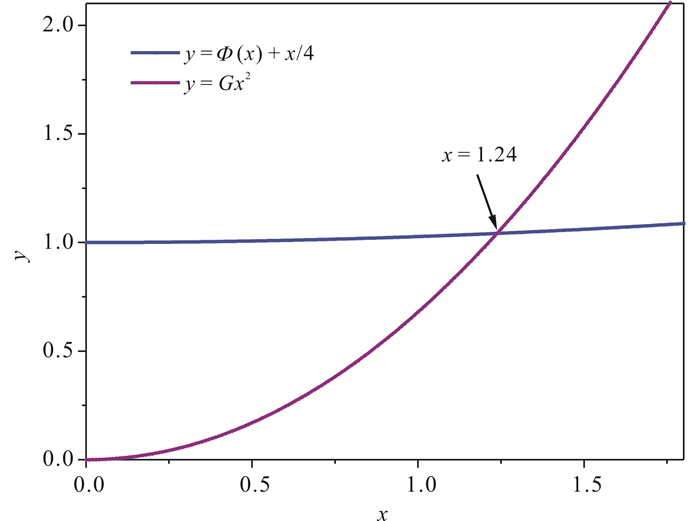
把MnBi1-xCrx(x=0.08)样品Rietveld精修得到的各原子的温度因子BMn,BBi,BCr(表 2)代入(6)中可以得到G=0.68,再把G值代入(4),画出y1=Φ(x)+x/4和y2=Gx2两条曲线(图 6)。求出两条曲线的交点x=1.24, 即当x=1.24时,式(4)成立。x=ΘD/T,可以得到合金MnBi1-xCrx(x=0.08)的德拜温度ΘD=369.52 K。
|
| 图 6 MnBi1-xCrx(x = 0.08)的德拜温度拟合曲线 Fig. 6 Debye temperature fitting curve of alloy MnBi1-xCrx(x=0.08) |
样品MnBi1-xCrx(x=0.12)的德拜温度ΘD与晶体内各原子的温度因子BMn,BBi,BCr满足以下关系:
| $ \begin{array}{l} \;\;\;\;\frac{1}{4}\left[ {2\left( {0.873{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.127{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right] = \frac{{6{h^2}T}}{{k\mathit{\Theta }_{\rm{D}}^2}}\left\{ {\mathit{\Phi }(x) + \frac{x}{4}} \right\}, \end{array} $ | (7) |
| $ \begin{array}{l} \;\;\;\;\;G = \frac{{kT}}{{24{h^2}}}\left[ {2\left( {0.873{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.127{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right]。\end{array} $ | (8) |
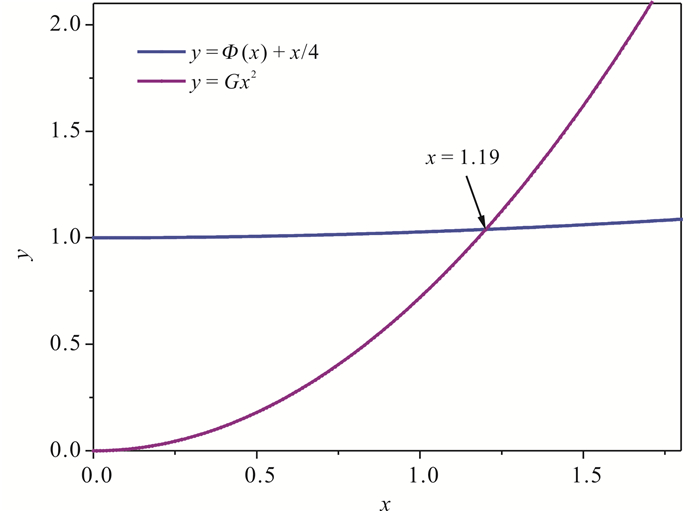
把MnBi1-xCrx(x=0.12)样品Rietveld精修得到的各原子的温度因子BMn,BBi,BCr(表 2)代入(8)中可以得到G=0.72,再把G值代入(4),画出y1=Φ(x)+x/4和y2=Gx2两条曲线(图 7)。求出两条曲线的交点x=1.19,即当x=1.19时,式(4)成立。由x=ΘD/T,可以得到合金MnBi1-xCrx(x=0.12)的德拜温度ΘD=354.62 K。
|
| 图 7 MnBi1-xCrx(x=0.12)的德拜温度拟合曲线 Fig. 7 Debye temperature fitting curve of alloy MnBi1-xCrx(x=0.12) |
样品MnBi1-xCrx(x=0.16)的德拜温度ΘD与晶体内各原子的温度因子BMn,BBi,BCr满足以下关系:
| $ \begin{array}{l} \;\;\;\;\frac{1}{4}\left[ {2\left( {0.868{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.132{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right] = \frac{{6{h^2}T}}{{k\mathit{\Theta }_{\rm{D}}^2}}\left\{ {\mathit{\Phi }(x) + \frac{x}{4}} \right\}, \end{array} $ | (9) |
| $ \begin{array}{l} \;\;\;\;G = \frac{{kT}}{{24{h^2}}}\left[ {2\left( {0.868{m_{{\rm{Bi}}}}{B_{{\rm{Bi}}}} + 0.132{m_{{\rm{Cr}}}}{B_{{\rm{Cr}}}}} \right) + } \right.\\ \left. {2{m_{{\rm{Mn}}}}{B_{{\rm{Mn}}}}} \right]。\end{array} $ | (10) |
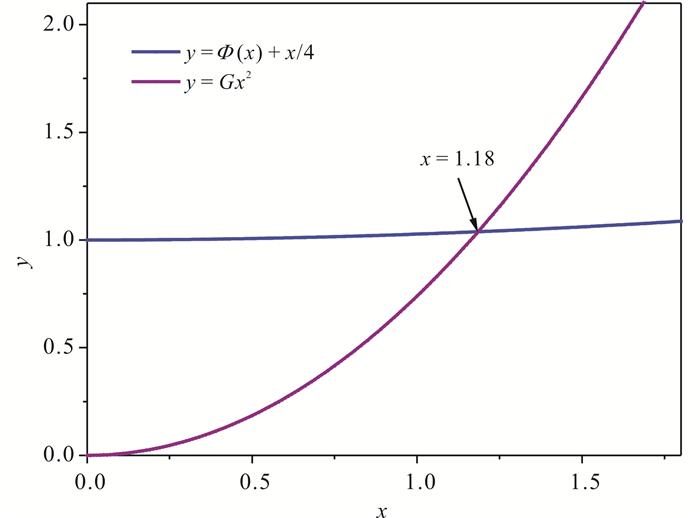
把MnBi1-xCrx(x=0.16)样品Rietveld精修得到的各原子的温度因子BMn,BBi,BCr(表 2)代入(10)中可以得到G=0.74,再把G值代入(4),画出y1=Φ(x)+x/4和y2=Gx2两条曲线(图 8)。求出两条曲线的交点x=1.18,即当x=1.18时,式(4)成立。由x=ΘD/T,可以得到合金MnBi1-xCrx(x=0.16)的德拜温度ΘD=351.64 K。
|
| 图 8 MnBi1-xCrx(x=0.16)的德拜温度拟合曲线 Fig. 8 Debye temperature fitting curve of alloy MnBi1-xCrx(x=0.16) |
3 结论
通过结构精修确定,MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)系列合金中LTP-MnBi相含量都在73%以上。在MnBi1-xCrx中,随着掺杂含量的增加,LTP-MnBi合金的晶胞体积减小。M(M=Bi,Cr)原子之间的原子间距dM-M随着掺杂量增大而增大。M原子与Mn原子的间距dM-Mn随着掺杂量增大而减小。
合金在300 K和400 K温度下均为铁磁状态。掺杂后的MnBi合金在300 K时,还未完全达到饱和,在400 K时,已经趋于饱和,且在掺杂量小于x=0.12时,饱和磁化强度随着掺杂量的增加而增大,在掺杂量大于x=0.12时,饱和磁化强度已经达到饱和,为20.55 emμ/g,且不随掺杂含量的变化而变化。
MnBi1-xCrx(x=0.04, 0.08, 0.12, 0.16)的德拜温度分别为378.46 K,369.52 K,354.62 K和351.64 K。
| [1] |
刘永生.磁场诱导MnBi体系的磁各向异性与自旋重取向相变研究[D].上海: 上海大学, 2005.
|
| [2] |
张素银, 刘泽民, 邵诚, 等. 稀土元素Gd对MnBi合金的微结构与磁性能的影响[J]. 功能材料, 2017, 48(1): 1221-1224. |
| [3] |
方瑞宜, 戴道生, 孙允希, 等. 掺Nd的MnBi薄膜的磁性和磁光特性[J]. 物理学报, 1991, 40(5): 833-843. DOI:10.3321/j.issn:1000-3290.1991.05.023 |
| [4] |
KISHIMOTO M, WAKAI K. Temperature dependence of coercivity of MnBi particles[J]. Japanese Journal of Applied Physics, 1975, 14(6): 893-894. DOI:10.1143/JJAP.14.893 |
| [5] |
SAHA S, OBERMYER R T, ZANDE B J, et al. Magnetic properties of the low-temperature phase of MnBi[J]. Journal of Applied Physics, 2002, 91(10): 8525-8527. DOI:10.1063/1.1450829 |
| [6] |
蒋欢畅.MnBiM(M=Ti, Zr, Ga和Gd)永磁体微结构及其磁性能的研究[D].杭州: 中国计量学院, 2014.
|
| [7] |
ZARKEVICH N A, WANG L L, JOHNSON D D. Anomalous magneto-structural behavior of MnBi explained:A path towards an improved permanent magnet[J]. APL Materials, 2014, 2(3): 260-264. |
| [8] |
ROBERTS B W. Neutron diffraction study of the structures and magnetic properties of manganese bismuthide[J]. Physical Review, 1956, 104(3): 607-616. DOI:10.1103/PhysRev.104.607 |
| [9] |
PIRICH R G, BUSCH G, POIT W, et al. The Bi-MnBi eutectic region of the Bi-Mn phase diagram[J]. American Society for Metals and the Metallurgical Society of Aime, 1980, 11A: 193-194. |
| [10] |
KANG K, LEWIS L H, MOODENBAUGH A R. Alignment and analyses of MnBi/Bi nanostructures[J]. Applied Physics Letters, 2005, 87(6): 62505. DOI:10.1063/1.2008368 |



