车载自组织网(Vehicular ad hoc network,VANET)由若干无线节点和基站组成,不需要固定的基础设施,具有灵活、方便快捷、自学习的特点,极大地弥补了固定网络的不足。在实现通信的过程中,需要路由对网络资源进行分组转发,传统法的路由协议,如AODV[1-2]、DSR[3-4]、GPSR[5]已经无法满足复杂多变的车辆通信。此类问题引起了众多学者关注,并为此加以改进。黄保华等[6]为了提高车载自组织网通信链路的稳定性,提出一种AODV with GASA-FNN (GF-AODV)改进路由算法,有效地降低了平均延迟、能量消耗以及丢包概率。李璞等[7]针对DSR协议修复延迟、频繁泛洪问题,提出一种基于DSR协议的局部路由修复算法,提高了通信的可靠性,有效地减少了网络延迟造成的影响。龚凯等[8]针对车辆通信质量问题,提出一种粒子群算法的GPSR协议优化算法(P-GPSR),对节点的各个参数进行综合优化,实验表明,该改进方案有效提高了路由效率,减少丢包率。虽然上述改进方案在传输延迟、路由维护负荷、链路稳定性等方面有所改善,但是还存在一些不足,仅仅考虑链路稳定而没有实时更新路由信息,特别是在选择下一跳节方面,缺乏适合的调节机制来选择网络拓扑。
目前,在解决VANET问题中,智能优化算法比传统方法更受欢迎。而萤火虫算法(FA)具有简单实现、鲁棒性等特点,已经成功应用于函数优化[9]、神经网络[10]等多个领域。本研究根据VANET的路由特点,将通信服务质量(Quality of service, QoS)的多播路由问题描述为网络寿命最大化或者延迟成本最小化约束问题,利用离散萤火虫算法求解VANET中Steiner minimum tree (SMT)问题,即选择数据包传输的最佳节点。实验表明,与其他算法(Dijkstra最短路径算法、粒子群优化算法)相比,该方案有效解决了VANET通信链路容易断裂问题,降低了网络延迟,并实现实时更新路由信息的功能。
1 VANET的QoS模型VANET通常描述为无向带权图G=(V, E),V是节点集合,E是路径集合。针对VANET中节点运动方向灵活多变、节点间链路稳定性较差、计算成本较大的问题,将VANET中选择通信节点问题转化为选择最短路径的问题,其思想是利用欧式距离进行计算节点之间的距离,把QoS参数作为路径时延度量。即,将QoS问题转化为延迟成本最小化约束优化问题,路径时延包括路径传输时延以及处理时延,路径时延计算公式[11]如下所示。
| $ \begin{array}{l} \;\;\;\;T(path(a, b)) = \sum\limits_{c \in {\rm{path }}(a, b)}^n {T(e) + } \\ \sum\limits_{v \in {\rm{ puth }}a, b}^n T (v), \end{array} $ | (1) |
| $ d(a, b) = \sqrt {{{\left( {{x_a} - {x_b}} \right)}^2} + {{\left( {{y_a} - {y_b}} \right)}^2}} , $ | (2) |
其中,e表示两节点之间的路径,T(e)表示传输时延,v表示节点,T(v)表示处理时延,V集合中任意a、b节点,用path(a, b)表示两点之间路径,T(path(a, b))表示路径时延,d(a, b)表示节点a、b间距离。
在VANET中,数据从源节点传输到目的节点是采用多跳模式,其目的是寻找到时延最小的路径,即目标函数的计算公式为
| $ f{(x)_{\min }} = T(\mathit{path}(a, b))。$ | (3) |
萤火虫算法是根据萤火虫通过发光来传达信息的自然现象而提出的一种群智能优化算法,亮度越强表明其吸引力越大,向其靠拢的可能性就越大。VANET中的SMT问题实际上是离散二进制问题,因此将利用离散型萤火虫(DFA)算法求解此问题。
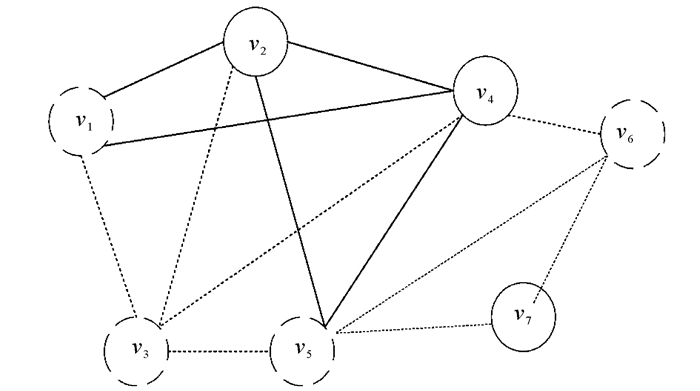
2.1 解的构造在VANET中,除了源节点及目的节点之外,其他都是候选节点。所有节点按照顺序进行编号,候选节点被编码为二进制字符串,取值0或者1,0表示该节点未被选择,1表示该节点被选择。假设v1~v7和13条边构成一个VANET,v1、v5分别是源节点和目的节点,其他节点是候选节点,SMT问题可以描述为在候选节点中选择若干个节点使得通信成本是最小的,DFA算法就是用来搜索最佳候选点组成最短通信路径,一个可行解表示一个候选节点子集,则1010可以表示如图 1,节点v2、v4被选择,节点v3、v6、v7未被选择。DFA算法用来搜索候选节点,不必考虑源节点和目的节点,其他根据概率进行选择若干个,但是选择的节点需要尽可能地减少网络通信成本,由此寻找到满意的解。如果节点链路断开,说明该解是非可行解。其解的结构可以表示成:
| $ {x_i} = \left( {{x_{i1}}, {x_{i2}}, {x_{i3}}, \cdots , {x_{in}}} \right), $ |
|
| 图 1 解的解码子图 Fig. 1 Decoded subgraph of solution |
其中,i=1, 2, 3, …, m;m是萤火虫种群大小;n是节点数。
2.2 萤火虫个体间的距离计算VANET中SMT问题是离散组合优化问题,解向量变量中只有0或者1,则采用计算比较简单的汉明距离公式进行计算萤火虫个体间的距离[12],即两个解之间的距离。设个体i, j位置分别为xi, xj, 其距离记为
| $ h{m_ - }{d_{ij}} = H{m_ - }distance\left( {{x_i}, {x_j}} \right)。$ | (4) |
在VANET问题中,采用的是离散型萤火虫优化算法作为寻找SMT问题中最优节点的搜索策略,即利用计算公式(1)得到路径时延,根据公式(3)可得到目标函数值,f越小,说明该节点是下一跳节点的机会就越大;反之,f越大,说明该节点高延时,距离较远,被选择的机会就越小。DFA算法在选择下一跳节点时并不是按照传统方式选择离目标节点最近邻居节点,而是根据网络路径时延的高低,动态地选择能够获得较好的状态节点传输数据。而这个过程就是通过DFA算法作为搜索策略实现的。
2.4 DFA算法求解SMT问题过程综上,结合DFA算法,求解VANET中SMT问题的步骤如下:
Step 1 初始化各个参数;
Step 2 根据公式(1)计算路径时延适应度值,并根据式(1)、式(5)将其转化为萤火虫的荧光素值
| $ {l_i}(t) = (1 - \rho ){l_i}(t - 1) + \gamma f\left( {{x_i}(t)} \right)。$ | (5) |
在算法迭代过程中,经过萤火虫个体位置更新变换后,可能会出现越界情况,为保持种群的规模和多样性,当开始下一轮迭代后,在利用式(5)更新荧光素值之前,对不满足的解进行重新赋值,保证每次都可以找到可行解,提高搜索速度;
Step 3 使用式(4)计算汉明距离,在其动态决策域半径
Step 4 计算萤火虫个体i向其Ni(t)内的个体j(j∈Ni(t))靠拢的可能性pij(t)
| $ {p_{ij}}(t) = \frac{{{l_j}(t) - {l_i}(t)}}{{\sum\limits_{k \subset {N_i}(t)} {{l_k}} (t) - {l_i}(t)}}; $ | (6) |
Step 5 随机生成0~1之间的变量r,且r(k)∈{r1, r2, …, rk, …,rn},萤火虫位置按照一定的概率,即根据r(k)来选择位置更新;在更新过程中,解的每一维按照一定的概率进行变动,使用式(7)实现位置更新:
| $ \begin{array}{l} {x_{i, k}}(t + 1) = \\ \left\{ {\begin{array}{*{20}{l}} {{x_{ik}}(t), }&{{\rm{if }}\;r(k) \le {p_1}}\\ {{x_{jk}}(t), }&{{\rm{if }}\;{p_1} < r(k) \le {p_2};}\\ {\mathit{round}(rand)}&{{\rm{if }}\;r(k) > {p_2}} \end{array}} \right. \end{array} $ | (7) |
Step 6 利用式(8)更新rdi
| $ \begin{array}{l} \;\;\;r_d^i(t + 1) = \min \left\{ {r, \max \left\{ {0, r_d^i(t) + } \right.} \right.\\ \left. {\left. {\beta \left( {{n_t} - \left| {{N_i}(t)} \right|} \right)} \right\}} \right\}; \end{array} $ | (8) |
Step 7 重复Step 2~Step 6,直到满足终止条件(达到最大迭代次数),就停止迭代。
在DFA中,ρ表示荧光素挥发因子,γ表示荧光素更新率,β表示动态决策域更新率,nt表示Ni内包含的萤火虫数量的阈值,s表示移动步长,rs表示感知半径,t是当前迭代次数。
3 实验及结果分析 3.1 实验环境以及参数设置实验环境是MATLAB 2015Ra,Inter(R) Xeon(R) CPU E5-1620 v3 @3.5 GHz,win8操作系统。DFA算法实验参数参见文献[12],ρ=0.4,γ=0.6,β=0.08,nt=5,s=0.03,初始荧光素值l0=5,p1=0.15,p2=0.85,m=100,初始动态决策域半径rdi(0)=rs=6。设置最大迭代次数iter_max=500,算法运行30次。
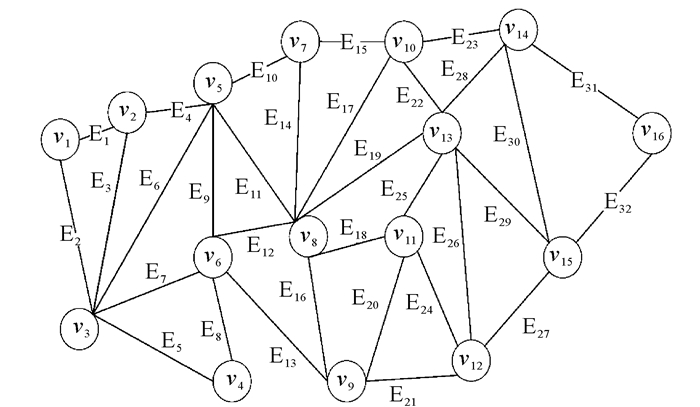
3.2 测试实例如图 2所示,以16个节点组成的VANET为例[13]。其无向带权图G含有32条边,Ad Hoc节点随机放置在400 m×500 m区域中。为了验证算法的性能,在相同的VANET下,使用不同的测试实例将DFA算法与Dijkstra最短路径算法[14]、粒子群优化算法[8]进行对比。
|
| 图 2 测试实例VANET图 Fig. 2 The VANET diagram of test cases |
3.3 仿真结果
实验仿真结果如表 1所示,Best表示在Dijkstra最短路径算法下找到的最优值,当DFA算法找到的最优值与Best的差值的绝对值小于或等于求解精度(10-5),则记录寻优成功一次。
| 实例 Sample |
源节点 Source node |
目的节点 Destiny node |
节点序列 Node list |
最优路径 Optimal path |
最优值 Best |
寻优成功率 SR(%) |
| 1 | v2 | v15 | v2, v5, v8, v13, v15 | E4-E11-E19-E29 | 843.98 | 100 |
| 2 | v2 | v10, v15 | v2, v5, v7, v10, v13, v15 | E4-E10-E15-E22-E29 | 887.52 | 100 |
| 3 | v2 | v4, v9, v10, v15 | v2, v3, v6, v4, v8, v10, v9, v12, v15 | E3-E7-E8-E12-E16-E17-E21-E27 | 1 273.53 | 100 |
| 4 | v2 | v3, v4, v9, v10, v13, v15 | v2, v5, v6, v4, v8, v10, v9, v13, v15 | E4-E9-E8-E12-E16-E17-E22-E29 | 1 303.45 | 100 |
由表 1中SR可知,利用DFA算法都可以成功寻找4个实例的最优路径,说明用该算法解决该VANET中SMT问题是有效的。
为了对比DFA算法与Dijkstra最短路径算法[14]、粒子群优化算法[8]的优劣,本实验是以算法平均运行时间(Average running time, ART)、端到端平均时延时间(Average delay time, ADT)为度量。
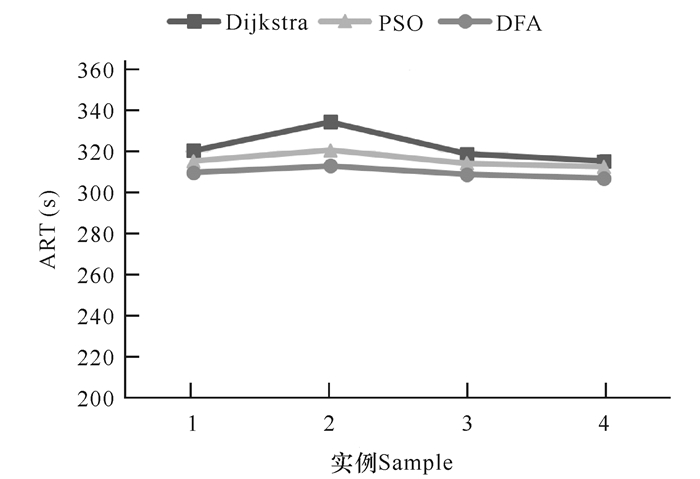
3.4 算法平均运行时间算法平均运行时间(ART)指算法达到最佳值的平均运行时间,4个实例的ART如图 3所示。
|
| 图 3 ART变化图 Fig. 3 Chart of ART change |
据图 3可知,当源节点和目的节点数量增多时,3种算法的变化趋势基本一致,ART先增后减,但是4个实例中DFA算法ART值优于其他两种算法;对于DFA算法来说,ART值变化不大,说明该算法在解决VANET中的SMT问题中是可行的。
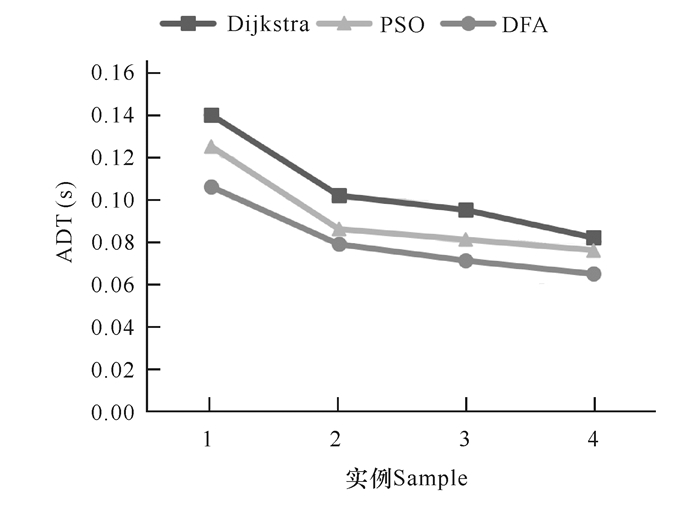
3.5 端到端平均时延时间端到端平均时延时间(ADT)是指数据从源节点传输到目的节点的时间平均值。4个实例运行30次时延时间的平均值如图 4所示。
|
| 图 4 ADT变化图 Fig. 4 Chart of ADT change |
由图 4可知,随着VNAET中节点数的增加,3种算法的ADT均呈现下降趋势。原因是节点数增加则可以被选择的节点数也增加,数据就能更快速地传输到目的节点。另外,使用DFA算法根据路径时延转化为萤火虫荧光素值来选择下一跳节点,减少了数据传输过程的时延,进一步降低了数据包的端到端时延时间,也说明了在网络拓扑结构比较稳定的通信链路中,可以实时应用多播路由算法。
综上,用DFA算法求解VANET问题是可行有效的,且比Dijkstra最短路径算法和粒子群优化算法性能更佳,原因主要有:
第一,将VANET中多播路由问题简单化描述成为连续优化问题,其最终目标是最小化通信成本。实际上是解决QoS中多播路由中的SMT问题。
第二,基于经典萤火虫算法,提出了离散型萤火虫算法,并用二进制形式表示,将其作为寻找VANET中最优节点的搜索策略。
第三,在求解萤火虫算法个体之间距离时采用的是汉明距离公式求解,可直接对个体间二进制形式的解求解不同字符的个数,没有使用传统的欧氏距离公式,加快了算法的求解速度。
4 结论在QoS约束VANET中,将VANET问题转化为图形问题,并将其转化为搜索SMT最短路径问题。由于最短路径的选择,实际上是稳固了通信链路,不经常变化的网络使得路由信息容易实时更新。用DFA算法搜索最短路径,即候选节点的选择,能够较大程度提升通信链路的稳定性,减少通信链路的时延。
在以后的工作中,将对VANET进行更深入地研究,尝试将其他智能算法作为搜索策略。
| [1] |
DAS S R, BELDING-ROYER E M, PERKINS C E.Ad-hoc on-demand distance vector (AODV) routing[EB/OL].[2019-02-04].http://www.ietf.org/rfc/rfc3561.
|
| [2] |
VERMA V K, SINGH S, PATHAK N P. Analysis of scalability for AODV routing protocol in wireless sensor networks[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(2): 748-750. DOI:10.1016/j.ijleo.2013.07.041 |
| [3] |
CHENG Y, ÇETINKAYA E K, STERBENZ J P G.Dynamic source routing (DSR) protocol implementation in ns-3[C]//SIMUTOOLS'12 Proceedings of the 5th International ICST Conference on Simulation Tools and Techniques.Brussels, Belgium: International ICST Conference on Simulation TOOLS and Techniques, 2012: 367-374.
|
| [4] |
JOHNSON D B, MALTZ D A.Dynamic source routing in Ad Hoc wireless networks[M]//IMIELINSKI T, KORTH H F (eds).Mobile computing.The kluwer international series in engineering and computer science, Vol.353.Boston: Springer, 1996: 153-181.
|
| [5] |
KARP B, KUNG H T.GPSR: Greedy perimeter stateless routing for wireless networks[C].MobiCom'00 Proceedings of the 6th Annual International Conference on Mobile Computing and Networking.Boston, Massachusetts, USA, 2000: 243-254.
|
| [6] |
黄保华, 莫家威, 吕琦. 基于模糊神经网络的稳定AODV协议改进方案[J]. 计算机工程与科学, 2018, 40(11): 1974-1982. DOI:10.3969/j.issn.1007-130X.2018.11.009 |
| [7] |
李璞, 彭鹏菲. 基于DSR协议的局部路由修复算法[J]. 指挥控制与仿真, 2018, 40(1): 72-74. DOI:10.3969/j.issn.1673-3819.2018.01.014 |
| [8] |
龚凯, 陈志, 岳文静. 基于粒子群算法的车载自组网GPSR协议优化[J]. 计算机技术与发展, 2018, 28(11): 184-188, 193. |
| [9] |
郗君甫. 基于动态自适应萤火虫优化算法[J]. 邢台职业技术学院学报, 2017, 34(5): 78-82. DOI:10.3969/j.issn.1008-6129.2017.05.021 |
| [10] |
张明, 张树群, 雷兆宜. 改进的萤火虫算法在神经网络中的应用[J]. 计算机工程与应用, 2017, 53(5): 159-163. |
| [11] |
周杰英, 彭石, 刘映淋, 等. 车载自组网中一种自适应粒子群算法的研究[J]. 现代计算机:专业版, 2017(11): 26-30. |
| [12] |
倪志伟, 肖宏旺, 伍章俊, 等. 基于改进离散型萤火虫群优化算法和分形维数的属性选择方法[J]. 模式识别与人工智能, 2013, 26(12): 1169-1178. DOI:10.3969/j.issn.1003-6059.2013.12.011 |
| [13] |
ZHANG X, ZHANG X, GU C. A micro-artificial bee colony based multicast routing in vehicular ad hoc networks[J]. Ad Hoc Networks, 2017, 58(2): 213-221. |
| [14] |
ZHANG B, LIU Y, CHEN C.An efficient delay-constrained multicast routing algorithm[C].International Conference on Communication Technology Proceedings.Beijing, China: IEEE, 2002.
|


