2. 百色学院数学与统计学院, 广西百色 533000
2. School of Mathematics and Statistics, Baise University, Baise, Guangxi, 533000, China
在振动系统、潮流方程等科学与工程计算领域存在许多大规模优化问题[1, 2],而这些优化问题往往能够转化为非线性方程组问题。因此,研究求解大规模非线性方程组的高效数值算法具有重要的理论价值与实际意义。
本文主要考虑以下非线性方程组问题:
| $ F\left( x \right) = 0, x \in {R^n}, $ | (1) |
其中F:Rn→Rn是连续可微非线性函数。令
| $ \min f\left( x \right), x \in {R^n}。$ |
近年来,求解上述优化问题的常见算法有牛顿法、信赖域法、拟牛顿法、Levenberg-Marquardt算法及其各种变形[3-8]。在选择合理初始点的前提下,上述算法对于小规模优化问题具有快速收敛和数值效果良好等特点,但在迭代过程中,需要计算和存储相关矩阵信息,给求解大规模优化问题带来一定的局限性。为建立求解大规模优化问题的高效算法体系,研究者提出具有算法简单、计算和存储量低等优点的共轭梯度法[9-11]。
经典共轭梯度法的一般迭代公式为
| $ {x_{k + 1}} = {x_k} + {a_k}{d_k}, k = 0, 1, 2, \ldots , $ |
其中αk为由某种线搜索所决定的步长。搜索方向dk为
| $ {d_k} = \left\{ \begin{array}{l} \;\;\;\;\; - {F_k}, \;\;\;\;\;\;\;k = 0\\ - {F_k} + {\beta _k}{d_{k - 1}}, k \ge 1 \end{array} \right., $ |
其中, βk为共轭参数,Fk为F(xk)的简写。
本文基于Abubakar等[12]提出的修正FR搜索方向,借鉴Yuan等[13]的凸组合思想,构造凸组合系数如下:
| $ {N_k} = \frac{{{{\left\| {{y_{k - 1}}} \right\|}^2}}}{{y_{k - 1}^t\omega _{k - 1}^ * }}, $ |
其中:
同时,采用Andrei[14]的加速线搜索技术,提出一个求解大规模非线性方程组问题的加速FR型共轭梯度算法。
1 算法描述与性质本节主要讨论搜索方向的构建并介绍线搜索技术,同时提出凸组合修正共轭梯度算法。
首先,Abubakar等[12]在2019年提出一种修正FR共轭梯度法,其搜索方向为
| $ \begin{array}{l} {d_k} = \\ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {F_k}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0\\ - {F_k} + \frac{{{{\left\| {{F_k}} \right\|}^2}{\omega _{k - 1}} - F_k^{\rm{T}}{\omega _{k - 1}}{F_k}}}{{\max \left\{ {\mu \left\| {{\omega _{k - 1}}} \right\|\left\| {{F_b}} \right\|, {{\left\| {{F_{b - 1}}} \right\|}^2}} \right\}}}, k \ge 1 \end{array} \right., \end{array} $ |
其中, ωk-1 =xk -xk-1, μ >0。该搜索方向具备充分下降性和信赖域特征,能有效求解大规模无约束优化问题。基于Yuan等[13]的凸组合思想,本文构建一个新型的凸组合搜索方向:
| $ {d_k} = \left\{ \begin{array}{l} - {F_k}, k = 0\\ - {N_k}{F_k} + \left( {1 - {N_k}} \right)\left( {{{\left\| {{F_k}} \right\|}^2}{\omega _{k - 1}} - F_k^{\rm{T}}{\omega _{k - 1}}{F_k}} \right)/\\ \;\;\;\max \left\{ {2\mu \left\| {{\omega _{k1}}} \right\|\left\| {{F_k}} \right\|, {{\left\| {{F_{k1}}} \right\|}^2}} \right\}, k \ge 1 \end{array} \right., $ | (2) |
其中,Nk满足如下性质:
其次,本文通过下述方法计算步长αk=rmk,使得mk满足下式的最小非负整数,即
| $ f({x_k} + {r^m}{d_k}) - f({x_k}){\rm{ }} \le \sigma {({r^m})^2}F_k^{\rm{T}}{d_k}, $ | (3) |
其中,σ∈(0, 1), r∈(0, 1)。Andrei[14]研究表明,合理地应用加速线搜索,将有效提高算法的计算效率。于是借鉴于Andrei[14]的加速线搜索技术思想,对步长αk做出修正,即
| $ \tilde \alpha = {\gamma _k}{\alpha _k}, $ |
其中
最后,建立求解非线性方程组问题(1)的凸组合加速FR型共轭梯度算法(MMFR)。
步骤1:给定初始点x0∈Rn,参数ε, σ, r, β, μ∈(0, 1),令k:=0;
步骤2:若‖ Fk‖≤ε,则算法停止;
步骤3:通过式(2)计算搜索方向dk;
步骤4:若‖F(xk+dk)‖≤β‖Fk‖,则令步长αk=1,转步骤6,否则转步骤5;
步骤5:通过式(3)决定步长αk;
步骤6:计算θk和ã ,若θk>0,则令αk=ã,否则保持步长αk不变;
步骤7:(更新步)更新新的迭代点xk+1=xk+αkdk,令k:=k+1,转步骤2。
为后续证明算法的全局收敛性质,下面分析搜索方向dk的两个重要性质:充分下降性和信赖域特性。
引理1 算法MMFR产生的序列 dk 和 Fk 满足以下性质:
| $ F_k^{\rm{T}}{d_k} \le - {N_k}{\left\| {{F_k}} \right\|^2}, $ | (4) |
及
| $ \left\| {{d_k}} \right\|{\rm{ }} \le {\tau _k}\left\| {{F_k}} \right\|{\rm{ }}, $ | (5) |
其中,
证明:当k=0时,F0Td0=-‖F0‖2, ‖d0‖=‖F0 ‖,显然式(4)(5)成立。当k≥1时,由式(2)左乘FkT得
| $ \begin{array}{l} F_k^{\rm{T}}{d_k} = - {N_k}{\left\| {{F_k}} \right\|^2} + \\ \left( {1 - {N_k}} \right)\frac{{{{\left\| {{F_k}} \right\|}^2}\omega _{k - 1}^{\rm{T}}{F_k} - F_k^{\rm{T}}{\omega _{k - 1}}F_k^{\rm{T}}{F_k}}}{{{\rm{max }}\left\{ {2\mu \left\| {{\omega _{k - 1}}} \right\|{\rm{ }}\left\| {{F_k}} \right\|{\rm{ }}, {\rm{ }}{{\left\| {{F_{k - 1}}} \right\|}^2}} \right\}}} \le \\ - {\rm{ }}{N_k}{\left\| {{F_k}} \right\|^2}。\end{array} $ |
此外,由式(2)和Cauchy-Schwartz不等式可知
| $ \begin{array}{*{20}{l}} {\left\| {{d_k}} \right\| = \left\| { - {N_k}{F_k} + \left( {1 - {N_k}} \right)} \right. \cdot }\\ \begin{array}{l} \left. {\frac{{{{\left\| {{F_k}} \right\|}^2}{\omega _{k - 1}} - F_k^{\rm{T}}{\omega _{k - 1}}{F_k}}}{{\max \left\{ {2\mu \left\| {{\omega _{k - 1}}} \right\|\left\| {{F_k}} \right\|,{{\left\| {{F_{k - 1}}} \right\|}^2}} \right\}}}} \right\| \le \\ {N_k}\left\| {{F_k}} \right\| + \left( {1 - {N_k}} \right). \end{array}\\ {\frac{{{{\left\| {{F_k}} \right\|}^2}\left\| {{\omega _{k - 1}}} \right\| + \left\| {{F_k}} \right\|\left\| {{\omega _{k - 1}}} \right\|\left\| {{F_k}} \right\|}}{{2\mu \left\| {{\omega _{k - 1}}} \right\|\left\| {{F_k}} \right\|}} \le }\\ {\left( {{N_k} + \left( {1 - {N_k}} \right)\frac{1}{\mu }} \right)\left\| {{F_k}} \right\|,} \end{array} $ |
综上所述,式(4)和式(5)成立, 引理1得证。
2 全局收敛性分析为进一步分析算法MMFR的收敛性,本节做如下假设:
假设H
(H1) 函数F(x)在开凸集Ω1⊆Ω= {x|‖F (x) ‖≤‖F (x0)‖是连续可微的;
(H2) 函数F (x)的雅可比矩阵为▽F (x)是有界的且为对称正定矩阵,即存在正常数ξ1≥ξ2>0,使得有‖▽F (x) ‖≤ξ1和ξ2‖p‖2≤pT▽F (x) p≤ξ1‖p‖2, p∈Rn。
引理2 在假设H条件下,序列{ xk}、{αk}、{Fk}和{dk}是由算法MMFR产生的,那么{‖ Fk‖ }为单调递减的收敛序列且
证明:由Brown等[15]的引理3.8可得
f(xk+rmdk)-f(xk)≤σ1(rm)2FkT▽Fkdk,利用假设H2的公式,结合上式得f(xk+rmdk)-f(xk)≤σ(rm)2FkTdk,其中σ=σ1ξ1。因此,线搜索是适定的。
由引理1和式(3)可推出
| $ f({x_k} + {\alpha _k}{d_k}) - f({x_k}){\rm{ }} \le - \sigma \alpha _k^2{N_k}{\left\| {{F_k}} \right\|^2} \le 0, $ | (6) |
这说明函数f(x)沿着下降方向dk是充分下降的。公式(6)结合f(x)的定义可知,对于任意的k,都有‖Fk+1‖≤‖Fk‖。此外,由式(3)和式(4)得出
| $ \begin{array}{l} \mathop {\lim }\limits_{k \to \infty } f\left( {{x_k} + {a_k}{d_k}} \right) - f\left( {{x_0}} \right) = \\ \sum\limits_{k = 0}^\infty {f\left( {{x_k} + {a_k}{d_k}} \right) - f\left( {{x_k}} \right) \le - \sigma \sum\limits_{k = 0}^\infty {{N_k}{{\left\| {{a_k}{F_k}} \right\|}^2}} } 。\end{array} $ |
由假设H1中函数的有界性,再结合上式得
| $ \begin{array}{l} \;\;\;\;\;\;\sigma \sum\limits_{k = 0}^\infty {{N_k}{{\left\| {{a_k}{F_k}} \right\|}^2}} \le \mathop {\lim }\limits_{k \to \infty } f\left( {{x_0}} \right) - f({x_k} + \\ {a_k}{d_k}) < \infty , \end{array} $ |
再结合Nk∈ (0, 1]推得
下面给出算法MMFR的全局收敛性定理。
定理1 在假设H条件下,序列{ xk}、{αk}、{ Fk}和{dk}是由算法MMFR产生的,那么有
证明:由引理2可知,若
| $ f\left( {{x_k} + {{\overline \alpha }_k}{d_k}} \right) - f\left( {{x_k}} \right) > \sigma \overline \alpha _k^2F_k^{\rm{T}}{d_k}。$ | (7) |
假设结论不成立,即存在正整数ξ,对于任意k,那么有
| $ \left\| {\nabla f\left( {{x_k}} \right)} \right\| > \xi 。$ | (8) |
另外,由假设H1可知,集合为有界集合,则序列{xk }是有界的,于是可得序列{dk}也是有界的。不失一般性,设点x*和d*分别为序列{ xk }和{ dk }的聚点。因此,对式(7)取极限得
| $ \nabla f{\left( {{x^ * }} \right)^T}{d^ * } \ge 0。$ |
同理,对式(6)取极限得
| $ \nabla f{\left( {{x^ * }} \right)^{\rm{T}}}{d^ * } \le 0。$ |
上述两不等式可推出▽f(x*)Td*=0,由于‖d*‖≠0 (如果‖d*‖=0,那么由式(4)知‖F(x*)‖=0),故‖▽f(x*)‖=0,这与式(8)矛盾,于是结论成立。
定理1说明序列{ xk }至少是线性收敛的,下面定理给出算法MMFR具有强收敛性质。
定理2 在假设H条件下,若算法MMFR产生的任一子序列{ xk }收敛于聚点x*,则非线性方程组问题(1)的最优解为x*,进一步有序列{ xk }整列收敛于x*。
证明:类似于Yuan[16]中定理3.4的证明方法,易证结论成立,故省略证明过程。
3 数值试验本节通过比较算法MMFR、经典FR、三项FR算法在求解大规模非线性方程组问题上的数值结果,验证算法MMFR的有效性与稳定性。
下面给出经典FR算法和三项FR算法的搜索方向,分别为
| $ {d_k} = \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\; - {F_k}, \;\;\;\;\;\;\;\;\;k = 0\\ - {F_k} + \frac{{{{\left\| {{F_k}} \right\|}^2}}}{{{{\left\| {{F_{k - 1}}} \right\|}^2}}}{d_{k - 1}}, k \ge 1 \end{array} \right., $ | (9) |
| $ \begin{array}{l} \;\;\;\;\;{d_k}{\rm{ = }}\\ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {F_k}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0\\ - {F_k} + \frac{{{{\left\| {{F_k}} \right\|}^2}}}{{{{\left\| {{F_{k - 1}}} \right\|}^2}}}{\omega _{k - 1}}{\rm{ + }}\frac{{F_k^{\rm{T}}{\omega _{k - 1}}}}{{{{\left\| {{F_{k - 1}}} \right\|}^2}}}{F_k}, k \ge 1 \end{array} \right.。\end{array} $ | (10) |
在算法MMFR的步骤2中,分别采用式(9)和式(10)产生搜索方向,其余步骤不变,得到的算法记为FR算法和MFR算法。
参数设置:r=0.5, σ=0.068, μ=0.25, β=0.5。程序运行环境:MATLAB(2014a)软件实现,Windows10 (64 bite),RAM:8 G,CPU 3.60 GHz。
算法终止准则为‖Fk‖≤10-5或Iter>3000,维数为[4500, 12000, 24000, 30000, 45000]。测试问题的函数名称和初始点[17]见表 1,数值试验结果如表 2所示,其中Pro (Problem)为问题序号,Dim (Dimension)为维数,Iter (Iterations)为迭代次数,NF(The number of function)为函数F(x)计算次数,Time为程序运行时间(单位:s)。根据迭代次数、函数计算次数和运行时间可以看出,总体上算法MMFR最好,算法MFR其次,算法FR最差(表 2)。
| 序号 Number |
函数名称 Function name |
初始点 Initial point |
| 1 | Exponential function 2 | |
| 2 | Trigonometric function | |
| 3 | Broyden tridiagonal function | -1, -1, ..., -1 |
| 4 | Trigexp function | 0, 0, ..., 0 |
| 5 | Strictly convex function 1 | |
| 6 | Variable dimensioned function | |
| 7 | Five-diagonal system | -2, -2, ..., -2 |
| 8 | Extended freudentein and roth function | 6, 3, ..., 6, 3 |
| 9 | Discrete boundry value problem | h×(1×h-1), h×(2×h-1), ..., h×(n×h-1), h= 1/(n+1) |
| 10 | Troesch problem | 0.5, 0.5, ..., 0.5 |
| 问题 Pro |
维数 Dim |
MMFR | FR | MFR | ||||||||
| 迭代次数 Iter |
计算次数 NF |
运行时间 Time |
迭代次数 Iter |
计算次数 NF |
运行时间 Time |
迭代次数 Iter |
计算次数 NF |
运行时间 Time |
||||
| 1 | 4 500 | 17 | 193 | 3.47E-02 | 12 | 133 | 2.63E-02 | 17 | 193 | 3.44E-02 | ||
| 12 000 | 12 | 148 | 6.58E-02 | 14 | 179 | 8.55E-02 | 12 | 148 | 6.42E-02 | |||
| 24 000 | 9 | 116 | 9.87E-02 | 13 | 177 | 1.58E-01 | 9 | 116 | 9.70E-02 | |||
| 30 000 | 10 | 134 | 1.37E-01 | 14 | 189 | 2.05E-01 | 10 | 134 | 1.35E-01 | |||
| 45 000 | 9 | 123 | 1.96E-01 | 20 | 286 | 4.61E-01 | 9 | 123 | 1.94E-01 | |||
| 2 | 4 500 | 9 | 21 | 1.26E-02 | 114 | 674 | 3.97E-01 | 8 | 28 | 1.64E-02 | ||
| 12 000 | 8 | 19 | 2.98E-02 | 103 | 608 | 9.24E-01 | 8 | 28 | 4.19E-02 | |||
| 24 000 | 8 | 19 | 5.72E-02 | 99 | 584 | 1.74E+00 | 8 | 28 | 8.04E-02 | |||
| 30 000 | 8 | 19 | 6.85E-02 | 103 | 608 | 2.25E+00 | 8 | 28 | 9.88E-02 | |||
| 45 000 | 8 | 19 | 1.03E-01 | 104 | 614 | 3.43E+00 | 8 | 28 | 1.48E-01 | |||
| 3 | 4 500 | 32 | 147 | 2.81E-02 | 1 685 | 24 996 | 4.37E+00 | 78 | 382 | 6.84E-02 | ||
| 12 000 | 33 | 152 | 7.23E-02 | 1 732 | 25 644 | 1.12E+01 | 74 | 362 | 1.61E-01 | |||
| 24 000 | 32 | 146 | 1.32E-01 | 1 745 | 25 794 | 2.19E+01 | 71 | 347 | 3.02E-01 | |||
| 30 000 | 33 | 151 | 1.69E-01 | 1 751 | 25 876 | 2.71E+01 | 64 | 312 | 3.38E-01 | |||
| 45 000 | 33 | 151 | 2.64E-01 | 1 753 | 25 893 | 4.21E+01 | 69 | 336 | 5.54E-01 | |||
| 4 | 4 500 | 73 | 433 | 1.77E-01 | 1 116 | 16 252 | 6.46E+00 | 1 743 | 10 459 | 4.30E+00 | ||
| 12 000 | 73 | 433 | 4.58E-01 | 1 117 | 16 266 | 1.66E+01 | 1 743 | 10 459 | 1.10E+01 | |||
| 24 000 | 73 | 433 | 8.98E-01 | 1 117 | 16 266 | 3.28E+01 | 1 743 | 10 459 | 2.14E+01 | |||
| 30 000 | 73 | 433 | 1.11E+00 | 1 117 | 16 266 | 4.09E+01 | 1 743 | 10 459 | 2.65E+01 | |||
| 45 000 | 73 | 433 | 1.68E+00 | 1 118 | 16 280 | 6.15E+01 | 1 743 | 10 459 | 3.93E+01 | |||
| 5 | 4 500 | 25 | 72 | 1.62E-02 | 13 | 25 | 4.86E-03 | 9 | 17 | 3.37E-03 | ||
| 12 000 | 25 | 72 | 4.01E-02 | 13 | 25 | 1.20E-02 | 9 | 17 | 8.30E-03 | |||
| 24 000 | 26 | 75 | 7.70E-02 | 13 | 25 | 2.27E-02 | 9 | 17 | 1.58E-02 | |||
| 30 000 | 26 | 75 | 9.49E-02 | 13 | 25 | 2.81E-02 | 9 | 17 | 1.97E-02 | |||
| 45 000 | 26 | 75 | 1.48E-01 | 13 | 25 | 4.47E-02 | 9 | 17 | 3.07E-02 | |||
| 6 | 4 500 | 2 | 3 | 1.85E-04 | 2 | 3 | 1.91E-04 | 2 | 3 | 1.94E-04 | ||
| 12 000 | 2 | 3 | 3.68E-04 | 2 | 3 | 3.89E-04 | 2 | 3 | 3.69E-04 | |||
| 24 000 | 2 | 3 | 6.24E-04 | 2 | 3 | 6.31E-04 | 2 | 3 | 6.25E-04 | |||
| 30 000 | 2 | 3 | 7.68E-04 | 2 | 3 | 7.68E-04 | 2 | 3 | 7.56E-04 | |||
| 45 000 | 2 | 3 | 2.05E-03 | 2 | 3 | 2.07E-03 | 2 | 3 | 2.07E-03 | |||
| 7 | 4 500 | 357 | 2 472 | 7.49E-01 | 1 398 | 20 345 | 6.05E+00 | 2 320 | 16 232 | 4.86E+00 | ||
| 12 000 | 359 | 2 485 | 1.92E+00 | 1 038 | 14 996 | 1.14E+01 | 304 | 2 058 | 1.55E+00 | |||
| 24 000 | 360 | 2 492 | 3.75E+00 | 1 061 | 15 218 | 2.26E+01 | 2 345 | 16 407 | 2.44E+01 | |||
| 30 000 | 360 | 2 492 | 4.64E+00 | 1 052 | 15 175 | 2.80E+01 | 311 | 2 119 | 3.89E+00 | |||
| 45 000 | 359 | 2 485 | 7.09E+00 | 1 070 | 15 479 | 4.37E+01 | 299 | 2 025 | 5.67E+00 | |||
| 8 | 4 500 | 199 | 1 510 | 3.05E-01 | 93 | 996 | 1.93E-01 | 117 | 798 | 1.56E-01 | ||
| 12 000 | 207 | 1 572 | 7.98E-01 | 96 | 1 017 | 4.91E-01 | 120 | 820 | 4.02E-01 | |||
| 24 000 | 211 | 1 603 | 1.56E+00 | 97 | 1 024 | 9.61E-01 | 124 | 847 | 8.04E-01 | |||
| 30 000 | 214 | 1 627 | 1.96E+00 | 98 | 1 030 | 1.20E+00 | 124 | 847 | 9.95E-01 | |||
| 45 000 | 215 | 1 634 | 3.05E+00 | 98 | 1 030 | 1.85E+00 | 125 | 853 | 1.55E+00 | |||
| 9 | 4 500 | 10 | 36 | 2.64E-02 | 3 000 | 46 931 | 3.39E+01 | 15 | 66 | 4.79E-02 | ||
| 12 000 | 6 | 20 | 3.84E-02 | 3 000 | 46 931 | 8.81E+01 | 11 | 46 | 8.70E-02 | |||
| 24 000 | 4 | 13 | 4.94E-02 | 25 | 221 | 8.14E-01 | 7 | 27 | 1.00E-01 | |||
| 30 000 | 3 | 9 | 4.17E-02 | 5 | 18 | 8.22E-02 | 6 | 22 | 1.01E-01 | |||
| 45 000 | 3 | 9 | 6.24E-02 | 4 | 13 | 8.97E-02 | 4 | 13 | 8.99E-02 | |||
| 10 | 4 500 | 3 | 4 | 2.05E-04 | 3 | 4 | 1.91E-04 | 3 | 4 | 1.97E-04 | ||
| 12 000 | 3 | 4 | 3.82E-04 | 3 | 4 | 3.66E-04 | 3 | 4 | 3.73E-04 | |||
| 24 000 | 3 | 4 | 6.29E-04 | 3 | 4 | 6.27E-04 | 3 | 4 | 6.35E-04 | |||
| 30 000 | 3 | 4 | 7.68E-04 | 3 | 4 | 7.66E-04 | 3 | 4 | 7.71E-04 | |||
| 45 000 | 3 | 4 | 2.06E-03 | 3 | 4 | 2.08E-03 | 3 | 4 | 2.01E-03 | |||
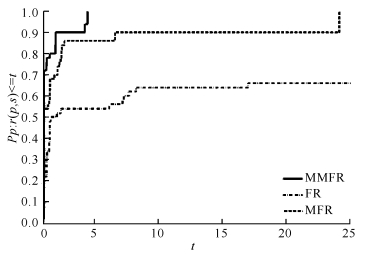
为直观地展示3种算法的性能差异,本节采用性能曲线描绘方法[18]分别描绘出迭代次数性能图、函数计算次数性能图和运行时间性能图(图 1-3)。由图 1-3可知,算法MMFR总体上比算法MFR和算法FR更优,且具有更好的鲁棒性,因此本文提出的算法MMFR是有效的和鲁棒的。

|
| 图 1 迭代次数性能图 Fig. 1 Performance profiles of the number of iterations |
|
| 图 2 函数计算次数性能图 Fig. 2 Performance profiles of the number of computing function |

|
| 图 3 运行时间性能图 Fig. 3 Performance profiles of CPU-Time |
4 结论
本文在修正FR算法的基础上,结合凸组合思想,构造出一个新的修正搜索方向,并利用加速线搜索技术,提出一个加速FR型共轭梯度算法。新的搜索方向不依赖线搜索, 具有充分下降和信赖域特性,还具有良好的理论性质与数值效果。因计算简单,存储量小,十分适合求解大规模非线性方程组问题。同时,也可尝试将新算法进一步推广到信号恢复等实际应用中。
| [1] |
WANG Y J, CACCETTA L, ZHOU G L. Convergence analysis of a block improvement method for polynomial optimization over unit spheres[J]. Numerical Linear Algebra with Applications, 2015, 22(6): 1059-1076. DOI:10.1002/nla.1996 |
| [2] |
WANG C W, WANG Y J. A superlinearly convergent projection method for constrained systems of nonlinear equations[J]. Journal of Global Optimization, 2009, 44(2): 283-296. DOI:10.1007/s10898-008-9324-8 |
| [3] |
YUAN G L, WEI Z X. A trust region algorithm with conjugate gradient technique for optimization problems[J]. Numerical Functional Analysis and Optimization, 2011, 32(2): 212-232. DOI:10.1080/01630563.2010.532273 |
| [4] |
GAO H, ZHANG H B, LI Z B, et al. A nonmonotone inexact Newton method for unconstrained optimization[J]. Optimization Letters, 2017, 11(5): 947-965. DOI:10.1007/s11590-015-0976-2 |
| [5] |
CAO H P. A new Quasi-Newton method based on adjoint broyden updates for symmetric nonlinear equations[J]. Journal of the Korean Mathematical Society, 2016, 53(6): 1371-1389. DOI:10.4134/JKMS.j150542 |
| [6] |
ZHOU Q Y, SUN W Y, ZHANG H C. A new simple model trust-region method with generalized Barzilai-Borwein parameter for large-scale optimization[J]. Science China Mathematics, 2016, 59(11): 2265-2280. DOI:10.1007/s11425-015-0734-2 |
| [7] |
NIRI T D, FAZELI S A S, HEYDARI M. A two-step improved Newton method to solve convex unconstrained optimization problems[J]. Journal of Applied Mathematics and Computing, 2020, 62(1): 37-53. DOI:10.1007/s12190-019-01272-z |
| [8] |
CHEN L, MA Y F. Shamanskii-Like Levenberg-Marquardt method with a new line search for systems of nonlinear equations[J]. Journal of Systems Science and Complexity, 2020, 33(5): 1694-1707. DOI:10.1007/s11424-020-9043-x |
| [9] |
王松华, 吴加其. 新线搜索下修正PRP共轭梯度法的全局收敛性及其数值结果[J]. 广西科学, 2018, 25(6): 728-733. |
| [10] |
DJORDJEVIĆ S S. New hybrid conjugate gradient me-thod as a convex combination of Ls and Fr methods[J]. Acta Mathematica Scientia:English Series, 2019, 39(1): 214-228. DOI:10.1007/s10473-019-0117-6 |
| [11] |
DAI Y H, KOU C X. A Barzilai-Borwein conjugate gradient method[J]. Science China Mathematics, 2016, 59(8): 1511-1524. DOI:10.1007/s11425-016-0279-2 |
| [12] |
ABUBAKAR A B, KUMAM P, MOHAMMAD H, et al. A modified Fletcher-Reeves conjugate gradient method for monotone nonlinear equations with some applications[J]. Mathematics, 2019, 7(8): 745. DOI:10.3390/math7080745 |
| [13] |
YUAN G L, LI T T, HU W J. A conjugate gradient algorithm for large-scale nonlinear equations and image restoration problems[J]. Applied Numerical Mathematics, 2020, 147: 129-141. DOI:10.1016/j.apnum.2019.08.022 |
| [14] |
ANDREI N. Another conjugate gradient algorithm with guaranteed descent and conjugacy conditions for Large-scale unconstrained optimization[J]. Journal of Optimization Theory and Applications, 2013, 159(1): 159-182. DOI:10.1007/s10957-013-0285-9 |
| [15] |
BROWN P N, SAAD Y. Convergence theory of nonlinear Newton-Krylov algorithms[J]. Siam Journal on Optimization, 1994, 4(2): 297-330. DOI:10.1137/0804017 |
| [16] |
YUAN G L. A new method with descent property for symmetric nonlinear equations[J]. Numerical Functional Analysis and Optimization, 2010, 31(8): 974-987. DOI:10.1080/01630563.2010.498599 |
| [17] |
YUAN G L, HU W J. A conjugate gradient algorithm for large-scale unconstrained optimization problems and nonlinear equations[J]. Journal of Inequalities and Applications, 2018, 2018(1): 113. DOI:10.1186/s13660-018-1703-1 |
| [18] |
DOLAN E D, MORÉ J J. Benchmarking optimization software with performance profiles[J]. Mathematical Programming, 2002, 91(2): 201-213. DOI:10.1007/s101070100263 |



