群智能优化算法是一类受自然界动物觅食方式等群体行为启发,为解决实际的最优化问题而提出的新计算方法。群智能优化算法可以很好地弥补传统优化算法的不足,有效处理复杂的现实问题。所以越来越多的学者从不同的生物现象上获取灵感,提出不同的群智能优化算法,例如:Mirjalili等[1]受樽海鞘链式聚集捕食行为启发,提出樽海鞘群算法(Salp Swarm Algorithm,SSA)。Arora等[2]根据蝴蝶觅食时传播的香味来帮助其他蝴蝶找到食物的现象提出蝴蝶优化算法(Butterfly Optimization Algorithm, BOA)。Xue等[3]根据麻雀的觅食行为和反捕食行为提出麻雀搜索算法(Sparrow Search Algorithm, SSA)。近年来,这些算法在路径规划、生产调度和图像处理等复杂优化问题上得到了广泛应用[4]。
金枪鱼群优化(Tuna Swarm Optimization,TSO)算法是由国内学者Xie等[5]于2021年提出的一种新的群智能优化算法,该算法受金枪鱼群体的两种觅食行为(螺旋式觅食和抛物线觅食)启发,具有较少的参数、良好的探索性和较高的寻优精度等特点,自提出以来,只经过短短一年的时间就被应用到了光伏电池参数优化[6]、风速数值预测[7]、风机故障分类[8]、图像分割[9]、Jensen模型参数求解[10]等多个领域,并取得不错的优化效果。
但是TSO算法与其他群智能优化算法一样,也有其不足,如在求解复杂问题时,前期收敛速度较慢,容易陷入局部最优等。针对这些不足,国内外的学者对其进行了相关改进,例如:Kumar等[6]用Tent混沌映射值作为TSO算法的权重跟随系数α1和α2,使TSO算法在跟随过程中有更大的搜索视野,从而提高其探索和开发能力;Tuerxun等[7]将TSO算法螺旋式觅食过程中参数a的值由原来的固定值改为随着迭代从1到0而逐渐减小的线性值,使得TSO算法在螺旋式觅食前期有较大的螺旋网而后期慢慢变小,进而更好地平衡算法全局搜索和局部开发的能力;Wang等[9]用分段函数Tent混沌映射值作为初始化种群的随机值,以提高初始化种群的丰富性,降低寻优过程中存在的误差,进而提高TSO算法的鲁棒性;胡丹等[11]引入高斯变异用于增强TSO算法局部搜索能力,进而帮助提高整体种群质量,加快TSO算法收敛速度。
综上所述,不同的改进方法虽然在一定程度上提高了TSO算法的性能,但是大多数改进策略都是对算法的参数进行改进,未涉及对金枪鱼觅食过程实质性的改进。为此,本研究提出混合策略改进的金枪鱼群优化算法(Improved Tuna Swarm Optimization Algorithm Based on Hybrid Strategy, HTSO),对TSO算法的初始化和螺旋式觅食做进一步的研究改进。
1 金枪鱼群优化(TSO)算法 1.1 初始化| $ X_i^{\mathrm{int}}=\operatorname{rand} \times(u b-l b)+l b, i=1, 2, \cdots, N P, $ | (1) |
其中,Xiint是第i个初始个体,ub和lb是搜索空间的上界和下界,NP是金枪鱼种群的数量,rand是0到1的随机向量。
1.2 螺旋式觅食群体中其他金枪鱼跟随最优个体进行螺旋式觅食的数学公式如下:
| $ \begin{array}{l} X_i^{t + 1} = \\ \left\{ {\begin{array}{*{20}{l}} {{\alpha _1} \times \left( {X_{{\rm{best }}}^t + \beta \times \left| {X_{{\rm{best }}}^t - X_i^t} \right|} \right) + {\alpha _2} \times X_i^t, }\\ {\quad i = 1}\\ {{\alpha _1} \times \left( {X_{{\rm{best }}}^t + \beta \times \left| {X_{{\rm{best }}}^t - X_i^t} \right|} \right) + {\alpha _2} \times X_{i - 1}^t, }\\ {\quad i = 2, 3, \cdots , NP} \end{array}, } \right. \end{array} $ | (2) |
| $ \alpha_1=a+(1-a) \times \frac{t}{t_{\max }}, $ | (3) |
| $ \alpha_2=(1-a)-(1-a) \times \frac{t}{t_{\max }}, $ | (4) |
| $ \beta=e^{b l} \times \cos (2 \pi b), $ | (5) |
| $ l=e^{3 \cos \left(\left(\frac{{t }_{\max }-t+1}{t_{\max }}\right) \times \pi\right)}, $ | (6) |
其中,Xit+1是第t+1次迭代的第i个个体,Xit是第t次迭代的第i个个体,Xi-1t是第t次迭代的第i-1个个体,Xbestt是当前最佳个体位置,α1和α2是控制个体向最佳个体和前一个个体移动趋势的权重系数,a是一个常数,t表示当前迭代次数,tmax表示最大迭代次数,b为均匀分布在0和1之间的随机数,e是常数,β是个体与最优个体或随机个体的距离参数,l是螺旋参数。
然而,当最优个体未能找到食物时,继续跟随最优个体不利于觅食,所以在搜索空间中随机生成一个坐标,作为螺旋搜索的参考点。其位置更新公式为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ X_i^{t + 1} = \\ \left\{ {\begin{array}{*{20}{l}} {{\alpha _1} \times \left( {X_{{\rm{rand }}}^t + \beta \times \left| {X_{{\rm{rand }}}^t - X_i^t} \right|} \right) + {\alpha _2} \times X_i^t, }\\ \ \ \ \ {i = 1}\\ {{\alpha _1} \times \left( {X_{{\rm{rand }}}^t + \beta \times \left| {X_{{\rm{rand }}}^t - X_i^t} \right|} \right) + {\alpha _2} \times X_{i - 1}^t, }\\ \ \ \ \ {i = 2, 3, \cdots , NP} \end{array}, } \right. \end{array} $ | (7) |
其中,Xrandt是第t迭代搜索空间中随机生成的参考点。
1.3 抛物线觅食金枪鱼除了螺旋式觅食外,还会进行抛物线觅食。这两种觅食方法交替使用,以提高金枪鱼捕获食物的概率,假设这两种方法随机选择,概率都为50%。具体的数学模型描述如下:
| $ \begin{array}{l} \ \ \ \ \ \ X_i^{t + 1} = \\ \left\{ {\begin{array}{*{20}{l}} {X_{{\rm{best }}}^t + {\mathop{\rm rand}\nolimits} \times \left( {X_{{\rm{best }}}^t - X_i^t} \right) + TF \times {p^2} \times }\\ \ \ \ \ {\left( {X_{{\rm{best }}}^t - X_i^t} \right), {\rm{ if rand }} < 0.5}\\ {TF \times {p^2} \times X_i^t, {\rm{ if rand }} \ge 0.5} \end{array}, } \right. \end{array} $ | (8) |
| $ p=\left(1-\frac{t}{t_{\max }}\right)^{\frac{t}{t_{\max }}}, $ | (9) |
其中,TF是-1或1的随机值,rand表示0到1之间的随机值,p是随迭代次数自适应变化参数,决定种群开发幅度。
在优化的过程中,TSO算法首先在搜索空间中随机生成金枪鱼种群。其次在迭代过程中每只金枪鱼个体随机选择两种觅食策略中的一种来执行,或者根据概率z选择在搜索空间中重新生成位置,z是一个常数。然后不断更新TSO算法的个体位置,直到满足终止条件,返回最佳个体和相应的适应度值。
2 混合策略改进的金枪鱼群优化算法(HTSO) 2.1 TSO存在的问题和改进思路通过分析公式(1)可以发现,公式(1)初始化的金枪鱼只能保证金枪鱼在上下界之间,但是在上下界之间金枪鱼的分布情况却是随机的,容易出现分布不均、扎堆在一起的现象,从而导致算法在实际寻优应用过程中出现误差大的情况。为此,本研究选用丰富性和遍历性较好的Circle混沌映射初始化金枪鱼种群,使其分布更均匀,进而降低算法在求解过程中存在的误差,避免出现极端的偶然结果。
通过对比分析公式(2)和公式(7)可以发现,在金枪鱼进行螺旋式觅食,种群中其他金枪鱼在最优个体没有找到食物时,可以选择空间中的随机坐标进行跟随移动,即将公式(2)中的Xbestt改为Xrandt从而得到公式(7)。面对实际复杂多维问题,金枪鱼选取跟随空间的随机值进行移动,这会使得算法在寻优求解的过程中有较大的概率陷入其局部最优解,不利于算法找到全局最优。所以,本研究选取有较大概率出现大跨步的莱维飞行(Levy flight)[12]提高金枪鱼在跟随空间随机位置的选择,帮助算法减少陷入局部极值的次数,进而提高算法在后期的寻优精度。
2.2 Circle混沌映射初始化种群常见的映射方法有Tent混沌映射、Logistic混沌映射、Circle混沌映射等,由于Circle混沌映射有较好的均匀性和遍历性,被研究得较多并应用到智能算法的改进上,例如:张达敏等[13]用嵌入Circle混沌映射改进鲸鱼优化算法(Whale Optimization Algorithm, WOA)的初始化种群,使初始化的鲸鱼个体在搜索空间分布更为均匀,从而提高算法的鲁棒性。宋立钦等[14]用改进的Circle混沌映射初始化种群,从而提高麻雀搜索算法的寻优能力。与随机初始化种群相比,通过Circle混沌映射的初始化种群分布更均匀,使得算法有更强的全局搜索能力,从而提高算法的寻优性能。所以本研究采用Circle混沌映射初始化金枪鱼种群,具体公式如下:
| $ x_{i+1}=\bmod \left(x_i+0.2-\left(\frac{0.5}{2 \pi}\right) \sin \left(2 \pi \cdot x_i\right), 1\right), $ | (10) |
其中,mod为求余函数,xi+1表示第i+1次映射的值。
2.3 Levy flight改进螺旋式觅食Levy flight指的是步长的概率分布为重尾分布的随机行走,就是说在随机行走的过程中有相对较高的概率出现大跨步,也就有更好的跳出局部最优的能力。所以Levy flight被不同的学者应用到群智能优化算法上,帮助算法增加全局搜索的能力。例如:马卫等[15]根据Levy flight扰动策略改进麻雀搜索算法,李阳等[16]用Levy flight和随机策略改进灰狼优化(Grey Wolf Optimizer, GWO)算法。再者,蜻蜓算法(Dragonfly Algorithm,DA)[17]和天鹰优化(Aquila Optimizer,AO)算法[18]也不同程度地融入了Levy flight的思想。基于以上分析,本研究用Levy flight改进金枪鱼螺旋式觅食,当金枪鱼群体中最优个体没有找到食物时,群体中其他金枪鱼根据Levy flight进行位置的更新,帮助TSO算法提升空间搜索能力和跳出局部最优能力,这将有助于找到全局最优。具体的数学公式如下:
| $ X_i^{t+1}=\left\{\begin{array}{l} k_1 \times X_i^t \times \operatorname{Levy}(D)+k_2 \times X_i^t, \\ \ \ \ \ i=1 \\ k_1 \times X_i^t \times \operatorname{Levy}(D)+k_2 \times X_{i-1}^t, \\ \ \ \ \ i=2, 3, \cdots, N P \end{array}, \right. $ | (11) |
| $ \operatorname{Levy}(x)=0.01 \times \frac{u}{|v|^{\frac{1}{\lambda}}}, $ | (12) |
其中,k1和k2是控制个体向Levy flight个体和前一个个体移动趋势的权重系数,k1和k2的值与1.2节中的α1和α2的值保持一致,D是位置向量的维数。λ的取值一般为[1, 3], 在本研究中λ=1.5;u和v服从公式(13)所示的正态分布,其中σu和σv由公式(14)求得。
| $ u \sim N\left(0, \sigma_u^2\right) \quad v \sim N\left(0, \sigma_v^2\right), $ | (13) |
| $ \sigma_u=\left\{\frac{\Gamma(1+\lambda) \sin \left(\frac{\pi \lambda}{2}\right)}{\lambda \times \Gamma\left(\frac{1+\lambda}{2}\right) \times 2^{\frac{(\lambda-1)}{2}}}\right\}^{\frac{1}{\lambda}}, \sigma_v=1, $ | (14) |
其中,N是正态分布。
| $ \mathit{\Gamma } = \int_0^{ + \infty } {{e^{ - t}}} {t^{x - 1}}{\rm{d}}t。$ | (15) |
基于上述章节对算法的改进,HTSO伪代码步骤如下。
输入:种群数量NP和最大迭代次数tmax
a.设置参数a和z的值,Circle混沌映射初始化种群Xiint。
b.计算金枪鱼的适应值,同时更新当前最优值金枪鱼个体。
c.对于所有金枪鱼个体,更新k1、k2和p的值并转至步骤d。
d.在[0, 1]产生随机数rand,并判断是否满足条件rand < z,若满足转至步骤e, 否则转至步骤f。
e.根据公式(1)来更新其他金枪鱼的位置。
f.再次判断是否满足条件rand < 0.5,若满足转至步骤h,否则转至步骤g。
g.根据公式(8)来更新金枪鱼的位置。
h.再一次判断是否满足条件t/tmax < rand,若满足转至步骤i,否则转至步骤j。
i.根据公式(11)来更新金枪鱼的位置。
j.根据公式(2)来更新金枪鱼的位置。
k.判断算法是否满足迭代的终止条件,若满足,则输出全局最优值;否则转至步骤c进行下一次迭代寻优。
输出:最优值
综上所述,HTSO具体流程如图 1所示。

|
| 图 1 HTSO流程图 Fig. 1 HTSO flow chart |
3 实验仿真与分析
为了验证本研究提出的改进策略对金枪鱼群优化算法寻优性能的提升效果,对其进行仿真实验,实验一共分为3个部分: ①对比实验分析。将HTSO与其他对比算法在不同的基准函数上进行寻优对比,分析改进后的算法是否有更强的寻优性能。②高维实验对比。由于实际问题往往复杂多维,所以在实验①的基础上进行高维寻优对比,以使算法更符合实际问题的求解。③ wilcoxon秩和检验。为了更好地比较改进后的算法与对比算法是否存在显著性差异,对各算法独立运行30次的结果进行wilcoxon秩和检验,进一步分析改进算法的有效性。
3.1 基准函数和实验环境 3.1.1 基准函数选取了14个基准函数进行实验,其中F1-F7为单峰函数,用于测试算法的开发能力;F8-F10为多峰函数,用于测试算法跳出局部最优的能力;F1-F10维数为D,F11-F14为固定维数函数(表 1)。维数越高、峰值越多,对于群智能算法的求解就越难,就越能体现出算法的寻优性能。
| 函数分类 Function classification |
测试函数 Test function |
维度 Dimension |
范围 Scope |
最优值 Optimal value |
| Unimodal test function | D | [-100, 100] | 0 | |
| D | [-10, 10] | 0 | ||
| D | [-100, 100] | 0 | ||
| D | [-100, 100] | 0 | ||
| D | [-30, 30] | 0 | ||
| D | [-100, 100] | 0 | ||
| D | [-1.28, 1.28] | 0 | ||
| Multimodal test function | D | [-32, 32] | 0 | |
| D | [-600, 600] | 0 | ||
| D | [-50, 50] | 0 | ||
| Fixed dimension test function | 2 | [-65, 65] | 0.998 | |
| 2 | [-5, 5] | 0.398 | ||
| 3 | [1, 3] | -3.86 | ||
| 4 | [0, 10] | -10.153 |
3.1.2 实验环境
整个实验是在Matlab R2018a中进行,计算机操作系统为Windows 11,处理器Inter(R) Core(TM) i7-11800H,运行内存16 GB。
3.2 结果与分析 3.2.1 对比实验分析为了充分验证HTSO的寻优性能和跳出局部最优的能力,选择近年来应用范围广且应用性能较好的鲸鱼优化算法[19]、灰狼优化算法[20]和哈里斯鹰优化(Harris Hawks Optimization, HHO)算法[21]作为对比算法。为了保证公平,所有实验在相同环境下进行。
设置种群数为30,最大迭代数为500,维度D=30,对比算法的其他参数与原文献保持一致。在HTSO中z=0.05, a=0.7,与文献[5]中的TSO算法保持一致。选取平均值(Mean)和标准差(Std)作为算法性能的度量标准。因为平均值可以用于说明算法的求解精度,标准差可以用于衡量算法的鲁棒性[22]。各算法分别独立运行30次,记录运行结果并且对其进行最优值排名(Rank),具体见表 2。为了更加直观地展现出对比算法的收敛情况,图 2-7给出了部分对比算法的收敛曲线。
| 函数 Function |
最优值 Optimal value |
统计值 Statistical value |
HTSO | TSO | GWO | WOA | HHO |
| F1 | 0 | Mean | 0 | 2.9526e-230 | 1.0097e-27 | 8.3689e-74 | 1.6024e-93 |
| Std | 0 | 0 | 1.3595e-27 | 2.3083e-73 | 7.7342e-93 | ||
| Rank | 1 | 2 | 5 | 4 | 3 | ||
| F2 | 0 | Mean | 2.0113e-206 | 2.6965e-116 | 8.5985e-17 | 1.1607e-51 | 1.0710e-50 |
| Std | 0 | 9.6055e-116 | 6.5733e-17 | 2.6196e-51 | 3.5828e-50 | ||
| Rank | 1 | 2 | 5 | 3 | 4 | ||
| F3 | 0 | Mean | 0 | 2.633e-209 | 1.7720e-05 | 4.2343e+04 | 6.7658e-71 |
| Std | 0 | 0 | 4.7681e-05 | 1.6273e+04 | 3.7034e-70 | ||
| Rank | 1 | 2 | 4 | 5 | 3 | ||
| F4 | 0 | Mean | 4.0866e-207 | 3.4640e-115 | 7.2688e-07 | 4.3731e+01 | 6.9136e-49 |
| Std | 0 | 1.6103e-114 | 6.7944e-07 | 2.8172e+01 | 3.4118e-48 | ||
| Rank | 1 | 2 | 4 | 5 | 3 | ||
| F5 | 0 | Mean | 1.6456e-03 | 3.7951 | 2.7062e+01 | 2.7871e+01 | 2.3835e-02 |
| Std | 2.7085e-03 | 8.7646 | 8.1582e-01 | 4.9587e-01 | 2.8054e-02 | ||
| Rank | 1 | 3 | 4 | 5 | 2 | ||
| F6 | 0 | Mean | 9.3541e-06 | 1.1054e-04 | 6.7524e-01 | 3.9062e-01 | 2.0627e-04 |
| Std | 1.2444e-05 | 1.5088e-04 | 2.9623e-01 | 2.5590e-01 | 3.1725e-04 | ||
| Rank | 1 | 2 | 5 | 4 | 3 | ||
| F7 | 0 | Mean | 9.0588e-05 | 4.5670e-04 | 2.0095e-03 | 2.7779e-03 | 1.1901e-04 |
| Std | 1.0082e-04 | 4.9745e-04 | 1.1233e-03 | 2.2340e-03 | 1.0448e-04 | ||
| Rank | 1 | 3 | 4 | 5 | 2 | ||
| F8 | 0 | Mean | 8.8818e-16 | 8.8818e-16 | 9.9061e-14 | 4.6777e-15 | 8.8818e-16 |
| Std | 0 | 0 | 1.6334e-14 | 2.6279e-15 | 0 | ||
| Rank | 1 | 1 | 3 | 2 | 1 | ||
| F9 | 0 | Mean | 0 | 0 | 2.8054e-03 | 2.1539e-02 | 0 |
| Std | 0 | 0 | 8.3868e-03 | 6.8921e-02 | 0 | ||
| Rank | 1 | 1 | 2 | 3 | 1 | ||
| F10 | 0 | Mean | 8.2098e-06 | 2.9674e-03 | 6.6430e-01 | 5.7124e-01 | 9.0763e-05 |
| Std | 1.2087e-05 | 5.6517e-03 | 2.7471e-01 | 2.8535e-01 | 1.1052e-04 | ||
| Rank | 1 | 3 | 5 | 4 | 2 | ||
| F11 | 0.998 | Mean | 0.9980 | 0.9980 | 3.9710 | 2.0194 | 1.2618 |
| Std | 2.7195e-16 | 2.6562e-16 | 3.9079 | 1.7087 | 0.9320 | ||
| Rank | 2 | 1 | 5 | 4 | 3 | ||
| F12 | 0.398 | Mean | 3.9789e-01 | 3.9789e-01 | 3.9789e-01 | 3.9789e-01 | 3.9790e-01 |
| Std | 0 | 3.2434e-16 | 2.6094e-06 | 9.8163e-06 | 1.4175e-05 | ||
| Rank | 2 | 3 | 4 | 5 | 1 | ||
| F13 | -3.86 | Mean | -3.8628 | -3.8628 | -3.8612 | -3.8533 | -3.8603 |
| Std | 2.3829e-15 | 2.3958e-15 | 2.6245e-02 | 1.0144e-02 | 3.3838e-03 | ||
| Rank | 3 | 4 | 2 | 5 | 1 | ||
| F14 | -10.153 | Mean | -10.1532 | -10.1532 | -10.1514 | -7.6707 | -5.1989 |
| Std | 4.9369e-15 | 4.9589e-15 | 1.005e-03 | 2.6919 | 8.1597 e-01 | ||
| Rank | 1 | 2 | 3 | 4 | 5 |
|
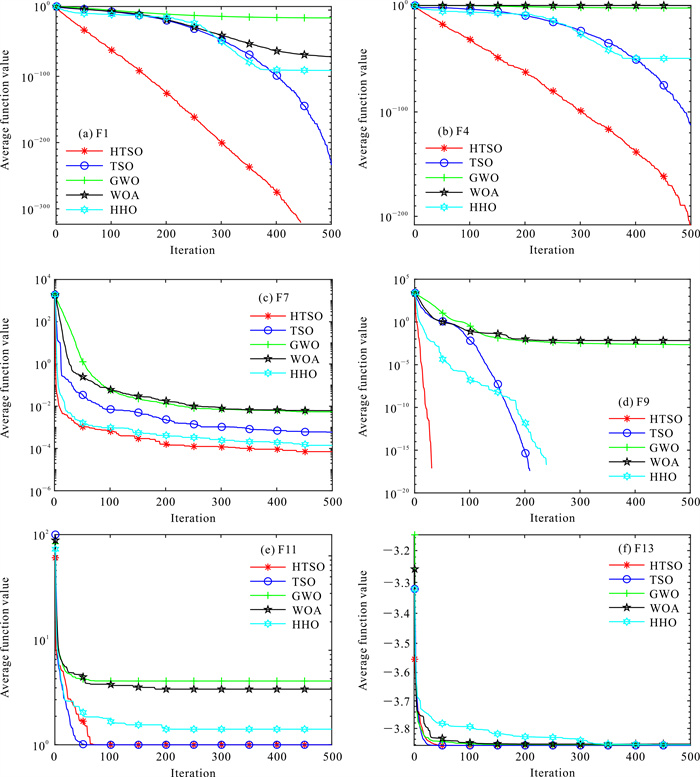
| 图 2 F1、F4、F7、F9、F11和F13函数的收敛曲线 Fig. 2 Convergence curve of F1, F4, F7, F9, F11 and F13 function |
由表 2可以得出,从宏观上,在14个测试的基准函数中,有11个函数的HTSO寻优精度排名第一,而传统的TSO算法只有3个函数寻优结果排名第一,GWO算法、WOA和HHO算法分别有0次、0次和4次寻优结果最优,可见HTSO的寻优精度明显高于传统TSO算法和其他3种对比算法。再者,在各算法独立运行30次的过程中,HTSO的标准差有13次是最小的,其中有7次标准差为0,明显优于其他4种对比算法,可以看出HTSO有较好的稳定性和鲁棒性。
从微观上,对于7个单峰函数F1-F7,HTSO排名均为第一,且明显优于传统的TSO算法,说明改进后的算法比原来的算法具有更强的开发能力。对于3个多峰测试函数F8-F10,HTSO排名也均为第一,函数F8和F9,HTSO、TSO算法和HHO算法并列第一,对于F10,HTSO明显优于传统的TSO算法和其他算法,由此可以说明,HTSO有更强的能力跳出局部最优,找到全局的最优值。对于固定维数的4个测试函数F11-F14,HTSO与传统TSO算法虽然寻优精度相差不大,但是HTSO有3次排名优于传统的TSO算法,可以看出HTSO在面对复杂固定维数函数时仍然有较强的寻优性能。
从图 2可以很清楚地看出,对于函数F1、F4和F9,HTSO收敛速度明显比传统的TSO算法和其他算法快,并且有更高的寻优精度。对于函数F7,HTSO的收敛精度和收敛速度也都以微弱的优势优于其他算法。对于函数F11,HTSO的收敛速度虽然不如TSO算法快,但是收敛精度和TSO算法保持一致,且也优于其他对比算法。对于函数F13,HTSO的收敛精度与TSO算法基本保持一致。
综上可知,HTSO的标准差是最小的,说明Circle映射初始化种群改进策略的正确性和有效性。从图 2可以看出,HTSO有更快的收敛速度和更好的寻优精度,说明Levy flight改进策略能帮助算法减少陷入局部最优次数。
3.2.2 高维实验对比通过上述分析可以看出,HTSO在低维的时候有较强的寻优能力,但是在实际中,问题的规模往往比较复杂,单纯测试算法在低维时的性能是远远不够的,所以为了说明HTSO的实用性,将5种算法在50维和100维测试函数上进行对比,其余保持不变,分别独立运行30次,取其平均值,结果见表 3,字体加粗部分为5种算法中寻优结果最好的函数值。
| 函数 Function |
维数 Dimension |
HTSO | TSO | GWO | WOA | HHO |
| F1 | 50 | 0 | 5.3393e-228 | 8.1469e-20 | 4.0863e-73 | 1.6749e-95 |
| 100 | 0 | 6.7693e-228 | 1.7026e-12 | 6.6193e-71 | 6.6349e-96 | |
| F2 | 50 | 4.5330e-207 | 2.7757e-116 | 2.5325e-12 | 5.3816e-50 | 2.3497e-50 |
| 100 | 3.3015e-203 | 2.4115e-113 | 3.4114e-08 | 2.5631e-50 | 1.2749e-49 | |
| F3 | 50 | 0 | 2.2206e-212 | 1.7298e-01 | 2.0626e+05 | 7.1750e-69 |
| 100 | 0 | 5.3853e-203 | 5.3903e+02 | 1.0508e+06 | 2.7236e-56 | |
| F4 | 50 | 1.2468e-200 | 1.6344e-112 | 5.2376e-04 | 7.1155e+01 | 1.2114e-48 |
| 100 | 2.2388e-204 | 3.8186e-111 | 7.6884e-01 | 8.4627e+01 | 3.0200e-48 | |
| F5 | 50 | 7.7253e-03 | 5.6084e-01 | 4.7349e+01 | 4.8261e+01 | 2.5280e-02 |
| 100 | 1.0982e-01 | 9.9755e-01 | 9.7751e+01 | 9.8194e+01 | 3.1969e-02 | |
| F6 | 50 | 2.6491e-04 | 8.5107e-03 | 2.6974 | 1.2175 | 2.0210e-04 |
| 100 | 3.3258e-03 | 6.8805e-02 | 1.0184e+01 | 4.2050 | 3.6320e-04 | |
| F7 | 50 | 8.0477e-05 | 3.0993e-04 | 3.2150e-03 | 3.4020e-03 | 9.9828e-05 |
| 100 | 1.3013e-04 | 4.1051e-04 | 6.5696e-03 | 3.7251e-03 | 1.3730e-04 | |
| F8 | 50 | 8.8818e-16 | 8.8818e-16 | 3.4925e-11 | 4.5593e-15 | 8.8818e-16 |
| 100 | 8.8818e-16 | 8.8818e-16 | 1.2647e-07 | 4.0856e-15 | 8.8818e-16 | |
| F9 | 50 | 0 | 0 | 4.1447e-03 | 5.6155e-03 | 0 |
| 100 | 0 | 0 | 4.2065e-03 | 8.4813e-03 | 0 | |
| F10 | 50 | 1.3038e-04 | 7.6139e-04 | 2.1126 | 1.1851 | 1.6841e-04 |
| 100 | 7.2873e-04 | 4.4557e-03 | 6.8032 | 2.7710 | 1.5530e-04 |
从表 3可以看出,测试函数F1-F10在50维下,HTSO有9次是寻优结果最好的算法,在100维中,HTSO有7次是寻优结果最好的算法。对于F6和F10,虽然HTSO的寻优精度不是最优,但是也仅次于HHO算法,排名第二。对于测试函数F1-F4,其他4种算法在高维下寻优精度下降较快,但是HTSO依然可以保持较高的精度。综上分析可知,在高维情况下HTSO仍然能保持优秀的寻优性能,说明在高维情况下,Circle映射和Levy flight改进策略对算法的改进也是有效的,验证了HTSO的实用性。
3.2.3 wilcoxon秩和检验对14个基准函数独立运行30次,取其平均值和标准差虽然能在一定程度上说明不同算法的寻优性能和寻优精度,但是不能说明HTSO与其他算法是否存在显著性差异。鉴于此,本研究采用wilcoxon秩和检验来判断不同算法整体的结果是否有显著性差异。将HTSO与其他4种算法独立运行30次的结果作为样本,在置信度0.05的条件下进行检验,当wilcoxon秩和检验的P值小于0.05时,即有95%的概率相信,两种对比的算法存在显著性差异; 当wilcoxon秩和检验的P值大于0.05时,则说明两种对比算法在整体的寻优结果上差异不大,其中Nan表示两组样本基本相同。具体的wilcoxon秩和检验的P值见表 4。
| 函数 Function |
TSO | GWO | WOA | HHO |
| F1 | 1.21e-12 | 1.21e-12 | 1.21e-12 | 1.21e-12 |
| F2 | 3.02e-11 | 3.02e-11 | 3.02e-11 | 3.02e-11 |
| F3 | 1.21e-12 | 1.21e-12 | 1.21e-12 | 1.21e-12 |
| F4 | 3.02e-11 | 3.02e-11 | 3.02e-11 | 3.02e-11 |
| F5 | 4.71e-04 | 3.02e-11 | 3.02e-11 | 1.87e-07 |
| F6 | 1.41e-04 | 3.01e-11 | 3.01e-11 | 2.32e-06 |
| F7 | 3.01e-07 | 3.34e-11 | 1.61e-10 | 2.12e-01 |
| F8 | Nan | 1.13e-12 | 4.04e-09 | Nan |
| F9 | Nan | 4.19e-02 | 4.19e-02 | Nan |
| F10 | 3.83e-05 | 3.02e-11 | 3.02e-11 | 2.49e-06 |
| F11 | 7.21e-01 | 2.37e-11 | 2.37e-11 | 2.88e-11 |
| F12 | 3.34e-01 | 1.22e-12 | 1.22e-12 | 1.22e-12 |
| F13 | 8.83e-01 | 1.82e-11 | 1.82e-11 | 1.82e-11 |
| F14 | 8.81e-01 | 1.33e-11 | 1.33e-11 | 1.33e-11 |
从表 4可以看出,在14个基准测试函数中,对比HTSO与传统TSO算法的寻优结果,有8个测试函数存在显著性差异;对比HTSO与HHO算法的寻优结果,有11个测试函数存在显著性差异;HTSO与其他2种算法的寻优结果对比都存在显著性差异。综上所述,将HTSO与其他4种算法的寻优结果对比,有一半以上的测试函数存在显著性差异,由此可推测HTSO与其他4种对比算法的寻优结果有显著性差异。
4 结论TSO算法是近年来提出的一种元启发式算法,针对该算法在前期收敛速度较慢、容易陷入局部最优和鲁棒性差等不足,本研究提出HTSO。首先,用Circle映射初始化金枪鱼,提高初始种群的丰富性,使初始化的金枪鱼分布更均匀,从而降低TSO算法求解的误差,提高算法的鲁棒性;其次,用Levy flight改进螺旋式觅食,增大鱼群中最优个体在未找到食物时随机选取一个参考点的幅度,进而减少TSO算法陷入局部最优的次数,提高TSO算法寻优精度;最后通过3个仿真实验(与其他4种算法寻优对比、高维实验分析、wilcoxon秩和检验)验证HTSO的性能。实验结果表明,本研究提出的改进策略是有效的且与第2节的分析相吻合,HTSO有更好的鲁棒性,更高的跳出局部最优的能力和寻优精度。在今后的研究中,计划将HTSO应用到物流配送路径优化上,通过实际问题进一步验证HTSO的性能。
| [1] |
MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. DOI:10.1016/j.advengsoft.2017.07.002 |
| [2] |
ARORA S, SINGH S. Butterfly optimization algorithm: a novel approach for global optimization[J]. Soft Computing, 2019, 23(3): 715-734. DOI:10.1007/s00500-018-3102-4 |
| [3] |
XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
| [4] |
李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究[J]. 计算机工程与应用, 2020, 56(22): 1-12. DOI:10.3778/j.issn.1002-8331.2006-0291 |
| [5] |
XIE L, HAN T, ZHOU H, et al. Tuna swarm optimization: a novel swarm-based metaheuristic algorithm for global optimization[J]. Computational Intelligence and Neuroscience, 2021, 2021: 1-22. |
| [6] |
KUMAR C, MAGDAKLIN MARY D. A novel chaotic-driven Tuna Swarm Optimizer with Newton-Raphson method for parameter identification of three-diode equivalent circuit model of solar photovoltaic cells/modules[J]. Optik, 2022, 264: 1-22. |
| [7] |
TUERXUN W, XU C, GUO H Y, et al. An ultra-short-term wind speed prediction model using LSTM based on modified tuna swarm optimization and successive variational mode decomposition[J]. Energy Science & Engineering, 2022, 10: 3001-3022. |
| [8] |
TUERXUN W, XU C, GUO H Y, et al. Fault classification in wind turbine based on deep belief network optimized by modified tuna swarm optimization algorithm[J]. Journal of Renewable and Sustainable Energy, 2022, 14(3): 033307. |
| [9] |
WANG J Y, ZHU L K, WU B W, et al. Forestry canopy image segmentation based on improved tuna swarm optimization[J]. Forests, 2022, 13(11): 1-18. |
| [10] |
薛萍, 刘玲, 王仰仁, 等. 基于金枪鱼群优化算法的Jensen模型参数求解[J]. 灌溉排水学报, 2022, 41(11): 22-29. |
| [11] |
胡丹, 杨书恒. 基于改进金枪鱼算法优化ELM模型的光伏功率预测[J]. 武汉理工大学学报, 2022, 44(8): 97-104. |
| [12] |
VISWANATHAN G M, AFANASYEV V, BULDY-REV S V, et al. Levy flights search patterns of biological organisms[J]. Physica A, 2001, 295(1): 85-88. |
| [13] |
张达敏, 徐航, 王依柔, 等. 嵌入Circle映射和逐维小孔成像反向学习的鲸鱼优化算法[J]. 控制与决策, 2021, 36(5): 1173-1180. |
| [14] |
宋立钦, 陈文杰, 陈伟海, 等.基于混合策略的麻雀搜索算法改进及应用[J/OL].北京航空航天大学学报, (2022-01-25)[2022-02-02].https://kns.cnki.net/kcms/detail/11.2625.V.20220121.1826.001.html. DOI: 10.13700/j.bh.1001-5965.2021.0629.
|
| [15] |
马卫, 朱娴. 基于莱维飞行扰动策略的麻雀搜索算法[J]. 应用科学学报, 2022, 40(1): 116-130. |
| [16] |
李阳, 李维刚, 赵云涛, 等. 基于莱维飞行和随机游动策略的灰狼算法[J]. 计算机科学, 2020, 47(8): 291-296. |
| [17] |
MIRJALILI S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural Computing and Applications, 2016, 27(4): 1053-1073. |
| [18] |
ABUALIGAH L, YOUSRI D, ABD ELAZIZ M, et al. Aquila optimizer: a novel meta-heuristic optimization algorithm[J]. Computers and Industrial Engineering, 2021, 157: 1-37. |
| [19] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. |
| [20] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61. |
| [21] |
HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization: algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849-872. |
| [22] |
汤安迪, 韩统, 徐登武, 等. 混沌多精英鲸鱼优化算法[J]. 北京航空航天大学学报, 2021, 47(7): 1481-1494. |



