2. 北部湾大学海洋学院, 广西北部湾海洋环境变化与灾害研究重点实验室, 广西钦州 535011;
3. 钦州市海洋环境监测预报中心, 广西钦州 535000
2. Guangxi Key Laboratory of Marine Environmental Change and Disaster in Beibu Gulf, Ocean College, Beibu Gulf University, Qinzhou, Guangxi, 535011, China;
3. Qinzhou Marine Environment Monitoring and Forecasting Center, Qinzhou, Guangxi, 535000, China
钦州湾位于北部湾北部,由内湾(茅尾海)和外湾(钦州湾)两部分构成,整体呈哑铃状,南面与北部湾相连,东、西、北三面被陆地环绕,属于溺谷型海湾[1]。钦州湾是我国西南部与东盟国家的一个重要通道,是我国“一带一路”和“国际贸易陆海新通道”的枢纽,是国家战略布局的重要区域,具有重要的经济和战略地位。潮汐是钦州湾的主要海洋动力,对航海运输、港口作业、水交换能力、水产养殖和生态保护等都具有重要影响。另外,潮汐的研究也是钦州湾主要海洋灾害——风暴潮的研究基础,因此受到了学者们的广泛关注。
近年来,有不少学者对钦州湾海域的潮汐、潮流进行了研究,李树华[2]基于一种阶梯式网格对钦州湾潮汐潮流进行数值计算,结果显示,整个钦州湾以全日潮为主,全日潮振幅比半日潮振幅大1倍左右;孙洪亮等[3, 4]利用观测数据分析和数值研究等方法对钦州湾的潮汐性质进行分析,认为广西近海的潮汐性质基本属于正规全日潮;董德信等[5]利用冬、夏两个季节实测潮流调查数据研究了钦州湾潮流的季节变化特征,认为钦州湾属不规则全日潮海区,潮流运动形式为往复流,落潮流速一般大于涨潮流速;张伯虎等[6]利用“908”专项调查的验潮资料,进一步对防城港、涠洲岛等广西沿岸重点港湾进行潮型与潮汐特征分析,初步揭示了广西沿岸海域大潮的发生周期及其变化规律;宋德海等[7]基于FVCOM(Finite-Volume Coastal Ocean Model)模式,建立钦州湾三维潮流数值模型,重现了钦州湾的潮位和潮流变化状况,计算得到了更精细的K1、O1、M2、S2 4个分潮的振幅和迟角;赵昌等[8]利用普林斯顿海洋模型(Princeton Ocean Model,POM)分析了北部湾及其临海海区的潮汐特征。
潮汐不对称性是港湾潮汐的一个重要特征,对物质输运、港湾稳定性、地形变化等都有重要影响。Nidzieko[9]利用偏度的定义,量化分析了潮汐不对称性。Song等[10]对Nidzieko的方法进行了拓展和推广,提出了一个可以识别任何潮汐时间序列中造成不对称成分的一般框架。根据这些方法,国内学者对不同地区的潮汐不对称性作出了定量分析。李谊纯等[11, 12]对浙江省瓯江口和广西防城港海域进行了潮汐不对称性偏度分析;李谊纯等[13, 14]推导出一种潮流不对称的计算方法,并应用于北仑河口和涠洲岛,结果表明北仑河口O1/K1/M2分潮组合和余流是潮流不对称贡献最大的两个因素;林国尧等[15]研究了海南莺歌海潮汐不对称性机理;童朝锋等[16]定量分析了海南红塘湾潮汐不对称性;陈云等[17]对长江口新桥水道潮汐不对称性进行分析,结果显示该水道潮汐不对称性受余流与各分潮的相互作用、天文潮之间的相互作用影响。目前对钦州湾潮汐不对称性的研究相对较少,李树华[18]利用周日连续潮流观测数据对钦州湾湾口附近的涨、落潮历时作了分析,结果显示该地区涨潮历时大于落潮历时,其差值在2 h以上;吕赫等[19]利用FVCOM模式,模拟了钦州湾潮汐、潮流,并利用偏度分析了钦州湾潮汐的不对称性,结果显示落潮占优。
上述研究利用观测和数值模拟的方法对钦州湾潮汐、潮流基本特征及不对称性进行了分析,虽然取得了较好的研究成果,但是这些研究除了数值模拟研究外,所使用的观测数据样本长度都比较短,许多研究仅使用了1-2 d的观测数据。短时间的观测数据容易受天气等因素的扰动,具有一定的随机性,而潮汐除了有半日/全日的周期变化外,还有年际和年代际的变化周期,这些特征对港口建设都具有重要意义。目前对钦州湾潮汐的长期变化特征尚未清楚,因此本研究基于钦州湾验潮站2008—2020年共13年的逐时观测水位数据资料,研究钦州湾潮汐长时间变化特征,拟为钦州湾的沿海经济、港口工程建设和防灾减灾提供科学依据。
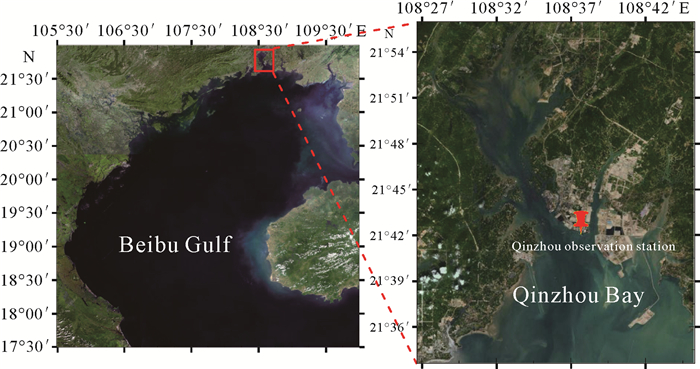
1 材料与方法 1.1 数据来源和研究区域本研究收集整理了钦州湾2008—2020年共13年的逐时观测水位数据资料,数据来源于钦州市海洋环境监测站,观测点坐标为21°41′N,108°37′E(图 1)。该数据从钦州本地的水位基准面起算,基准点的水位是85高程+2.62 m。所使用的仪器为GPH500型潮位传感器。由于钦州湾海域面积小,潮汐要素区域差异不大,同时观测站位于钦州湾中部,其观测的潮位特征在一定程度上可以代表钦州湾的潮汐特征。
|
| 图 1 钦州湾潮位观测站位置[地图底图引自天地图,审图号为GS(2022)3124号] Fig. 1 Location of tidal level observation station in Qinzhou Bay (The base map is taken from map world, and the drawing review number is GS(2022)3124) |
1.2 方法 1.2.1 潮汐调和分析
根据潮汐理论,潮水位可以由多个分潮线性叠加而成,公式如下:
| $\zeta(t)=S_0+\sum\limits_{i=1}^n\left[H_i \cos \left(\sigma_i t-g_i\right)\right]+\varepsilon(t), $ | (1) |
其中,ζ(t)为t时刻的观测水位,S0为观测期间的平均海面,n为分潮个数,Hi、σi、gi分别为分潮的振幅、频率和迟角,ε(t)为非天文潮因素引起的水位变化。Pawlowicz等[20]于2002年提出T_TIDE程序包,具有节点校正、推理等功能,可以对观测水位数据进行潮汐调和分析和预报。该程序包自发布以来,已得到广泛的运用和可行性验证[21]。本研究采用T_TIDE v1.3beta程序包,对观测数据质量控制后进行调和分析,选取其中的11个显著分潮Q1、O1、P1、K1、N2、M2、S2、K2、M4、MS4、M6进行分析和讨论。
1.2.2 潮汐类型为了量化潮汐类型,我国以K1和O1两个全日分潮的振幅之和与半日分潮M2振幅的比值大小作为指标,称为潮汐类型数(F),则
| $F=\frac{H_{\mathrm{K}_1}+H_{\mathrm{O}_1}}{H_{\mathrm{M}_2}}, $ | (2) |
当F<0.5时,为规则半日潮;当0.5≤F<2.0时,为不规则半日潮;当2.0≤F≤4.0时,为不规则全日潮;当F>4.0时,为规则全日潮[22]。
1.2.3 潮汐偏度根据Nidzieko[9]提出的从统计学角度定量分析潮汐不对称性的方法,偏度γ的计算公式如下:
| $\gamma=\frac{\frac{1}{\tau-1} \sum\limits_{t=1}^\tau\left(\zeta_t^{\prime}-\overline{\zeta^{\prime}}\right)^3}{\left[\frac{1}{\tau-1} \sum\limits_{t=1}^\tau\left(\zeta^{\prime}{ }_t-\overline{\zeta^{\prime}}\right)^2\right]^{\frac{3}{2}}}, $ | (3) |
其中,
Song等[10]对Nidzieko[9]提出的方法进行拓展和推广,发现对于长时间的潮汐不对称性,无论其中包含多少个显著的分潮,有且仅有满足2ω1=ω2的2个分潮组合或ω1+ω2=ω3的3个分潮组合能导致长时间的不对称性,故提出了满足2种或3种特定分潮组合的偏度公式:
| $\gamma_2=\frac{\frac{3}{4} a_1^2 \omega_1^2 a_2 \omega_2 \sin \left(2 \varphi_1-\varphi_2\right)}{\left[\frac{1}{2}\left(a_1^2 \omega_1^2+a_2^2 \omega_2^2\right)\right]^{\frac{3}{2}}}, $ | (4) |
| $\gamma_3=\frac{\frac{3}{2} a_1 \omega_1 a_2 \omega_2 a_3 \omega_3 \sin \left(\varphi_1+\varphi_2-\varphi_3\right)}{\left[\frac{1}{2}\left(a_1^2 \omega_1^2+a_2^2 \omega_2^2+a_3^2 \omega_3^2\right)\right]^{\frac{3}{2}}}, $ | (5) |
其中,a、ω、φ分别为分潮的振幅、频率和迟角。
为了计算特定分潮组合对潮汐偏度的贡献,用β表示由2个或3个特定分潮组合对潮汐偏度的贡献,公式表示如下:
| $\beta_2=\gamma_2 \times\left(\frac{a_1^2 \omega_1^2+a_2^2 \omega_2^2}{\sum\limits_{i=1}^N a_i^2 \omega_i^2}\right)^{\frac{3}{2}}, $ | (6) |
| $\beta_3=\gamma_3 \times\left(\frac{a_1^2 \omega_1^2+a_2^2 \omega_2^2+a_3^2 \omega_3^2}{\sum\limits_{i=1}^N a_i^2 \omega_i^2}\right)^{\frac{3}{2}} 。$ | (7) |
潮汐的总偏度可以表示如下:
| $\gamma_N=\sum \beta, $ | (8) |
其中,N为分潮个数。当γ或者β小于0时,涨潮时间长,落潮时间短,落潮流速大于涨潮流速,对应落潮流占优;反之,当γ或者β大于0时,落潮时间长,涨潮时间短,涨潮流速大于落潮流速,对应涨潮流占优。
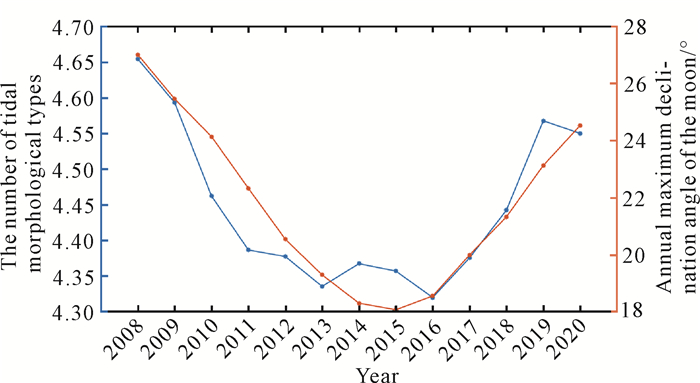
2 结果与分析 2.1 潮汐类型根据公式(2),利用观测站逐时观测水位数据计算了钦州湾2008—2020年逐年的潮汐类型数(图 2)。钦州湾潮汐类型数不是恒定不变的,而是有明显的年际变化特征。2008—2020年,钦州湾潮汐类型数最低为2016年的4.320,最高为2008年的4.654,均大于4.000,表示其为规则全日潮类型。为了进一步分析月赤纬角变化对潮汐类型数的影响,结合金朝辉等[23]的研究绘制了同期年最大月赤纬角逐年变化曲线(图 2)。将潮汐类型数和年最大月赤纬角作相关性分析,在0.05显著性水平下,相关系数达0.92,表明潮汐类型数和年最大月赤纬角存在强相关关系。
|
| 图 2 钦州湾潮汐类型数与年最大月赤纬角 Fig. 2 Number of tidal morphological types and the annual maximum declination angle of the moon in Qinzhou Bay |
2.2 潮汐特征
根据潮水位数据调和分析结果,钦州湾以O1、K1分潮占优,O1振幅略大于K1振幅,约是M2分潮振幅的2倍,与2.1节的钦州湾潮汐类型数F>4.0相对应。
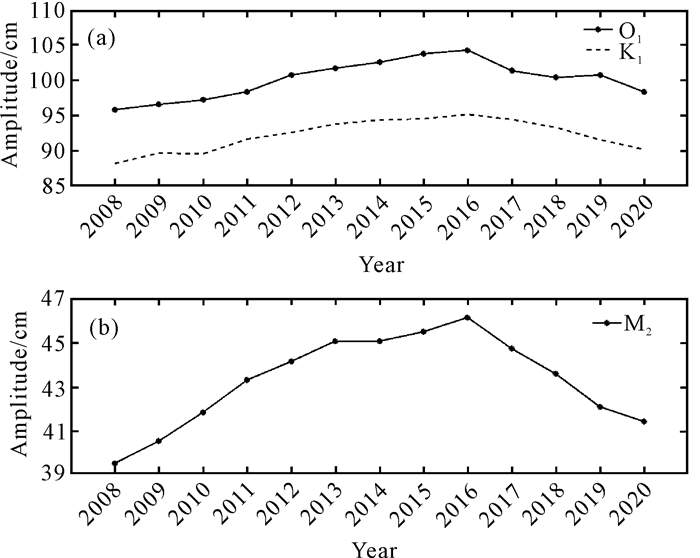
表 1为2008年11个主要分潮的振幅和迟角。图 3为振幅较大的3个分潮O1、K1和M2的年际变化曲线,这3个主要分潮振幅都有相似的变化规律,均在2008年振幅为最小值,其中O1为95.82 cm,K1为88.18 cm,M2为39.53 cm;其后呈逐年增大趋势,至2016年达到最大值,其中O1为104.27 cm,K1为95.15 cm,M2为46.16 cm;而后逐渐下降,呈单峰振荡形态。对比图 2显示的年最大月赤纬角的逐年变化曲线,月赤纬角在2008年最大,2015年最小,O1、K1和M2 3个分潮振幅的变化与月赤纬角相反。月赤纬角在2008—2020年与O1、K1、M2分潮振幅呈强负相关关系(表 2),由此推断潮汐的振幅变化与月赤纬角的变化有关。
| 分潮 Tidal constituents |
振幅/cm Amplitude/cm |
迟角/° Phase lag/° |
分潮 Tidal constituents |
振幅/cm Amplitude/cm |
迟角/° Phase lag/° |
|
| Q1 | 20.54 | 6.73 | N2 | 8.17 | 144.18 | |
| O1 | 95.82 | 38.09 | M2 | 39.53 | 186.50 | |
| P1 | 26.05 | 91.53 | S2 | 9.42 | 244.74 | |
| K1 | 88.18 | 100.23 | K2 | 7.54 | 260.60 | |
| M4 | 1.97 | 21.17 | MS4 | 1.50 | 38.95 | |
| M6 | 0.38 | 237.04 |
|
| 图 3 O1、K1、M2分潮的振幅变化 Fig. 3 Amplitude variations of O1, K1 and M2 tidal constituent |
| 分潮 Tidal constituents |
相关系数 Correlation coefficient |
P值 P values |
95%置信区间 95% confidence interval |
| O1 | -0.945 8 | 1.043 2×10-6 | -0.984 0—-0.824 5 |
| K1 | -0.972 0 | 2.926 5×10-8 | -0.991 8—-0.906 4 |
| M2 | -0.987 4 | 3.741 5×10-10 | -0.996 3—-0.957 1 |
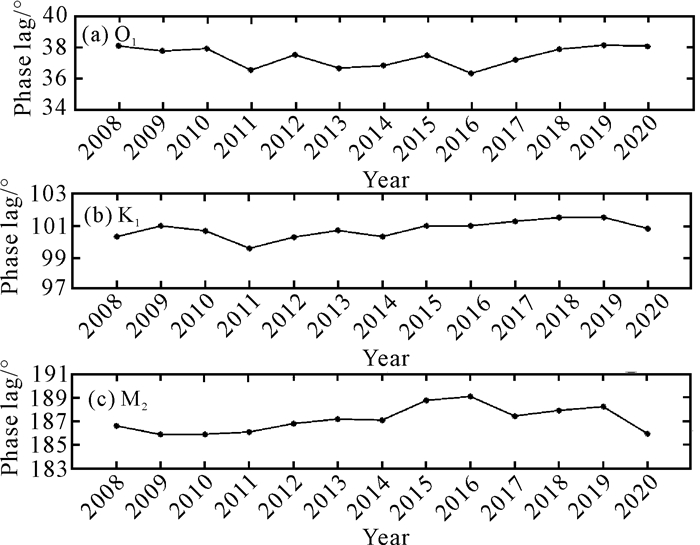
2008—2020年各分潮的迟角略有变化,其中O1分潮迟角为36.33°-38.14°,K1分潮迟角为99.48°-101.48°,M2分潮迟角为185.75°-189.01°,且M2分潮的迟角在2016年最大(图 4)。
|
| 图 4 O1、K1、M2分潮的迟角变化 Fig. 4 Variations of phase lag for O1, K1 and M2 tides |
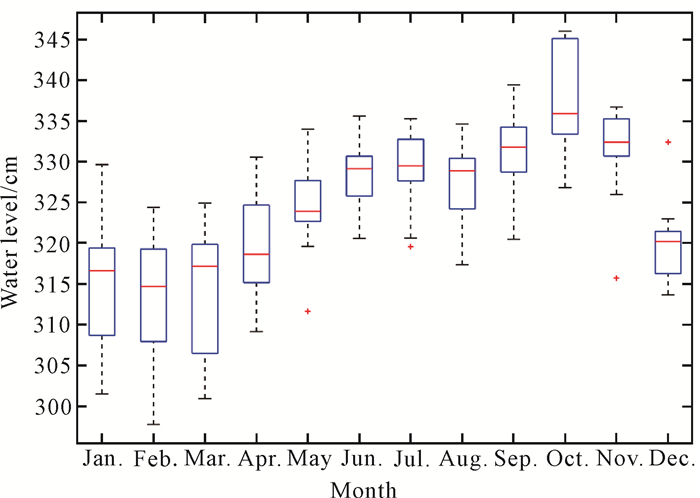
图 5为2008—2020年潮汐月平均水位变化箱形图。其中蓝框上、下界为样本数据的第25个百分位数和第75个百分位数,红线为样本的中位数,上、下限为非离群值的最远端数据值,红十字为离群值。潮水位存在着明显的季节性变化,中位数数值从2-10月逐月增高,在2月份达到最低值(314 cm),10月份达到最高值(336 cm),11月份开始下降。每个月水位变化幅度各不相同,1-2月变化幅度最大,接近30 cm;而12月份的变化幅度最小,约10 cm。影响水位变化的因素有气候、水温、风暴潮等,具体的影响机制还需要进一步研究分析。
|
| 图 5 潮汐月平均水位变化 Fig. 5 Variations of tidal monthly mean water level |
2.3 潮汐不对称性 2.3.1 涨潮和落潮历时统计
为了考察不同分潮对钦州湾潮汐不对称性的影响,将11个分潮分成6种不同的分潮组合,以此来统计2008—2020年的涨潮和落潮平均历时(表 3)。全11个分潮统计结果表明,涨潮平均历时为9.883-10.650 h,落潮平均历时为7.200-7.950 h,平均历时差为2.467-2.967 h,涨潮历时比落潮历时长,存在明显的涨、落潮历时不对称现象,这与李树华[18]研究得出的涨潮历时大于落潮历时、历时差值在2 h以上的结论一致。半日分潮统计结果表明,涨潮平均历时为6.183-6.233 h,落潮平均历时为6.183-6.233 h,涨潮历时和落潮历时大致相同。全日分潮统计结果表明,涨潮平均历时为12.267-12.467 h,落潮平均历时为12.233-12.533 h,涨潮历时和落潮历时大致相同。八大主要分潮统计结果表明,涨潮平均历时为9.833-10.750 h,落潮平均历时为7.150-8.017 h,平均历时差为2.550-2.983 h,涨潮历时均比落潮历时长,存在明显的涨潮和落潮历时不对称的现象,与全11个分潮的统计结果相比,涨潮和落潮平均历时差仅数分钟。
| 分潮 Tidal constituents |
涨潮平均历时/h Mean flood tide duration/h |
落潮平均历时/h Mean ebb tide duration/h |
涨潮和落潮平均历时差/h Mean duration difference of flood tide and ebb tide/h |
| Eleven main tidal constituents | 9.883-10.650 | 7.200-7.950 | 2.467-2.967 |
| Semidiurnal tide (N2,M2,S2,K2) |
6.183-6.233 | 6.183-6.233 | -0.033-0.050 |
| Diurnal tide (Q1,O1,P1,K1) |
12.267-12.467 | 12.233-12.533 | -0.133-0.133 |
| Semidiurnal tide+Shallow water constituent (N2,M2,S2,K2,M4,MS4,M6) |
6.117-6.250 | 6.167-6.317 | -0.200-0.083 |
| Diurnal tide+Shallow water constituent (Q1,O1,P1,K1,M4,MS4,M6) |
12.100-12.350 | 11.600-11.983 | 0.283-0.600 |
| Eight main tidal constituents (Q1,O1,P1,K1,N2,M2,S2,K2) |
9.833-10.750 | 7.150-8.017 | 2.550-2.983 |
上述统计结果显示,在不考虑全日分潮和半日分潮之间的相互作用时,涨潮和落潮历时基本一致,无明显的潮汐不对称性;当考虑全日分潮和半日分潮组合时,存在明显的潮汐不对称现象,故全日分潮和半日分潮之间的相互作用是影响钦州湾涨潮和落潮历时不等的主要原因。在大多数混合潮和日潮的情况下,主要天文分潮(指半日分潮和全日分潮)之间的相互作用普遍存在,会造成潮汐不对称性[24]。
2.3.2 偏度贡献本研究选取的11个分潮可以组合成6组符合上述公式的、能导致潮汐不对称性的特定组合,分别为(K1, K2)、(M2, M4)、(O1, K1, M2)、(P1, K1, S2)、(Q1, K1, N2)、(M2, S2, MS4)。根据分潮的振幅、迟角和频率来计算以上特定组合2008—2020年的偏度(γ)和偏度贡献值(β)(表 4)。
| 组合 Combination |
偏度 γ |
偏度贡献值 β |
| K1, K2 | -0.380 4—-0.301 0 | -0.074 8—-0.060 1 |
| M2, M4 | -0.034 5—0.046 7 | -0.004 4—0.006 9 |
| O1, K1, M2 | -0.638 7—-0.590 6 | -0.566 6—-0.515 3 |
| P1, K1, S2 | -0.182 8—-0.157 3 | -0.0411—-0.035 2 |
| Q1, K1, N2 | -0.107 7—-0.081 2 | -0.021 8—-0.016 7 |
| M2, S2, MS4 | 0.020 6—0.039 4 | 0.003 2—0.006 1 |
| γN | -0.636 5—-0.678 5 |
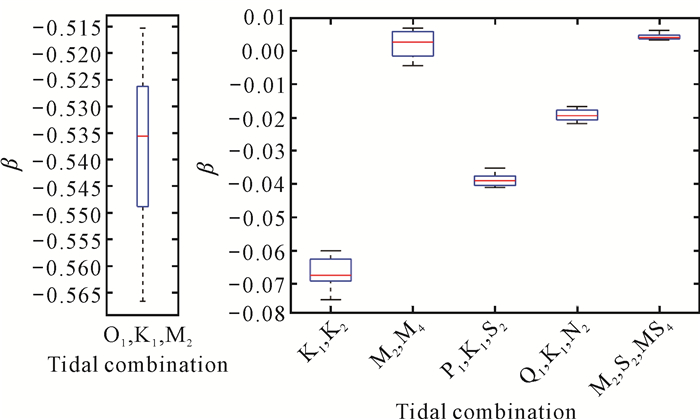
图 6、图 7分别为2008—2020年钦州湾主要分潮组合偏度贡献的年际变化曲线和箱形图。分潮组合β绝对值越大,其对钦州湾潮汐不对称性影响程度越大,且β的正(负)值代表了该分潮组合的涨(落)潮的占优情况。影响钦州湾潮汐不对称性的主要分潮组合分别为(O1, K1, M2)、(K1, K2)、(P1, K1, S2)。其中,(O1, K1, M2)的分潮组合的β绝对值占比较大,为第一贡献组合,其值为负,代表落潮占优,占总潮汐偏度的80.97%-83.51%,与总潮汐偏度有很好的相关性,且该分潮组合在2008—2020年的变化比其他组合范围较大,中位数为-0.535 6。同时,(K1, K2)、(P1, K1, S2)分别作为第二、第三贡献组合,虽然占比略小,但是均为负数,分别占总潮汐偏度的9.36%-11.34%和5.24%-6.46%,与总潮汐偏度的性质一致,即影响钦州湾潮汐不对称性占比前3的特定组合与总潮汐偏度具有较好的相关性,且(K1, K2)、(P1, K1, S2)特定组合在多年间变化幅度较小,具有相对稳定的特点。其余组合的β值大部分都在-0.1至0变化。

|
| 图 6 钦州湾主要分潮组合偏度贡献的年际变化曲线 Fig. 6 Interannual variation curve of the skewness contribution of the main tidal constituent combination in Qinzhou Bay |
|
| 图 7 钦州湾主要分潮组合的偏度贡献箱形图 Fig. 7 Skewness contribution box diagram of main tidal combination in Qinzhou Bay |
值得注意的是,(M2, S2, MS4)组合虽然β绝对值占比非常小,但其值为正,代表涨潮占优。该组合的偏度值与上述统计的半日分潮+浅水分潮的落潮平均历时比涨潮平均历时长的结果一致。
2.4 海平面变化通过对钦州湾2008—2020年的年平均水位进行统计分析,结果发现13年间海平面高度存在一定的年际变化,总体呈上升趋势。利用最小二乘法对海平面高度进行线性拟合,可以得出钦州湾海平面的平均上升速率约为0.96 cm/a (图 8),略低于前人研究分析得出的南海区域整体的海平面年上升速率,如丁荣荣等[25]根据T/P高度基于1992—2002年数据资料对南海区域的香港海域进行分析,得到海平面的平均上升速率为1.21 cm/a;丘福文等[26]根据法国航天局提供的网格化月平均海平面高度距平资料以及英国国家海洋中心的PSMSL资料,得出2005—2010年南海海平面的平均上升速率为1.73 cm/a。中国海平面公报对2008—2020年的南海沿海海平面分析得到该海平面的平均上升速率为0.52 cm/a[27],低于钦州湾海平面的平均上升速率。

|
| 图 8 钦州湾2008—2020年海平面变化趋势 Fig. 8 Trend of sea level in Qinzhou Bay from 2008 to 2020 |
3 结论
本研究通过分析钦州湾验潮站2008—2020年共13年的水位观测数据,结果表明钦州湾的潮型数为4.320-4.654,O1、K1分潮的振幅约是M2分潮的2倍,整体表现为规则全日潮。同时,潮汐具有显著的年际变化特征,三大主要分潮O1、K1和M2的振幅分别为95.82-104.27、88.18-95.15、39.53-46.16 cm,变化幅度为8%-16%,最小值出现在2008年,最大值出现在2016年。钦州湾潮汐不对称性显著,涨潮历时比落潮历时多2-3 h,涨潮流速慢,落潮流速快,这一潮汐特征有利于钦州湾泥沙向外海输运,是钦州湾主要航道长期不淤积的保障。此外,钦州湾海平面呈逐年上升的趋势,平均上升速率约0.96 cm/a,高于同期南海沿海海平面的平均上升速率(0.52 cm/a)。本研究虽然仅分析了一个验潮站13年的潮位序列,但是由于钦州湾海域面积小,潮汐要素区域差异不大,同时观测站位于钦州湾中部,本研究的结果仍具有一定的代表性,可为钦州湾防灾减灾和港口工程建设提供科学依据,在实际近岸工程的设计中应充分考虑潮汐的长期变化特征和海平面上升的影响。
| [1] |
陈波, 侍茂崇, 邱绍芳. 广西主要港湾余流特征及其对物质输运的影响[J]. 海洋湖沼通报, 2003(1): 13-21. |
| [2] |
李树华. 钦州湾潮汐和潮流数值计算[J]. 海洋通报, 1986, 5(4): 27-32. |
| [3] |
孙洪亮, 黄卫民. 广西近海潮汐和海流的观测分析与数值研究: Ⅰ.观测与分析[J]. 黄渤海海洋, 2001, 19(4): 1-11. |
| [4] |
孙洪亮, 黄卫民. 广西近海潮汐和海流的观测分析与数值研究: Ⅱ.数值研究[J]. 黄渤海海洋, 2001, 19(4): 12-21. |
| [5] |
董德信, 李谊纯, 陈宪云, 等. 钦州湾潮流季节变化特征[J]. 广西科学, 2014, 21(4): 351-356. |
| [6] |
张伯虎, 陈沈良, 谷国传. 广西沿岸重点港湾的潮型与潮汐特征[J]. 海洋学研究, 2010, 28(3): 9-16. |
| [7] |
宋德海, 鲍献文, 朱学明. 基于FVCOM的钦州湾三维潮流数值模拟[J]. 热带海洋学报, 2009, 28(2): 7-14. |
| [8] |
赵昌, 吕新刚, 乔方利. 北部湾潮波数值研究[J]. 海洋学报, 2010, 32(4): 1-11. |
| [9] |
NIDZIEKO N J. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides[J]. Journal of Geophysical Research: Oceans, 2010, 115(C8): C08006. |
| [10] |
SONG D H, WANG X H, KISS A E, et al. The contribution to tidal asymmetry by different combinations of tidal constituents[J]. Journal of Geophysical Research, 2011, 116(C12): C12007. DOI:10.1029/2011JC007270 |
| [11] |
李谊纯, 徐群. 瓯江口内外潮汐不对称研究[J]. 水利水运工程学报, 2013(5): 61-65. |
| [12] |
李谊纯, 董德信, 王一兵. 防城港湾潮余流及潮汐不对称特征[J]. 广东海洋大学学报, 2021, 41(4): 50-57. |
| [13] |
李谊纯. 一个潮流不对称计算方法及其在北仑河口的应用[J]. 海洋工程, 2014, 32(4): 110-116. |
| [14] |
李谊纯, 董德信, 赖俊翔, 等. 涠洲岛海域潮流不对称的偏度判别研究[J]. 广西科学, 2014, 21(1): 73-76. |
| [15] |
林国尧, 龚文平. 海南岛莺歌海近岸的潮汐不对称与潮致余流研究[J]. 海洋学报, 2017, 39(7): 36-42. |
| [16] |
童朝锋, 曹益铭, 高祥宇, 等. 海南红塘湾潮汐不对称性分析[J]. 水利水运工程学报, 2019(3): 9-15. |
| [17] |
陈云, 戴志军, 张敏, 等. 长江口新桥水道潮汐不对称性研究[J]. 海洋通报, 2022, 41(5): 528-536. |
| [18] |
李树华. 钦州湾的流况及其水文特征[J]. 海洋湖沼通报, 1988(3): 15-20. |
| [19] |
吕赫, 张少峰, 宋德海, 等. 围填海累积效应对钦州湾水动力环境的影响[J]. 海洋与湖沼, 2021, 52(4): 823-833. |
| [20] |
PAWLOWICZ R, BEARDSLEY B, LENTZ S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J]. Computers & Geosciences, 2002, 28(8): 929-937. |
| [21] |
许秀娥, 张容榕, 韦冬妮. 大连老虎滩海域潮汐调和分析[J]. 海洋预报, 2022, 39(4): 16-23. |
| [22] |
陈宗镛. 潮汐学[M]. 北京: 科学出版社, 1980.
|
| [23] |
金朝辉, 李文龙, 李秀斌, 等. 月球赤纬角与丰满水库来水规律研究[J]. 东北水利水电, 2016, 34(4): 41-42. |
| [24] |
GUO W, SONG D, WANG X H, et al. Contributions of different tidal interactions to fortnightly variation in tidal duration asymmetry[J]. Journal of Geophysical Research: Oceans, 2016, 121(8): 5980-5994. DOI:10.1002/2016JC011689 |
| [25] |
丁荣荣, 左军成, 杜凌, 等. 南海海平面变化及其比容高度和风场间的关系[J]. 中国海洋大学学报(自然科学版), 2007, 37(S2): 23-30. |
| [26] |
丘福文, 方文东, 朱大勇, 等. 2005—2010年南海海平面异常升高的特征与机制[J]. 热带海洋学报, 2015, 34(5): 11-18. |
| [27] |
自然资源部海洋预警监测司. 2020年中国海平面公报[EB/OL]. (2021-04-26)[2023-04-04]. http://gi.mnr.gov.cn/202104/t20210426_2630186.html.
|



