随着云计算和物联网等新技术的飞速发展,数据流分类算法被应用于许多领域,如信用卡欺诈检测、交通监控和医疗决策辅助等。数据流中数据的分布可能随时间、环境的变化而改变,这种变化被称为概念漂移[1]。概念漂移问题给机器学习带来了巨大的挑战,在存在概念漂移的数据流分类任务中,如果模型不能尽早识别新概念且动态地调整分类器,则模型分类准确率会迅速下降。数据流分类问题中,在新概念出现的初期仅能获取到少量样本,用这些少量样本训练出的模型分类效果较差,但是基于数据流分类中不同概念之间的数据依然存在可学习性[2]这一共识,故用迁移学习来提升数据流分类的性能就成目前研究的热点[3]。
迁移学习根据源领域的数量可以分为单源迁移学习和多源迁移学习[4]。单源迁移学习源领域数量单一,存在信息不充分的问题。多源迁移学习能够有效地利用来自不同分布的相关源领域的知识来提高目标领域分类任务的性能[5]。例如,Eaton等[6]提出TransferBoost算法,该算法合并多个源领域与目标领域的样本,并根据样本的迁移能力为各源领域的每个样本设置权重。Chattopadhyay等[7]基于源领域和目标领域的样本分布具有相似性这一特点,提出CP-MDA算法。Gao等[8]提出LWE算法,该算法在每个源领域上分别训练一个组件分类器,并对每个组件分类器赋予不同的权值,然后根据权值加权集成。Ge等[9]提出OMS-TL算法,该算法将离线的MSTL算法改进为在线算法。Wu等[10]提出的OTLMS算法根据每个源领域分类器对目标领域样本的分类准确度为每个源领域分类器设置一个权重,并根据分类性能自适应调节权重大小。Kang等[11]提出适用于多分类任务的OMTL-MC算法,OMTL-MC算法采用两段集成的思想,从多个源领域迁移知识来辅助目标领域的学习任务。文益民等[12]提出RCOTL算法,该算法通过计算拟分类样本与分类器池中各个分类器之间的领域相似度,改善了从源领域到目标领域的知识迁移,解决了重现概念数据流分类中的“概念漂移检测滞后”和“负迁移”的问题。秦一休等[13]针对CDOL算法的不足,提出CMOL算法,该算法使用将权重最大的分类器从分类器池中替换出去的策略,保证了分类器池中的分类器多样性最大化。Sun等[14]提出DTEL集成模型,该算法利用源领域中所包含的知识实现概念漂移自适应训练。吕艳霞等[15]在DTEL集成模型的基础上,基于准确率调整范围参数的模型更新策略提出了HAEL集成框架,该算法引入注意力机制,使其更倾向于使用目标领域样本构建和更新分类模型。Zhao等[16]采用最小二乘支持向量机作为组件分类器,提出了Condor SVM算法,该算法采用偏差正则化技术以利用源领域的分类器来进行迁移学习,并根据源领域分类器对目标样本的分类性能来调整各源领域分类器的权重。赵鹏等[17]采用决策树作为组件分类器,提出了Condor Forest算法,该算法采用乘法权重更新法来更新模型库中每个模型的权重,并挑选权重最大的模型作为可重复使用的模型。然而,上述多源迁移学习算法在源领域与目标领域相似度低时,迁移效果不好。唐诗淇等[18]针对这个问题,提出了一种基于局部分类精度的多源在线迁移学习算法LC-MSOTL,LC-MSOTL维护一个源领域分类器池,通过计算局部分类精度,从源领域分类器池中挑选出一个分类器来提升目标领域的分类性能。但是,在动态数据流环境中,LC-MSOTL由于缺少分类器池更新机制以及所用的最近邻算法对拟分类样本周围邻居查找不够准确等原因,其分类效果并不理想。
针对这些问题,本文提出了一种基于局部分类精度的概念漂移数据流分类算法——LA-MS-CDC,LA-MS-CDC基于多源在线迁移学习框架,能有效适应概念漂移数据流环境,并且较好地解决了LC-MSOTL算法存在的问题。具体来说,基于支持向量差异性最大化提出的一种维护分类器池多样性最大化的方法保证了分类器池中的分类器尽可能多地映射不同概念,提高了算法对概念漂移的处理能力;根据源领域和目标领域动态权重比提出的一种选择性更新源领域分类器的方法有效避免了负迁移的发生。
1 LA-MS-CDC样本以在线的方式到来并进行分类,本文设定xi为在第i时刻到达的样本:(xi, yi)∈X×Y,X∈Rn,Y={-1,+1},X为n维的属性空间,Y为样本的标记空间,yi为样本的标记值。
LA-MS-CDC的流程如算法1所示,其基于多源在线迁移学习进行数据流分类。为了应对数据流环境中的数据分布变化,LA-MS-CDC周期性对分类器池进行更新。在开始阶段,使用初始数据样本训练一个源领域分类器fs,初始化分类器池CF、k-means聚类簇心、源领域权重α1,1、目标领域分类器权重α2,1及目标域分类器ft(行1-6),各在线分类器均为Passive Aggressive (PA)[19]分类器。
针对每一个样本xi,以在线学习的方式进行如下操作:首先找到xi所属聚类簇的簇心cmin,并且使用样本xi更新k-means聚类簇心(行8-9);其次使用Select函数从分类器池中挑选出一个最优源领域分类器fsk,与目标领域分类器ft加权集成后,对样本xi进行预测(行10-11),当分类任务结束后,获得样本xi的真实标签yi,更新源领域权重α1,i、目标领域权重α2,i与目标领域分类器ft(行12-13),如果源领域权重与目标领域权重比值大于指定的阈值θ,则更新最优源领域分类器fsk(行14-16);最后将样本(xi,yi)存入数据缓存器BD中(行17)。当数据缓存器BD中的样本达到容量上限后,将目标领域分类器加入分类器池中,完成分类器池的更新操作(行18-22)。同时,再次初始化源领域权重α1,i+1、目标领域权重α2,i+1、数据缓存区BD、目标领域分类器ft(行23-25)。
算法1 LA-MS-CDC
输入: 流数据{(xi, yi),…,(xT, yT)}分类器池大小M,数据缓存器BD的大小N,近邻个数K,放大系数ζ,聚类簇数n,源领域与目标领域权重阈值θ。
输出: xi的预测标签yi。
1.利用开始的数据训练一个PA分类器fs1
2.初始化分类器池CF={fs1}
3.利用开始的数据初始化聚类簇心列表(c1, c2, …, cn)
4.α1,1=0.5,α2,1=0.5
5.ft=create() /*create()函数为初始化目标域分类器*/
6.BD=[]
7.for i=1 to T do
8. 获得xi所属簇的簇心cmin
9. (c1, c2, …, cn)=update_cluster(xi(c1, c2, …, cn)) /*update_cluster()函数为更新聚类簇心函数*/
10. fsk=Select(CF, BD, xi, K, ζ, cmin, (c1, c2, …, cn))
11.
12.
13. ft update(xi, yi)/*update( )函数为更新目标域分类器*/
14. if α1,i+1/α2,i+1>θ
15. fsk.update(xi, yi) /*更新源领域分类器*/
16. end if
17. BD.save(xi, yi)
18. if |BD|=N
19. CF.add(ft)/*将训练好的目标域分类器加入分类器池*/
20. if |CF|>M
21. 从CF中删除支持向量差异性最小的分类器
22. end if
23. α1, i+1=0.5, α2, i+1=0.5
24. ft=create()
25. BD=[]
26. end if
27.end for
28.return
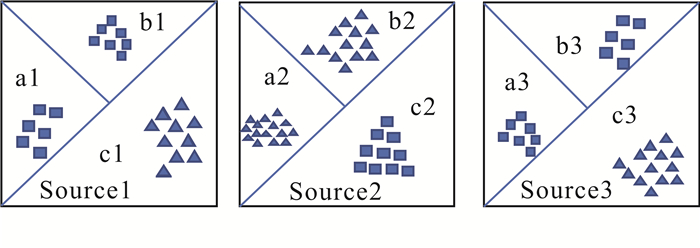
1.1 基于k-means聚类的局部分类精度的算法Gao等[8]注意到源领域与目标领域有相似的局部流形,每个源领域与目标领域都有较大的不同,但又都各自存在分布相同的局部。若在每个源领域上训练一个分类器,并把这些分类器迁移到目标域上辅助目标领域进行分类,必然会产生“负迁移”。如图 1所示,目标领域a3区域与源领域b1区域分布相同,与b2区域分布相异,若使用b1训练的分类器对a3区域数据进行分类,样本就会被正确分类; 若使用b2区域训练的分类器对a3区域进行分类,样本就会被错误分类。因此,对于目标领域中的样本,若能为每个样本选择合适的源领域分类器对其进行辅助分类,就能更好地实现知识迁移,从而对目标领域样本更准确地分类。
|
| 图 1 源领域与目标领域的局部相似性 Fig. 1 Local similarity between source domain and target domain |
局部分类精度是分类器选择中的一种有效方法[8, 20-22]。由于每个组件分类器对拟分类样本的邻域分类能力不同,因此该方法选择局部分类精度最高的源领域分类器为最优源领域分类器,其中训练该最优源领域分类器的数据与拟分类样本的邻域相似度最高。第j个组件分类器fsj针对拟分类样本xi的局部分类精度LCj的计算方法如公式(1)所示。
| $L C_j=\sum\limits_{m=1}^k \frac{I\left(f_{s_j}\left(x_m\right)=y_m\right)}{e^{\xi \operatorname{dis}\left(x_i, x_m\right)}}, $ | (1) |
其中,xi为拟分类样本的特征向量,k为其邻域的样本数量,(xm, ym)为该邻域中第m个样本的特征向量和真实类别,样本(xm, ym)来自数据缓存器BD,dis(xi, xm)为样本xm与拟分类样本xi的欧式距离,ζ为放大系数,I(x)为指示函数,其形式如公式(2)所示:
| $I(x)=\left\{\begin{array}{ll}1, & x=\text { true} \\ 0, & x=\text { false}\end{array}\right. 。$ | (2) |
LC-MSOTL算法[18]使用K近邻算法挑选距离拟分类样本最近的K个样本作为邻居,然而,LC-MSOTL算法在带有概念漂移的数据流环境中所找到的邻居样本并不准确,具体表现为分类器池中的各个分类器在局部邻域上计算出的局部分类精度很小甚至为零,这说明通过K近邻算法找到的拟分类样本的邻居样本有误,从而导致根据局部分类精度挑选出来的源领域分类器对拟分类样本的分类辅助能力很弱。
LA-MS-CDC针对LC-MSOTL算法无法准确找出待分类样本的邻居样本这一问题做出改进,使用k-means聚类算法保留已分类数据的聚类簇信息。k-means聚类算法是一种经典的聚类算法,其思想简单,聚类效果良好,应用广泛。相比于其他聚类算法,k-means聚类算法具有计算速度快,资源消耗少,并且适用于在线学习环境等优点。使用k-means聚类算法改进后,每当一个新样本到来时,首先查找该新样本所属的簇,其次使用该新样本更新簇心信息,最后使用K近邻算法在该簇上寻找新样本的K个邻居。
动态挑选源领域分类器的Select函数伪代码如算法2所示。首先,新建一个空列表sameList(行1),其次在数据缓存器BD中寻找与拟分类样本在同一簇的样本,并将这些样本与待分类样本间的欧式距离存入sameList中(行2-7),再从sameList中寻找拟分类样本xi的K个邻居(行10-14),最后根据局部分类精度计算公式从分类器池CF中挑选出最优源领域分类器fsk(行15)。若找不到最优源领域分类器fsk,分类器池中的各个分类器均对xi预测标签,依据多数类投票原则确定xi的标签为ys,再从预测为ys的分类器中随机挑选一个分类器作为fsk(行16-18)。
算法2 Select函数
输入: 聚类簇心c1,c2,…,cn新到样本特征向量xi,xi所属簇的簇心cmin,分类器集合CF,数据缓存器BD,近邻个数K,放大系数ζ。
输出: 最优源领域分类器fsk。
1.sameList=[]
2.for j=1 to |BD| do
3. if min_cluster(xj,(c1,c2,…,cn))=cmin do /*函数min_cluster()为样本xj距离最近的簇心*/
4. disj=dis(xi,xj)
5. sameList.add(disj)
6. end if
7.end for
8.sort(sameList)
9.Kneighbor=[]
10.for n=1 to |sameList| do
11. 根据sameList[n]找到对应的邻居样本(xn,yn)
12. Kneighbor.add((xn,yn))
13. if (n≥K) break
14.end for
15.
16.if fsk=Ø
17. CF中所有分类器按照多数类投票决定xi的标签ys
18. 从预测为ys的分类器中随机挑选一个分类器作为fsk
19.return fsk
1.2 LA-MS-CDC的更新机制 1.2.1 源领域分类器选择性增量更新增量学习是指使用不断接收的新数据持续地调整和更新模型,增量学习可以在保留大部分过去有效知识的情况下学习新知识。当概念漂移现象出现在增量学习中时,如果不针对性地调整模型的增量更新机制,新到的概念往往与模型中已经学习到的概念相冲突并影响学习的效果[23]。
LA-MS-CDC为解决在概念漂移环境下新到数据知识与模型中已有知识相冲突的问题,当源领域权重与目标领域权重比值大于阈值θ时,增量更新最优源领域分类器。当θ很小时,说明源领域分类器对拟分类样本的分类结果贡献度低,此时的源领域分类器对拟分类样本的分类错误率较高,即源领域分类器学到的知识与当前拟分类样本的信息相冲突。因此用拟分类样本增量更新最优源领域分类器并不合理,反之亦然。
1.2.2 目标领域分类器的更新策略目标领域分类器为在线学习器PA,当得到样本xi的预测标签后,则用样本xi的预测标签和真实标签更新目标领域分类器,具体步骤如下:
① 使用hinge-loss损失函数计算分类器损失lt;
② 若lt>0,则对分类器进行更新wt+1=wt+τytxt,其中τ=min(C,lt/‖xt‖2)。
1.2.3 权重α1,i和α2,i的更新策略源领域权重α1,i和目标领域权重α2,i的更新机制:在算法开始时初始化为0.5,每分类完一个样本则按照公式(3)和公式(4)更新[24]。
| $\alpha_{1, i+1}=\frac{\alpha_{1, i} s_i\left(w_s\right)}{\alpha_{1, i} s_i\left(w_s\right)+\alpha_{2, i} s_i\left(w_t\right)}, $ | (3) |
| $\alpha_{2, i+1}=\frac{\alpha_{2, i} s_i\left(w_t\right)}{\alpha_{1, i} s_i\left(w_s\right)+\alpha_{2, i} s_i\left(w_t\right)}, $ | (4) |
其中,
集成学习能够提高组件分类器的泛化能力[25, 26],然而当各个组件分类器的表现都相同时,集成分类器的分类性能将不会提高,因此多样的组件分类器往往可以提高集成学习的性能。在数据流场景下,分类器池多样性最大化的具体表现为在分类器池中最大限度地映射多种概念,保留尽可能多的过去有效信息。目前多样性的度量方法主要分为非成对度量和成对度量[27],因LA-MS-CDC算法所采用的组件分类器为在线学习分类器PA,故本文结合组件分类器自身的特性提出了一种度量分类器池多样性的新指标,即依据支持向量差异性最大化来维护分类器池多样性最大化。
PA分类器是一种基于感知机的在线学习分类器,它利用支持向量维护分类决策面,进而实现对样本的分类。因此,分类器池中各种分类器可以用支持向量来具体化。当分类器池中的支持向量的差异性最大时,也就说明了分类器池存储的分类决策面差异性最大,即分类器池中的分类器多样性最大。
假设LA-MS-CDC维护的分类器池已满。当目标领域分类器ft训练完成后,第一步,将ft加入分类器池中;第二步,依次删除分类器池中的一个分类器,分别计算任意两个不同组件分类器中支持向量相同的个数,并累积求和。当删除分类器池中某个分类器fi后累积的支持向量个数最小时,说明分类器池多样性最大,此时fi为分类器池本轮应该删除的分类器。本文采用的多样性度量方法为成对度量,fi的求解如公式(5)所示。
| $f_i=\underset{\left(C F-f_i\right)}{\operatorname{argmin}} \sum\limits_{m=1}^M \sum\limits_{n=m+1}^M \operatorname{sum}\left(v_m=v_n\right), $ | (5) |
其中,M为分类器池CF的容量,sum(vm=vn)表示分类器fm与分类器fn中支持向量相同的数量。
2 实验及结果分析 2.1 数据集和实验设置本文采用Letter数据集和waveform数据集来测试LA-MS-CDC的性能。Letter数据集是来自加利福尼亚大学尔湾分校(UCI)的真实数据集,该数据集共计20 000个样本,包含16维连续属性和26种类别,这26种类别分别对应26个字母。waveform数据集是人工数据集,来自数据流领域常用的开源学习框架MOA[28]。
本文使用Letter数据集制作ABCD数据集、EFGH数据集、NOPQ数据集。由于原始的Letter数据集中并未包含概念漂移,为了更有效地对LA-MS-CDC算法的性能进行测试,将Letter数据集按照表 1方式标注正、负类类别标签,并以此来产生概念漂移,共生成3种概念,ABCD数据集的第1-400个样本组成概念A,数据集的第401-800个样本组成概念B,数据集的第801-1 200个样本组成概念C,其中概念A到概念B为突变概念,EFGH数据集和NOPQ数据集生成概念漂移的方式与ABCD数据集相同。
| 字母集 Letter set |
概念A Concept A 1-400 |
概念B Concept B 401-800 |
概念C Concept C 801-1 200 |
| A(E)(N) | - | + | + |
| B(F)(O) | - | + | - |
| C(G)(P) | + | - | + |
| D(H)(Q) | + | - | - |
waveform原始数据集共计5 500个样本,包含21个连续属性和3个类别。为使waveform数据集包含概念漂移,将waveform数据集按照表 2所示的方式标注正、负类类别标签,共生成3种概念,每种概念重复2次,共产生9个概念。其中,数据集的第1-600个样本组成概念E,数据集的第601-1 200个样本组成概念F,数据集的第1 201-1 800个样本组成概念G。
| 原始类别 Original category |
概念E Concept E 1-600 |
概念F Concept F 601-1 200 |
概念G Concept G 1 201-1 800 |
| 1 | - | + | - |
| 2 | + | - | - |
| 3 | + | + | + |
将采用表 1和表 2的方式处理的数据集作为实验数据集,可以帮助证明LA-MS-CDC算法具有挖掘出源领域和目标领域的局部相似性的能力。基于这种局部相似性,LA-MS-CDC能挑选出最合适的源领域分类器,从而进行更有效的迁移学习。如表 1所示,概念A与概念C中的B类别均打上了负标签,如果能挖掘出概念A和概念C所具有的这种局部相似性,就可以从分类器池中挑选由概念A训练的分类器fa,从而实现对概念C中的B类别正确分类。同理,概念B与概念C中的A类别均打上了正标签,如果能从分类器池中挑选由概念B训练的分类器fb,则可以对概念C中的A类别正确分类。
本文实验在3.6 GHz Intel Core i5-7700的CPU、16 GB RAM的Windows 7计算机上进行。
2.2 实验结果分析 2.2.1 算法的有效性为了评估LA-MS-CDC在多源在线迁移学习中的迁移学习能力,本文选择了两种多源在线迁移学习算法OTLMS算法[10]、LC-MSOTL算法[18]以及一种在线学习算法PA[19]作为对比算法。其中,PA算法直接在线学习目标领域样本;LA-MS-CDC算法、OTLMS算法、LC-MSOTL算法的实验方案为预先训练2个源领域分类器,然后再学习目标领域样本。
为了验证LA-MS-CDC算法在概念漂移数据流算法中的优越性,本文选择Condor SVM算法[16]作为对比算法。Condor SVM算法能自适应挖掘历史数据中对当前预测有用的知识,是目前性能较优秀的概念漂移数据流算法之一。
LC-MS-CDC算法在多源迁移学习和概念漂移数据流分类问题中的有效性实验结果见表 3。为了减弱数据流中样本出现次序的随机性对实验结果的影响,在每次实验前,每份实验数据随机打乱顺序,共打乱顺序10次,最终结果为10次实验结果的平均值,并且对表 3的实验结果进行算法稳定性检验和累计准确率显著性差异分析。使用累计准确率的标准差表示各算法的稳定性,使用95%置信水平下的成对t检验分析LA-MS-CDC算法和基线方法的分类性能是否存在显著性差异。
| Unit: % | |||||||||||||||||||||||||||||
| 数据集 Dataset |
迁移学习 Transfer learning |
概念漂移 Concept drift |
|||||||||||||||||||||||||||
| PA[19] | OTLMS[10] | LC-MSOTL[18] | LA-MS-CDC | Condor SVM[16] | LA-MS-CDC | ||||||||||||||||||||||||
| ABCD | 68.31±0.01■ | 69.42±0.01■ | 88.74±0.05■ | 92.52±0.12 | 87.13±0.01■ | 88.02±0.01 | |||||||||||||||||||||||
| EFGH | 65.43±0.01■ | 66.95±0.01■ | 84.11±0.01□ | 88.64±0.02 | 84.27±0.01□ | 84.36±0.02 | |||||||||||||||||||||||
| NOPQ | 63.87±0.01■ | 65.75±0.01■ | 84.51±0.07■ | 94.88±0.11 | 86.24±0.01■ | 87.02±0.01 | |||||||||||||||||||||||
| waveform | 77.89±0.01■ | 79.03±0.01■ | 88.38±0.02■ | 95.56±0.10 | 80.73±0.01■ | 85.68±0.01 | |||||||||||||||||||||||
| Note: bold represents the result of LC-MS-CDC.■represents LA-MS-CDC significantly better than the baseline method (P<0.05);□represents LA-MS-CDC significantly worse than the baseline method (P<0.05). | |||||||||||||||||||||||||||||
表 3的“迁移学习”部分验证了LA-MS-CDC算法的迁移学习效果,“概念漂移”部分验证了LA-MS-CDC算法在概念漂移数据流环境中的学习性能。实验结果表明,LA-MS-CDC算法在分类效果上优于迁移学习领域的基线方法和数据流领域的基线方法,并且在分类准确率上显著优于对比算法,这是LA-MS-CDC算法中选择性增量更新策略、分类器池多样性最大化策略以及局部分类精度策略共同作用的结果。
2.2.2 选择性增量更新策略的有效性为了验证LA-MS-CDC算法增量更新的有效性,本文在Letter数据集、waveform数据集上对比了3种源领域分类器增量更新方法:选择性增量更新源领域分类器(update)、不增量更新源领域分类器(no-update)、无限制增量更新源领域分类器(no_limit_update)。3种源领域增量更新方法在Letter数据集、waveform数据集上的有效性见图 2。选择性增量更新源领域分类器(update)的分类效果最佳。update的分类效果都优于no-update的分类效果。

|
| 图 2 增量更新有效性对比 Fig. 2 Comparison of incremental update effectiveness |
选择性增量更新源领域分类器(update)与无限制增量更新源领域分类器(no_limit_update)的实验结果说明,LA-MS-CDC算法的选择性更新策略能有效减少增量学习中因学习的知识冲突而影响分类效果的情况。
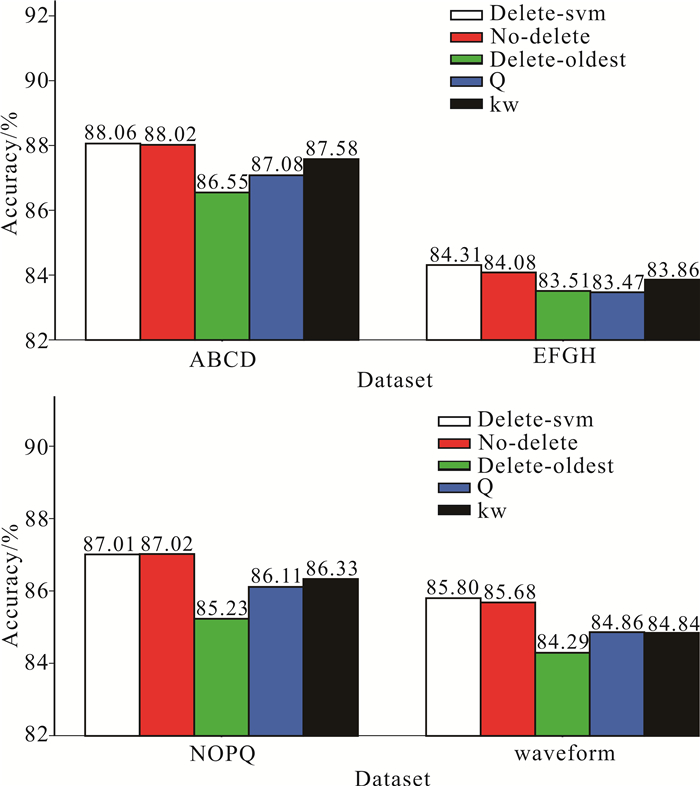
2.2.3 维护分类器池多样性最大化更新策略的有效性为了综合评估LA-MS-CDC算法在维护分类器池多样性最大化的有效性,本文设置5种分类器池更新策略:No-delete,不限制分类器池大小;Delete-oldest,限制分类器池大小,删除最老分类器;Delete-svm,限制分类器池大小,并依据支持向量差异性最大化删除分类器;Q,限制分类器池大小,并依据Q统计维护分类器池多样性最大化;kw,限制分类器池大小,并依据多样性度量Kohavi-Wolpert方差维护分类器池多样性最大化。其中,第4种分类器池更新策略为成对多样性度量中的经典方法,第5种分类器池更新策略为非成对多样性度量中的经典方法,实验结果见图 3。使用支持向量差异性维护分类器池多样性最大化,能够得到与分类器池无限大相近的实验结果,这说明分类器池中的各分类器确实存在冗余,并且本文提出的分类器池更新策略可以最大限度地保留对后续分类任务有帮助的分类器。对比删除最老分类器的分类器池更新策略,Delete-svm策略明显具有优越性。
|
| 图 3 不同分类器池更新算法分类准确率对比 Fig. 3 Comparison of classification accuracy of different classifier pool update algorithms |
2.2.4 基于k-means聚类的局部分类精度算法的有效性
k-means聚类算法与局部分类精度算法相结合,能把过去的有效数据信息保存为簇信息,将簇信息与当前样本的信息相结合,进而实现了查找邻居的准确性。为证明基于k-means聚类的局部分类精度算法能更准确地查找拟分类样本的邻居样本,在ABCD数据集上设计对照实验。实验分为两组,一组采用基于k-means聚类的局部分类精度算法,一组采用LC-MSOTL算法中的局部分类精度算法。为了区分样本,按照样本的到来顺序给样本编号,例如待分类样本编号523,即为第523个到来的样本,通过列举4个拟分类样本在这两种实验方案中所查找到的邻居样本编号,以及邻居样本与拟分类样本是否属于同一概念,来验证LA-MS-CDC算法的有效性。
由表 4可知,对于523号样本,使用基于k-means的局部分类精度算法找到的邻居样本为471、392、422和495号样本。其中,与523号样本属于同一概念的样本是471、422和495号样本,与523号样本属于不同概念的有392号样本。对比LC-MSOTL算法的局部分类精度算法,该算法找到的邻居样本中的392、379号样本与待分类样本(编号523)属于不同概念,不同概念邻居样本的数量将影响局部分类精度计算的准确性[式(1)]。同时,采用基于k-means的局部分类精度的实验组在ABCD数据集上的分类准确率为8876%,采用LC-MSOTL算法的局部分类精度的实验组在ABCD数据集上的分类准确率为87.05%。因此,在查找拟分类样本的邻居时,基于k-means聚类的局部分类精度算法与LC-MSOTL算法的局部分类精度算法相比,能通过簇心保存更多有效的历史数据信息,从而更准确地查找到拟分类样本的邻居样本,进而提高分类准确率。
| 待分类样本编号 Number of samples to be classified |
基于k-means的局部分类精度 Local classification accuracy based on k-means |
LC-MSOTL算法的局部分类精度 Local classification accuracy based on LC-MSOTL |
|||||
| 邻居样本编号Neighbor number | 同概念样本编号Same concept number | 不同概念样本编号Different concept number | 邻居样本编号Neighbor number | 同概念样本编号Same concept number | 不同概念样本编号Different concept number | ||
| 523 | 471,392,422,495 | 471,422,495 | 392 | 471,392,422,495,379 | 471,422,495 | 392,379 | |
| 567 | 522,387,507,511 | 522,507,511 | 387 | 522,387,507,361,511 | 522,507,511 | 387,361 | |
| 2953 | 2938,2910,2837 | 2938,2910,2837 | None | 2938,2910,2823,2756,2837 | 2938,2910,2823,2837 | 2756 | |
| 2997 | 2885,2882,2780 | 2885,2882 | 2780 | 2763,2771,2885,2822,2780 | 2885,2822 | 2763,2771,2780 | |
| Accumulated accuracy | 88.76% | 87.05% | |||||
2.2.5 参数敏感性分析
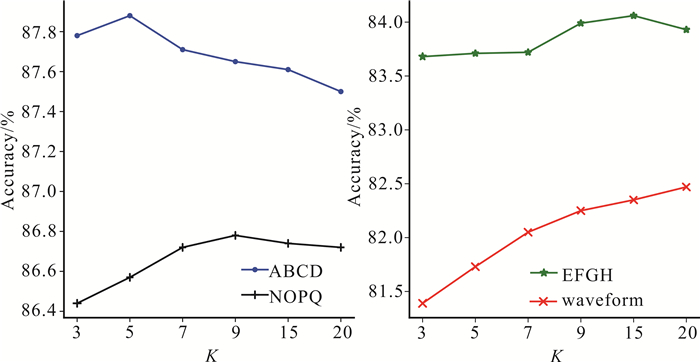
为了验证组件分类器的最近邻数K、源领域与目标领域的权重比值θ对算法的影响,本文设置不同的参数值,分析各参数对LA-MS-CDC算法分类准确率的影响。关于最近邻数K、源领域与目标领域权重比值θ的敏感性实验结果分别见图 4、图 5。
|
| 图 4 不同数据集上最近邻数K对分类准确率的影响 Fig. 4 Influence of nearest neighbor K on classification accuracy on different datasets |
|
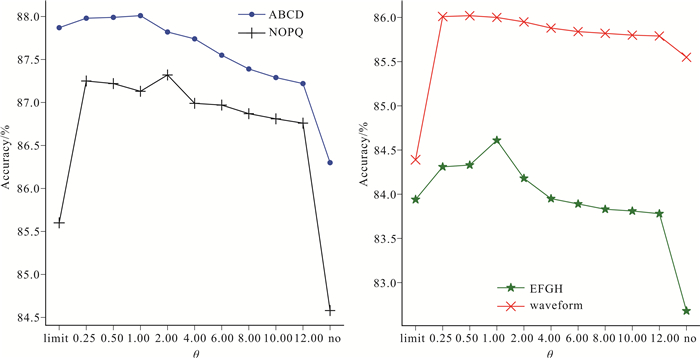
| 图 5 源领域与目标领域权重比值θ对分类准确率的影响 Fig. 5 Influence of the weight ratio θ between source domain and target domain on classification accuracy |
实验结果表明最近邻数K、源领域与目标领域权重比值θ在不同的数据集上有不同的取值,取值的差异性由数据集本身的特性决定。分类准确率的波峰所对应的参数值,就是该数据集下的最优参数值。在参数θ的敏感性分析中,横坐标limit代表无限制增量更新源领域分类器,no代表不增量更新源领域分类器横坐标从左向右表示增量更新源领域分类器的条件越来越严格。更新源领域分类器的严格程度与数据集中概念的相似度有关。由图 5可知,分类准确率随着增量更新条件的严苛程度而逐渐降低,这说明了增量更新源领域分类器能使得源领域分类器获得更好的学习效果,进而提高分类准确率。
3 结论本文提出一种新型的基于局部分类精度的多源在线迁移学习算法LA-MS-CDC,用于概念漂移数据流分类。LA-MS-CDC算法首先将k-means聚类算法与局部分类精度算法相结合,通过提取过去的有效信息,更准确地查找到拟分类样本的邻居样本,解决了LC-MSOTL算法最近邻居查找不准确的问题。为进一步应对概念漂移数据流场景,LA-MS-CDC算法使用支持向量差异性最大化维护分类器池多样性最大化,使得分类器池最大限度地映射多种概念,并用实验证明了这种多样性指标的有效性。同时,为降低增量学习中因学习的知识相冲突造成分类性能变差的问题,LA-MS-CDC算法依据源领域与目标领域的权重比值,选择性增量更新最优源领域分类器,实验说明这种增量更新机制的有效性。在未来的工作中,挖掘源领域和目标领域的局部相似性,并将有效的源领域知识迁移到目标域上还有待进一步研究。
| [1] |
文益民, 刘帅, 缪裕青, 等. 概念漂移数据流半监督分类综述[J]. 软件学报, 2022, 33(4): 1287-1314. |
| [2] |
LIN Y H, CHANG L. An online transfer learning framework for time-varying distribution data prediction[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 6278-6287. DOI:10.1109/TIE.2021.3090701 |
| [3] |
ZHUANG F Z, QI Z Y, DUAN K Y, et al. A comprehensive survey on transfer learning[J]. Proceedings of the IEEE, 2021, 109(1): 43-76. DOI:10.1109/JPROC.2020.3004555 |
| [4] |
庄福振, 罗平, 何清, 等. 迁移学习研究进展[J]. 软件学报, 2015, 26(1): 26-39. |
| [5] |
NGUYEN C V, LE K H, TRAN A M, et al. Learning for amalgamation: a multi-source transfer learning framework for sentiment classification[J]. Information Sciences, 2022, 590: 1-14. DOI:10.1016/j.ins.2021.12.059 |
| [6] |
EATON E, DESJARDINS M. Selective transfer between learning tasks using task-based boosting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2011, 25(1): 337-343. DOI:10.1609/aaai.v25i1.7932 |
| [7] |
CHATTOPADHYAY R, YE J P, PANCHANATHAN S, et al. Multi-source domain adaptation and its application to early detection of fatigue[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM, 2011: 717-725.
|
| [8] |
GAO J, FAN W, JIANG J, et al. Knowledge transfer via multiple model local structure mapping[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas: ACM, 2008: 283-291.
|
| [9] |
GE L, GAO J, ZHANG A D. OMS-TL: a framework of online multiple source transfer learning[C]//Proceedings of the 22nd ACM International Conference on Information and Knowledge Management. San Francisco: ACM, 2013: 2423-2428.
|
| [10] |
WU Q Y, ZHOU X M, YAN Y G, et al. Online transfer learning by leveraging multiple source domains[J]. Knowledge and Information Systems, 2017, 52(3): 687-707. DOI:10.1007/s10115-016-1021-1 |
| [11] |
KANG Z, YANG B, YANG S, et al. Online transfer learning with multiple source domains for multi-class classification[J]. Knowledge-Based Systems, 2020, 190: 105149. DOI:10.1016/j.knosys.2019.105149 |
| [12] |
文益民, 唐诗淇, 冯超, 等. 基于在线迁移学习的重现概念漂移数据流分类[J]. 计算机研究与发展, 2016, 53(8): 1781-1791. |
| [13] |
秦一休, 文益民, 何倩. 概念漂移数据流分类中的多源在线迁移学习算法[J]. 计算机科学, 2019, 46(1): 64-72. |
| [14] |
SUN Y, TANG K, ZHU Z X, et al. Concept drift adaptation by exploiting historical knowledge[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4822-4832. DOI:10.1109/TNNLS.2017.2775225 |
| [15] |
吕艳霞, 刘波男, 王翠荣, 等. 面向概念漂移数据流的自适应增量集成分类算法[J]. 小型微型计算机系统, 2019, 40(12): 2624-2630. DOI:10.3969/j.issn.1000-1220.2019.12.028 |
| [16] |
ZHAO P, CAI L W, ZHOU Z H. Handling concept drift via model reuse[J]. Machine Learning, 2020, 109: 533-568. DOI:10.1007/s10994-019-05835-w |
| [17] |
赵鹏, 周志华. 基于决策树模型重用的分布变化流数据学习[J]. 中国科学: 信息科学, 2021, 51(1): 1-12. |
| [18] |
唐诗淇, 文益民, 秦一休. 一种基于局部分类精度的多源在线迁移学习算法[J]. 软件学报, 2017, 28(11): 2940-2960. |
| [19] |
CRAMMER K, DEKEL O, KESHET J, et al. Online passive-aggressive algorithms[J]. Journal of Machine Learning Research, 2006, 7: 551-585. |
| [20] |
ZHOU Z H, LI M. Semi-supervised regression with co-training[C]//Proceedings of the 19th International Joint Conference on Artificial Intelligence. NewYork: ACM, 2005: 908-913.
|
| [21] |
ZHOU Z H, LI M. Semi-supervised regression with cotraining-style algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(11): 1479-1493. DOI:10.1109/TKDE.2007.190644 |
| [22] |
WOODS K, KEGELMEYER W P, BOWYER K. Combination of multiple classifiers using local accuracy estimates[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(4): 405-410. DOI:10.1109/34.588027 |
| [23] |
熊旺. 数据流增量学习关键技术研究[D]. 长沙: 国防科技大学, 2018.
|
| [24] |
ZHAO P L, HOI S C H. OTL: a framework of online transfer learning[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa: Omnipress, 2010: 1231-1238.
|
| [25] |
HANSEN L K, SALAMON P. Neural network ensembles[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(10): 993-1001. DOI:10.1109/34.58871 |
| [26] |
DIETTERICH T G. Ensemble learning[M]. Cambridge: The MIT Press, 2002.
|
| [27] |
KUNCHEVA L I, WHITAKER C J. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy[J]. Machine Learning, 2003, 51: 181-207. |
| [28] |
ALBERT B, GEOFF H, RICHARD K, et al. MOA: massive online analysis[J]. Journal of Machine Learning Research, 2010, 11: 1601-1604. |



