2. 南宁学院信息工程学院, 广西南宁 530200;
3. 广西医科大学基础医学院, 广西南宁 530021
2. School of Information Engineering, Nanning University, Nanning, Guangxi, 530200, China;
3. School of Basic Medical Science, Guangxi Medical University, Nanning, Guangxi, 530021, China
第五代移动通信(5G)延续了传统移动通信系统稳定、高速、可靠的特点,使得具有高计算性能智能终端设备数量和数据流量呈爆炸式增长,这给传统的能量受限的无线通信网络带来了新的挑战[1]。在增强移动宽带、超高可靠与低时延通信、海量物联网通信三大主要场景下,5G的关键性能要求也相应提高,如在频谱效率(Spectral Efficiency,SE)方面将较传统无线网络提升4-15倍,而对能量效率的需求也将提升百倍以上,以实现真正意义上的绿色通信。
能量收集技术是从周围环境中提取和收集能量,用于能量存储或用作设备后续运行的驱动力。电磁波本身就是一种能量载体,通信设备发出的射频(Radio Frequency,RF)信号既是信息的载体也是能量的载体,可实现能量和信息的同步传输。因此,以RF信号为能量收集对象的相关研究受到了业界的广泛关注。在能量收集无线网络中,可大致分为基于发射端的无线供能通信网络(Wireless Powered Communication Networks,WPCN)和基于接收端的无线携能通信(Simultaneous Wireless Information and Power Transfer,SWIPT)[2]。
目前,基于无线能量传输(Wireless Power Transmission,WPT)的能量收集技术已经成为受能量限制的无线通信网络的关键候选技术[3-6]。而备受工业界青睐的一种无线能量收集方法是在传统蜂窝网络中部署一种低成本、不需要回程链路的设备,即能量信标(Power Beacons,PB),该设备在无线网络中只提供专用的能量传输[7]。例如,Wang等[8]在大规模传感器网络中提出了一种自适应定向波束无线能量传输方案,并基于波束功率强度和传感器数量之间权衡的考虑提出3种无线能量传输方案。Liu等[9]研究大规模认知蜂窝网络中的安全D2D(Device-to-Device)通信问题,提出3种无线能量传输方案,从配备了多天线的PB中获取能量,然后使用宏基站(Base Station,BS)的频谱与相应的接收机进行安全通信。Guo等[10]通过随机几何工具分析了基于SWIPT的PB辅助的自组网络(Ad Hoc Network)的中断概率。然而,上述工作均是基于传统低于6 GHz频段(Sub-6GHz)部分频谱的研究,没有进一步考虑频谱效率的要求。
毫米波(mmWave)段高频具有频谱资源丰富且干净、可实现高速率传输、少有干扰源等优点,采用高频mmWave进行短距离通信可以获得大量频谱资源,显著提高5G移动网络系统吞吐量和频谱效率。目前,采用mmWave进行WPT和无线信息传输(Wireless Information Transmission,WIT)的研究已取得一定进展,如Zhai等[11]考虑5G频率下的SWIPT网络设计和优化,设计了一个融合5G低频(Low Frequency,LF)和高频(High Frequency,HF)信道的双频SWIPT网络;Khan等[12]和Wang等[13]分别对Sub-6GHz和mmWave两个频段的WPT和WIT进行性能比较,结果表明mmWave在能量收集和网络吞吐量方面比Sub-6GHz具有更好的效果。但是mmWave具有高路径损耗和对障碍物敏感的缺点,并不适合远距离传播。为了克服mmWave的高路径损耗,一些研究采用多天线技术来增加天线增益。例如,Liu等[14]和Barati等[15]提出了基于定向波束成形技术的mmWave定向传输机制。Liu等[16]在对mmWave波束训练的基础上提出了穷举搜索和分层搜索的波束对准方法来实现定向传输。Liu等[17]构建了一个典型的高低频混合组网的mmWave小型蜂窝小区,提出了2种经典的波束对准方法,给出了2个为该场景设计的波束对准方案。Psomas等[18]研究了无线能量传输与mmWave通信在无线传感器网络中的技术结合,提出了4个不同复杂度的位置感知扇区选择方案。这些研究表明,虽然采用定向波束成形技术进行mmWave传输可以提高频谱效率,但是却没有考虑多天线所带来的能源消耗问题。
除了从技术改进方面入手外,研究者还将mmWave技术应用于短距离D2D通信场景之中,在提高频谱效率的同时能降低系统能耗。Giatsoglou等[19]利用mmWave的方向性来增加D2D链路之间的频谱资源复用,减轻D2D通信在Sub-6GHz频段上共信道干扰。Niu等[20]利用定向波束成形技术实现mmWave的高速回程,通过并发传输调度和功率控制将能耗最小化。Niu等[21]研究了在mmWave小单元中实现D2D通信的节能多播调度问题,提出了一种高效节能的组播调度方案,通过调整链路的传输功率来降低能耗并确保吞吐量。另外,一些学者将mmWave应用于PB辅助的无线蜂窝网络之中。Khan等[22]研究了PB和能量收集器组成的大规模网络中WPT问题。Zhou等[23]提出了一种PB辅助mmWave的无线Ad-hoc网络。Kuang等[24]通过联合优化频谱资源块分配、能量收集时隙以及发射功率,解决基于能量收集的异构网络中D2D通信的平均能量效率问题。Lee等[25]提出了一种基于深度学习的资源管理方法,使D2D接收机可采用功率分流的工作方式实现SWIPT。在以上的研究中,每个发射机从所有的PB中收集能量,然后利用所收集到的能量将信息发送给所需的接收机,并采用随机几何工具分析系统中断概率,但未考虑系统能耗的问题。
综上所述,在移动通信中采用PB和mmWave技术进行无线能量与信息传输比传统BS服务的蜂窝网络具有更大的优势,但至今没有一个适应于5G实际发展需求的边缘网络结构模型以及同时权衡频谱效率和能耗管理的策略方案。为此,本研究基于5G无线网络,以提高频谱效率和减小能耗为目标,重点考虑在5G高低频混合组网的蜂窝网络边缘侧的一个小单元场景内(如高速热点网络、车联网或小蜂窝)的通信问题,构建一个适应5G发展的新型网络结构,并提出使该系统正常运行的最低功耗方案,实现在满足频谱效率和能量覆盖率条件下最小化系统能耗,确保整个小单元能够维持正常边缘移动通信。
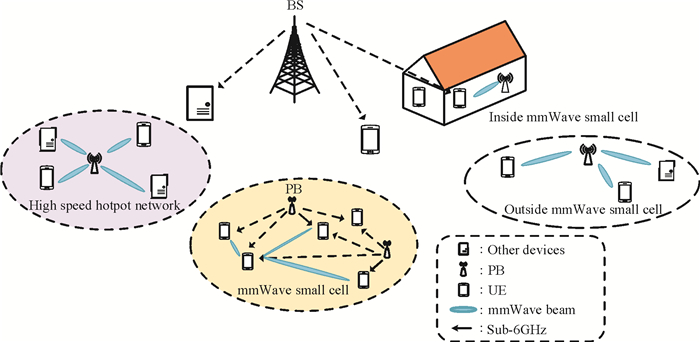
1 系统模型 1.1 网络模型构建本研究考虑如图 1所示的5G高低频混合组网的蜂窝小区。在BS覆盖的范围之内,有多个适合采用mmWave技术传输的mmWave小单元(small cell),例如需要大量数据流量的室内或室外小蜂窝、需要提供高速接入和回程服务的高速热点网络以及支持新兴自动驾驶的车联网等。其中BS工作在Sub-6GHz频谱范围,为其他的mmWave小单元提供额外的信号服务。由于采用mmWave通信,mmWave小单元与宏小区工作在不同的频带之上,故可以避免宏小区和mmWave小单元之间的干扰。此外,由于mmWave具有定向传输、较高的路径损耗、对阻塞敏感等特点,因此mmWave小单元之间的干扰几乎可以忽略不计。
|
| 图 1 5G高低频混合组网的蜂窝小区 Fig. 1 5G high-low frequency hybrid networking cellular cell |
Huang等[26]的研究表明,在宏基站中断的情况下,在蜂窝网络中部署PB,并由PB为蜂窝用户提供上行传输能量是可行的。为此,本研究考虑在5G场景下,高低频混合组网的蜂窝网络边缘侧的一个小单元内(例如高速热点网络、车联网或小蜂窝),该小单元内不包含宏基站(即不考虑从宏基站收集能量及与宏基站发生数据传输),只包含若干PB和随机独立分布的能量受限型用户设备(User Equipment Devices,UE),分别用集合Φp和Φu表示。由于不含宏基站,在模型中,PB工作在Sub-6GHz频段并周期性地为小单元内的所有UE供能,以确保整个小单元能正常运行,而信息的传输与交换则通过mmWave只发生在UE之间。值得注意的是,本研究假设从室内到室外的损耗很高,所有的PB和UE都可以看作是户外设备。
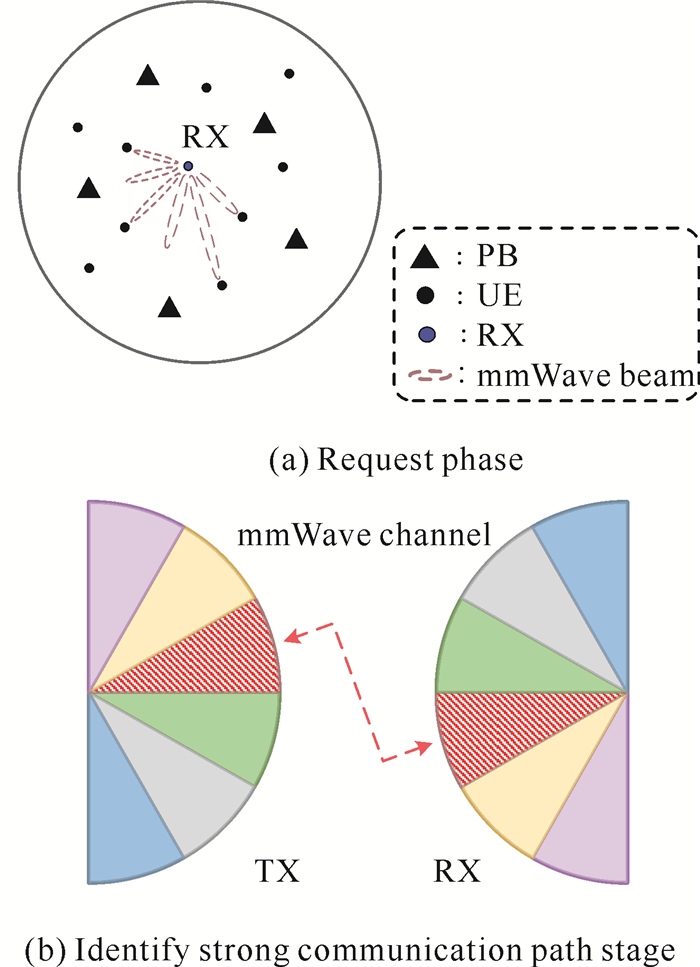
1.2 协作配对策略为了更好地描述UE之间的无线能量与信息传输,将UE分为发射机(Transmitters,TX)和接收机(Receivers,RX),并提出一个新型的UE之间协作配对策略,称为“Build to Order(BTO)”,即“需求-选择-建链”模式的新型配对策略(图 2)。
|
| 图 2 UE协作配对协议 Fig. 2 Protocol of UE cooperative pairing |
在目的接收机请求阶段[图 2(a)],RX通过向小单元内其他UE发送请求信号;收到请求信号的UE搜索自身信息,若其自身存在RX所需的信息内容则被标记为备选源发射机。在选择最佳源发射机阶段,带有所需信息内容的备选源发射机均采用mmWave波束向RX发送信号。由于mmWave信道具有稀疏性的特点,因此在该选择阶段采用定向波束成形技术识别强通信路径[图 2(b)],选择满足传播性能最佳的信道,以进行最佳源发射机与目的接收机的配对。在确定最佳源发射机之后,UE之间就完成配对(即确定TX到RX的具体链路)。此时,TX向RX发送mmWave信号,由于该mmWave波束既是信息的载体也是能量的载体,RX通过SWIPT技术将TX发送的波束用于能量收集和信息解码。
1.3 能量收集模型假设每个PB可以访问专用电源(如:接入电网),并以恒定功率Pp全向地发射RF信号并为小单元内的UE提供能量。一旦UE的能量收集电路被激活,在任意位置的UE所能收集到的能量假定是线性正比于接收总功率和能量转化效率η(0 < η < 1),则假设在位置u处的UE从PB处所能收集到的能量可以表示为
| $ P_u=\eta P_p\left\|h_{(p, u)}\right\|{ }^2 L\left(r_{(p, u)}\right), $ | (1) |
其中,h(p, u)为PB与UE之间的小尺度信道衰落效应,是服从零均值、单位方差的复高斯分布。假设本研究中所有信道为准静态衰落,即每个传输块的信道系数为常数,不同传输块之间独立变化。L(r(p, u))=r(p, u)-α为路径损耗,依赖于PB与UE之间的欧几里得距离r(p, u);α为路径损耗因子,2≤α≤4。
1.4 mmWave信道模型在TX-RX链路阶段,采用mmWave进行能量与信息的联合传输,采用Di Renzo等[27]提出的三态阻塞模型,即:①如果不存在阻塞,则链路状态为视距状态(LOS);②若存在阻塞,则链路状态为非视距状态(NLOS);③若链路太弱,则称为中断状态(OUT)。
在上述3种链路状态下,mmWave信道经历不同的信道条件,对其信道衰落h(T, R),当链路处于LOS状态时,采用Nakagami-m衰落,服从伽马分布;当链路处于NLOS状态时,服从瑞利衰落分布。相应地,对于路径损耗L(r(T, R)),可以用以下分段函数表示:
| $ L\left(r_{(T, R)}\right)=\left\{\begin{array}{cc} r_{(T, R)}{ }^{-\alpha_\text{L}}, & \text { LOS } \\ r_{(T, R)}{ }^{-\alpha_\text{N}}, & \text { NLOS }, \\ \infty, & \text { OUT } \end{array}\right. $ | (2) |
其中,r(T, R)是TX到RX的欧几里得距离,αL表示链路在LOS状态下的路径损耗,αN表示链路在NLOS状态下的路径损耗(2≤αL≤αN),并假设当链路处于OUT状态时路径损耗为无穷大。
1.5 能量与信息联合传输在PB为UE供能阶段,当UE所能收集到的能量大于激活阈值γPT时,称为激活的UE,所有满足能量收集阈值的UE用集合Фactive表示(Фactive
| $ \begin{array}{l} \;\;\;\;SINR_y= \\ \frac{P_{X_0}\left|h_{(0, y)}\right|{ }^2 L\left(r_{(0, y)}\right)}{\sum\nolimits_{X_i \in \varPhi_{\text {active }}, i \neq 0} P_{X_i}\left|h_{(i, y)}\right|^2 L\left(r_{(i, y)}\right)+\sigma^2}, \\ \end{array} $ | (3) |
式中,
根据香农定理,采用mmWave进行通信的位于y处UE的吞吐量Ry为
| $ R_y=W \log _2\left(1+S I N R_y\right) 。$ | (4) |
其中,W是mmWave带宽。
1.6 性能指标在传统移动通信系统中,频谱效率是一个衡量系统性能的关键指标。但传统的频谱效率指标只是一个流量负荷度量,不是吞吐量密度。如前所述,5G在频谱效率方面要求将提高4-15倍,并且随着超密集小区、大规模多输入多输出等新技术的采用及部署,传统的频谱效率表征系统已经不够全面。因此,在考虑蜂窝网络空间特性的基础上,本研究提出使用区域频谱效率(Area Spectrum Efficiency,ASE)来表示区域内所有用户的平均频谱效率,该指标衡量了整个系统的网络行为。在给定区域A内的ASE[用S(A, R)表示]定义为
| $ S(A, R)=\frac{\sum\nolimits_{y \in \varPhi_u} R_y}{W|A|}, $ | (5) |
即单位带宽单位面积内的吞吐量之和,式中
本研究的目标是在满足区域频谱效率约束下,最小化固定充电的PB数量Np,并规划每个PB的最佳部署方案,从而保证系统能够正常运行。因此,上述优化问题Ρ的数学模型描述如下:
| $ \begin{array}{l} \;\;\;\min\limits _{N_p}\left|N_p\right| \\ \text{s. t.} S(A, R) \geqslant S_{t h}^* \\ N_p \subseteq \varPhi_p \\ P_{u \in \varPhi_u} \geqslant \gamma_{P T}, \end{array} $ | (6) |
其中,Sth*为该区域内的目标ASE;Φp是预置的PB集合,显然所要求解的最少PB个数|Np|是Φp的子集;γPT为激活阈值。另外,需要保证区域内所有的UE都能通过收集PB发射的能量而进行下一步的信息传输,即覆盖率达到100%。问题(6)是一个混合整数规划问题,具有多项式复杂程度的非确定性(Non-deterministic Polynomial Hard,NP-难)性质,直接求其最优解是困难的。为此,本研究考虑用一个近似算法来求解,在降低复杂度的同时获得良好的性能。
为设计一个有效的算法来求解该最优化问题,对集合Bn、Bp,构造一个ASE增量函数F,若在Bn基础上加入Bp, 所能获得的ASE增量可以表示为
| $ F\left(B_p\right)=S\left(B_n \cup B_p\right)-S\left(B_n\right) 。$ | (7) |
定理1:ASE的增量函数F满足子模性。
证明:首先,对于
| $ \begin{array}{l} \;\;\;\;\quad\left|C_k\left(N_p \cup\{k\}\right)\right| \geqslant\left|C_k{ }^{\prime}\left(N_p^{\prime} \cup\left\{k^{\prime}\right\}\right)\right| \Rightarrow \\ S\left(N_p \cup\{k\}\right)-S\left(N_p\right) \geqslant S\left(N_p^{\prime} \cup\left\{k^{\prime}\right\}\right)- \\ S\left(N_p^{\prime}\right), \end{array} $ | (8) |
即:假设第k个PB的部署比第k′个PB的部署所能激活的UE更多,称PBk比PBk′有更大的能量收集覆盖率;又以等功率Pp发送能量信号的PB若在其覆盖区域内能使更多的UE被激活,则其覆盖区域内所能获得的信息量更大。根据式(5),显然部署第k个PB比部署第k′个PB能获得更高的ASE增益。
为证明ASE的增量函数F的子模性,需要证明:
| $ \begin{array}{l} \;\;\;\;\;\;\;F\left(N_p \cup\{k\}\right)-F\left(N_p\right) \geqslant F\left(N_p{ }^{\prime} \cup\{k\}\right)- \\ F\left(N_p^{\prime}\right) 。\end{array} $ | (9) |
通过上述假设,能量收集覆盖率函数满足:
| $ \left|C_k\left(N_p \cup\{k\}\right)\right| \geqslant\left|C_k\left(N_p^{\prime} \cup\{k\}\right)\right|, $ | (10) |
可得:
| $ \begin{array}{l} \;\;\;\;\;\;\;S\left(N_p \cup\{k\}\right)-S\left(N_p\right)=F\left(N_p \cup\{k\}\right) \geqslant \\ S\left(N_p^{\prime} \cup\{k\}\right)-S\left(N_p^{\prime}\right)=F\left(N_p^{\prime} \cup\{k\}\right) 。\end{array} $ | (11) |
又ASE的增量函数F是单调增函数,则对Np
| $ F\left(N_p\right) \leqslant F\left(N_p^{\prime}\right) 。$ | (12) |
联合式(11)与式(12)可得式(9),由此证明了ASE的增量函数F具有子模性。
由于ASE的增量函数F满足子模性,因此为求问题P的最优解可以采用一个常数趋近因子的贪心算法进行求解。算法描述如下:
输入:PB发射功率Pp,能量转化效率η,路径损耗因子α、αL和αN,高斯白噪声功率σ2。
输出:满足约束条件的最少PB数量Np*的集合。
① 初始化Np*=
② while S(A, Np*) < Sth do
③ for each node k∈Φp
④ 计算备选节点的能量收集覆盖率并排序;
⑤ end for
⑥
⑦
⑧ end while
⑨ return Np*
为了分析评估上述贪心算法的性能,给出以下定理。
定理2:通过贪心算法可获得(
证明:根据子模性最大问题(SMP)的证明,Nemhauser等[28]研究了一个非减子模函数的最大化问题,得出以下结论:
当G(
| $ \max\limits_Z G(Z) \text { s. t. }|Z| \leqslant K \text {, } $ | (13) |
其中, G表示目标问题,Z是找到这个目标问题的最优解的值,K是一个有限集。
可得:
| $ \frac{G(\text { greedy })}{G(\text { optimal })} \geqslant 1-\left(\frac{K-1}{K}\right)^K, $ | (14) |
其中,G(greedy)表示通过贪心算法得到的解,G(optimal)表示问题的最优解。
而对于本研究中的ASE增量函数F,前面已经证明F(
| $ \begin{array}{l} \;\;\;\;\;\;\frac{F\left(N_p^{\text {greedy }}\right)}{\max\limits_{\left|N_p\right|=\left|N_p^{\text {greedy }}\right|} F\left(N_p\right)} \geqslant \\ 1-\left(\frac{\left|N_p^{\text {greedy }}\right|-1}{\left|N_p^{\text {greedy }}\right|}\right)^{\left|N_p^{\text {greedy }}\right|} \geqslant 1-\frac{1}{e} 。\\ \end{array} $ | (15) |
因此,证明了本研究所提的贪心算法保证能找到一个常数因子近似解。
3 数值仿真与性能分析 3.1 实验环境与参数设置实验仿真出于实际情况考虑,模拟了一个1 000 m×1 000 m区域内包含200个UE的场景。由于真实场景下通常不可能临时布置PB,只能通过预置固定PB,在满足区域频谱效率约束下,利用每个预置PB的开关完成对固定充电的PB的最佳选择部署。从真实场景进行考虑使得本研究所构建的边缘小单元网络模型更适应5G实际发展的需求,同时在此类真实场景的网络模型基础上讨论其频谱效率和能耗管理的权衡策略方案更为妥当。因此,本研究考虑将边缘小单元网络网格化,预置固定充电的PB,并采用均匀分布,同时PB上配备开关,其中每两个候选PB之间间隔100 m,当满足条件时则选取相应的PB作为部署。
前期已有学者通过研究论证采用PB为蜂窝用户提供上行传输能量及利用mmWave进行UE间信息交换的可行性[9, 23, 26]。本研究在此基础上考虑小单元内的UE通过WPT从PB收集能量,以便UE间可以采用mmWave进行信息传输的场景,从而实现在确保整个小单元能够维持正常边缘移动通信的前提下最小化系统能耗。因而,如无特殊说明,采用Liu等[9]和Zhou等[23]研究的mmWave信道和WPT参数作为本研究的仿真实验参数(表 1)。每个仿真实验值均为执行算法100次后生成的100个随机拓扑的平均值。
| 参数 Parameter |
参数值 Parameter value |
| PBs transmit power | 40 dBm |
| Energy conversion efficiency | 0.8 |
| Path-loss exponent of PB-UE link | 3 |
| Path-loss exponent of mmWave LOS | 2 |
| Path-loss exponent of mmWave NLOS | 4 |
| Energy harvesting threshold | -20 dBm |
| Additive White Gaussian Noise (AWGN) | -30 dBm |
| MmWave bandwidth | 28 GHz |
3.2 算法的有效性
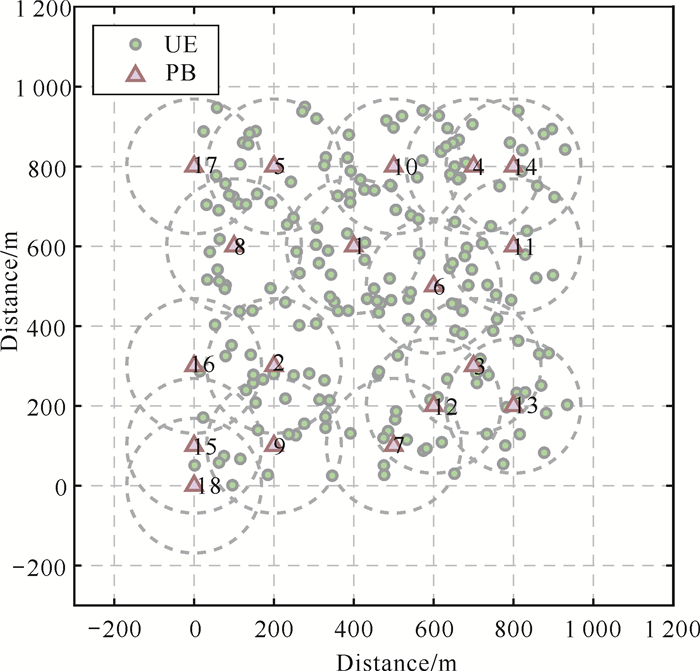
本小节对算法的有效性进行验证。图 3给出了采用本研究所提的贪心算法所获得的最少PB的图例。为了更好地显示PB的覆盖范围,用虚线圆圈表示每个PB所能覆盖的范围,圈内的点即为该PB所能服务的UE,并将边界扩到1 500 m×1 500 m。采用本研究算法,每次选择出最佳PB,控制区域内预置的PB开关,直到此区域内所有用户都能进行通信。结果显示,每次都是从覆盖UE最多、能带来当前最大ASE增量的PB开始选择。从图 3可以看到,对于200个UE,选出18个PB就可以达到目标要求。
|
| 图 3 采用算法部署PB的实例 Fig. 3 Instance of PB deployment |
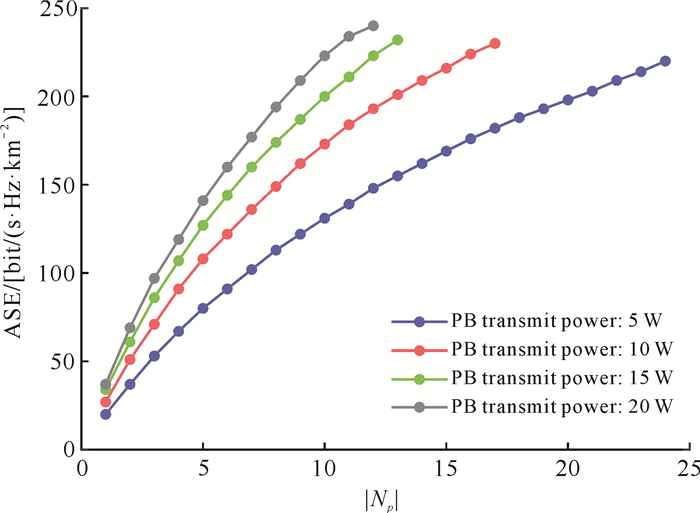
为了评估算法的有效性,图 4给出了在实验区域内随机分布200个UE的情况下,采用本研究的贪心算法部署不同发射功率的PB对系统ASE增量的影响。将Pp分别设置为5、10、15、20 W,其原因如下:首先,此发射功率对于人体来说是安全的[29];然后,当Pp很小时,则根据公式(1)在UE所能收集到的能量Pu小于激活阈值γPT,不足以被激活进而参与后续的信息交换阶段;最后,本研究的目标是在满足区域频谱效率和能量覆盖率条件下最小化系统能耗,实现绿色通信,因此出于能耗管理策略方案的考虑,当发射功率超过20 W时,能耗会大大增加。从图 4可以看出,随着|Np|的增大,ASE增加的速率逐渐减小,这很好地验证了定理1的正确性。另外,为了达到200 bit/(s·Hz·km2)的ASE,需要5-20 W的PB大致分别为20、13、10、8个。然而从能耗方面考虑,虽然布置5 W情况下所需PB的数量是4种情况下最多的,甚至是布置20 W情况下所需PB的2.5倍,但却节约了近40%的能耗。
|
| 图 4 PB发射功率对ASE增量影响 Fig. 4 Effect of different types of PB on ASE gains |
3.3 算法性能分析与对比
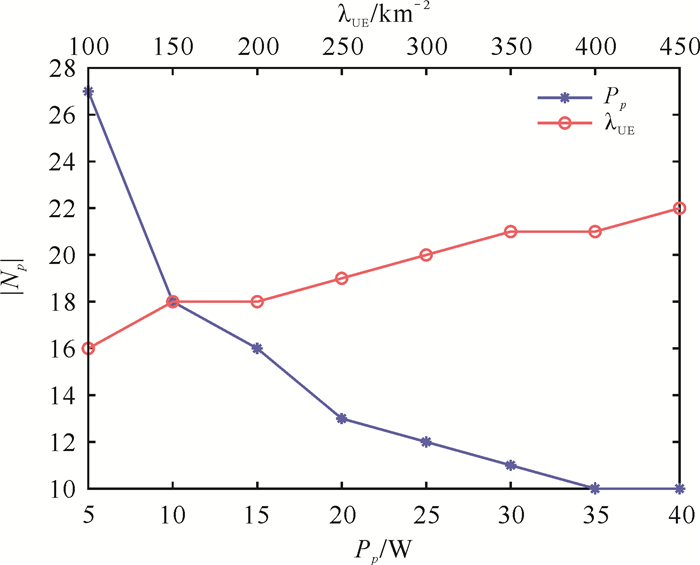
为了探讨各种参数对最小化工作PB数量的影响,实验模拟了在不同Pp和不同UE密度λUE(每平方千米内UE的数量)下,所要求最小工作的PB的数量|Np|,实验结果如图 5所示。对于200个UE,实验的Pp为5-40 W,因为根据电气与电子工程师协会(Institute of Electrical and Electronics Engineers,IEEE)标准,人体暴露于该范围内的功率下是安全的[29]。从图 5可看出,在安全发射功率范围内,工作PB的|Np|一开始随着Pp的增大而急剧减小;随后当发射功率Pp>20 W且区域内UE相对分散时,为达到100%能量覆盖率的约束条件,|Np|受Pp的影响逐渐减小。而对固定Pp =40 dBW(10 W)情况下,|Np|虽然随λUE的增大而增大,但增幅相对平稳。这是因为当区域内UE越密集时,用尽可能少的PB就能完成区域内所有用户的能量覆盖。
|
| 图 5 Pp和λUE对部署PB的影响 Fig. 5 Effect of Pp and λUE on the deployment of PB |
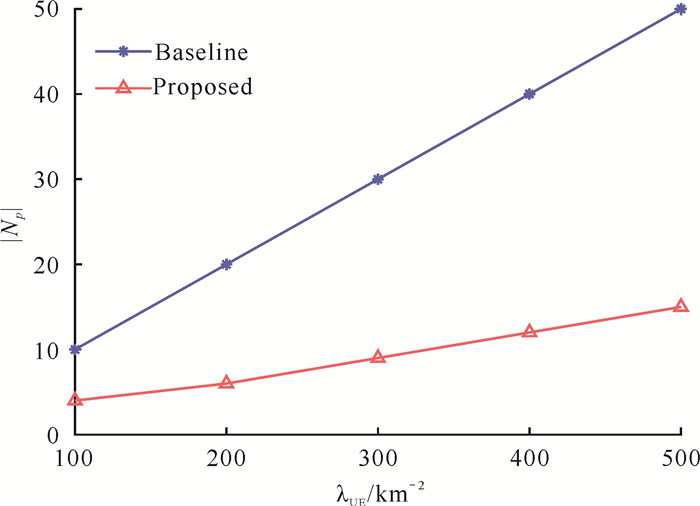
为了比较分析本研究所提出方案的性能,采用Zhou等[23]提出的部署方案作为对比。但是,Zhou等[23]提出的方案与本研究工作有所不同,该研究主要关注不同PB密度λPB、Pp、γPT对网络的能量覆盖率的影响,没有考虑系统能耗问题,故直接进行比较不合适。为此,本研究借鉴Zhou等[23]的设计思想,设置了基准参考线,其中每个点表示在该文献中的参考λUE和能量覆盖率下,需要部署的PB数量。实验模拟是在相等λUE和能量覆盖率下,采用本研究算法所需的最小|Np|。对比结果如图 6所示,可知为了达到与Zhou等[23]相同的覆盖率,采用本研究方案可减少部署30%以上的PB,从而大大减少系统能耗。
|
| 图 6 不同覆盖率和λUE下部署PB个数对比 Fig. 6 Comparison of the number of deployed PB under different coverage and λUE |
4 结论
本研究将能量收集技术应用于5G高低频混合组网蜂窝网络的边缘侧,构建一个不含传统宏基站(BS)、只包含若干随机分布的UE和PB的蜂窝小单元新型网络模型, 在该小单元中采用PB代替BS,周期性地为小单元内的所有UE提供能量补给;提出了一个新型的UE之间协作配对策略,设计一个BTO模式的新型建链协议,将mmWave定向传输技术应用于该建链过程之中。基于所提模型和协议,在ASE和能量覆盖率联合约束下,提出最小化固定充电的PB数量的部署方案,从而在减少能耗的基础上保证该系统能够正常运行。针对该最优化问题是一个混合整数规划问题,被证明为NP-难问题,提出一个常数因子的近似求解算法求解该最优化问题,并给出理论证明。仿真实验结果表明,本研究提出的算法在相同能量覆盖率情况下,可以减少部署30%的PB,从而实现降低系统能耗的目的。
| [1] |
李陶深, 朱晴, 王哲, 等. 基于5G的无线携能通信技术研究与发展[J]. 广西科学, 2021, 28(3): 229-241, 331. |
| [2] |
CLERCKX B, ZHANG R, SCHOBER R, et al. Guest editorial wireless transmission of information and power: part Ⅱ[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(2): 249-252. DOI:10.1109/JSAC.2018.2872384 |
| [3] |
HUANG Y W, LIU Y, LI G Y. Energy efficiency of distributed antenna systems with wireless power transfer[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(1): 89-99. DOI:10.1109/JSAC.2018.2872362 |
| [4] |
CHANG Z, WANG Z, GUO X, et al. Distributed resource allocation for energy efficiency in OFDMA multicell networks with wireless power transfer[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(2): 345-356. DOI:10.1109/JSAC.2018.2872398 |
| [5] |
周叶宁, 李陶深, 王哲, 等. 具有SWIPT和自能量回收的非分时全双工中继系统[J]. 计算机研究与发展, 2020, 57(9): 1888-1897. |
| [6] |
李陶深, 施安妮, 王哲, 等. 基于SWIPT的吞吐量最优化NOMA全双工中继选择策略[J]. 通信学报, 2021, 42(5): 87-97. |
| [7] |
LU X, WANG P, NIYATO D, et al. Wireless networks with RF energy harvesting: a contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 757-789. |
| [8] |
WANG Z, DUAN L, ZHANG R. Adaptively directional wireless power transfer for large-scale sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(5): 1785-1800. DOI:10.1109/JSAC.2016.2551619 |
| [9] |
LIU Y, WANG L, ZAIDI S A R, et al. Secure D2D communication in large-scale cognitive cellular networks: a wireless power transfer model[J]. IEEE Transactions on Communications, 2016, 64(1): 329-342. DOI:10.1109/TCOMM.2015.2498171 |
| [10] |
GUO J, DURRANI S, ZHOU X, et al. Outage probability of ad hoc networks with wireless information and power transfer[J]. IEEE Wireless Communications Letters, 2015, 4(4): 409-412. DOI:10.1109/LWC.2015.2427163 |
| [11] |
ZHAI D, ZHANG R, DU J, et al. Simultaneous wireless information and power transfer at 5G new frequencies: channel measurement and network design[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(1): 171-186. DOI:10.1109/JSAC.2018.2872366 |
| [12] |
KHAN T A, ALKHATEEB A, HEATH R W. Millimeter wave energy harvesting[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6048-6062. DOI:10.1109/TWC.2016.2577582 |
| [13] |
WANG L, WONG K K, HEATH R W, et al. Wireless powered dense cellular networks: how many small cells do we need?[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 2010-2024. DOI:10.1109/JSAC.2017.2720858 |
| [14] |
LIU C, LI M, COLLINGS I B, et al. Design and analysis of transmit beamforming for millimeter wave base station discovery[J]. IEEE Transactions on Wireless Communications, 2017, 16(2): 797-811. DOI:10.1109/TWC.2016.2630681 |
| [15] |
BARATI C N, HOSSEINI S A, MEZZAVILLA M, et al. Initial access in millimeter wave cellular systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(12): 7926-7940. DOI:10.1109/TWC.2016.2609384 |
| [16] |
LIU C, LI M, HANLY S V, et al. Millimeter wave beam alignment: large deviations analysis and design insights[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(7): 1619-1631. |
| [17] |
LIU C, LI M, HANLY S V, et al. Millimeter-wave small cells: base station discovery, beam alignment, and system design challenges[J]. IEEE Wireless Communications, 2018, 25(4): 40-46. DOI:10.1109/MWC.2018.1700392 |
| [18] |
PSOMAS C, KRIKIDIS I. Energy beamforming in wireless powered mmWave sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(2): 424-438. DOI:10.1109/JSAC.2018.2872381 |
| [19] |
GIATSOGLOU N, NTONTIN K, KARTSAKLI E, et al. D2D-aware device caching in mmWave-cellular networks[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 2025-2037. DOI:10.1109/JSAC.2017.2720818 |
| [20] |
NIU Y, GAO C, LI Y, et al. Energy-efficient scheduling for mmWave backhauling of small cells in heterogeneous cellular networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2674-2687. DOI:10.1109/TVT.2016.2582785 |
| [21] |
NIU Y, LIU Y, LI Y, et al. Device-to-device communications enabled energy efficient multicast scheduling in mmWave small cells[J]. IEEE Transactions on Communications, 2018, 66(3): 1093-1109. DOI:10.1109/TCOMM.2017.2773529 |
| [22] |
KHAN T A, HEATH R W. Wireless power transfer in millimeter wave tactical networks[J]. IEEE Signal Processing Letters, 2017, 24(9): 1284-1287. DOI:10.1109/LSP.2017.2715324 |
| [23] |
ZHOU X, GUO J, DURRANI S, et al. Power beacon-assisted millimeter wave ad hoc networks[J]. IEEE Transactions on Communications, 2018, 66(2): 830-844. DOI:10.1109/TCOMM.2017.2766152 |
| [24] |
KUANG Z, LIU G, LI G, et al. Energy efficient resource allocation algorithm in energy harvesting-based D2D heterogeneous networks[J]. IEEE Internet of Things Journal, 2019, 6(1): 557-567. DOI:10.1109/JIOT.2018.2842738 |
| [25] |
LEE K, HONG J P, SEO H, et al. Learning-based resource management in device-to-device communications with energy harvesting requirements[J]. IEEE Transactions on Communications, 2020, 68(1): 402-413. DOI:10.1109/TCOMM.2019.2947514 |
| [26] |
HUANG K, LAU V K N. Enabling wireless power transfer in cellular networks: architecture, modeling and deployment[J]. IEEE Transactions on Wireless Communications, 2014, 13(2): 902-912. DOI:10.1109/TWC.2013.122313.130727 |
| [27] |
DI RENZO M, LU W, GUAN P. The intensity matching approach: a tractable stochastic geometry approximation to system-level analysis of cellular networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 5963-5983. DOI:10.1109/TWC.2016.2574852 |
| [28] |
NEMHAUSER G L, WOLSEY L A, FISHER M L. An analysis of approximations for maximizing submodular set functions: Ⅰ[J]. Mathematical Programming, 1978, 14(1): 265-294. DOI:10.1007/BF01588971 |
| [29] |
XIA M, AISSA S. On the efficiency of far-field wireless power transfer[J]. IEEE Transactions on Signal Processing, 2015, 63(11): 2835-2847. DOI:10.1109/TSP.2015.2417497 |



