技能优化算法(Skill Optimization Algorithm, SOA)[1]的灵感来自人们努力获取和提高技能的行为,具有寻优能力强、操作简单等特点,现已经被应用于PID (Proportional Integral Derivative)参数整定等方面[2],在众多智能优化算法中有很强的竞争力,但是SOA存在搜索能力不足、收敛速度慢等问题,其性能仍有较大的提升空间。
为了提高智能算法的性能,诸多学者提出了不同的改进策略。为解决随机初始化导致初始种群不均匀的问题,学者们提出了佳点集、混沌映射以及拉丁超立方抽样等方法来改善初始种群的分布。石建平等[3]利用佳点集方法初始化果蝇优化算法的初始种群,在一定程度上提高了果蝇优化算法的寻优精度;Wang等[4]采用tent混沌映射初始化蜻蜓优化算法初始种群,提高了算法的搜索效率;He等[5]通过拉丁超立方抽样方法初始化烟花算法,提高了初始种群的分布状况。除此之外,为了提高收敛速度、加强算法寻优能力,自适应权重被广泛运用于改进各种优化算法。郑洪清等[6]根据蝴蝶优化算法的特点,在蝴蝶优化算法自身认知部分引入非线性自适应权重,显著提高了蝴蝶优化算法的性能;Ma等[7]利用双重自适应权重改进灰狼优化算法的狩猎行为,提高了算法的收敛精度。为了改善算法局部搜寻能力不足、易陷于局部最优解的情况,各种概率分布的扰动变异被用于改进各类算法。Song等[8]通过高斯分布对个体进行变异,显著提高了哈里斯鹰优化算法的种群多样性;宁杰琼等[9]对个体进行柯西-t分布扰动,增加了花授粉算法个体跳出局部最优的概率。目前,改进SOA的相关研究较少,本研究借鉴其他算法优化的研究逻辑,采用集成优化思路对SOA算法进行改进,并在应用中验证其有效性。
因此,针对SOA的不足,结合前人改进其他算法的研究逻辑,本研究提出多策略集成的改进技能优化算法(Multi Strategy integrated Skill Optimization Algorithm, MSSOA)。针对SOA算法初始化不均匀导致搜索空间不足的问题,MSSOA采用佳点集策略对种群进行初始化,该策略能够使个体更加均匀分布于搜索空间,从而增强算法的全局搜索能力。针对传统SOA算法寻优过程单一、收敛速度慢及局部寻优能力弱的问题,MSSOA采用一种基于高斯误差和迭代次数的自适应权重,该自适应权重在迭代前期下降较慢,能够充分发挥SOA较强的全局搜索能力;在迭代后期,自适应权重快速下降,既能加速种群个体收敛,又能增强算法的局部搜寻能力。针对SOA算法后期局部搜寻能力不足的问题,MSSOA在寻优过程中采用t-分布对个体进行扰动,能够平衡全局搜索和局部搜寻的关系,有效避免陷入局部最优。
1 技能优化算法SOA是一种基于人群的优化算法,其个体成员的技能状态实际上是给定优化问题的候选解。SOA算法分为“从专家处获得技能”和“基于实践和个人努力的技能改进”两个阶段,这两个阶段相互影响,使种群不断朝着目标值进化。
1.1 初始化SOA采用随机的方式进行初始化:
| $ X_i^{\mathrm{int}}=\operatorname{rand} \times(u b-l b)+l b, i=1, 2, \cdots, N, $ | (1) |
其中,Xiint为第i个初始化个体,lb和ub为探索空间的上界和下界,N为初始种群的数量,rand为0-1的随机向量。
1.2 从专家处获取技能第一阶段(从专家处获取技能)主要进行的是全局搜索。每一个成员随机选择一个适应度优于自己的成员Ei为专家成员,在专家成员的引导下,该成员朝着较优的方向进化。本研究以最小问题为例,则从专家处获取技能的方式如式(2)所示:
| $ \begin{array}{l} \;\;\;\;\;\;\;X_i^{\mathrm{new} 1}(t): X_{i, d}^{\mathrm{new} 1}(t)=X_{i, d}(t)+r\left(E_{i, d}(t)-I \times\right. \\ \left.X_{i, d}(t)\right), \end{array} $ | (2) |
其中,Ei=Xk, F(Xk) < F(Xi), k≠i, Xinew1(t)为第一阶段成员i的新技能状态,Xi, dnew1(t)为第一阶段成员i的技能状态的第d维数值,Xi, d(t)为成员i的技能状态的第d维数值,Ei为成员i所选择的专家当前的技能状态,Ei, d(t)为专家的技能状态的第d维数值,r为区间[0, 1]的随机向量,I为从{1, 2}中随机取值的向量,t为迭代次数,Xi为成员i当前的技能状态,F(Xi)代表成员i的当前技能状态适应度值。
从专家获取技能后,对学习结果进行边界控制,数学表达式如式(3)所示:
| $ X_{i, d}^{\mathrm{new} 1}(t)=\left\{\begin{array}{l} l b_{i, d}, X_{i, d}^{\mathrm{new} 1}(t)<l b_{i, d} \\ u b_{i, d}, X_{i, d}^{\mathrm{new} 1}(t)>u b_{i, d} \end{array}, \right. $ | (3) |
其中,lbi, d和ubi, d分别为成员i的技能状态的第d维的下界和上界。
然后每个成员根据自己原有的和新的技能状态来决定是否接受此次技能的学习:
| $ \begin{aligned} X_i(t) & =\left\{\begin{array}{l} X_i^{\text {new1} }(t), \text { if } F_i^{\text {new1} }(t) \leqslant F_i(t) \\ X_i(t), \text { else } \end{array}\right. \\ F_i(t) & =\left\{\begin{array}{l} F_i^{\text {new1} }(t), \text { if } F_i^{\text {new1} }(t) \leqslant F_i(t) \\ F_i(t), \text { else } \end{array} \right. \end{aligned}, $ | (4) |
其中,Finew1(t)为第一阶段后成员i的新技能状态适应度值。
1.3 基于实践和个人努力的技能改进第二阶段(基于实践和个人努力的技能改进)主要进行局部搜寻。每个成员都试图通过个人实践和活动来提高在第一阶段中获得的技能,由于成员自身探索的盲目性和不确定性,因此该阶段有两种更新自身技能的方式,其数学表达式如式(5)所示:
| $ \begin{array}{c} X_i^{\text {new2 }}(t): X_{i, d}^{\text {new2 }}(t)= \\ \left\{\begin{array}{l} X_{i, d}(t)+\frac{1-2 r}{t}, \text { if rand } \leqslant 0.5 \\ X_{i, d}(t)+\frac{l b_{i, d}+r\left(u b_{i, d}-l b_{i, d}\right)}{t}, \text { else } \end{array}\right., \\ \end{array} $ | (5) |
其中,Xinew2(t)为第二阶段成员i的新技能状态,Xi, dnew2(t)为第二阶段成员i的新技能状态的第d维数值,t为当前的迭代次数,r为区间[0, 1]的随机向量,rand为0-1的随机值。
基于实践和个人努力的技能改进后,对学习结果进行如式(6)所示的边界控制:
| $ X_{i, d}^{\mathrm{new} 2}(t)=\left\{\begin{array}{l} l b_{i, d}, X_{i, d}^{\mathrm{new} 2}(t)<l b_{i, d} \\ u b_{i, d}, X_{i, d}^{\mathrm{new} 2}(t)>u b_{i, d} \end{array} 。\right. $ | (6) |
通过自身努力更新技能后,每个成员会选择是否保留此次状态的更新,如式(7)所示:
| $ \begin{aligned} X_i(t) & =\left\{\begin{array}{l} X_i^{\text {new} 2}(t), \text { if } F_i^{\text {new2}}(t) \leqslant F_i(t) \\ X_i(t), \text { else } \end{array}\right. \\ F_i(t) & =\left\{\begin{array}{l} F_i^{\text {new2}}(t), \text { if } F_i^{\text {new2}}(t) \leqslant F_i(t) \\ F_i(t), \text { else } \end{array} \right. \end{aligned}, $ | (7) |
其中,Finew2(t)为第二阶段后成员i的新技能状态的适应度值。
第二阶段结束后对成员再次执行与第一阶段相同的更新操作。
1.4 SOA伪代码根据上述流程描述,标准SOA伪代码如下:
输入:种群规模N、最大迭代次数Tmax和函数名称。
输出:最优技能状态Xi和最优值Fi。
① 随机初始化种群Xiint,计算种群个体的技能状态以及适应度值,并记录最优个体的技能状态和最优适应度值。
② While t < Tmax
③ For i=1:N
④ 执行式(2)的全局搜索、执行式(3)的边界控制、执行式(4)的保留策略;
⑤ 执行式(5)的局部搜寻、执行式(6)的边界控制、执行式(7)的保留策略;
⑥ 记录最优个体的技能状态以及最优值。
⑦ End for
⑧ End While
2 多策略集成的改进技能优化算法(MSSOA) 2.1 种群初始化初始解的分布会对智能优化算法的收敛速度和寻优精度产生影响,均匀、多样的种群分布有利于提高算法的寻优性能[10],标准SOA采用随机的方式产生初始种群,易造成种群分布不均匀且遍历性差。佳点集方法是一种有效的均匀选点方法[10],本研究以二维、200个个体的种群为例,分别运用佳点集生成方法[10]和随机生成方法对种群进行初始化,对比结果见图 1。相较于随机初始化,运用佳点集策略初始化能够使得种群个体分布更加均匀且遍布于整个探索区域。因此本研究采用佳点集方法来初始化SOA的种群,以提高算法在解空间上的遍历能力。
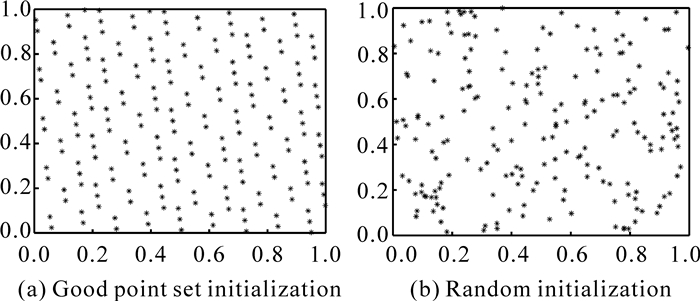
|
| 图 1 佳点集初始化和随机初始化的对比 Fig. 1 Comparison of good point set initialization and random initialization |
2.2 自适应权重
由式(2)可知,成员技能状态的更新较大程度依赖于成员现有的技能状态,若成员依靠自身现有的状态进行较大范围的搜索,虽然有利于提升算法的全局搜索能力,但是也会影响算法的寻优精度。惯性权重对成员技能状态的更新极其重要,当惯性权重较大时,算法具有较好的全局搜索能力;当惯性权重较小时,算法具有较强的局部搜寻能力,可快速搜索到最优解周围的区域,从而加快算法收敛、提高算法寻优精度。标准SOA的惯性权重恒定为“1”,不利于算法性能的进一步提升。
SOA源于人们日常生活中技能学习的过程,所以结合现实生活改进算法是较为可行的。在技能学习初期,由于对新技能的不确定和陌生,因此成员对新技能持怀疑态度,更倾向于保持原有的技能状态。随着对新技能学习的深入,成员对自身技能状态的保留随着迭代的次数增加而减少,且减少的速率逐渐加快,为了很好地刻画这一行为,本研究提出如式(8)所示的自适应权重w,并绘制w随迭代次数变化的趋势(图 2)。
| $ w=\operatorname{erf}\left(\frac{\pi}{2} \times \frac{T_{\max }-t}{t}\right), $ | (8) |
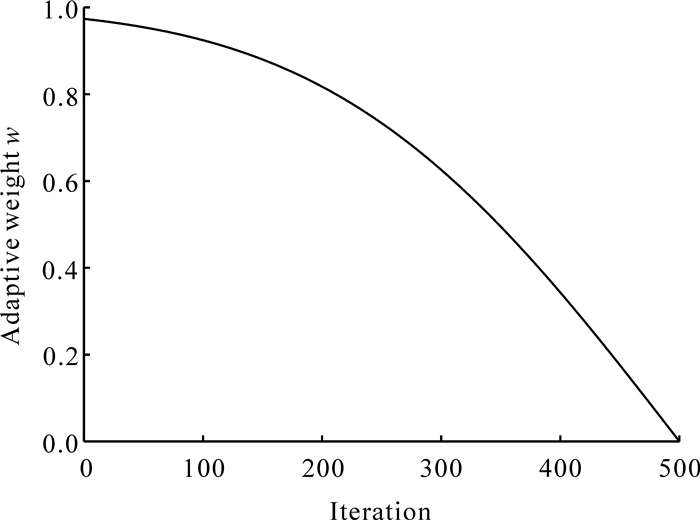
|
| 图 2 自适应权重w随迭代次数变化 Fig. 2 Variation of adaptive weight w with the number of iterations |
其中,Tmax为最大迭代次数,erf为高斯误差函数。
w在迭代初期接近于1,成员更倾向保留原有的技能状态,此时成员主要依靠自身原有的技能状态进行探索,具有较大的探索范围,能够很好地保留SOA的全局搜索能力。随着迭代的进行,w不断减小,成员快速向选择的“专家”靠近,这能够加速算法的收敛,同时也提高了算法在全局搜索过程中局部搜寻的能力,有利于提升算法的寻优精度。
通过引入自适应权重w,则第一阶段的技能状态更新表达式,由式(2)改写为式(9):
| $ \begin{array}{l} \;\;\quad X_i^{\mathrm{newl}}(t): X_i^{\mathrm{new1}}(t)=w x_{i, d}(t)+r\left(E_{i, d}(t)-I \times\right. \\ \left.x_{i, d}(t)\right), \end{array} $ |
| $ \text { 其中, } E_i=X_k, F\left(X_k\right)<F\left(X_i\right) \text {, 且 } k \neq i \text { 。} $ | (9) |
在迭代初期,由于迭代次数t较小,所以个体成员能够进行较大范围的搜索,此时算法的全局搜索能力较强,但是随着迭代次数t的增加,个体成员的搜索范围变小,这导致迭代后期算法的全局搜索能力不足,易使算法陷入局部最优。柯西变异能增强算法的全局搜索能力[11];而引入高斯变异可以保证算法收敛速度的同时提高算法跳出局部最优的能力[12]。随着自由度n的变化,t-分布能够很好地结合柯西分布与高斯分布的优点,对个体产生较大的扰动,所以本研究采用t-分布来对种群进行扰动,这不仅能保证算法的收敛速度,还能很好地平衡算法全局和局部搜寻能力,增强算法后期局部搜寻的能力。
为了充分发挥t-分布的特点,引入自然常数e的指数,让t-分布的取值随着迭代次数改变,根据SOA算法自身的特点,对不同种群成员采取不同的扰动策略。具体来说,以平均适应度为标准,对适应度较好的成员,让其自行进行t-分布扰动;对适应度较差的成员,利用“最优”个体对其进行引导扰动,公式如(10)所示:
| $ \begin{array}{l} \;\;\;\;\;\;\;X_i^{\text {new } 3}(t)= \\ \left\{\begin{array}{c} X_i(t)\left(1+t \cdot \operatorname{dis}\left(e^{t^2}\right)\right), \text { if } F_i(t) \leqslant F^{\text {mean }}(t) \\ X_i(t)+t \cdot \operatorname{dis}\left(e^{t^2}\right)\left(X_{\text {best }}(t)-X_i(t)\right), \text { else } \end{array}, \right. \end{array} $ | (10) |
其中,Xinew3(t)为t-分布扰动后成员i的新技能状态,Fmean (t)为所有成员技能状态适应度值的均值, Xbest(t)为所有成员中最优的技能状态。然后,进行如式(11)所示的边界处理,并利用式(12)所示的贪婪策略对较优个体进行保留:
| $ X_{i, d}^{\mathrm{new} 3}(t)=\left\{\begin{array}{l} l b_{i, d}, X_{i, d}^{\mathrm{new} 3}(t)<l b_{i, d} \\ u b_{i, d}, X_{i, d}^{\mathrm{new} 3}(t)>u b_{i, d} \end{array}, \right. $ | (11) |
| $ \begin{aligned} X_i(t) & =\left\{\begin{array}{l} X_i^{\mathrm{new} 3}(t), F_i^{\mathrm{new} 3}(t) \leqslant F_i(t) \\ X_i(t), \text { else } \end{array}, \right. \\ F_i(t) & =\left\{\begin{array}{l} F_i^{\mathrm{new} 3}(t), \text { if } F_i^{\mathrm{new} 3}(t) \leqslant F_i(t) \\ F_i(t), \text { else } \end{array}, \right. \end{aligned} $ | (12) |
其中,Finew3(t)为t-分布扰动后成员i的新技能状态的适应度值。
t-分布的扰动能够加强算法的探索能力,有利于提高算法的寻优精度,同时引入的“最优”个体的t-分布扰动,也能够在一定程度上加快个体向目标值靠近,加快算法的收敛速度。
2.4 MSSOA算法伪代码根据上述章节对算法的改进,MSSOA的伪代码步骤如下。
输入:种群规模N、最大迭代次数Tmax和函数名称。
输出:最优技能状态Xi和最优值Fi。
① 利用佳点集策略初始化种群Xiint,计算种群个体的技能状态以及适应度值,并记录最优个体的技能状态和最优适应度值。
② While t < Tmax
③ For i=1:N
④ 计算式(8)的惯性权重;
⑤ 执行式(9)的全局搜索、执行式(3)的边界控制、执行式(4)的保留策略;
⑥ 执行式(5)的局部搜寻、执行式(6)的边界控制、执行式(7)的保留策略;
⑦ 执行式(10)的扰动策略、执行式(11)的边界控制、执行式(12)的保留策略;
⑧ 记录最优个体的技能状态以及最优值;
⑨ End for
⑩ End While
2.5 MSSOA的时间复杂度分析在SOA中,假设种群大小为N,搜索维度为d,记SOA的初始化和计算初始种群适应度的时间复杂度分别为O(t)和O(N)、迭代过程的时间复杂度为O(Nd),因此标准的SOA的时间复杂度为
| $ O(t)+O(N)+O(N d)=O(N d) 。$ | (13) |
本研究提到的MSSOA中,在SOA的基础上初始化采用佳点集策略时间复杂度为O(Nd),更新自适应权重w的时间复杂度为O(l),执行t-分布扰动的时间复杂度为O(Nd)。因此MSSOA的时间复杂度为
| $ \begin{array}{l} \;\;\;\;\;\;O(N d)+O(N)+O(l)+O(N d)+O(N d)= \\ O(N d)。\end{array} $ | (14) |
综上所述,MSSOA与SOA的时间复杂度属于同一量级的,并没有增加。
3 实验仿真与结果分析为验证本研究所提出MSSOA的优越性能,对其进行仿真实验,主要分为2个部分:①测试函数结果对比分析,将MSSOA与多个对比算法在不同基准函数上进行优化对比,分析MSSOA的优越性;②工程应用结果对比分析,将MSSOA与多个对比算法在两个实际工程案例上进行优化对比,验证MSSOA的实际应用能力。所有实验均是在配有Intel Ⓒ Core TM i5-6300HQ CPU @ 3.2 GHz主频、4 GB运行内存和Windows 10(64位)操作系统的个人计算机上进行,并使用MATLAB 2021b编写代码。
3.1 测试函数结果对比分析 3.1.1 测试函数为了充分验证MSSOA算法性能,本研究共选取12个不同特征的测试函数进行性能测试,测试函数信息见表 1。其中:F1-F5为单峰测试函数,用于度量算法的寻优精度与收敛速度;F6-F9为多峰测试函数,F10-F12为固定维度测试函数,用于度量算法全局搜索和跳出局部最优能力。
| 函数名称 Function name |
范围 Scope |
维度 Dimension |
最优值 Optimum value |
| F1:Sphere | [-100, 100] | 30 | 0 |
| F2:Schwefel′s Problem 2.22 | [-10, 10] | 30 | 0 |
| F3:Schwefel′s Problem 1.2 | [-100, 100] | 30 | 0 |
| F4:Schwefel′s Problem 2.21 | [-100, 100] | 30 | 0 |
| F5:Quartic | [-1.28, 1.28] | 30 | 0 |
| F6:Generalized Rastrigin | [-5.12, 5.12] | 30 | 0 |
| F7:Ackley | [-32, 32] | 30 | 0 |
| F8:Levy | [-10, 10] | 30 | 0 |
| F9:Griewank | [-600, 600] | 30 | 0 |
| F10:Shekel′s Family 2 | [-10, 10] | 4 | -10.402 9 |
| F11:Shekel′s Family 3 | [-10, 10] | 4 | -10.536 4 |
| F12:Shekel′s Foxholes | [-65.536, 65.536] | 2 | 0.998 |
3.1.2 对比实验分析
利用MSSOA算法分别执行表 1所示的12个测试函数,种群大小N设置为30,固定维度测试函数按照相应维数要求设置,其余测试函数维度设置为30维,最大迭代次数Tmax设置为500次,同时为了展现MSSOA算法相较于其他算法的优越性,将其与粒子群算法(Particle Swarm Optimization, PSO)[13]、鲸鱼优化算法(Whale Optimization Algorithm, WOA)[14]和灰狼优化算法(Grey Wolf Optimizer, GWO)[15]、蜜獾优化算法(Honey Badger Algorithm, HBA)[16]和蛇优化算法(Snake Optimizer, SO)[17]等算法以及标准SOA进行对比。各算法参数设置如表 2所示。为了减少随机误差对结果的干扰,让每个算法独自运行30次,最优结果的平均值(mean)和标准差(std)分别反映算法的收敛速度和稳定性,因此通过不同算法优化各个测试函数最优结果的平均值和标准差来评判算法的性能优劣,结果见表 3。
| 算法 Algorithm |
参数 Parameters |
| SOA | / |
| HBA | C=2,β=6 |
| SO | C1=0.5,C2=0.05,C3=2 |
| PSO | W=0.75,C1,C2=2 |
| GWO | a=2-t*2/Tmax |
| WOA | a=2-t*2/Tmax |
| 函数 Function |
统计值 Statistical value |
WOA | GWO | HBA | PSO | SOA | SO | MSSOA |
| F1 | mean | 4.17E-74 | 1.66E-27 | 1.41E-135 | 1.17E+00 | 3.29E-218 | 3.48E-94 | 0.00E+00 |
| std | 1.59E-73 | 3.32E-27 | 3.49E-135 | 5.09E-01 | 0.00E+00 | 1.35E-93 | 0.00E+00 | |
| F2 | mean | 4.03E-51 | 7.25E-17 | 4.12E-72 | 9.73E+00 | 6.08E-114 | 6.63E-43 | 0.00E+00 |
| std | 1.03E-50 | 4.78E-17 | 1.62E-71 | 4.11E+00 | 2.77E-113 | 2.31E-42 | 0.00E+00 | |
| F3 | mean | 4.50E+04 | 7.77E-06 | 2.21E-96 | 7.94E+01 | 2.06E-183 | 6.34E-56 | 0.00E+00 |
| std | 1.33E+04 | 1.59E-05 | 1.19E-95 | 3.14E+01 | 0.00E+00 | 2.58E-55 | 0.00E+00 | |
| F4 | mean | 5.09E+01 | 6.88E-07 | 3.30E-56 | 5.91E+00 | 1.55E-106 | 1.21E-40 | 0.00E+00 |
| std | 2.71E+01 | 6.07E-07 | 1.37E-55 | 2.19E+00 | 4.41E-106 | 2.47E-40 | 0.00E+00 | |
| F5 | mean | 4.48E-03 | 1.63E-03 | 3.25E-04 | 8.93E-02 | 7.69E-05 | 2.10E-04 | 4.05E-05 |
| std | 5.20E-03 | 9.81E-04 | 2.56E-04 | 7.96E-02 | 5.42E-05 | 2.04E-04 | 6.99E-05 | |
| F6 | mean | 3.79E-15 | 3.23E+00 | 0.00E+00 | 8.45E+01 | 0.00E+00 | 5.61E+00 | 0.00E+00 |
| std | 1.44E-14 | 3.30E+00 | 0.00E+00 | 1.74E+01 | 0.00E+00 | 1.17E+01 | 0.00E+00 | |
| F7 | mean | 4.20E-15 | 1.09E-13 | 1.99E+00 | 5.46E+00 | 8.88E-16 | 2.42E+00 | 8.88E-16 |
| std | 2.46E-15 | 2.21E-14 | 6.08E+00 | 1.15E+00 | 0.00E+00 | 7.21E-01 | 0.00E+00 | |
| F8 | mean | 5.21E-01 | 1.16E+00 | 6.52E-01 | 9.67E+00 | 1.91E-06 | 1.02E-01 | 1.50E-32 |
| std | 2.69E-01 | 2.19E-01 | 2.06E-01 | 3.02E+00 | 5.95E-06 | 3.38E-01 | 1.11E-47 | |
| F9 | mean | 8.08E-03 | 4.01E-03 | 0.00E+00 | 3.71E-01 | 0.00E+00 | 3.75E-02 | 0.00E+00 |
| std | 3.62E-02 | 1.02E-02 | 0.00E+00 | 1.24E-01 | 0.00E+00 | 9.84E-02 | 0.00E+00 | |
| F10 | mean | -7.57E+00 | -1.04E+01 | -1.00E+01 | -8.35E+00 | -9.87E+00 | -1.03E+01 | -1.04E+01 |
| std | 3.26E+00 | 9.72E-04 | 1.71E+00 | 3.28E+00 | 1.64E+00 | 1.39E-01 | 3.85E-05 | |
| F11 | mean | -6.92E+00 | -9.72E+00 | -7.59E+00 | -8.78E+00 | -1.00E+01 | -1.05E+01 | -1.05E+01 |
| std | 3.45E+00 | 2.50E+00 | 3.72E+00 | 3.16E+00 | 1.66E+00 | 1.95E-02 | 3.12E-05 | |
| F12 | mean | 3.45E+00 | 5.01E+00 | 1.42E+00 | 2.25E+00 | 2.25E+00 | 1.30E+00 | 9.98E-01 |
| std | 3.51E+00 | 4.66E+00 | 1.81E+00 | 1.73E+00 | 1.95E+00 | 5.92E-01 | 2.14E-16 | |
| Note: bold fonts represent the best results in the experiment. | ||||||||
由表 3可知,从30次最优结果的平均值来看,对于测试函数F1-F4、F6、F9-F12,MSSOA均达到了理论最优,对于测试函数F5、F7、F8,MSSOA虽然没达到理论最优,但是其寻优精度大于等于其他6种算法,尤其是测试函数F8,MSSOA所得的优化结果远优于其他算法,从整体上看,MSSOA相较于其他6种算法有更高的寻优精度,使得种群个体能够搜索到更多局部最优解,惯性权重策略以及t-分布扰动策略提高了MSSOA的全局搜索和局部搜寻能力。从30次最优结果的标准差可以看出,除了测试函数F5之外,MSSOA的标准差是7种算法中最小的,对于测试函数F5来说,虽然MSSOA的标准差比SOA大,但二者差距很小,因此从整体上来看MSSOA仍具有优于其他6种算法的优化稳定性和鲁棒性。MSSOA的寻优精度和稳定性优于对比算法,主要是因为佳点集初始化种群提高了初始种群的质量,为算法整体性能的提高奠定了基础;自适应权重策略和t-分布扰动策略的加入,进一步提高了算法的全局搜索和局部搜寻能力,进而提高了算法寻优精度,因此MSSOA有较为理想的寻优精度。3种策略的集成使得MSSOA在每个测试函数的寻优均表现优异,所以MSSOA的寻优稳定性也得到了有效提高。综上所述,MSSOA相较于其他6种算法有更高的寻优精度以及更好的稳定性和鲁棒性。
为了更加直观反映MSSOA的整体性能,本研究给出各算法在30次实验过程中在各测试函数上的平均收敛曲线(图 3)。在绝大多数测试函数上的对比实验,MSSOA所优化的结果最优、收敛曲线下降速度最快且较少出现收敛曲线停滞现象。具体而言,对于单峰函数F1-F5,MSSOA在优化F1-F4函数时,不仅达到了理论最优,而且收敛曲线的下降速度最快;对于函数F5,虽然MSSOA没有达到理论最优,但是其寻优精度最高,收敛曲线的下降速度最快。对于多峰函数F6-F9,MSSOA在函数F7和F8上以极快的速度收敛并且收敛精度要明显优于其他6种算法,甚至在优化F6、F9时,在寻优初期就已经收敛于理论最优值;对于固定维度函数F10-F12,在函数F12上,虽然MSSOA的收敛速度略慢于GWO等算法,但是MSSOA的寻优精度要明显优于GWO等算法,在优化函数F10和F11时,MSSOA以最快的收敛速度收敛于理论最优值。在测试函数F11、F12的收敛曲线中,曲线多次出现拐点,算法稍微出现停滞,但是以极少的迭代次数快速跳出局部最优,说明算法跳出局部最优的能力显著提高。上述结果表明,相较于其他算法,MSSOA在绝大多数函数上有更快的收敛速度、更高的收敛精度以及更强的跳出局部最优能力。
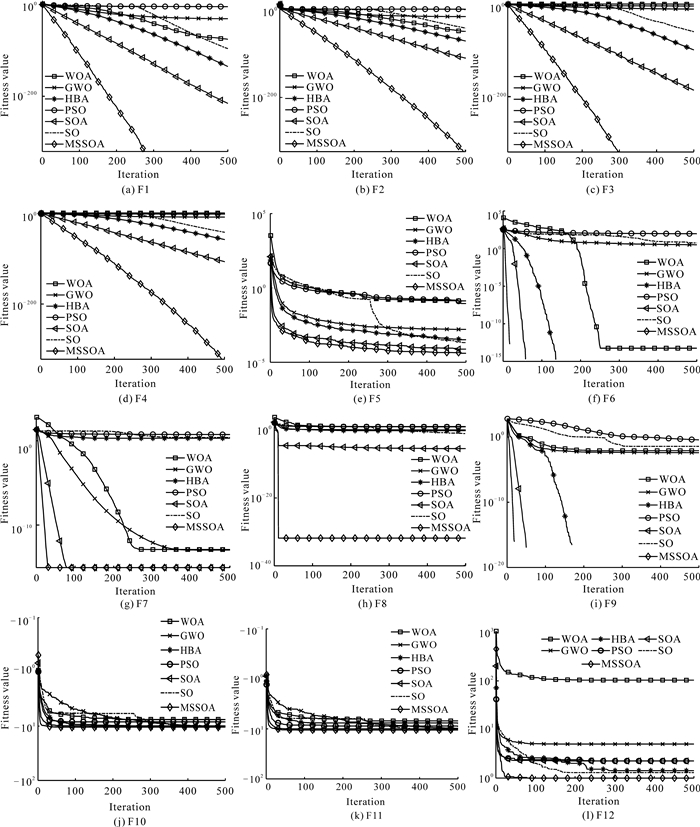
|
| 图 3 测试函数平均收敛曲线 Fig. 3 Average convergence curve of test function |
3.1.3 Wilcoxon秩和检验
Wilcoxon秩和检验用于验证不同算法运算结果的差异在统计学上的显著性,检验结果P值小于0.05说明两种算法寻优结果差异显著,否则说明两种算法寻优结果在整体上差异不显著[18],对于算法之间寻优结果差异不显著的用NaN表示,说明两者性能相当。为了进一步评估改进策略的有效性,本研究通过Wilcoxon秩和检验来验证MSSOA与其他算法的寻优结果有显著差异,以及所提的MSSOA有较强的寻优能力(表 4)。
| 函数 Function |
MSSOA vs WOA | MSSOA vs GWO | MSSOA vs HBA | MSSOA vs PSO | MSSOA vs SOA | MSSOA vs SO |
| F1 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 |
| F2 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 |
| F3 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 |
| F4 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 |
| F5 | 7.39E-11 | 3.02E-11 | 1.55E-09 | 3.02E-11 | 3.85E-03 | 3.02E-11 |
| F6 | 3.34E-01 | 1.19E-12 | NaN | 1.21E-12 | NaN | 5.85E-09 |
| F7 | 1.09E-08 | 1.15E-12 | 8.15E-02 | 1.21E-12 | NaN | 1.21E-12 |
| F8 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 1.21E-12 | 4.19E-02 | 1.21E-12 |
| F9 | 3.42E-01 | 8.06E-02 | NaN | 8.01E-09 | NaN | 8.06E-02 |
| F10 | 6.80E-08 | 6.80E-08 | 9.06E-07 | 3.01E-04 | 5.87E-06 | 1.07E-01 |
| F11 | 6.80E-08 | 6.80E-08 | 2.84E-01 | 6.92E-03 | 1.38E-06 | 2.85E-04 |
| F12 | 1.82E-11 | 1.82E-11 | 9.41E-01 | 1.89E-05 | 5.57E-11 | 1.82E-11 |
MSSOA在F6、F7以及F9上与HBA和SOA的差异不明显,主要是因为HBA和SOA在F6、F7以及F9上也基本达到了理论最优。但是从整体上来看,Wilcoxon秩和检验的P值大多小于0.05,MSSOA的运算结果与其他6种算法之间的差异显著,这进一步说明了MSSOA有较强的寻优能力。
3.2 工程应用结果对比分析 3.2.1 拉伸/压缩弹簧优化问题为了验证MSSOA的实际应用能力,通过拉伸/压缩弹簧设计优化问题来测试算法在有约束条件下解决实际问题的能力。为保证公平性,各算法参数、实验次数、最大迭代次数、种群个数等均同表 2。本节采用惩罚函数来处理不等式,具体为对不满足约束条件的解进行惩罚,将惩罚变量作为函数的一部分,则目标函数对应的罚函数Jaug(x)如式(15)所示:
| $ J_{\text {aug }}(x)=f(x)+\alpha \sum\limits_{i=1}^n\left[\max \left(0, b_i(x)\right)\right], $ | (15) |
其中,α为惩罚变量,取值为1 000;f(x)为原始的目标函数;n为约束条件的个数;bi(x)为第i个约束条件。
拉伸/压缩弹簧设计优化问题是一个经典有约束条件的工程优化问题,该问题要求在满足3个设计变量的4个约束条件的情况下求得弹簧重量的最小值[19],其数学表达式如式(16)所示。
目标函数:
约束条件:
| $ \begin{array}{l} g_2(x)=\frac{4 x_2^2-x_1 x_2}{12566\left(x_2 x_1^3-x_1^4\right)}+\frac{1}{5108 x_1^2}-1 \leqslant 0, \\ g_3(x)=1-\frac{140.45 x_1}{x_2^2 x_3} \leqslant 0, \\ g_4(x)=\frac{x_1+x_2}{1.5}-1 \leqslant 0 。\end{array} $ |
取值范围:
| $ 0.05 \leqslant x_1 \leqslant 2.00, 0.25 \leqslant x_2 \leqslant 1.30, 2 \leqslant x_3 \leqslant 15 \text { 。} $ | (16) |
7种算法对该问题的优化结果见表 5,可以看出MSSOA寻优结果的精确度要优于其他6种算法,这是由于MSSOA相较于对比算法有着更强的全局搜索能力和局部搜寻能力,能够搜寻到更多更高质量的解,因此能够取得更优的优化结果。拉伸/压缩弹簧设计优化问题结果说明MSSOA在工程实际应用中有很强的竞争力,也更加证明MSSOA的寻优能力强。
| 算法 Algorithm |
x1 | x2 | x3 | 最优值 Optimum value |
| WOA | 0.052 618 | 0.379 477 | 10.069 72 | 0.012 681 |
| GWO | 0.051 984 | 0.363 460 | 10.937 65 | 0.012 707 |
| HBA | 0.052 138 | 0.367 622 | 10.677 18 | 0.012 669 |
| PSO | 0.051 711 | 0.357 217 | 11.262 19 | 0.012 668 |
| SOA | 0.051 537 | 0.353 037 | 11.509 50 | 0.012 668 |
| SO | 0.051 243 | 0.346 091 | 11.940 29 | 0.012 783 |
| MSSOA | 0.051 882 | 0.361 374 | 11.021 13 | 0.012 666 |
| Note: bold fonts represent the best results in the experiment. | ||||
3.2.2 并联冷机负荷分配问题
中央空调冷机系统由两台或两台以上的冷水机组组成,在并联多冷机系统中,每台冷水机组根据末端负荷的需求来调整自身的负荷大小,以提供需要的制冷量。在满足末端负荷需求的同时,消耗的总功率越小,系统的整体性能越强。冷水机组的功率与其部分荷载率(Partial Load Rate,PLR)有关,功率与部分荷载可拟合为如式(17)的多项式[20]:
| $ P_i=a_i+b_i \mathrm{PLR}_i+c_i \mathrm{PLR}_i^2+d_i \mathrm{PLR}_i^3, $ | (17) |
其中,Pi为第i台冷机的功耗,PLRi为第i台冷机的部分荷载率,ai、bi、ci和di为冷水机组的性能系数。
为充分满足冷机性能,冷机部分荷载率不应该小于0.3,因此并联冷机系统负荷分配问题的数学模型如式(18)所示:
| $ \begin{array}{l} \min P_{\text {total }}=\min \left(\sum\limits_{i=1}^n P_i\right) \\ \text { s. t. } 0.3 \leqslant \mathrm{PLR}_i \leqslant 1 \text { 或 } \mathrm{PLR}_i=0 \;\;\text {, } \\ \sum\limits_{i=1}^n \mathrm{PLR}_i * Q_i=Q_{\text {need }}, i=1, 2, \cdots, n \end{array} $ | (18) |
其中,Ptotal为总功耗,n为冷水机组的台数,Qi为第i台机组的额定制冷量,Qneed为末端负荷需求。
为了验证MSSOA对于解决并联冷机负荷分配问题的能力,选取文献[21]的案例进行优化测试。该并联机组中,共有4台冷水机组,其中两台的额定制冷量为1 582.65 kW,另外两台的额定制冷量为3 517.00 kW。表 6为每台冷机能耗模型的相关系数以及额定制冷量,表 7为MSSOA与标准SOA、GA[21]、NCS[22]、IWOA[23]优化并联冷水机组性能的结果。
| i | a | b | c | d | Q/kW |
| 1 | 104.09 | 166.57 | -430.13 | 512.53 | 1 582.65 |
| 2 | -67.15 | 1 177.79 | -2 174.53 | 1 456.53 | 1 582.65 |
| 3 | 384.71 | -779.13 | 1 151.42 | -63.20 | 3 517.00 |
| 4 | 541.63 | 413.48 | -3 626.50 | 4 021.40 | 3 517.00 |
| Qneed/kW | 算法 Algorithm |
PLR1 | PLR2 | PLR3 | PLR4 | Ptotal/kW |
| 9 179.37 (90%) |
GA | 0.992 5 | 0.948 7 | 1.000 0 | 0.736 6 | 1 862.18 |
| NCS | 0.950 0 | 0.920 0 | 0.980 0 | 0.770 0 | 1 857.00 | |
| IWOA | 0.997 2 | 0.899 6 | 1.000 0 | 0.756 5 | 1 857.71 | |
| SOA | 0.965 2 | 0.958 5 | 1.000 0 | 0.757 8 | 1 858.08 | |
| MSSOA | 0.982 5 | 0.915 3 | 1.000 0 | 0.756 0 | 1 856.69 | |
| 8 159.44 (80%) |
GA | 0.861 1 | 0.813 2 | 0.880 9 | 0.685 9 | 1 457.23 |
| NCS | 0.800 0 | 0.760 0 | 0.920 0 | 0.680 0 | 1 456.00 | |
| IWOA | 0.828 1 | 0.805 6 | 0.902 3 | 0.682 6 | 1 455.83 | |
| SOA | 0.843 6 | 0.785 5 | 0.903 4 | 0.683 5 | 1 455.89 | |
| MSSOA | 0.806 2 | 0.797 3 | 0.911 8 | 0.686 6 | 1 455.78 | |
| 7 139.51 (70%) |
GA | 0.659 2 | 0.760 5 | 0.755 7 | 0.636 0 | 1 183.80 |
| NCS | 0.710 0 | 0.700 0 | 0.720 0 | 0.660 0 | 1 180.00 | |
| IWOA | 0.735 7 | 0.737 3 | 0.722 3 | 0.644 8 | 1 178.27 | |
| SOA | 0.690 3 | 0.714 4 | 0.754 9 | 0.643 0 | 1 180.42 | |
| MSSOA | 0.724 1 | 0.749 4 | 0.717 9 | 0.649 0 | 1 177.68 | |
| 6 119.58 (60%) |
GA | 0.595 6 | 0.698 2 | 0.571 0 | 0.587 4 | 1 001.62 |
| NCS | 0.620 0 | 0.690 0 | 0.550 0 | 0.590 0 | 999.00 | |
| IWOA | 0.588 7 | 0.671 1 | 0.564 6 | 0.608 5 | 998.77 | |
| SOA | 0.643 3 | 0.644 8 | 0.552 0 | 0.608 4 | 999.22 | |
| MSSOA | 0.591 6 | 0.665 9 | 0.562 1 | 0.612 0 | 998.28 | |
| 5 099.65 (50%) |
GA | 0.596 2 | 0.363 6 | 0.442 3 | 0.575 8 | 907.72 |
| NCS | 0.460 0 | 0.420 0 | 0.460 0 | 0.580 0 | 901.00 | |
| IWOA | 0.605 8 | 0.000 0 | 0.567 4 | 0.610 0 | 752.93 | |
| SOA | 0.676 1 | 0.000 0 | 0.543 4 | 0.602 4 | 756.31 | |
| MSSOA | 0.605 5 | 0.000 0 | 0.569 0 | 0.608 5 | 752.92 | |
| 4 079.72 (40%) |
GA | 0.332 5 | 0.315 7 | 0.324 6 | 0.543 6 | 856.30 |
| NCS | 0.540 0 | 0.640 0 | 0.000 0 | 0.630 0 | 688.00 | |
| IWOA | 0.000 0 | 0.000 0 | 0.555 1 | 0.604 9 | 688.01 | |
| SOA | 0.359 8 | 0.000 0 | 0.442 4 | 0.556 0 | 666.61 | |
| MSSOA | 0.398 4 | 0.000 0 | 0.418 2 | 0.562 6 | 665.57 | |
| Note: bold fonts represent the best results in the experiment. | ||||||
MSSOA相较于GA、NCS、IWOA、SOA在不同的负荷需求下均能取得节能效果。相较于GA,MSSOA所优化的结果能够节能0.10%-22.27%,节能效率具有较大的提升,MSSOA相较于NCS、IWOA以及标准SOA,在不同负荷需求下最高分别能够实现16.44%、3.26%和0.45%的节能效果。MSSOA相较于对比算法,其节能效果得到提升,这归功于佳点集策略能够增强种群个体的遍历能力,使得种群个体能够搜索到更多局部最优解,惯性权重策略以及t-分布扰动策略提高MSSOA的全局搜索和局部搜寻能力,使MSSOA搜索到高质量的解的能力显著提高。并联冷机负荷分配优化结果说明MSSOA在处理优化并联冷机负荷分配问题上有一定的优势,同时也展示出MSSOA具有很强的全局搜索和局部搜寻能力。
4 结论针对传统技能优化算法中在初始化、收敛性及寻优精度方面的不足,本研究提出一种多策略集成改进的技能优化算法MSSOA,采用佳点集、自适应权重及t-分布扰动等集成策略,解决随机初始化产生的种群个体的盲目性和不均匀的问题,保证种群的遍历性,加快算法收敛速度,同时提高算法的全局搜索能力以及减少个体陷入局部最优的概率。实验结果表明MSSOA具有收敛速度快、寻优精度高、鲁棒性强等特点,性能明显优于对比算法,在解决复杂问题上具有很强的竞争力。虽然MSSOA有很强的整体性能,但是MSSOA在测试部分函数时表现不佳,如何改进这些缺点,并将MSSOA拓展应用到其他领域将是未来重点研究的方向。
| [1] |
GIVI H, HUBÁLOVSKÁ M. Skill optimization algorithm: a new human-based metaheuristic technique[J]. Computers Materials & Continua, 2023, 75(1): 179-202. |
| [2] |
FATHY A, REZK H, FERAHTIA S, et al. A new fractional-order load frequency control for multi-renewable energy interconnected plants using skill optimization algorithm[J]. Sustainability, 2022, 14(22): 14999. DOI:10.3390/su142214999 |
| [3] |
石建平, 刘国平, 李培生, 等. 双策略协同进化果蝇优化算法及其应用[J]. 计算机集成制造系统, 2022, 28(5): 1482-1495. |
| [4] |
WANG Y, ZHANG X, YU D J, et al. Tent chaotic map and population classification evolution strategy-based dragonfly algorithm for global optimization[J]. Mathematical Problems in Engineering, 2022, 2022: 2508414. |
| [5] |
HE Z X, PAN Y H, WANG K J, et al. Area optimization for MPRM logic circuits based on improved multiple disturbances fireworks algorithm[J]. Applied Mathematics and Computation, 2021, 399: 126008. DOI:10.1016/j.amc.2021.126008 |
| [6] |
郑洪清, 冯文健, 周永权. 融合正弦余弦算法的蝴蝶优化算法[J]. 广西科学, 2021, 28(2): 152-159. |
| [7] |
MA S D, FANG Y M, ZHAO X D, et al. Multi-swarm improved grey wolf optimizer with double adaptive weights and dimension learning for global optimization problems[J]. Mathematics and Computers in Simulation, 2023, 205: 619-641. DOI:10.1016/j.matcom.2022.10.007 |
| [8] |
SONG S M, WANG P J, HEIDARI A A, et al. Dimension decided Harris hawks optimization with Gaussian mutation: balance analysis and diversity patterns[J]. Knowledge-Based Systems, 2021, 215: 106425. DOI:10.1016/j.knosys.2020.106425 |
| [9] |
宁杰琼, 何庆. t-分布扰动策略和变异策略的花授粉算法[J]. 小型微型计算机系统, 2021, 42(1): 64-70. |
| [10] |
林玲, 陈福集, 谢加良, 等. 基于改进灰狼优化支持向量回归的网络舆情预测[J]. 系统工程理论与实践, 2022, 42(2): 487-498. |
| [11] |
LAN K T, LAN C H. Notes on the distinction of Gaussian and Cauchy mutations[C]//2008 Eighth International Conference on Intelligent Systems Design and Applications. Piscataway, NJ, USA: IEEE, 2008: 272-277.
|
| [12] |
王娟, 秦江涛. 混沌映射与t-分布变异策略改进的海鸥优化算法[J]. 计算机应用研究, 2022, 39(1): 170-176, 182. |
| [13] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Piscataway, NJ, USA: IEEE, 1995: 1942-1948.
|
| [14] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [15] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [16] |
HASHIM F A, HOUSSEIN E H, HUSSAIN K, et al. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems[J]. Mathematics and Computers in Simulation, 2022, 192: 84-110. |
| [17] |
HASHIM F A, HUSSIEN A G. Snake optimizer: a novel meta-heuristic optimization algorithm[J]. Knowledge-based Systems, 2022, 242: 108320. |
| [18] |
DERRAC J, GARCÍA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18. |
| [19] |
张阳, 周溪召. 求解全局优化问题的改进灰狼算法[J]. 上海理工大学学报, 2021, 43(1): 73-82. |
| [20] |
于军琪, 陈时羽, 赵安军, 等. 改进交替方向乘子法求解冷水机组负荷分配群智能优化问题[J]. 控制理论与应用, 2021, 38(7): 947-962. |
| [21] |
CHANG Y C, LIN J K, CHUANG M H. Optimal chiller loading by genetic algorithm for reducing energy consumption[J]. Energy and Buildings, 2005, 37(2): 147-155. |
| [22] |
童瑞祺, 丁强, 江爱朋. 基于改进布谷鸟搜索算法的冷水机组负荷分配优化[J]. 计算机与应用化学, 2019, 36(4): 397-403. |
| [23] |
冯增喜, 李嘉乐, 葛珣, 等. 融合多策略改进鲸鱼优化算法及其应用[J/OL]. 计算机集成制造系统, 2023: 1-23(2023-01-05)[2023-03-07]. http://kns.cnki.net/kcms/detail/11.5946.tp.20230104.1215.014.html.
|



