2. 广西警察学院信息技术学院, 广西南宁 530028;
3. 中国人民公安大学研究生院, 北京 100038
2. School of Information Technology, Guangxi Police College, Nanning, Guangxi, 530028, China;
3. Graduate School, People's Public Security University of China, Beijing, 100038, China
随着图结构数据在社交网络[1]、犯罪网络[2]以及知识图谱[3]等领域的广泛应用,构建高性能图数据分析和挖掘算法,提取数据中蕴含的有效高维非线性特征已成为当前研究的重点内容。传统基于启发式的图分析算法[4]受限于人工设计特征和对数据分布的强假设等问题,不仅具有较高的计算复杂度,而且泛化能力也较弱。基于深度学习的图表示学习算法[5]因其强大的表征能力,受到了越来越多的关注。图表示学习将节点编码为一组保留拓扑结构信息、节点属性信息等原始图信息的低维向量,进而提升节点分类、节点聚类、链接预测以及可视化等下游图分析任务的正确率与效率。
图表示学习的关键在于选择和编码原始图特征,从而生成低维的节点表示向量。由于图数据中包含局部拓扑结构、全局拓扑结构以及节点属性等多种不同类型信息,增加了特征选择的难度,因此多数图表示学习模型依赖具体的图分析任务来保留特征,例如节点分类关注模型对节点间相似性和差异性的保留能力,链接预测关注模型对节点间局部拓扑结构的保持和推断能力。当前,对图表示学习算法的改进方式主要分为两类,一是设计不同的神经网络结构,二是改进模型优化方式和策略。神经网络结构的设计可以通过修改图卷积编码器[6]以增强模型对原始图特征的提取能力;也可以通过在多层神经网络中引入残差连接[7]、One-Shot聚合[8]等跨层连接方式,改善层间信息传递;还可以通过多视角[9]、多尺度[10]等形式,从不同角度关注和保留原始图信息。优化方式和策略的改进可以通过引入不同的损失函数以保留相应的拓扑或属性信息;也可以通过噪声注入[11]、对抗训练[12]等方式增强模型的泛化能力。
变分图自编码器(Variational Graph Auto Encoder, VGAE)[13]是一类重要的图表示学习算法,由变分自编码器(Variational Auto Encoder, VAE)[14]构建,编码器部分利用图卷积生成用于计算节点表示的概率分布,解码器部分利用节点表示重构邻接关系,实现链接预测任务。在VGAE的基础上衍生出许多变体,Salha等[15]提出了一种线性变分自编码器模型Linear-VGAE,其使用线性编码的简化图卷积(Simplified Graph Convolution, SGC)[16]替换VGAE中的图卷积编码器,减少模型的参数规模并降低计算复杂度,实现链接预测和节点聚类任务;Keser等[17]使用残差连接构建残差变分图自编码器(Residual Variational Graph Auto Encoder, RVGAE),通过计算机视觉中常用的跨层连接方式改善层间信息传递,实现链接预测任务;Hy等[10]提出了一种多尺度变分图自编码器(Multi-Scale Variational Graph Auto Encoder, MSVAGE),通过编码器生成多组不同尺度的低维向量表示原始图的混合概率分布,然后在每个维度上进行多次采样,并通过属性信息帮助结构表征学习,实现链路预测任务。
虽然上述改进方式提升了VGAE及其变体模型的性能,但是多数模型仅针对特定的图分析任务进行优化,即依赖具体任务进行特征保留,因此限制了模型生成的节点表示在不同图分析任务上的表现。针对上述问题,本文提出一种基于自监督信息[18]增强的图表示学习模型Self-VGAE,以生成适用于多个图分析任务的泛化节点表示。Self-VGAE主要分为两个部分:一是使用双层图卷积编码器和节点表示内积解码器构建基础VGAE模型,并通过重构损失和噪声约束对基础VGAE模型进行训练;二是使用拓扑结构和节点属性构建自监督信息,并在模型训练过程中利用构建的自监督信息约束节点表示的生成。
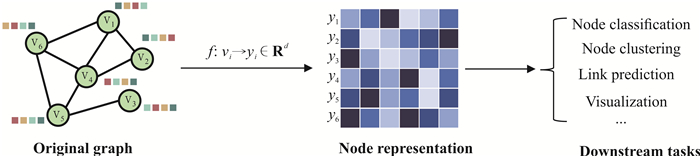
1 相关工作 1.1 图表示学习开发高效的图结构分析算法已成为现在的研究热点。由于传统的路径分析、连通性分析和中心性分析等启发式算法从邻接矩阵中提取图的拓扑信息时依赖人工设计的特征,因此在应用时受限于数据的高维非线性,通常具有较高的计算复杂度和内存需求,并且人工设计的特征通常针对特定任务,在不同任务中的泛化能力十分有限[4]。图表示学习算法通过映射函数将原始图的拓扑结构和属性信息编码到潜在向量空间中,使高维、稀疏的图数据转换为低维、稠密的向量,在最大限度保留图特征信息的同时,解决图结构难以高效输入机器学习算法中的问题。图表示学习算法的一般过程如图 1所示。
|
| 图 1 图表示学习算法的一般过程 Fig. 1 Process of graph representation learning algorithms |
近年来,许多学者通过修改模型优化方式和策略来提升图表示学习算法的性能。Wang等[11]提出基于噪声注入的训练策略,通过将噪声注入到输入图中,在防止模型参数过拟合的同时,设置合适的噪声率能够持续提高训练性能。Wang等[19]提出能够同时提取节点属性和拓扑结构信息的图卷积自编码器模型GASN,利用节点属性和拓扑星系重构损失,从而对编码和解码过程进行优化,增强模型对原始图信息的表征能力。Fettal等[20]将聚类损失函数纳入表示学习过程,最小化节点表示与重建聚类表示之间的差异,提升模型在聚类任务中的表现。Li等[21]利用对抗互信息训练模型,在VAE编码过程中最大化节点特征和节点表示的互信息,使模型能够有效保留图的拓扑结构和节点属性信息。
1.2 自监督学习自监督学习[22]是从无监督数据中提取可转移的知识或特性,将其扩展为自监督信息,并利用自监督信息对神经网络进行训练,最终生成对下游任务有价值的特征表示。当前,主流的自监督学习算法主要分为预测模型和对比模型[22]。预测模型采用监督学习方式进行训练,利用输入数据生成自监督标签,对预测结果和自监督标签之间的差异进行优化;对比模型则采用自监督学习方式生成数据表示,利用输入数据构造正负样本对,增大特征空间中同类数据表示的相似性和不同类数据表示的差异性。
由于图表示学习算法通常采用无监督学习方式进行训练,因此难以运用预测模型生成的自监督标签对特征提取过程进行约束。对比模型能够调整正负样本对的距离,因此可以将其融入到图表示学习的训练过程。对比模型的关键在于如何从输入数据中提取包含正向和负向关系的自监督信息,并构建对比约束对正负样本距离进行度量。在自监督学习中,对比约束的一般形式为
| $ \begin{array}{l} \;\;\;\;\;\;\;\operatorname{loss}\left(x_i\right)= \\ -\log \frac{\exp \left(s_{i, i} / \tau\right)}{\sum\nolimits_{k=1}^N 1_{[k \neq i]} \exp \left(s_{i, k}\right)+\exp \left(s_{i, i} / \tau\right)}, \end{array} $ | (1) |
式中, τ为对比约束中的温度系数,用于控制模型对负样本的关注度,s为数据样本相似性度量的结果。式(1)也被称为InfoNCE[23],对比约束可以使第i个数据与正样本之间的相似度si, i尽可能大,与负样本之间的相似度si, k尽可能小。Hu等[24]使用图的拓扑结构生成自监督信息,然后使用InfoNCE构建局部结构对比约束,使仅使用节点属性作为输入的多层感知模型能够匹配图卷积神经网络(Graph Convolutional Network, GCN)[6]在节点分类任务中的性能。
本文在上述研究的基础上,使用原始图的节点属性和拓扑结构生成自监督信息,并基于InfoNCE设计用于图表示学习任务的自监督约束,以推动特征空间相似节点表示相互接近,不相似节点表示相互远离,在增强模型对原始图信息表征能力的同时,提升模型在节点分类、节点聚类、链接预测等多个下游图分析任务的表现。
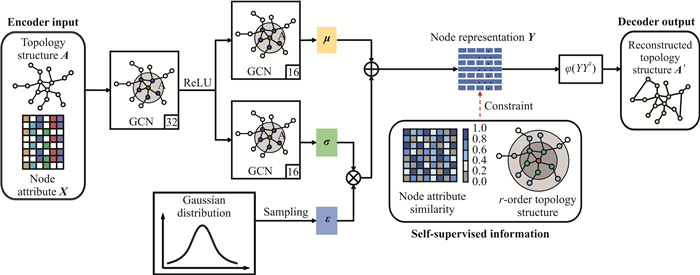
2 图表示学习模型(Self-VGAE)Self-VGAE的算法原理如图 2所示,首先给出VGAE模型的编解码器网络结构以及优化函数,用于提取原始图特征并生成节点向量表示,然后在VGAE的基础上引入增强模型表征能力的自监督损失,对节点表示进行优化,使潜在空间中相似节点彼此接近,不相似节点彼此远离。
|
| 图 2 Self-VGAE的结构 Fig. 2 Framework of Self-VGAE |
2.1 图变分自编码器
VGAE使用GCN编码器对原始图进行特征提取,以生成用于计算节点表示的均值向量μ和方差向量σ。具体而言,GCN以蕴含拓扑结构信息的邻接矩阵A和蕴含节点属性信息的属性矩阵X为输入,其层间传播公式为
| $ \boldsymbol{H}^{(l+1)}=\delta\left(\tilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{H}^{(l)} \boldsymbol{W}^{(l+1)}\right), $ | (2) |
式中,
Self-VGAE模型基本结构与VGAE相同,编码器使用双层GCN进行编码,第一层表达式为
| $ \boldsymbol{H}^{(1)}=\operatorname{ReLU}\left(\tilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{X} \boldsymbol{W}^{(1)}\right) 。$ | (3) |
然后基于第一层计算结果生成 μ和σ,第二层表达式为
| $ \begin{array}{l} \boldsymbol{\mu}=\widetilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \widetilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{H}^{(1)} \boldsymbol{W}^{(\boldsymbol{\mu})} \\ \ln \boldsymbol{\sigma}=\widetilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{H}^{(1)} \boldsymbol{W}^{(\boldsymbol{\sigma})}, \end{array} $ | (4) |
式中,W(μ)和W(σ)分别表示用于计算μ和σ的参数矩阵。利用编码器计算的μ和σ以及从高斯分布中采样的噪声编码ε,计算节点表示矩阵Y:
| $ \boldsymbol{Y}=\boldsymbol{\mu}+\boldsymbol{\sigma} \odot \boldsymbol{\varepsilon}, $ | (5) |
式中,Y={yi}i=1N,yi是节点i的低维表示,N为节点数量,⊙表示Hadamard积运算。
对于Self-VGAE模型,解码器利用节点表示的内积生成重构邻接矩阵 A′:
| $ \boldsymbol{A}^{\prime}=\varphi\left(\boldsymbol{Y} \boldsymbol{Y}^{\mathrm{T}}\right), $ | (6) |
式中,φ为Sigmoid函数。与VAGE的模型优化方式相似,Self-VGAE在训练过程中也使用重构损失和噪声约束的概率形式进行优化,其表达式为
| $ \begin{array}{l} \;\;\;\;\;\;\;\operatorname{loss}_{\text {VGAE }}=\mathrm{E}_{q(\boldsymbol{Y}\mid\boldsymbol{X}, \boldsymbol{A})}[\ln p(\boldsymbol{A} \mid \boldsymbol{Y})]-\operatorname{KL}[q(\boldsymbol{Y} \mid \boldsymbol{X}, \\ \boldsymbol{A}) \| p(\boldsymbol{Y})], \end{array} $ | (7) |
式中,KL [q(·)||p(·)]为q(·)和p(·)的KL散度,p(Y)表示高斯先验:
| $ p(\boldsymbol{Y})=\prod\limits_i p\left(\boldsymbol{y}_i\right)=\prod\limits_i \mathcal{N}\left(\boldsymbol{y}_i \mid 0, \boldsymbol{I}\right) 。$ | (8) |
式中,
本节使用图的拓扑结构和节点属性信息生成自监督信息,并基于InfoNCE设计用于图表示学习模型训练的自监督约束。对于拓扑结构信息,通常使用邻接矩阵 A表示,例如节点i和j之间存在边则邻接矩阵元素Aij的值为1,节点i和j之间无边则Aij的值为0,并且无向图中Aij和Aji的值相同。可见,邻接矩阵本身就包含了正负关系,即有边节点作为正样本,无边节点作为负样本。因此,在生成拓扑自监督信息时,不仅可以使用邻接矩阵构建一阶邻域关系的正负样本,还可以构建高阶邻域关系的正负样本:
| $ \boldsymbol{\omega}^{\mathrm{T}}=\overline{\boldsymbol{A}}^r, $ | (9) |
式中,A表示归一化的邻接矩阵A,r表示 A的阶数,ωT表示节点间的r阶邻域关系:
| $ \omega_{i j}^{\mathrm{T}}\left\{\begin{array}{l} =0, \text { 节点 } j \text { 不是节点 } i \text { 的 } r \text { 阶邻居 } \\ \neq 0, \text { 节点 } j \text { 是节点 } i \text { 的 } r \text { 阶邻居 } \end{array}\right.\;\;\;\;\;\;\;\;\;。$ | (10) |
基于InfoNCE和 ωT构建拓扑对比约束lossT:
| $ \operatorname{loss}_{\mathrm{T}}=-\log \frac{\sum\nolimits_{j=1}^N \mathbf{1}_{[j \neq i]} \omega_{i j}^{\mathrm{T}} \exp \left(\operatorname{sim}\left(y_i, y_j\right)\right)}{\sum\nolimits_{k=1}^N \mathbf{1}_{[k \neq i]} \exp \left(\operatorname{sim}\left(y_i, y_k\right)\right)}, $ | (11) |
式中,sim表示相似度函数(本文使用余弦相似度)。拓扑对比约束将每个节点的r阶邻居作为正样本,其他节点为负样本,从而激励正样本向量表示接近目标节点,负样本向量表示远离目标节点。
对于节点属性信息,通常使用属性矩阵 X表示,例如节点i有属性j则属性矩阵元素 Xij的值为1,节点i没有属性j则属性矩阵元素 Xij的值为0。可见,属性矩阵表示的是节点与属性之间的关系,不能直接构建节点间的正负关系。因此,在生成属性自监督信息时,首先要对节点在属性空间的相似性进行度量:
| $ S_{i j}=\frac{\boldsymbol{x}_i \cdot \boldsymbol{x}_j}{\left|\boldsymbol{x}_j\right|\left|\boldsymbol{x}_j\right|}, $ | (12) |
式中,
| $ \boldsymbol{\omega}^{\mathrm{F}}=\overline{\boldsymbol{S}}^{(k)}, $ | (13) |
式中,S(k)表示归一化的属性相似度矩阵 S(k),ωF表示节点在属性空间的关系:
| $ \omega_{i j}^{\mathrm{F}}\left\{\begin{array}{l} =0, \text { 节点 } j \text { 与节点 } i \text { 无属性关联 } \\ \neq 0, \text { 节点 } j \text { 与节点 } i \text { 存在属性关联 } \end{array}\;\;\;\;\;\;\;\;\;\;\;。\right. $ | (14) |
基于InfoNCE和 ωF构建属性对比约束lossF:
| $ \begin{array}{l} \;\;\;\;\;\;\;\operatorname{loss}_{\mathrm{F}}= \\ -\log \frac{\sum\nolimits_{j=1}^N \mathbf{1}_{[j \neq i]} \omega_{i j}^{\mathrm{F}} \exp \left(\operatorname{sim}\left(y_i, y_j\right)\right)}{\sum\nolimits_{k=1}^N \mathbf{1}_{[k \neq i]} \exp \left(\operatorname{sim}\left(y_i, y_k\right)\right)} 。\end{array} $ | (15) |
属性对比约束将存在属性关联的节点作为正样本,其他节点为负样本,鼓励正样本向量表示接近目标节点,推动负样本向量表示远离目标节点。
在VGAE模型优化过程中,将lossVGAE与基于拓扑和属性信息构建的自监督约束lossT和lossF进行组合,构建完整的损失函数lossFinal:
| $ \operatorname{loss}_{\mathrm{Final}}=\operatorname{loss}_{\mathrm{VGAE}}+\alpha \operatorname{loss}_{\mathrm{T}}+\beta \operatorname{loss}_{\mathrm{F}}, $ | (16) |
式中,α和β是平衡自监督约束的加权系数。
3 结果与分析 3.1 数据集本文使用基准引文网络数据集Cora、Citeseer、Pubmed[25]评估基线模型和Self-VGAE在图分析任务中的实验表现。在数据集中,每个节点表示一篇论文,每条边表示不同论文间的引用关系,节点属性是论文内容的向量表示,节点标签表示论文的研究主题。数据集统计信息如表 1所示。
| 数据集 Datasets |
#节点 #Nodes |
#链接 #Edges |
#属性 #Attributes |
#标签 #Labels |
| Cora | 2 708 | 5 429 | 1 433 | 7 |
| Citeseer | 3 327 | 4 732 | 3 703 | 6 |
| Pubmed | 19 717 | 44 338 | 500 | 3 |
3.2 基线模型
本文使用VGAE及其较为先进的变体作为基线。
VGAE:以VAE为基础架构,编码器使用GCN生成节点表示的均值和方差向量,解码器使用节点特征表示的内积恢复邻接关系,训练过程中使用重构损失和KL散度对模型参数进行优化。
Linear-VGAE:在VGAE的基础上,使用线性编码的SGC代替GCN,并取消了层间激活函数,通过线性神经网络编码图信息,从而提升模型计算效率。
GC-VGAE[26]:在VGAE的基础上,对模型优化方式进行修改,在通过内积解码器恢复邻接矩阵的同时,引入与编码器对称的属性解码器,增强模型对拓扑结构和节点属性信息的保留。
MSVGAE:在VGAE的基础上,对模型编码过程进行修改,构造不同尺度的图信息,实现以多尺度和等变的方式学习特征表示,并通过图属性信息增强图结构的学习。
OSA-VGAE[8]:在VGAE的基础上,对编码器网络结构进行修改,通过One-Shot聚合改善多层GCN的信息传递,增强深层模型对原始图信息的表征能力。
3.3 评价指标在节点分类实验中,使用常见的分类指标Micro-F1和Macro-F1进行比较:
| $ \begin{array}{l} \text { Micro-F1 }=\frac{2 \times P \times R}{P+R}, \\ \text { Macro-F1 }=\frac{\sum\limits_{l \in L} \mathrm{~F} 1(l)}{|L|}, \end{array} $ | (17) |
式中,P表示精确率(Precision),R表示召回率(Recall),F1(l)是标签l的F1分数。Micro-F1在计算过程中考虑了每个类别中节点的数量,适用于数据分布不平衡的情况; 而Macro-F1计算过程中没有考虑节点数量差异,而是平等地看待每一类,受高P值和高R值类的影响较大。
在节点聚类实验中,采用归一化互信息(Normalized Mutual Information, NMI)评估模型性能:
| $ \begin{array}{l} \;\;\;\;\;\;\mathrm{NMI}= \\ 1-\frac{H\left(M_1 \mid M_2\right)_{\text {norm }}+H\left(M_2 \mid M_1\right)_{\text {norm }}}{2}, \end{array} $ | (18) |
式中,H(·)表示信息熵。NMI用于度量M1和M2聚类结果之间的相似性,值越大表明和真实结果共享的信息越多,聚类效果越好。
在链接预测中,对节点之间的边和非边进行预测,因此采用ROC曲线下面积(Area Under the ROC, AUC)和平均精度(Average Precision, AP)进行评估。AUC同时考虑了分类器对于正例和负例的分类能力,把阈值设置在紧靠每个正例之下,计算负类的查全率后再取平均值,能够在样本不平衡的情况下对分类器做出合理的评价。AP是把阈值设置在紧靠每个正例之下,计算正类的查准率后再取平均值,能够衡量模型在每个类别上的分类性能。
3.4 实验设置为保证公平性,所有基线模型及Self-VGAE均参照VGAE原文中设置的参数进行初始化,编码器隐藏层维度设置为32,VAE的均值和方差向量维度为16,训练过程中使用Adam优化器更新模型参数,学习率lr设为0.01,迭代次数n设为200。此外,Self-VGAE的邻接矩阵阶数r在{1, 5, 10, 15, 20}中搜索,属性相似邻居数k在{1, 5, 10, 15, 20}中搜索,自监督约束系数α和β在{0.05, 0.10, 0.15, 0.25, 0.50, 1.00}中搜索。综合节点分类、节点聚类和链接预测3个任务中的实验表现,Self-VGAE的参数设置如表 2所示。
| 数据集 Datasets |
lr | n | r | k | α | β |
| Cora | 0.01 | 200 | 1 | 10 | 0.10 | 0.10 |
| Citeseer | 0.01 | 200 | 2 | 10 | 0.10 | 0.10 |
| Pubmed | 0.01 | 200 | 1 | 15 | 0.10 | 0.15 |
3.5 节点分类
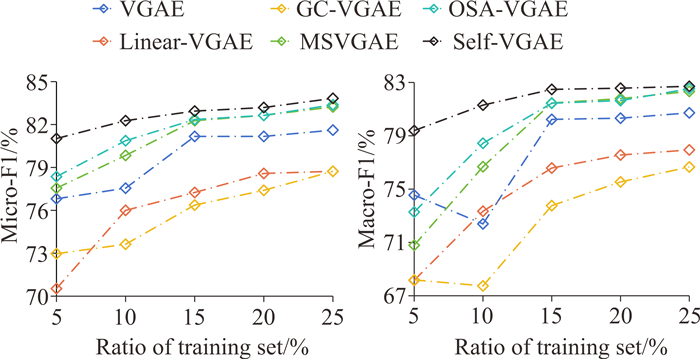
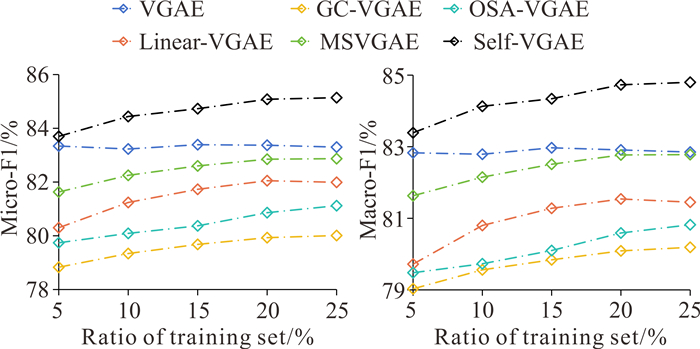
本节通过节点分类任务评估模型性能,将各模型生成的低维节点表示作为支持向量机的输入,以5%的间隔随机抽取5%-25%的标签作为训练集,剩余节点中随机抽取50%的标签作为测试集,各模型采用相同的数据集划分,记录Micro-F1和Macro-F1。实验结果如图 3至图 5所示。
|
| 图 3 节点分类实验结果(Cora) Fig. 3 Results of node classification experiment (Cora) |
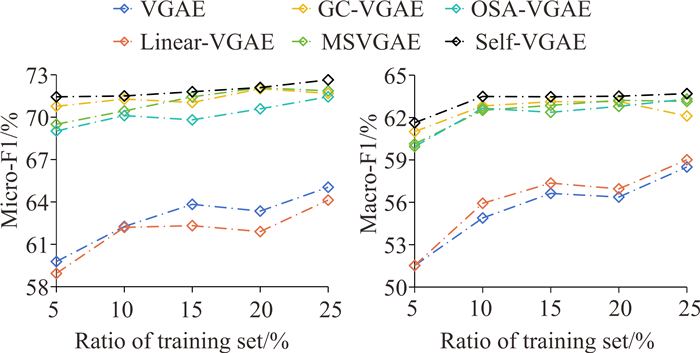
|
| 图 4 节点分类实验结果(Citeseer) Fig. 4 Results of node classification experiment (Citeseer) |
|
| 图 5 节点分类实验结果(Pubmed) Fig. 5 Results of node classification experiment (Pubmed) |
在3个数据集上,Self-VGAE的Micro-F1和Macro-F1曲线始终高于基线模型,表明基于拓扑结构和节点属性构建的自监督信息能够增强模型对原始图特征信息的表征能力,使生成的低维表示中保留了丰富的节点相似性和差异性信息,进而提升节点分类任务的实验表现。基线模型中,Linear-VGAE线性编码方式虽然降低了计算复杂度,但是在无监督条件下未能有效提取原始图的结构和属性信息,多数情况下实验表现弱于使用GCN编码器的VGAE;GC-VGAE通过恢复邻接矩阵和属性矩阵的方式保留原始图相关信息,但是在优化过程中缺少对拓扑和属性信息的平衡,使模型在不同数据集上的分类表现差异较大;保留多尺度拓扑结构信息的MSVGAE表现较为稳定,但仅从结构角度设计的表征方法忽略了属性信息的提取,限制了模型的分类性能。
在不同数据集上,同一基线分类结果差异较大。例如OSA-VGAE在Cora和Citeseer上表现出色,但是在Pubmed上表现较差。与基线模型不同,Self-VGAE在3个数据集上均取得了最佳的实验结果,反映出模型较为强大的泛化能力。此外,随着训练集中标签数量的增加,各模型分类结果总体呈上升趋势,但部分基线模型的改善不明显,例如VGAE在Pubmed数据集上的预测结果随标签数量增加未见提升,表明基线模型生成的节点表示在保留相似性和差异性信息上能力有限,不能随监督信息的增加提升模型的分类性能。相较基线模型,Self-VGAE能够充分利用拓扑结构和节点属性确定每个节点所属类别,仅使用5%的训练标签即可取得良好的表现(表 3),表明模型能够保留丰富的原始图信息,增大节点特征表示的可区分性。
| Unit: % | |||||||||||||||||||||||||||||
| 模型 Models |
Cora | Citeseer | Pubmed | ||||||||||||||||||||||||||
| Micro-F1 | Macro-F1 | Micro-F1 | Macro-F1 | Micro-F1 | Macro-F1 | ||||||||||||||||||||||||
| VGAE | 76.81 | 74.55 | 59.78 | 51.52 | 83.34 | 82.83 | |||||||||||||||||||||||
| Linear-VGAE | 70.53 | 68.16 | 58.94 | 51.53 | 80.30 | 79.72 | |||||||||||||||||||||||
| GC-VGAE | 72.97 | 68.19 | 70.77 | 61.00 | 78.83 | 79.03 | |||||||||||||||||||||||
| MSVGAE | 77.55 | 70.79 | 69.50 | 60.13 | 81.63 | 81.63 | |||||||||||||||||||||||
| OSA-VGAE | 78.36 | 73.28 | 69.02 | 59.95 | 79.74 | 79.48 | |||||||||||||||||||||||
| Self-VGAE | 81.02 | 79.39 | 71.44 | 61.63 | 83.70 | 83.39 | |||||||||||||||||||||||
| Note: bold is the best result, underlined is the second best result. | |||||||||||||||||||||||||||||
3.6 节点聚类
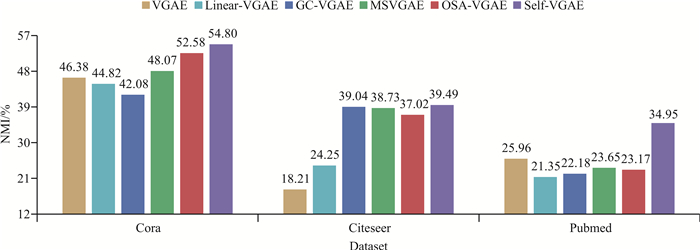
本节通过节点聚类任务评估模型性能,将各模型生成的低维节点表示作为K-means++算法的输入,实现无监督节点聚类,并记录NMI(图 6)。在K-means++算法中,K值设置为Cora、Citeseer和Pubmed数据集节点标签的类别数。
|
| 图 6 节点聚类实验结果 Fig. 6 Results of node clustering experiment |
在3个数据集上,Self-VGAE的NMI始终高于基线模型,表明基于拓扑结构和节点属性构建的自监督信息能够增强模型对社区结构拓扑信息的保留能力,使生成的低维表示中保留了丰富的有效社区信息,进而提升节点聚类任务的表现。基线模型中,Linear-VGAE的线性编码方式在无监督条件下未能有效提取图的高阶结构特征,在多数情况下实验表现弱于使用GCN编码的其他模型;GC-VGAE在优化过程中平等地计算重构拓扑结构和节点属性的损失函数,但缺少对社区结构等高阶拓扑信息的关注,因此限制了其在聚类任务中的实验表现;MSVAGE通过编码多组不同尺度的原始图信息,实现多尺度和等变特征学习,同时采用节点属性增强拓扑结构学习的策略,使模型在一定程度上保留了高阶结构特征,取得了较好的聚类表现。
在不同数据集上,多数基线模型的聚类结果差异较大,特别是OSA-VGAE模型在聚类任务中的实验表现与分类任务相同,Cora和Citeseer数据集上的实验表现优于原始的VGAE模型,但在Pubmed数据集上的实验表现较差,反映出该模型采用的信息传递方式对不同数据集的泛化能力有限。相反,MSVGAE和Self-VGAE能够保留更丰富的拓扑结构信息,在聚类任务中的实验表现更加稳定,特别是Self-VGAE通过自监督信息使同一社区内的节点在特征空间更加接近,因此在3个数据集上均获得了最佳的聚类表现。
3.7 链接预测通过链接预测任务评估模型实验性能。首先移除数据中20%的链接并随机采样20%的非链接(无链接节点对)构建测试集,然后使用剩余80%的链接进行训练,最后利用生成的节点表示内积重构邻接矩阵,对节点间是否存在链接关系进行预测,各模型采用相同的数据集划分,记录AUC和AP(表 4)。
| Unit: % | |||||||||||||||||||||||||||||
| 模型 Models |
Cora | Citeseer | Pubmed | ||||||||||||||||||||||||||
| AUC | AP | AUC | AP | AUC | AP | ||||||||||||||||||||||||
| VGAE | 89.60 | 90.87 | 90.46 | 91.90 | 92.60 | 93.21 | |||||||||||||||||||||||
| Linear-VGAE | 89.36 | 90.64 | 89.07 | 90.91 | 93.86 | 94.07 | |||||||||||||||||||||||
| GC-VGAE | 90.11 | 90.29 | 91.77 | 91.27 | 93.96 | 94.01 | |||||||||||||||||||||||
| MSVGAE | 91.93 | 91.97 | 93.66 | 93.79 | 92.05 | 92.21 | |||||||||||||||||||||||
| OSA-VGAE | 92.26 | 92.74 | 94.08 | 94.38 | 93.78 | 94.32 | |||||||||||||||||||||||
| Self-VGAE | 93.50 | 93.65 | 95.56 | 95.92 | 94.84 | 94.95 | |||||||||||||||||||||||
| Note: bold is the best result, underlined is the second best result. | |||||||||||||||||||||||||||||
在3个数据集上,Self-VGAE的AUC和AP始终高于基线模型,表明基于拓扑结构和节点属性构建的自监督信息能够增强模型对拓扑结构信息的保持和推断能力,使生成的低维表示中保留了丰富的邻域信息,进而提升链接预测任务的表现。基线模型中,Linear-VGAE以线性编码方式提取节点邻域关系的能力有限,在多数情况下弱于使用GCN编码的其他模型;GC-VGAE增加了对属性信息的保留,但节点表示中过多的属性信息对拓扑结构预测产生了一定负面影响,使模型在Cora和Citeseer两个数据集上的实验表现较差;MSVGAE使用的多尺度特征学习和属性增强策略在一定程度上增强了局部结构信息的保持能力,但模型仅在Cora和Citeseer数据集上表现较好,而在Pubmed数据集上表现较差,在链接预测任务中泛化能力有限;引入跨层信息传递策略的OSA-VGAE在节点分类和聚类任务中表现不佳,但是在链接预测任务中取得了较好的实验结果。
与基线模型相比,Self-VGAE在不同数据集上的链接预测任务中同样具有较强的泛化能力。此外,Self-VGAE和其他基线模型均由VGAE演化而来,区别在于采用不同的方式对模型进行改进。在3个数据集上,Self-VGAE在节点分类、节点聚类和链接预测任务中的实验结果相较VGAE均有较为明显的提升,不仅优于当前先进的基线模型,而且在不同任务中的表现也更加稳定,证明了自监督信息的引入能够增强模型对原始图信息的表征能力,使节点表示能够保留基于节点属性和拓扑结构相似性信息以及局部和高阶结构特征,进而提升下游图分析任务的实验表现。
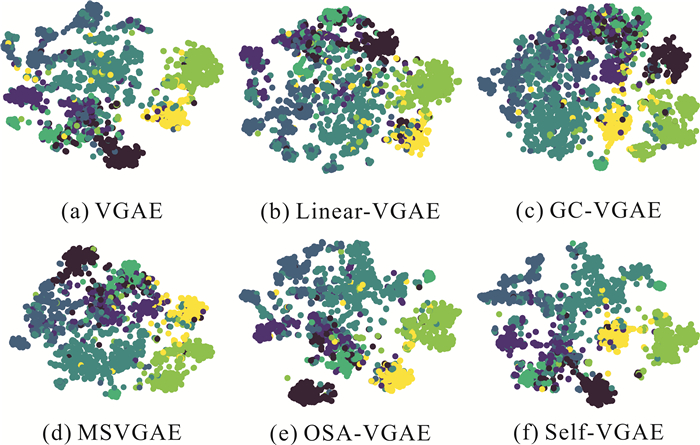
3.8 可视化节点特征表示蕴含了节点属性和拓扑结构信息,可视化后能直观地反映原始图的某些特征以及模型对原始图信息的表征能力。本节通过可视化任务对模型进行评估。首先使用t-SNE将基线和Self-VGAE模型在Cora数据集上生成的节点特征表示降至2维,然后根据节点标签将二维平面上的数据点标记为7种不同的颜色(图 7)。
|
| 图 7 节点表示可视化 Fig. 7 Visualization of node representations |
好的可视化结果通常相同颜色节点彼此接近,不同颜色节点彼此分离。由图 7可知,所有模型均能从任意分布的原始数据中提取相关信息并形成一定的社区结构,但是不同模型可视化结果的类内相似性和类间界限区别较大。其中,Linear-VGAE、GC-VGAE和MSVGAE的节点分布松散、类间差异不够明显,相反,VGAE、OSA-VGAE和Self-VGAE的类内节点分布更加接近,类间距离更远,特别是Self-VGAE在多个类别上均有较好的可视化效果。可视化实验直观反映了模型保留同一社群节点相似特征的能力,证明了自监督信息的引入增强了模型对原始图信息的表征能力,能够使同类节点表示在特征空间更加接近。
3.9 参数分析为了分析Self-VGAE性能受参数的影响,通过Cora和Citeseer数据集上的链接预测任务进行参数实验,并记录实验结果。相较学习率、迭代次数、嵌入维度等常见参数,本节仅对Self-VGAE特有参数邻接矩阵阶数r、属性相似邻居数k、自监督约束权重系数α和β进行验证。为了保证实验的公平性,除验证参数外,其余参数均按照表 2进行设置。
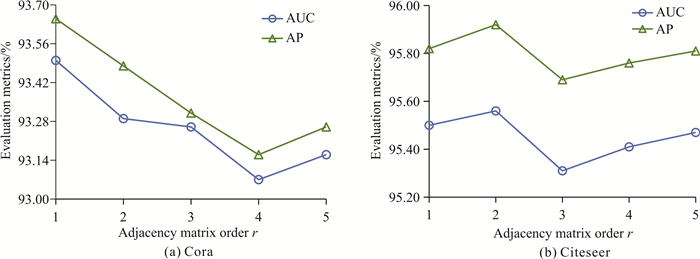
为了验证邻接矩阵阶数r对Self-VGAE性能的影响,使用不同的r值进行实验(图 8)。邻接矩阵阶数r与图的高阶结构特征相关,例如三阶邻接矩阵蕴含了节点的三阶邻域关系,更高阶的邻接矩阵能够保留更高阶的邻域关系。从实验结果看,不同数据集上最优的r值不同,但是在r值较大时模型的实验表现均受到限制,这是因为较高的r值使得节点邻域差异性减弱,每个节点聚合了过多远距离节点的特征信息,对低阶邻域的局部特征信息保留有限,降低了实验性能。
|
| 图 8 参数r实验结果 Fig. 8 Experimental results of parameter r |
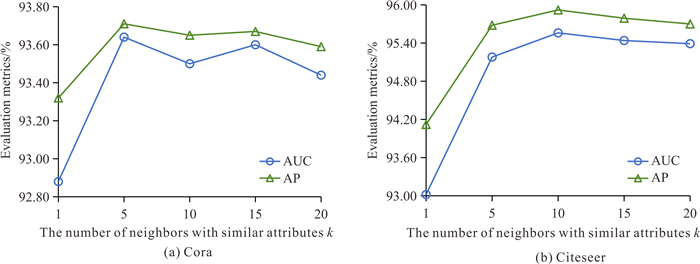
为了验证属性相似邻居数k对Self-VGAE性能的影响,使用不同的k值进行实验(图 9)。属性相似邻居数k与节点在属性空间的相似性有关,例如k值为3表示在属性空间为每个节点选择3个最接近的节点作为属性自监督信息。从实验结果看,两个数据集总体上均呈现先上升再下降的趋势,过高和过低的k值均未取得最佳的实验结果,这是因为k值过低无法保留充足的属性相似度信息,而k值过高导致大量属性相似度较低的噪声节点作为自监督信息,降低了实验性能。
|
| 图 9 参数k实验结果 Fig. 9 Experimental results of parameter k |
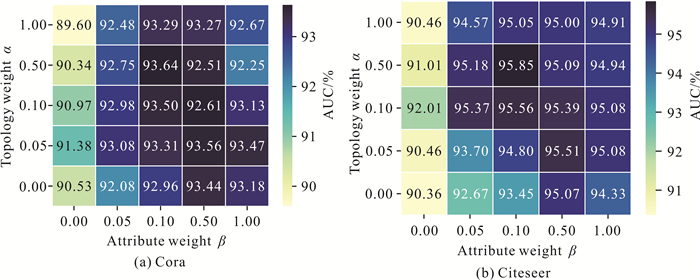
为了验证自监督约束权重系数α和β对Self-VGAE性能的影响,使用不同的α和β值进行实验(图 10)。权重系数α和β用于调整自监督信息在模型训练过程中的重要程度,使节点表示关注拓扑和属性信息的保留。从实验结果看,当一个系数固定时,另一个系数的实验表现随数值的增大呈现先上升再下降的趋势,这是因为过低的系数无法有效利用拓扑或属性自监督信息,而过高的系数使模型仅侧重于保留拓扑或属性自监督信息,降低了模型对原始图信息的表征能力。实验结果表明,当α=0或β=0(仅使用拓扑或属性作为自监督信息)、α和β均取较大值时,模型的实验表现均不佳,因此在优化过程中需要设置合适的权重系数α和β,平衡损失函数中拓扑与属性对比约束的比重。
|
| 图 10 参数α和β实验结果 Fig. 10 Experimental results of parameter α and β |
3.10 训练时间
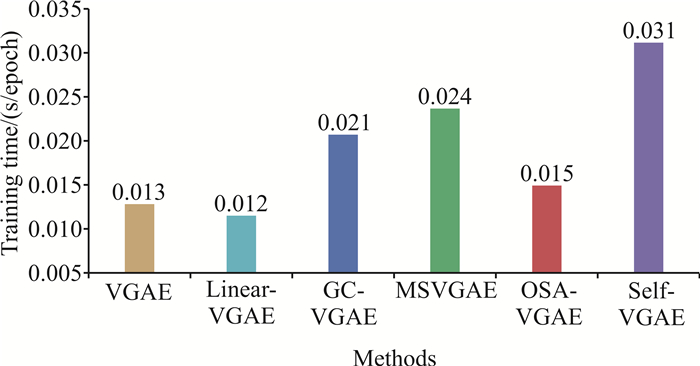
为了比较不同模型的训练复杂度,Cora数据集上迭代100次后单次迭代的平均训练时间(包括前向传播、损失函数计算、反向传播过程)如图 11所示。以原始的VGAE模型训练时间为基准,Linear-VGAE采用线性编码器进行特征提取,加快了模型训练速度;引入跨层连接的OSA-VGAE增加了层间特征融合步骤,使得训练速度略微增加;计算属性损失的GC-VGAE和计算多尺度信息的MSVGAE平均训练时间明显高于VGAE。本文提出的Self-VGAE虽然采用与VGAE相同的网络结构,但是为了充分保留原始图相关信息,额外借助属性和拓扑自监督约束对节点表示生成过程进行优化,导致模型的训练时间增加。
|
| 图 11 模型训练时间 Fig. 11 Model training time |
4 结论
本文提出一种基于自监督信息的图表示学习模型Self-VGAE,通过同时关注拓扑结构和节点属性的自监督约束增强了Self-VGAE对原始图信息的表征能力。实验结果表明,Self-VGAE生成的节点表示具有较强的通用性和泛化性,能够有效提升模型在3个基准数据集上的多个图分析任务的实验表现,并优于当前较为先进的基线模型。此外,相较以往依赖具体任务进行特征保留的图表示学习模型,Self-VGAE能够同时增强模型对节点相似性和差异性的保留能力、对拓扑结构的保持和推断能力以及高阶社区结构的表征能力。Self-VGAE仅通过改进模型优化方式提升实验性能,未考虑使用不同的编码器增强模型对原始数据特征的提取能力。因此,在后续工作中将引入多种改进方式,同时提升模型对原始图信息的提取和保留能力,并将其应用于社交网络安全问题检测和犯罪团伙挖掘等实际任务。
| [1] |
GHAREHCHOPOGH F S. An improved Harris hawks optimization algorithm with multi-strategy for community detection in social network[J]. Journal of Bionic Engineering, 2023, 20(3): 1175-1197. DOI:10.1007/s42235-022-00303-z |
| [2] |
DIVIÁK T. Structural resilience and recovery of a criminal network after disruption: a simulation study[J/OL]. Journal of Experimental Criminology, 2023 (2023-03-24)[2023-11-11]. https://doi.org/10.1007/s11292-023-09563-z.
|
| [3] |
PENG C Y, XIA F, NASERIPARSA M, et al. Knowledge graphs: opportunities and challenges[J]. Artificial Intelligence Review, 2023, 56: 13071-13102. DOI:10.1007/s10462-023-10465-9 |
| [4] |
XU M J. Understanding graph embedding methods and their applicationsm[J]. SIAM Review, 2021, 63(4): 825-853. DOI:10.1137/20M1386062 |
| [5] |
邹然, 柳杨, 李聪, 等. 图表示学习综述[J]. 北京师范大学学报(自然科学版), 2023, 59(5): 716-724. |
| [6] |
徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5): 755-780. |
| [7] |
CONG S, ZHOU Y. A review of convolutional neural network architectures and their optimizations[J]. Artificial Intelligence Review, 2023, 56(3): 1905-1969. DOI:10.1007/s10462-022-10213-5 |
| [8] |
袁立宁, 刘钊. 基于One-Shot聚合自编码器的图表示学习[J]. 计算机应用, 2023, 43(1): 8-14. |
| [9] |
HE M Y, ZHAO Q Q, ZHANG H. Multi-sample dual-decoder graph autoencoder[J]. Methods, 2023, 211: 31-41. DOI:10.1016/j.ymeth.2023.02.002 |
| [10] |
HY T S, KONDOR R. Multiresolution equivariant graph variational autoencoder[J]. Machine Learning: Science and Technology, 2023, 4(1): 015031. DOI:10.1088/2632-2153/acc0d8 |
| [11] |
WANG Y F, XU B Y, KWAK M, et al. A noise injection strategy for graph autoencoder training[J]. Neural Computing and Applications, 2021, 33: 4807-4814. DOI:10.1007/s00521-020-05283-x |
| [12] |
HUANG T J, PEI Y L, MENKOVSKI V, et al. On generalization of graph autoencoders with adversarial training[C]//Joint European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases. Cham: Springer, 2021: 367-382.
|
| [13] |
KIPF T N, WELLING M. Variational graph auto-encoders[EB/OL]. (2016-11-21)[2023-11-11]. http://arxiv.org/abs/1611.07308.
|
| [14] |
翟正利, 梁振明, 周炜, 等. 变分自编码器模型综述[J]. 计算机工程与应用, 2019, 55(3): 1-9. |
| [15] |
SALHA G, HENNEQUIN R, VAZIRGIANNIS M. Simple and effective graph autoencoders with one-hop linear models[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Cham: Springer, 2021: 319-334.
|
| [16] |
WU F, SOUZA A, ZHANG T Y, et al. Simplifying graph convolutional networks[C]//Proceedings of the 36th International Conference on Machine Learning. Cambridge: PMLR, 2019: 6861-6871.
|
| [17] |
KESER R K, NALLBANI I, ÇALIK N, et al. Graph embedding for link prediction using residual variational graph autoencoders[C]//Proceedings of the 28th Signal Processing and Communications Applications Conference. Piscataway: IEEE, 2020: 1-4.
|
| [18] |
RANI V, NABI S T, KUMAR M, et al. Self-supervised learning: a succinct review[J]. Archives of Computational Methods in Engineering: State of the Art Reviews, 2023, 30(4): 2761-2775. DOI:10.1007/s11831-023-09884-2 |
| [19] |
WANG J, LIANG J, YAO K, et al. Graph convolutional autoencoders with co-learning of graph structure and node attributes[J]. Pattern Recognition, 2022, 121: 108215. DOI:10.1016/j.patcog.2021.108215 |
| [20] |
FETTAL C, LABIOD L, NADIF M. Efficient graph convolution for joint node representation learning and clustering[C]//Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining. New York: ACM, 2022: 289-297.
|
| [21] |
LI D J, LI D, LIAN G. Variational graph autoencoder with adversarial mutual information learning for network representation learning[J]. ACM Transactions on Knowledge Discovery from Data, 17(3)45. |
| [22] |
XIE Y C, XU Z, ZHANG J T, et al. Self-supervised learning of graph neural networks: a unified review[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(2): 2412-2429. DOI:10.1109/TPAMI.2022.3170559 |
| [23] |
KUMAR P, RAWAT P, CHAUHAN S. Contrastive self-supervised learning: review, progress, challenges and future research directions[J]. International Journal of Multimedia Information Retrieval, 2022, 11(4): 461-488. DOI:10.1007/s13735-022-00245-6 |
| [24] |
HU Y, YOU H, WANG Z, et al. Graph-MLP: node classification without message passing in graph[EB/OL]. (2021-06-08)[2023-11-11]. http://arxiv.org/abs/2106.04051.
|
| [25] |
袁立宁, 李欣, 王晓冬, 等. 图嵌入模型综述[J]. 计算机科学与探索, 2022, 16(1): 59-87. |
| [26] |
GUO L, DAI Q. Graph clustering via variational graph embedding[J]. Pattern Recognition, 2022, 122: 108334. DOI:10.1016/j.patcog.2021.108334 |



