2. 北方民族大学图形图像国家民委重点实验室, 宁夏银川 750021
2. Laboratory of Graphics and Images of the State Ethnic Affairs Commission, North Minzu University, Yinchuan, Ningxia, 750021, China
近年来,随着风力发电需求的不断增长,准确预测风力发电功率变得越来越重要。风能的间歇性和随机性特点,使得风力发电功率的预测面临很大挑战,且已经引起风力发电企业的高度关注[1]。准确的风力发电功率预测对风力发电企业制定合理的发电交易计划以获得更多盈利,以及与电网调度部门制定运行计划、调整调度计划等方面都具有重要意义[2]。
目前,风电功率的短期预测方法主要分为统计模型、机器学习模型以及组合模型[3],统计模型和机器学习模型是常用的风电功率短期预测模型。统计模型包括自回归模型、滑动平均模型、自回归滑动平均模型、自回归差分滑动平均模型等[4]。机器学习模型包括支持向量机、随机森林、贝叶斯加性回归树、极限学习机等[5]。王永生等[6]在时间序列数据中加入时间窗口和金融因子,再将该数据输入极端梯度提升(XGBOOST)模型进行预测输出,结果显示,XGBOOST模型虽然具有较快的收敛速度,但是在面对波动较强的历史数据时预测效果不佳。Gu等[7]使用模糊C均值对风力特征进行聚类,并利用鲸鱼优化算法提高模型的收敛精度。但是这些方法在处理多元时间序列数据时存在局限性,在面对高维度、时空相关性、动态性和非线性等特征数据时,传统的统计模型和机器学习模型难以捕捉这些数据的内在特征和适应动态变化的环境,模型预测准确率不高。
近年来基于深度学习的模型被广泛应用于风力发电功率预测中。深度学习方法主要包括反向传播网络、循环神经网络(Recurrent Neural Network,RNN)、卷积神经网络(Convolutional Neural Networks,CNN)等。陈峰等[8]提出基于经验模态分解的特征构建方法,利用绳索算法进行特征选择,输入基于贝叶斯优化的长短期记忆神经网络的预测模型进行风电功率预测,但是该模型在面对波动较强的历史数据时预测效果不佳。吴坚等[9]介绍了一种基于奇异谱分析、CNN、门控循环单元(Gated Recurrent Unit,GRU)和支持向量回归(Support Vector Regression,SVR)的组合预测模型,基于奇异谱分析的预测模型能够获取时间序列中的时序演变特征和波动趋势,有效提升了不同步长下的预测精度。Huai等[10]利用CNN对原始输入数据进行特征提取和降维,GRU负责对处理后的时间序列进行预测,结果表明,所提出的CNN_GRU模型在预测表现中具有最佳效果。Liu等[11]利用奇异谱分析将原始风速序列分解为一个主要趋势分量和一些细节分量,随后采用CNN-GRU网络预测趋势分量,最后采用SVR对细节分量进行预测,实验结果表明, 所提出的模型在预测性能上获得了良好的结果。以上方法均需要大量的计算资源和训练数据,对复杂数据的处理能力有限,且对不同环境的风电数据存在泛化能力不足的问题。
组合模型是一种将多个子模型进行组合或者将各个子模型的结果加权输出的方法。其中,最小二乘支持向量机和径向基函数神经网络加权组合的预测方法是一种常用方法[12]。该方法通过训练多个子模型,如支持向量机(Support Vector Machine,SVM)、长短期记忆网络(Long Short-Term Memory,LSTM)、差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)等,对原始数据进行预测,然后将每个子模型的预测结果进行加权平均,得到最终的预测结果。由于不同的子模型在处理不同类型的数据时可能存在效果不统一、难以平均优化的问题[13],因此,在实际应用中需要根据具体情况人工选择合适的子模型,并进行大量的加权调整和优化,才能提高预测精度和稳定性。
针对以上问题和不足,本研究提出一种新颖的风电功率预测模型VMD-GRAU,该模型融合了变分模态分解(Variational Mode Decomposition, VMD)、门控循环注意力(Gated Recurrent Attention Unit,GRAU)模型,设计注意门来增强GRU对重要序列特征的捕捉能力和稳健性, 设计误差修正模块来降低风电功率预测的随机性和波动性影响,在损失函数中添加稀疏正则化项来防止模型过拟合,最后在真实数据集上验证算法的准确性与有效性。
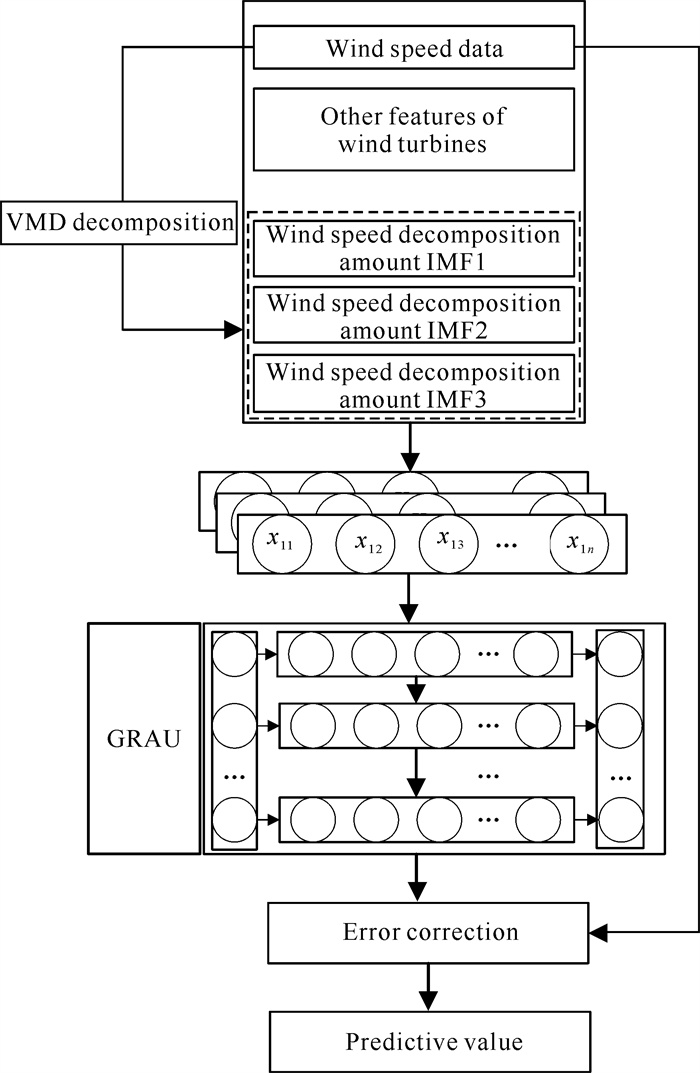
1 方法与理论 1.1 VMD-GRAU模型本研究提出了一种基于信号分解和深度学习的风电功率预测模型VMD-GRAU,如图 1所示。通过使用VMD对信号进行分解,提取不同时间尺度的特征,避免了模态混合和假峰值问题。同时提出GRAU模型,设计了注意门来增强GRU长期记忆的能力,并帮助记忆单元快速丢弃不重要的内容,记住对时序预测重要的部分,从而增强模型对数据特征的捕捉能力和稳健性;设计误差修正模块来降低风电预测的随机性和波动性影响,最后在传统的损失函数中添加稀疏正则化项来防止模型过拟合并增强模型的泛化性。
|
| 图 1 VMD-GRAU预测模型的预测结构 Fig. 1 Prediction structure of VMD-GRAU prediction model |
1.2 变分模态分解
VMD是一种信号分解技术,它可以将原始信号分解成若干个本征模态函数(Intrinsic Mode Functions, IMF)[14],这些IMF可以用于分析信号的频率特征和时域特征。VMD也是一种降噪算法,可用于从高维数据集中分离出低维信号,这些信号代表了数据集的多个模态特征。因此,VMD是一种自适应的分解方法,可以自动适应信号的局部特性。在风力发电机功率预测中,VMD可以有效地分离出风力发电机功率数据集的多个模态,这些模态代表了影响风力发电机功率的因素,如风速、天气条件、风力涡轮机的状态等。此外,VMD可以避免模态混合和假峰值等问题,比传统的降噪算法(如主成分分析法和独立成分分析法)更有效。对于给定的信号x(t),将其分解为K个本征模态函数的叠加。
| $ x(t)=\sum\nolimits_{k=1}^K u_k(t)+r_k(t), $ | (1) |
式中,uk(t) 为第k个本征模态函数在t时刻的值,rk(t) 为余项,t为时间步。
本征模态函数满足在时域上是单调振荡的,其Hilbert变换的辐角是常数。本质上,本征模态函数是信号的局部振动模式。通过将信号分解成多个本征模态函数可以对信号的不同特征进行分析。
VMD分解通过解决如下的凸优化问题来计算本征模态函数和余项。
| $ \begin{aligned} & \mathrm {min}_{u_k, f_k} \frac{1}{2} \sum\nolimits_{i=1}^N \sum\nolimits_{k=1}^K\left[u_k(t)-f_k(t)\right]^2+ \lambda \sum\nolimits_{k=1}^K\left|\sum\nolimits_{i=1}^N \gamma_k(t) u_k(t)\right|, \end{aligned} $ | (2) |
式中,fk(t) 为第k个本征模态函数的重构信号,γk(t)为权重系数,λ为正则化参数,N为信号长度。
为了求解上述问题需要使用迭代方法。首先,随机初始化本征模态函数uk(t)和权重系数γk(t),然后通过交替最小化2个步骤来进行更新。
① 给定权重系数γk(t),通过最小化下列二次代价函数来更新本征模态函数。
| $ \begin{aligned} & \mathrm {min}_{u_k} \frac{1}{2} \sum\nolimits_{i=1}^N\left[u_k(t)-f_k(t)\right]^2+ \lambda\left|\sum\nolimits_{i=1}^N \gamma_k(t) u_k(t)\right|。\end{aligned} $ | (3) |
通过Proximal operator方法求解。首先计算一个N信号长度的矩阵Pk。
| $ \boldsymbol{P}_k(i, j)=\frac{1}{2} \exp \left(-\frac{(i-j)^2}{2 \sigma_k^2}\right), $ | (4) |
式中,i和j分别代表时间序列中两个不同时刻的索引用于计算协方差矩阵,σk是与第k个本征模态函数相关的宽度参数。更新本征模态函数表示如下:
| $ u_k=\frac{\sum\nolimits_{i=1}^N \boldsymbol{P}_k(i, j) f_k(i)}{\sum\nolimits_{i=1}^N \boldsymbol{P}_k(i, j) \gamma_k(i)}, $ | (5) |
式中,fk(i)表示第i个本征模态函数的重构信号,γk(i)表示权重系数。
② 给定本征模态函数uk(t),通过最小化下列二次代价函数J(w)来更新权重系数。
| $ \begin{gathered} J(w)=\frac{1}{2} \sum\nolimits_{k=1}^K\left[u_k(t)-\sum\nolimits_{j=1}^M w_{k j} y_j(t)\right]^2+ \frac{v}{o} \sum\nolimits_{i=1}^M\left[y_j(t)-y_j(t-1)\right]^2, \end{gathered} $ | (6) |
式中,K为本征模态数量(设置为3),M是权重系数的数量,wkj为第k个本征模态函数与第j个输入信号之间的权重系数,yj(t)代表模型在时间t对第j个输入信号进行的预测值,v为平滑系数,yj(t-1)代表模型在时间t-1对第j个输入信号进行的预测值。目标是最小化代价函数J(w),其中第一项表示拟合误差,表示本征模态函数与输入信号之间的差异,第二项表示平滑性约束,表示输入信号的变化应该尽可能平滑。通过最小化代价函数,可以得到最优的权重系数w,从而实现对输入信号的重构和预测。
1.3 GRU模型GRU是RNN的变种。与传统的RNN相比,GRU引入了门控机制,可以更好地捕捉时间序列数据中的长期依赖关系,避免了梯度消失和梯度爆炸的问题。
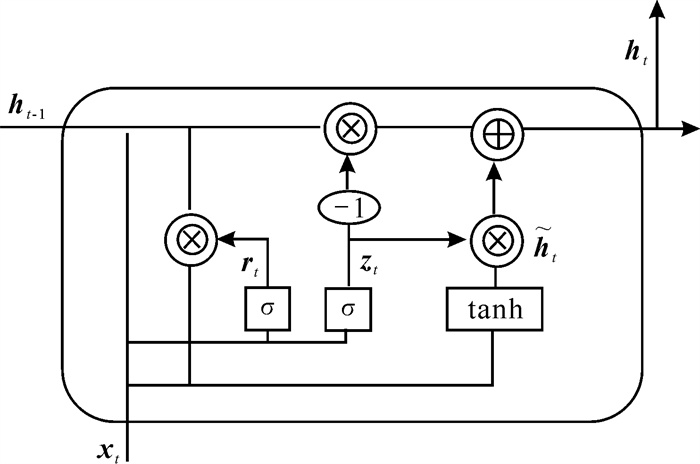
如图 2所示,一个典型的GRU的结构可以分为更新门
|
| 图 2 GRU模型 Fig. 2 GRU model |
首先,对于一个输入序列xt,一个上一时间步的隐藏状态ht-1以及GRU单元的权重矩阵W和偏置向量b计算更新门。
| $ \boldsymbol{z}_t=\sigma\left(\boldsymbol{W}_z \boldsymbol{x}_t+\boldsymbol{U}_z \boldsymbol{h}_{t-1}+\boldsymbol{b}_z\right) \text { 。} $ | (7) |
计算重置门:
| $ \boldsymbol{r}_t=\sigma\left(\boldsymbol{W}_r \boldsymbol{x}_t+\boldsymbol{U}_r \boldsymbol{h}_{t-1}+\boldsymbol{b}_r\right), $ | (8) |
式(7)和式(8)中σ为sigmoid函数,U为权重矩阵。
计算候选隐藏状态
| $ \widetilde{\boldsymbol{h}}_t=\tanh \left(\boldsymbol{W} \boldsymbol{x}_t+\boldsymbol{U}\left(\boldsymbol{r}_t \times \boldsymbol{h}_{t-1}\right)+\boldsymbol{b}\right) 。$ | (9) |
最后,GRU通过更新门来计算当前隐藏状态ht。
| $ \boldsymbol{h}_t=\left(1-\boldsymbol{z}_t\right) \times \boldsymbol{h}_{t-1}+\boldsymbol{z}_t \times \widetilde{\boldsymbol{h}}_t $ | (10) |
通过对输入数据进行门控操作,GRU可以有效地捕捉时间序列数据中的长期依赖关系,提高序列数据的建模能力。
1.4 GRAU模型在风电功率预测中,由于风速环境是不断变化的,捕捉风速环境的动态变化对于风电功率预测至关重要,传统GRU时间序列预测模型在捕获序列之间的依赖方面有所欠缺。注意力(Attention)机制是一种可以根据输入数据的不同部分自适应地赋予不同的权重,从而使模型更加关注对预测结果有贡献的输入部分的机制。注意力机制可以赋予每个时间步的GRU输出不同的权重,权重取决于当前的风速环境和历史的风速环境,模型的预测结果可以更好地反映当前的风速环境,从而提高动态变化的预测效果。本研究将注意力机制思想无缝集成到GRU算法内部,提出GRAU模型。设计注意门来增强GRU长期记忆的能力,并帮助记忆单元快速丢弃不重要的内容,记住对时序预测重要的部分。GRAU模型能够通过自适应地选择区域或位置序列,从序列数据中提取信息,并在学习过程中更加关注所选区域。
在GRAU模型中,注意力接收序列信息x1, x2, …, xt和最后时刻的隐藏状态ht-1,以学习可以表达这些信息重要性的权重矩阵 At,表示如下:
| $ \begin{aligned} & \quad \boldsymbol{a}_t=f_M\left(\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right) \boldsymbol{A}_t=\frac{\exp \left(\boldsymbol{a}_t\right)}{\sum\nolimits_{t=1}^{\mathrm{T}} \exp \left(\boldsymbol{a}_t\right)} \hat{\boldsymbol{h}}_t= \tanh \left(\boldsymbol{A}_t\left[\boldsymbol{x}_t, \boldsymbol{h}_{t-1}\right]\right), \end{aligned} $ | (11) |
式中,at为概率向量;fM为注意力学习函数,是仅由ht-1和xt决定的学习函数,使用速度快的前馈神经网络实现。采用多头注意力机制,输入向量的维度变为原来的1/M, 输入到M个前馈神经网络,所有输出向量取平均值得到at。每个注意力头都可以学习不同的注意力模式,因此多头注意力机制可以捕捉到输入序列中不同部分之间的复杂关系,从而提高模型的表示能力,经实验最后确定本研究的注意力头个数为4,在模型速度和准确率之间达到平衡。最后归一化后得到的At,表示第t时间步对模型预测的重要性。
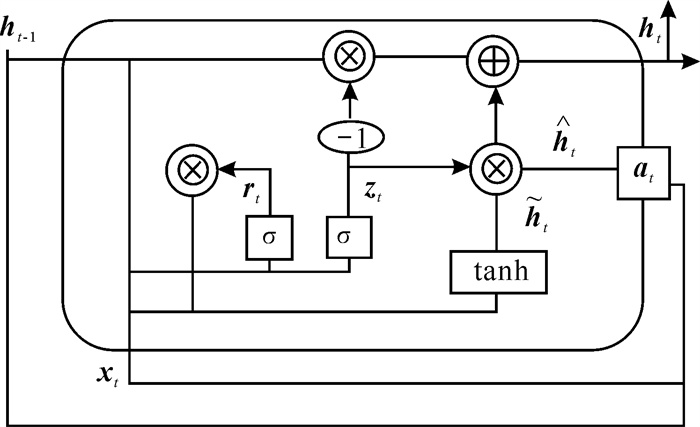
图 3是一个完整的GRAU结构,其中隐藏状态ht-1和输入xt中的向量被送到学习函数fM中产生一个概率向量at,可以理解为学习到的历史经验和此刻的风电状态进行融合得到向量
| $ \boldsymbol{h}_t=\left(1-\boldsymbol{z}_t\right) \boldsymbol{h}_{t-1}+\boldsymbol{z}_t \tilde{\boldsymbol{h}}_t+\boldsymbol{z}_t \widehat{\boldsymbol{h}}_t / \varepsilon, $ | (12) |
式中,ε为注意力门的占比,实验中经过超参数寻优后一般设置为2。
|
| 图 3 GRAU模型 Fig. 3 GRAU model |
1.5 误差修正模块
误差是指预测值与观测值之间的偏差。观测实验中的预测差,可以得知在某些时期的预测误差较大。由于前期的预测模型是基于历史风电特征数据,其预测虽然可以有效地反映风电的趋势但是无法获得风电的随机和波动因素。因此,本研究提出一种修正误差的方法来提高预测精度。首先,定义预测模型的预测误差en为
| $ e_n=P_n-\hat{P}_n, $ | (13) |
式中,Pn和
| $ \rho_{X, Y}=\frac{E\left[\left(X-\mu_X\right)\left(Y-\mu_Y\right)\right]}{\zeta_X \zeta_Y}, $ | (14) |
式中,ρX, Y是X和Y的相关系数,E为计算平均值,μ和ζ分别代表变量的平均值和均方差。如果两个变量X和Y相关,则ρX, Y的值接近1,在不同环境的数据集下计算得到模型预测误差与风速特征的相关系数最高,这与直觉相符,说明可以利用风速特征对预测误差进行优化调整。
本研究使用简单的两个全连接层实现误差修正模块,具有参数量少、计算速度快的优点。具体实现:第一个全连接层的输出神经元数量为10,激活函数选择ReLU。神经元数量通过超参数寻优确定。这一层的作用是对模型的输出进行进一步的非线性变换。第二个全连接层的输出神经元数量为1,没有设置激活函数。这一层的作用是将前一层的输出映射到单个数值,作为最终的修正输出。这两个全连接层的参数会在训练过程中自动学习,以便最小化模型预测结果与真实结果之间的误差。在训练期间,优化器会根据损失函数(均方误差)的梯度调整全连接层的权重和偏置,以逐步改进模型的性能。最终,通过将修正模型的输出与原始模型的输出相加,从而获得更精确的预测结果。
1.6 使用稀疏正则化的损失函数在模型训练过程中,如果只尝试拟合输入的训练数据,将极大概率导致模型过拟合并降低模型的泛化性。林东方等[15]指出均方误差(Mean Squared Error,MSE)作为损失函数会降低模型的泛化性能,稀疏正则化有助于模型泛化性的提升。本研究为避免过拟合,在训练阶段改进了损失函数Loss,添加正则化项和稀疏项。
| $ \text { Loss }=\frac{1}{m} \sum\nolimits_{i=1}^m\left(P_i-\widehat{P}_i\right)^2+\alpha \times \mathit{Ω}_w+\beta \times \mathit{Ω}_S, $ | (15) |
式中,Pi表示风力发电功率的实际观测值,
| $ \mathit{Ω}_w=\frac{1}{2} \sum\nolimits_l^L \sum\nolimits_i^m \sum\nolimits_j^n\left(W_{i j}^l\right)^2, $ | (16) |
式中,L和m分别表示隐藏层和样本总数,n表示样本数据使用的变量数目,
| $ \begin{aligned} & \mathit{Ω}_S=\sum\nolimits_{i=1}^s K L_D\left(\frac{p}{p_i}\right)=\sum\nolimits _{i=1}^s p \log \left(\frac{p}{p_i}\right)+(1-p) \log \left(\frac{1-p}{1-p_i}\right) \end{aligned} $ | (17) |
式中,p是神经元的期望激活值,pi是神经元i的平均激活值,KLD表示Kullback-Leibler (KL)散度。当神经元的实际激活值和期望激活值相同时,稀疏正则化项将为0。随着期望激活值和平均激活值之间差异的增加,ΩS项将增加。损失函数中的L2权重正则化项和稀疏正则化项有助于提升GRAU模型的泛化性能。
2 结果与分析实验在Linux操作系统下的Pycharm平台进行,CPU为Intel(R) Xeon(R) Gold 6154,内存128 G,GPU为NVIDIA TITAN V,显存24 G。
为验证所提方法的有效性,采用龙源电力集团股份有限公司独有的空间动态风力发电预测数据集。数据采样周期为10 min,共记录了245 d的风电功率数据,数据集记录了风机的风速、风向等9个特征和风电功率。
本研究提出的VMD-GRAU模型超参数如表 1所示。
| 超参数 Hyperparameters |
数值 Value |
| GRU hidden layers | 64 |
| Total number of attention heads | 4 |
| Attention head dimension | 64 |
| Regularization term coefficient | 0.2 |
| Sparse term coefficient | 0.2 |
| Activation function | ReLU |
| Learning rate | 0.001 |
2.1 模型评价指标
首先将数据集的80%作为训练集,20%作为测试集,训练集的数据用作模型的训练输入,测试集检测模型的预测效果。为了检测模型的预测效果,选择平均绝对误差(MAE)、均方根误差(RMSE)和拟合优度(R2)来评价预测结果,其表达式分别为
| $ \mathrm{MAE}=\frac{1}{n} \sum\nolimits_{i=1}^n\left|\hat{y}_i-y_i\right|, $ | (18) |
| $ \text { RMSE }=\sqrt{\frac{1}{n} \sum\nolimits_{i=1}^n\left(\hat{y}_i-y_i\right)^2}\;\;\;\;, $ | (19) |
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2}{\sum\limits_{i=1}^n\left(y_i-\bar{y}_i\right)^2}, $ | (20) |
式中,n为预测样本数,yi和
VMD分解风速信号时,需要事先确定分解模态数K,每个分量模态根据中心频率的不同来区分。在进行VMD分解时,VMD分解的分解个数对模型预测至关重要[16]。
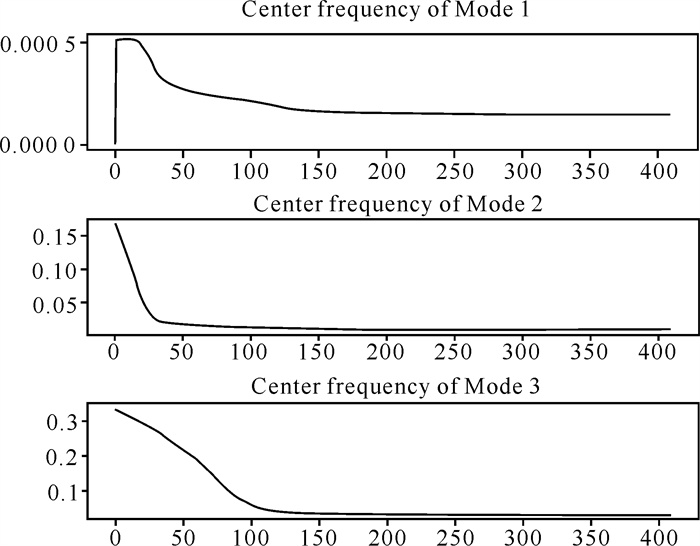
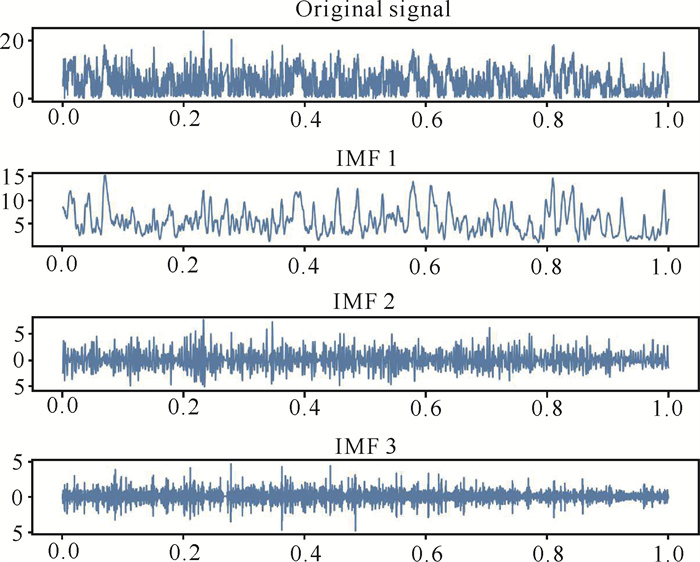
经过多次对比试验,将K设置为3时,各个模态的差异较大,且模态3模态中心频率值在0.05-0.35波动,保留的特征更多(图 4)。因此,本研究对历史风速进行VMD分解时的模态数设置为3。原始风速数据和经VMD分解后的结果如图 5所示。其中IMF1-IMF3为分解出的从低频到高频的风速分量。
|
| 图 4 K=3时各模态中心频率图 Fig. 4 Center frequency diagram of each mode when K=3 |
|
| 图 5 VMD分解结果 Fig. 5 VMD decomposition results |
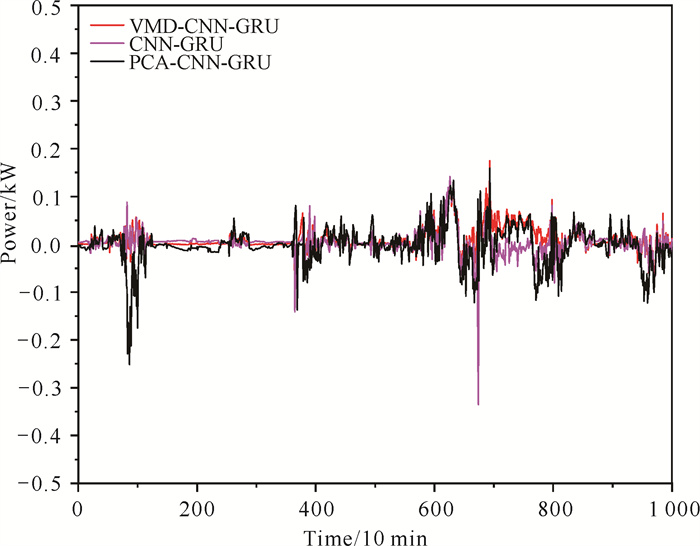
为了说明添加VMD分解后的特征序列相比原始风速特征序列对风电功率预测模型有提升效果,对两种情况做了仿真分析。其中,基础预测模型选择CNN-GRU预测算法, VMD-CNN-GRU为添加了VMD分解特征的算法。模型预测误差的输出结果如图 6所示,可以看出,经VMD分解后的风速分量作为训练输入比原始风速更能反映风电功率的变化。与传统的使用基于PCA的PCA-CNN-GRU方法相比,经VMD分解后风速分量的预测误差几乎都在[-50, 200],而PCA-CNN-GRU的预测误差几乎都在[-190, 210]。
|
| 图 6 各模型预测结果对此 Fig. 6 Prediction results of each model |
原始风速预测功率的误差绝对值在200 kW以上的很多,有的预测点误差超过300 kW。证明添加VMD方法的有效性。
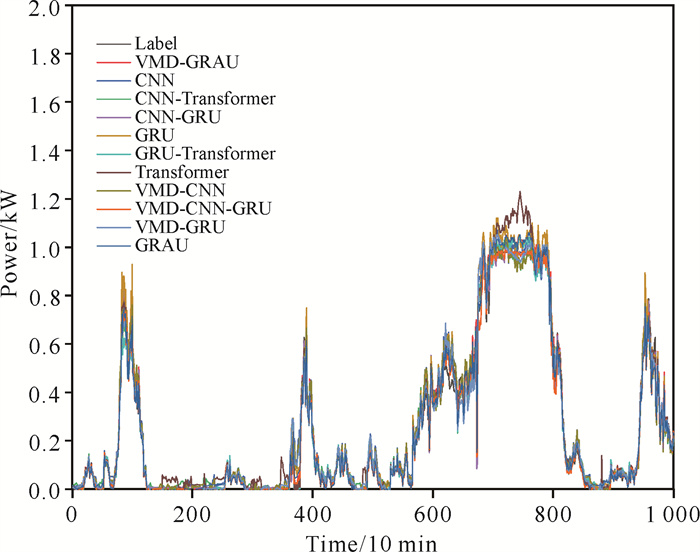
为了充分测试本研究提出的VMD-GRAU模型的预测能力,添加4组常用单一预测模型与3组组合预测模型进行对比。其中:单一预测模型分别为GRU[17]、CNN、CNN-GRU[18]、CNN-Transformer;组合预测模型分别为VMD-CNN[19]、VMD-CNN-GRU[20]、VMD-GRU[21]。选取1 000 min的风电数据进行预测,对比结果如图 7所示。
|
| 图 7 各模型预测结果对比 Fig. 7 Comparison on prediction results of different models |
从图 7的预测结果的对比中可以看出,本研究提出的VMD-GRAU模型的预测精度要高于其他模型。对于风速功率剧烈抖动或者波动较大的地方,本研究提出的模型相比其他模型依然具有较好的拟合效果,这说明了本研究提出的模型能够有效提取风速序列的细节信息,取得更高的预测精度,且误差模块能够较好地抵御风电的随机和波动因素。不同预测模型在完整的测试集上的各个评价结果如表 2所示。
| 预测模型 Prediction model |
MAE | RMSE | R2 |
| VMD-GRAU | 0.022 | 0.016 | 0.995 |
| GRAU | 0.025 | 0.022 | 0.990 |
| CNN | 0.028 | 0.042 | 0.978 |
| CNN-Transformer | 0.024 | 0.034 | 0.989 |
| CNN-GRU | 0.028 | 0.016 | 0.988 |
| GRU | 0.030 | 0.044 | 0.981 |
| GRU-Transformer | 0.025 | 0.040 | 0.985 |
| Transformer | 0.032 | 0.049 | 0.977 |
| VMD-CNN | 0.028 | 0.041 | 0.984 |
| VMD-CNN-GRU | 0.023 | 0.030 | 0.991 |
| VMD-GRU | 0.025 | 0.041 | 0.984 |
由表 2可以看到本研究提出的VMD-GARU模型取得了最好的预测效果,预测的MAE相较于GRU模型提升了26%,相较于Transformer模型提升了31%。由此可以得出,在风电功率预测上,本研究提出的VMD-GARU模型预测精度最高,预测效果最好。
使用训练好的模型在不同地区、不同风机上的数据集进行泛化性测试,选择R2作为评价指标,每个地区选择3个风机测试,平均运行5次,不同方法的平均预测结果如表 3所示。
| 预测模型 Prediction model |
R2 | ||
| 地区2风机(1-3) Region 2(wind turbine 1-3) |
地区3风机(4-6) Region 3(wind turbine 4-6) |
地区4风机(7-9) Region 4(wind turbine 7-9) |
|
| GRU | 0.698 | 0.801 | 0.754 |
| CNN-GRU | 0.674 | 0.644 | 0.521 |
| AGRU | 0.741 | 0.602 | 0.688 |
| VMD-GRU | 0.799 | 0.911 | 0.784 |
| Transformer | 0.687 | 0.904 | 0.860 |
| VMD Transformer | 0.707 | 0.907 | 0.884 |
| VMD-GRAU | 0.907 | 0.921 | 0.938 |
从表 3可以明显看出,本研究提出的VMD-GRAU模型在不同环境下依然具有较好的泛化性,相比基线模型GRU提高了15%-30%。而其他模型(如Transformer、VMD Transformer、VMD-GRU)虽然在某些地区能够取得较好的测试性能,但是并不具备在所有地区均稳定的泛化性。
3 结论针对风电功率随机性较强,现有风电功率短期预测模型难以捕捉风电时序关联特征的问题,本研究首先采用变分模态分解得到影响风电预测的模态特征;然后提出GRAU模型,设计注意门来增强模型对数据特征的捕捉能力和稳健性,设计误差修正模块来降低风电预测的随机性和波动性影响;最后在传统的损失函数中添加稀疏正则化项来防止模型过拟合。实验结果表明,本研究提出的模型相比传统模型GRU和Transformer,其预测的MAE提升了26%-31%;在不同环境下依然具有较好的泛化性,相比基线模型GRU提高了15%-30%。
| [1] |
薛禹胜, 雷兴, 薛峰, 等. 关于风电不确定性对电力系统影响的评述[J]. 中国电机工程学报, 2014, 34(29): 5029-5040. |
| [2] |
FOLEY A M, LEAHY P G, MARVUGLIA A, et al. Current methods and advances in forecasting of wind power generation[J]. Renewable Energy, 2012, 37(1): 1-8. DOI:10.1016/j.renene.2011.05.033 |
| [3] |
WANG X C, GUO P, HUANG X B. A review of wind power forecasting models[J]. Energy Procedia, 2011, 12: 770-778. DOI:10.1016/j.egypro.2011.10.103 |
| [4] |
WANG Y, ZOU R M, LIU F, et al. A review of wind speed and wind power forecasting with deep neural networks[J]. Applied Energy, 2021, 304: 117766. DOI:10.1016/j.apenergy.2021.117766 |
| [5] |
HANIFI S, LIU X L, LIN Z, et al. A critical review of wind power forecasting methods: past, present and future[J]. Energies, 2020, 13(15): 3764. DOI:10.3390/en13153764 |
| [6] |
王永生, 关世杰, 刘利民, 等. 基于XGBoost扩展金融因子的风电功率预测方法[J]. 浙江大学学报(工学版), 2023, 57(5): 1038-1049. |
| [7] |
GU B, HU H, ZHAO J, et al. Short-term wind power forecasting and uncertainty analysis based on FCM-WOA-ELM-GMM[J]. Energy Reports, 2023, 9: 807-807. DOI:10.1016/j.egyr.2022.11.202 |
| [8] |
陈峰, 余轶, 徐敬友, 等. 基于Bayes-LSTM网络的风电出力预测方法[J]. 电力系统保护与控制, 2023, 51(6): 170-178. |
| [9] |
吴坚, 项颂, 阎诚, 等. 基于奇异谱分析的超短期风电功率多步预测[J]. 可再生能源, 2021, 39(11): 1548-1555. |
| [10] |
HUAI N N, DONG L, WANG L J, et al. Short-term wind speed prediction based on CNN_GRU model [C]//2019 Chinese Control and Decision Conference (CCDC). Nanchang, China: IEEE, 2019.
|
| [11] |
LIU H, MI X W, LI Y F, et al. Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, convolutional Gated Recurrent Unit network and Support Vector Regression[J]. Renewable Energy, 2019, 143: 842-854. DOI:10.1016/j.renene.2019.05.039 |
| [12] |
SHI J, DING Z H, LEE W J, et al. Hybrid forecasting model for very-short term wind power forecasting based on grey relational analysis and wind speed distribution features[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 521-526. DOI:10.1109/TSG.2013.2283269 |
| [13] |
SIDERATOS G, HATZIARGYRIOU N D. An advan-ced statistical method for wind power forecasting[J]. IEEE Transactions on Power Systems, 2007, 22(1): 258-265. DOI:10.1109/TPWRS.2006.889078 |
| [14] |
HUANG Y, DENG Y. A new crude oil price forecasting model based on variational mode decomposition[J]. Knowledge-Based Systems, 2021, 213: 106669. DOI:10.1016/j.knosys.2020.106669 |
| [15] |
林东方, 朱建军, 付海强, 等. 均方误差意义下的正则化参数二次优化方法[J]. 测绘学报, 2020, 49(4): 443-451. |
| [16] |
ZHANG Y G, ZHAO Y, KONG C H, et al. A new prediction method based on VMD-PRBF-ARMA-E model considering wind speed characteristic[J]. Energy Conversion and Management, 2020, 203: 112254. DOI:10.1016/j.enconman.2019.112254 |
| [17] |
XIAO Y L, ZOU C Z, CHI H T, et al. Boosted GRU model for short-term forecasting of wind power with feature-weighted principal component analysis[J]. Energy, 2023, 267: 126503. DOI:10.1016/j.energy.2022.126503 |
| [18] |
WANG Y K, SONG Z D, LIU Y C, et al. Wind power Prediction based on the fusion of CN N-GRU combined neural network and attention mechanism [C]//2022 IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). Beijing, China: IEEE, 2022: 698-702.
|
| [19] |
XIONG B R, MENG X Y, XIONG G, et al. Multi-bran-ch wind power prediction based on optimized variational mode decomposition[J]. Energy Reports, 2022, 8: 11181-11191. DOI:10.1016/j.egyr.2022.08.271 |
| [20] |
ZHAO Z N, YUN S N, JIA L Y, et al. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features[J]. Engineering Applications of Artificial Intelligence, 2023, 121(4610): 105982. |
| [21] |
HOSSAIN M A, GRAY E M, ISLAM M R, et al. Forecasting very short-term wind power generation using deep learning, optimization and data decomposition techniques [C]//202124th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju. Korea: IEEE, 2021: 323-327.
|



