2. 广西大学计算机与电子信息学院, 广西南宁 530004
2. School of Computer, Electronics and Information, Guangxi University, Nanning, Guangxi, 530004, China
随着无线通信的发展和无线设备数量的不断增加,增强移动宽带、超可靠与低时延通信、海量物联网通信成为5G移动通信时代的三大主要需求[1]。为了解决频谱紧缺、能源短缺等问题对网络性能提升的限制,涌现了诸如全双工(Full-Duplex,FD)、无线携能通信(Simultaneous Wireless Information and Power Transfer, SWIPT)、异构蜂窝网络(Heterogeneous Cellular Networks, HCN)等一大批5G关键技术[2-4]。传输速率、网络容量等通信性能的不断提升增加了无线通信网络的能耗,这增加了成本和碳排放量。能量效率(Energy Efficiency, EE)综合考虑了系统效益和能耗两个指标,同时满足绿色通信以及高通信质量的要求,成为衡量无线通信网络的关键性能指标。SWIPT系统通过对射频(Radio Frequency,RF)信号的双重利用,使得信息和能量信号同时传输。由于无线信道的广播特性,无线传输很容易被攻击或窃听,因此兼顾能量传输和信息安全一直是无线通信中需要重点关注的极具挑战性的问题[4-6]。由于传统基于计算复杂度的上层加密方法已无法有效抵抗新兴技术带来的安全风险,基于无线信道特性(如衰落、噪声和干扰等)的物理层安全技术成为增强安全性的有效手段[6]。
利用多天线带来的空间增益,基站可以发射高度定向的波束成形来增强合法信道的信干噪比,是一种提升通信安全的有效方法。Chen等[7]在下行链路(Downlink,DL)上同时进行SWIPT的FD安全传输,联合优化最优发射波束成形向量设计与功率分流(Power Splitting,PS)因子及上行链路(Uplink,UL)发射功率,在能量收集(Energy Harvesting, EH)和安全速率约束下最小化系统功率。Viet tuan等[8]考虑了窃听者下行信道状态信息(Channel State Information,CSI)不完美的情况,提出一种带有惩罚函数的迭代算法来获得近似的秩一矩阵。Ma等[9]基于公平性考虑,提出一种基于半定松弛和连续凸近似(Successive Convex Approximation,SCA)的集中波束成形设计算法。鲍慧等[10]针对FD认知网络中自能量回收(Self-Energy Recovery,SER)与安全通信之间的平衡,确定了系统安全能量效率(Secrecy Energy Efficiency,SEE)最大化问题,提出了一种基于泰勒级数展开和拉格朗日对偶分解法的迭代算法, 以得到PS因子和传输协方差矩阵的最优设计方案。Zheng等[11]研究在非线性能量收集模型下的多输入单输出全双工SWIPT系统,通过联合优化上行链路和下行链路波束成形矩阵来提高系统的鲁棒性。Xu等[12]提出一种多输入多输出FD多跳中继SWIPT移动边缘计算系统,该系统在满足延迟和能量约束的情况下能够最大限度地减少系统能耗。Liu等[13]提出一种在不完全CSI下的多输入多输出FD中继物联网系统,研究了在发射功率和收获能量约束下系统安全速率最大化的中继波束成形优化问题。Lu等[14]提出一种SWIPT的鲁棒波束成形设计方案,方案中的速率分割模式和基于PS的EH接收机分别用于安全信息传输和能量收集。
此外,增大窃听者处的信号噪声以降低其信干噪比的方法也可以保护合法通信安全,例如在通信过程中加入人工噪声(Artificial Noise,AN)以降低窃听者的通信质量。Li等[15]联合设计信息、AN波束成形矢量与合法用户的上行发射功率,并通过数值结果验证了联合设计方案的有效性以及FD在改进SEE方面的优势。Chen等[16]针对具有SWIPT的FD无线供电中继网络提出一种联合放大转发波束成形和AN协方差矩阵的资源分配策略,该方案优于无AN辅助的其他基线方案。Li等[17]研究信息信号与AN波束成形联合设计如何影响保密能效最大化和能量收集效率最大化这两个相互冲突的优化目标,并提出一种基于加权切比雪夫方法的多目标优化设计方案来揭示SEE和能量收集效率之间的平衡。雷维嘉等[18]研究并提出FD合法节点发射零空间AN的物理层安全方案。丁青锋等[19]提出一种基于天线选择的零空间AN辅助方案以最大化系统的安全容量。在多窃听场景下,杨广宇等[20]以优化最差保密能效为目标,提出一种基于Dinkelbach方法的两级优化迭代算法对波束成形矩阵、AN协方差矩阵和功率分配比进行联合设计。Li等[21]将AN应用于两层HCN下行安全SWIPT波束成形设计中,在宏观用户信干噪比要求、发射功率约束和能量收集约束下最大限度地提高保密率,并在此基础上进一步考虑CSI完美和不完美两种情况下信息接收端保密率的提高[22]。Zhang等[23]在考虑用户公平性的基础上,提出跨层多单元协调信号与AN波束形成设计方案,并开发一种基于交替方向乘子法的分布式解决方案最大化全局SEE。基于智能反射表面辅助技术,朱政宇等[24, 25]提出一种多输入多输出FD中继SWIPT物联网系统的安全波束成形设计方法,在非线性EH模型和中断率概率约束下通过联合优化IRS的发射波束成形和相移来最小化总发射功率。Fernandez等[26]研究FD功率信标和EH设备之间的保密性能和能效权衡问题,分析SWIPT策略中最佳分时因子的设计、不同波束形成策略对系统正常运行以及能量和信息传输信道相关性的影响。
综上所述,虽然研究人员对FD、SWIPT与HCN的集成和信息传输安全等问题进行研究,但是大部分研究仅考虑单一的集成方式,针对FD异构SWIPT网络场景能效、安全的研究较少,且部分研究的网络系统中仅基站是FD,而用户是半双工。因此本研究针对FD异构SWIPT网络中的能效优化和传输安全问题,从物理层安全角度出发,提出一种基于AN辅助的FD异构SWIPT网络安全波束成形设计方案,在满足安全发射功率阈值、最低安全速率以及收集能量等约束下,通过联合优化AN、信息信号波束成形矢量和上行发射功率,最大化SEE。
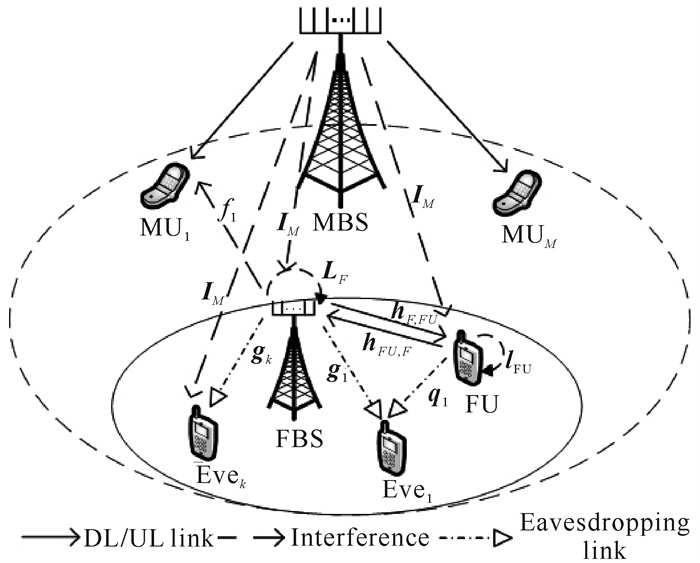
1 系统模型图 1是具有SWIPT的FD两层异构蜂窝网络,其中宏蜂窝包括1个宏基站(Macro Base Station,MBS)和M个宏用户(Macro User, MU);毫微蜂窝网络由1个毫微基站(FBS)和(K+1)个毫微用户(FU)组成,均具有FD通信能力,其中FBS配有Nt(Nt>K)根发射天线和Nr根接收天线,每个FU配备2根天线。图 1的模型着重考虑毫微蜂窝的通信安全性,因此当合法FU与FBS通信时,其余K个非合法FU均可视为潜在的窃听者(Eve),即毫微蜂窝中包含1个FBS、1个合法FU以及K个Eve。
|
| 图 1 多窃听全双工两层异构无线携能通信网络架构 Fig. 1 Multi eavesdropping two-layer FD-SWIPT-HCN architecture |
为了确保合法用户的机密信息不被窃听,FBS通过在发射信号中添加AN并通过相应的BM设计提升通信安全性。为了克服移动终端设备有限电池容量所带来的局限性,毫微蜂窝中的用户采用基于PS的SWIPT技术,将收到的RF信号分为ρ和1-ρ两部分(ρ为FU信息解码的功率分流系数),分别用于信息解码以及收集能量为自身供电以延长生命周期。此外,由于FD通信产生的自干扰对于能量收集场景是有益的,因此终端用户用于EH的信号也包括产生的自干扰信号。
那么,FBS发射的信号x为
| $ \boldsymbol{x}=\boldsymbol{\omega} s^{D L}+\boldsymbol{z}, $ | (1) |
其中,ω为下行信息信号波束成形矢量;z为嵌入的下行AN矢量;sDL为FBS发送给FU的下行信息信号,满足期望值E{|sDL|2}=1。
上、下行传输同时进行的FD通信场景中的UL传输阶段FBS收到的信号yFUL可表示为
| $ \begin{aligned} & \quad y_F^{U L}=\sqrt{p_u} \boldsymbol{v}^H \boldsymbol{h}_{F U, F} s^{U L}+\sqrt{\alpha} \boldsymbol{v}^H \boldsymbol{L}_F\left(\boldsymbol{\omega} s^{D L}+\boldsymbol{z}\right)+ \boldsymbol{I}_M+\boldsymbol{n}_b+\boldsymbol{n}_p, \end{aligned} $ | (2) |
其中,pu为FU的上行发射功率,hFU, F为FU到FBS之间的信道系数,FU发送的上行信息信号为sUL,满足期望值E{|sDL|2}=1。α表示FBS处的残余自干扰,LF为FBS的自干扰信道增益矩阵。由于毫微蜂窝覆盖范围较小且相距MBS较远,因此将来自MBS的干扰视为常量,用IM表示。nb、np分别表示FBS处的背景噪声及信号处理产生的噪声,vH为上行接收波束成形矢量。
式(2)右侧第1项为FBS接收到的FU发射的信息信号,第2项为FBS全双工对自身产生的自干扰信号。
FBS采用文献[27]的最大比合并(Maximum Ratio Combination,MRC)策略接收信号,其中的上行接收波束成形矢量v为
| $ v=\frac{\boldsymbol{h}}{\|\boldsymbol{h}\|} . $ | (3) |
上行传输的信干噪比SINRUL为
| $ \mathit{SINR}_{U L}=\frac{p_u\left\|\boldsymbol{v}^H \boldsymbol{h}_{F U, F}\right\|^2}{\alpha \|\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{\omega}+\boldsymbol{z}) \|^2+\varepsilon^2+\sigma_b^2+\sigma_p^2\right.} 。$ | (4) |
根据香农定理,上行传输速率RUL为
| $ R_{U L}=B \log _2\left(1+S I N R_{U L}\right) \text。$ | (5) |
下行传输阶段,FU收到的信号为
| $ y_{F U}^{D L}=\boldsymbol{h}_{F, F U}\left(\boldsymbol{\omega} s^{D L}+\boldsymbol{z}\right)+\sqrt{\boldsymbol{\beta}} \sqrt{\boldsymbol{p}_u} \boldsymbol{l}_{F U} s^{U L}+\boldsymbol{I}_M+\boldsymbol{n}_{b}, $ | (6) |
式(6)右侧第1项为FU期望从FBS获得的信息信号以及FBS发射的AN带来的干扰,第2项为自干扰,第3项为来自MBS的跨层干扰,最后一项为背景噪声。其中,β表示FU处的残余自干扰,lFU为FU处的自干扰信道系数。
经过功率分流后FU用于ID和EH的信号分别为
| $ y_{F U}^{I D}=\sqrt{\rho} y_{F U}^{D L}+\boldsymbol{n}_p, $ | (7) |
| $ y_{F U}^{E H}=\sqrt{1-\rho} y_{F U \circ}^{D L} $ | (8) |
因此,下行传输的信干噪比为
| $ \mathit{SINR}_{D L}=\frac{\rho\left\|\boldsymbol{h}_{F, F U} \boldsymbol{\omega}\right\|^2}{\rho\left(\left\|\boldsymbol{h}_{F, F U} \boldsymbol{z}\right\|^2+\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\sigma_b^2\right)+\sigma_p^2} 。$ | (9) |
根据香农定理,下行传输速率为
| $ R_{D L}=B \log _2\left(1+S I N R_{D L}\right) 。$ | (10) |
根据本研究建立的信号传输模型,Evek收到的信号为
| $ y_{\mathrm{Eve}_k}=\boldsymbol{g}_k \boldsymbol{\omega} s^{D L}+\sqrt{p_u} \boldsymbol{q}_k s^{U L}+\boldsymbol{g}_k \boldsymbol{z}+\boldsymbol{I}_M+\boldsymbol{n}_b+\boldsymbol{n}_p, $ | (11) |
式(11)等号右侧的第1项和第2项分别为FBS和FU发送的机密信息信号,第3项为AN干扰信号,最后3项分别为跨层干扰信号、背景噪声以及信号处理引入的噪声。其中,gk为FBS到Evek之间的信道增益,qk为FU到Evek之间的信道增益。
根据文献[28]的多信道接入的容量计算方式和文献[29]的研究结果,Evek处的信干噪比为
| $ S I N R_{\mathrm{Eve}_k}=\frac{\left\|\boldsymbol{g}_k \boldsymbol{\omega}\right\|^2+p_u\left\|\boldsymbol{q}_k\right\|^2}{\left\|\boldsymbol{g}_k \boldsymbol{z}\right\|^2+\varepsilon^2+\sigma_b^2+\sigma_p^2}。$ | (12) |
根据香农定理,则Evek的速率为
| $ R_{\mathrm{Eve}_k}=B \log _2\left(1+S I N R_{\mathrm{Eve}_k}\right) 。$ | (13) |
系统的可达安全速率取决于用户信道容量与窃听者信道容量之差,根据最坏情况准则,系统的最小安全速率取决于窃听能力最强的节点,因此系统的安全速率为
| $ R_S=\left[R_{U L}+R_{D L}-R_{\mathrm{Eve}_k}^{wst}\right]^{+}, $ | (14) |
其中,REvekwst=max{REvek|k=1, …, K},[x]+表示max(0, x)。
本研究假设FU具有自能量回收能力,因此根据式(8)可知,FU收集到的能量为
| $ \begin{aligned} & E_{E H}=\xi(1-\rho)\left(\left\|\boldsymbol{h}_{F, F U}(\boldsymbol{\omega}+\boldsymbol{z})\right\|^2+\right.\left.\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\sigma_b^2\right), \end{aligned} $ | (15) |
其中,ξ为EH电路的能量转换效率。
通过EH技术收集到的能量可以补偿一定的系统能耗,因此整个毫微蜂窝消耗的能量为
| $ Q_{t o t}=\tau\left(\|\boldsymbol{w}+\boldsymbol{z}\|^2+p_u\right)+P_C-E_{E H}, $ | (16) |
式(16)右侧第1项为FBS和FU发射信号消耗的能量,第2项为系统电路的静态功耗,第3项为通过SWIPT收集到的能量。其中τ为功率放大器的效率。
综上,系统的能量效率为
| $ S E E=\frac{R_S}{Q_{t o t}} 。$ | (17) |
根据通信服务质量的需求,以及对人体辐射安全的要求,需要对安全传输速率和基站的发射功率等进行约束。综上所述,系统的SEE资源分配问题(P1)可以表示为
| $ \text { P1: } \mathop {{\rm{max}}}\limits_{\left\{ {w,z.p\left. {_u} \right\}} \right.} \eta_{E E}=\frac{R_S}{Q_{t o t}}, $ | (18) |
| $ \text { s.t. } \quad \mathrm{C} 1: R_S \geqslant R_{\min } \text {, } $ | (19) |
| $ \mathrm{C} 2:\|\boldsymbol{w}+\boldsymbol{z}\|^2 \leqslant P_{F^{\max }}, $ | (20) |
| $ \mathrm{C} 3:\left\|f_m(\boldsymbol{w}+\boldsymbol{z})\right\|^2 \leqslant I_{t h}, $ | (21) |
| $ \mathrm{C} 4: E_{E H} \geqslant E_{\min }, $ | (22) |
| $ \mathrm{C} 5: 0 \leqslant p_u \leqslant P_{U^{\max }}, $ | (23) |
其中,式(18)为优化问题的目标函数;式(19)保证系统的安全传输速率不低于FU最小安全传输速率Rmin;式(20)约束了FBS的发射功率,其中的PFmax为FBS最大发射功率,ω为下行信息信号波束成形矢量,z为嵌入的下行人工噪声矢量;式(21)约束了FBS发射功率对靠近毫微蜂窝小区的MU的干扰,其中的fm(m=1, …, M)为FBS与MUm之间的信道系数,Ith为FBS对宏蜂窝的干扰阈值;式(22)要求FU通过EH技术收集到的能量不低于最低收集能量阈值Emin;式(23)则对FU的发射功率做出相应的约束,其中的PUmax为FU上行最大发射功率。
w和z的二次存在形式导致约束项的非凸性,根据半定松弛方案,可以定义W=wwH,Z=zzH作为新的优化变量,且需满足W
| $ \mathrm{P} 2: \mathop {\max }\limits_{\{ \boldsymbol{W},\boldsymbol{Z.}{P_{_u}}\} } \eta_{E E}=\frac{R_S}{Q_{t o t}}, $ | (24) |
| $ \text { s. t. } \quad \mathrm{C} 1: R_S \geqslant R_{\min } \text {, } $ | (25) |
| $ \mathrm{C} 2: \mathit{Tr}(\boldsymbol{W}+\boldsymbol{Z}) \leqslant P_{F^{\max }}, $ | (26) |
| $ \begin{aligned} & \mathrm{C} 3: \mathit{Tr}\left(f_m^H(\boldsymbol{W}+\boldsymbol{Z}) f_m\right) \leqslant I_{t h}, \end{aligned} $ | (27) |
| $ \begin{aligned} & \mathrm{C} 4: E_{E H} \geqslant E_{\min }, \end{aligned} $ | (28) |
| $ \begin{aligned} & \mathrm{C} 5: 0 \leqslant p_u \leqslant P_{U^{\max }}, \end{aligned} $ | (29) |
| $ \begin{aligned} & \mathrm{C} 6: \boldsymbol{W}\succ0, \boldsymbol{Z}\succ0, \end{aligned} $ | (30) |
| $ \begin{aligned} & \mathrm{C} 7: \operatorname{rank}(\boldsymbol{W})=1, \operatorname{rank}(\boldsymbol{Z})=1, \end{aligned} $ | (31) |
其中,EEH=ξ(1-ρ)(Tr(hF, FU(W+Z)hF, FU)+βpu‖lFU‖2+ε2+σb2)。
2.2 非凸分式规划优化问题P2的分式目标函数以及相互耦合的优化变量使得该问题成为一个非凸分式规划问题。为此,首先利用Dinkelbach方法将原分式目标函数转化为等价的参数相减形式。假设系统的最优能效值为ηEE*,则P2的目标函数可以被等价转化为
| $ F\left(\eta_{E E}\right)=\max \left\{R_S-\eta_{E E} Q_{t o t}\right\}_。$ | (32) |
利用Dinkelbach法并去掉秩一约束C7,优化问题P2可转化为如下形式的优化问题
| $ \mathrm{P} 3: \max R_S-\eta_{E E} Q_{\text {tot }}, $ | (33) |
| $ \text { s. t. } \mathrm{C} 1: R_S \geqslant R_{\min }, $ | (34) |
| $ \mathrm{C} 2: \mathit{Tr}(\boldsymbol{W}+\boldsymbol{Z}) \leqslant P_{F^{\max }}, $ | (35) |
| $ \mathrm{C} 3: \mathit{Tr}\left(f_m^H(\boldsymbol{W}+\boldsymbol{Z}) f_m\right) \leqslant I_{t h}, $ | (36) |
| $ \mathrm{C} 4: E_{E H} \geqslant E_{\min }, $ | (37) |
| $ \mathrm{C} 5: 0 \leqslant p_u \leqslant P_{U^{\max }}, $ | (38) |
| $ \mathrm{C} 6: \boldsymbol{W} \succ 0, \boldsymbol{Z} \succ 0 $ | (39) |
根据文献[30],当且仅当满足以下条件时转化后的问题P3与原问题P2的解等价。即
| $ \begin{gathered} F\left(\eta_{E E}^*\right)=\max \left\{R_S-\eta_{E E} Q_{t o t}\right\}=R_S\left(\boldsymbol{W}^*, \boldsymbol{Z}^*\right., \left.\left.p_u^*\right)-\eta_{E E}^* Q_{t o t}\left(\boldsymbol{W}^*, \boldsymbol{Z}^*, p_u^*\right)\right\}=0 \end{gathered} $ | (40) |
利用Dinkelbach方法将原问题转化为参数相减的形式后,通过迭代法可以不断逼近原问题的最优解,基于Dinkelbach的外层循环迭代的主要流程如下。
Step1:初始化迭代次数t=0,能效初值ηEE(t)=0,收敛精度ε>0。
Step2:求解问题P3得到F(ηEE(t)),并更新ηEE(t)=RS(t)/Qtot(t),t=t+1。
Step3:若|ηEE(t)-ηEE(t-1)|≤ε,即满足收敛精度要求则结束迭代,输出最优值F(ηEE*);否则转至Step2继续迭代。
在Step2中,由于W, Z, pu的耦合使得问题P3仍然非凸难以求解,因此需要先将其转化为易于求解的凸优化问题形式,具体的求解过程将在2.3节详细阐述。此外,为解决优化问题的非凸性,在将问题转换为P3的过程中利用半定松弛技术舍弃了秩一约束条件C7。若通过求解优化问题获得的解W, Z满足rank(W)=1, rank(Z)=1,则可以认为所得到的解即为未省略C7的解,最后通过特征值分解W=wwH,Z=zzH得到对应的信息信号和AN波束成形矢量w、z,否则可以通过高斯随机优化过程获得近似解。
2.3 连续凸近似在原优化问题中,优化变量同时存在于保密速率表达式的分子、分母中且相互耦合,这导致了原优化问题的非凸性,使得问题无法直接求解。为此,本小节提出一种基于泰勒展开的SCA求解方法。具体来说,首先引入松弛变量替换存在耦合变量的速率表达式,然后基于一阶泰勒展开将非凸函数转换为其对应的近似凸函数,最后通过迭代求解逐渐逼近原非凸问题的最优解。
由式(5)、(10)、(13)可知
| $ R_{U L}=B \log _2\left(1+\frac{p_u\left\|\boldsymbol{v}^H \boldsymbol{h}_{F U, F}\right\|^2}{\alpha \operatorname{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2}\right), $ | (41) |
| $ R_{D L}=B \log _2\left(1+\frac{\rho \mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{W} \boldsymbol{h}_{F, F U}\right)}{\rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)+\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\sigma_b^2\right)+\sigma_p^2}\right), $ | (42) |
| $ R_{\mathrm{Eve}_k}=B \log _2\left(1+\frac{\mathit{Tr}\left(\boldsymbol{g}_k^H \boldsymbol{W} \boldsymbol{g}_k\right)+p_u\left\|\boldsymbol{q}_k\right\|^2}{\mathit{Tr}\left(\boldsymbol{g}_k^H \boldsymbol{Z} \boldsymbol{g}_k\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2}\right) 。$ | (43) |
首先为保密速率表达式中的分子和分母引入下列松弛变量:
| $ \begin{aligned} & \quad e^{r n}=p_u\left\|\boldsymbol{v}^H \boldsymbol{h}_{F U, F}\right\|^2+\alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+ \varepsilon^2+\sigma_b^2+\sigma_p^2, \end{aligned} $ | (44) |
| $ e^{r d}=\alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2, $ | (45) |
| $ \begin{aligned} & \quad e^{s n}=\rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H(\boldsymbol{W}+\boldsymbol{Zh})\boldsymbol{h}_{F, F U}\right)+\right. \left.\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\sigma_b^2\right)+\sigma_p^2, \end{aligned} $ | (46) |
| $ \begin{aligned} & e^{s d}=\rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)+\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\right.\left.\sigma_b^2\right)+\sigma_p^2, \end{aligned} $ | (47) |
| $ \begin{aligned} & \quad e^{t n}=\mathit{Tr}\left(\boldsymbol{g}_k^H(\boldsymbol{W}+\boldsymbol{Z}) \boldsymbol{g}_k\right)+p_u\left\|\boldsymbol{q}_k\right\|^2+\varepsilon^2+ \sigma_b^2+\sigma_p^2, \end{aligned} $ | (48) |
| $ \begin{aligned} e^{t d}=\mathit{Tr}\left(\boldsymbol{g}_k^H \boldsymbol{Z} \boldsymbol{g}_k\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2, \end{aligned} $ | (49) |
其中,ern, erd, esn, esd, etn, etd为引入的松弛变量。
通过将式(44)-(49)代入式(33),优化问题P3可以松弛为以下问题。
| $ \begin{aligned} & \mathrm{P} 4: \max \left\{(m-r d+s n-s d+t d-t n) B \log _2 e-\right.\left.\eta_{E E} Q_{t o t}\right\} \end{aligned} $ | (50) |
| $ \begin{aligned} & \text { s. t. } \quad \overline{\mathrm{C} 1}:(r n-r d+s n-s d+t d- \text { tn) } B \log _2 e \geqslant R_{\min }, \end{aligned} $ | (51) |
| $ \mathrm{C} 2, \mathrm{C} 3, \mathrm{C} 4, \mathrm{C} 5, \mathrm{C} 6 $ | (52) |
| $ \begin{aligned} & \mathrm{C} 8: p_u\left\|\boldsymbol{v}^H \boldsymbol{h}_{F U, F}\right\|^2+\alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+ \varepsilon^2+\sigma_b^2+\sigma_p^2 \geqslant e^{r n}, \end{aligned} $ | (53) |
| $ \mathrm{C} 9: \alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2 \geqslant e^{r d}, $ | (54) |
| $ \begin{aligned} &\mathrm{C} 10: \rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{W} \boldsymbol{h}_{F, F U}\right)+\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)+\right.\left.\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\sigma_b^2\right)+\sigma_p^2 \geqslant e^{s n}, \end{aligned} $ | (55) |
| $ \begin{aligned} & \mathrm{C} 11: \rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)+\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\right. \left.\sigma_b^2\right)+\sigma_p^2 \geqslant e^{s d}, \end{aligned} $ | (56) |
| $ \begin{aligned} & \quad \mathrm{C} 12: \mathit{Tr}\left(\boldsymbol{g}_k^H(\boldsymbol{W}+\boldsymbol{Z}) \boldsymbol{g}_k\right)+p_u\left\|\boldsymbol{q}_k\right\|^2+\varepsilon^2+ \sigma_b^2+\sigma_p^2 \geqslant e^{t n}, \end{aligned} $ | (57) |
| $ \mathrm{C} 13: \mathit{Tr}\left(\boldsymbol{g}_k^H \boldsymbol{Z} \boldsymbol{g}_k\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2 \geqslant e^{t d} 。$ | (58) |
P4的目标函数以及约束C1均被松弛变量所替换,并增加了6个关于松弛变量的约束条件C8-C13。由于目标函数的单调性,这6个约束条件将在最优时相等。松弛后,约束条件C9、C11、C12仍然非凸,优化问题P4仍难以求解。运用SCA思想,对于这几个非凸约束,首先找到其近似函数,再通过在其线性逼近点处迭代更新逐渐逼近非凸约束。考虑到指数函数在某确定点处一阶泰勒展开可得到其局部紧的线性近似函数的性质,下面分别对{erd,esd,etn}进行一阶泰勒展开,得到它们在线性逼近非凸约束的点{rd, sd, tn }处满足局部紧的下界,以此逼近这些非凸约束。对非凸约束中的松弛变量{erd,esd,etn}分别在某确定点{rd, sd, tn }处进行一阶泰勒展开,可得到
| $ \begin{aligned} & e^{r d} \geqslant e^{\overline{r d}}(r d-\overline{r d}+1) \\ & e^{s d} \geqslant e^{\overline{s d}}(s d-\overline{s d}+1), \\ & e^{t n} \geqslant e^{\overline{t n}}(t n-\overline{t n}+1) \end{aligned} $ | (59) |
其中,{rd, sd, tn }是线性逼近非凸约束的点。
将式(59)代入非凸约束C9、C11、C12,可以得到
| $ \begin{aligned} & \quad \overline{\mathrm{C} 9}: \alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2 \leqslant \left.e^{\overline{r d}}(r d- \overline{r d}+1\right) \\ & \overline{\mathrm{C} 11}: \rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)+\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\right. \left.\sigma_b^2\right)+\sigma_p^2 \leqslant e^{\overline{s d}}(s d-\overline{s d}+1) \\ & \overline{\mathrm{C} 12}: \mathit{Tr}\left(\boldsymbol{g}_k^H(\boldsymbol{W}+\boldsymbol{Z}) \boldsymbol{g}_k\right)+p_u\left\|\boldsymbol{q}_k\right\|^2+\varepsilon^2+ \sigma_b^2+\sigma_p^2 \leqslant e^{\overline{t n}}(t n-\overline{t n}+1) 。\end{aligned} $ | (60) |
因此,将式(60)代入优化问题P4,最终被等价转换为
| $ \begin{aligned} & \mathrm{P} 5: \max \left\{(m-r d+s n-s d+t d-t n) B \log _2 e-\right. \left.\eta_{E E} Q_{t o t}\right\}, \end{aligned} $ | (61) |
| $ \begin{aligned} & \text { s. t. } \overline{\mathrm{C} 1:}(r n-r d+s n-s d+t d-t n) B \log _2 e \geqslant R_{\min }, \end{aligned} $ | (62) |
| $ \mathrm{C} 2, \mathrm{C} 3, \mathrm{C} 4, \mathrm{C} 5, \mathrm{C} 6 $ | (63) |
| $ \begin{aligned} & \quad \mathrm{C} 8: p_u\left\|\boldsymbol{v}^H \boldsymbol{h}_{F U, F}\right\|^2+\alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+ \varepsilon^2+\sigma_b^2+\sigma_p^2 \geqslant e^{r n}, \end{aligned} $ | (64) |
| $ \begin{aligned} & \overline{\mathrm{C} 9}: \alpha \mathit{Tr}\left(\boldsymbol{v}^H \boldsymbol{L}_F(\boldsymbol{W}+\boldsymbol{Z})\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2 \leqslant e^{\overline{e d}}(r d-\overline{r d}+1), \end{aligned} $ | (65) |
| $ \begin{aligned} &\mathrm{C10}: \rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{W} \boldsymbol{h}_{F, F U}\right)+\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)\right.+ \left.\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\sigma_b^2\right)+\sigma_p^2 \geqslant e^{s n}, \end{aligned} $ | (66) |
| $ \begin{aligned} \overline{\mathrm{C} 11}: \rho\left(\mathit{Tr}\left(\boldsymbol{h}_{F, F U}^H \boldsymbol{Z} \boldsymbol{h}_{F, F U}\right)+\beta p_u\left\|\boldsymbol{l}_{F U}\right\|^2+\varepsilon^2+\right. \left.\sigma_b^2\right)+\sigma_p^2 \leqslant e^{\overline{s d}}(s d-\overline{s d}+1), \end{aligned} $ | (67) |
| $ \begin{aligned} & \quad \overline{\mathrm{C} 12}: \mathit{Tr}\left(\boldsymbol{g}_k^H(\boldsymbol{W}+\boldsymbol{Z}) \boldsymbol{g}_k\right)+p_u\left\|\boldsymbol{q}_k\right\|^2+\varepsilon^2+ \sigma_b^2+\sigma_p^2 \leqslant e^{\overline{t n}}(t n-\overline{t n}+1), \end{aligned} $ | (68) |
| $ \mathrm{C} 13: \mathit{Tr}\left(\boldsymbol{g}_k^H \boldsymbol{Z} \boldsymbol{g}_k\right)+\varepsilon^2+\sigma_b^2+\sigma_p^2 \geqslant e^{t d} \text { 。} $ | (69) |
显然,经过一系列松弛转化后得到的优化问题P3是一个凸优化问题,可以通过连续凸近似算法以及MATLAB的凸优化工具箱CVX进行求解。
SCA算法可以描述为以下4个步骤:
Step1:初始化W(0),Z(0),pu(0)以及近似点的可行初始值{erd, esd, etn}(0)。
Step2:在给定点{erd, esd, etn}(n)使用CVX工具箱求解问题P5,得到一组新的W(n),Z(n),pu(n)解。
Step3:用新的解更新近似点{erd, esd, etn}(n+1)的值。
Step4:若满足收敛精度要求则结束迭代,对W*,Z*,pu*进行秩一分解得到最优解w*,z*,pu*,否则转至Step2。
2.4 算法描述综合上述分析,本小节为FD异构SWIPT网络SEE最大化提出了一种基于AN辅助的联合波束成形设计方案和相应的算法,首先外层循环利用Dinkelbach方法将非凸分式规划问题转换为参数相减的形式,其次在内层循环中利用基于泰勒展开的连续凸近似方法对优化变量进行解耦并求解。这一基于Dinkelbach和SCA的双层波束成形优化算法的详细步骤描述如下:
算法1基于Dinkelbach和SCA的双层波束成形优化算法
输入:ηEE(t)=0,W(0),Z(0),pu(0),{erd, esd, etn}(0)
输出:w*,z*,pu*,ηEE*
1) 初始化参数:各项物理参数;迭代次数t=0,能效初值ηEE(t)=0,收敛精度ε>0;
2) While t≤maxiter1或|ηEE(t)- ηEE(t-1)| >ε初始化W(0),Z(0),pu(0),以及近似点的可行初始值{erd, esd, etn}(0)
3) for all Eves根据式(4)-(13)计算速率并找到窃听能力最强的节点
4) While l≤maxiter2或|ηEE(t)- ηEE(t-1)|>ε|ei(n)-ei(n-1)|>ε(i=rd, sd, tn)
5) 在给定点{erd, esd, etn}(n)求解问题P5得到新的解W(n),Z(n),pu(n)
6) 利用步骤5)得到的值更新近似点{erd, esd, etn}(n+1)的值。
7) 计算该次迭代得到的RS(n), ηEE(n), Qtot(n);
8) n=n+1;
9) end while
10) 计算F(ηEE(t)=RS(n-1)-ηEE(n1)Qtot(n-1);
11) 更新ηEE(t+1)=RS(n-1)/Qtot(n-1),t=t+1;
12) end while
13) 通过对W*,Z*秩一分解得到w*,z*
输出:w*,z*,pu*,ηEE*
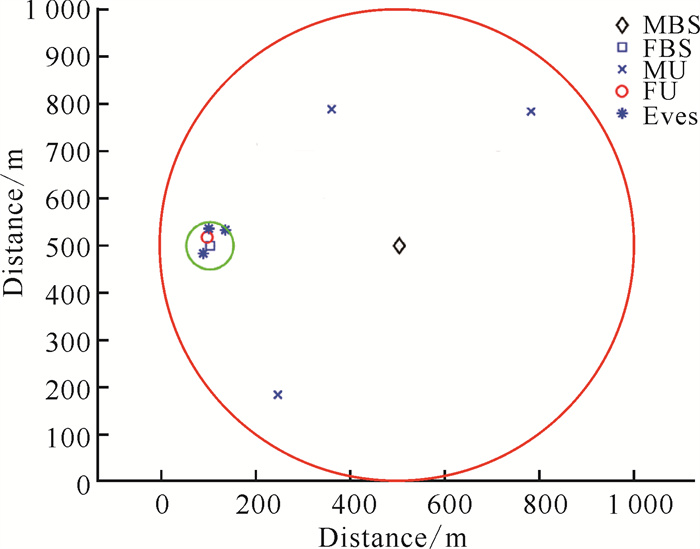
3 仿真实验及结果分析 3.1 实验环境与参数设置仿真实验是在一台微机上采用R2018b版本的MATLAB仿真软件实现的。首先模拟并生成两层异构蜂窝网络通信场景(图 2),MBS的通信半径设置为500 m,在其覆盖范围内随机分布着一定数量的宏用户,FBS随机分布在宏蜂窝的边缘地区,FBS的覆盖范围半径为30 m,在FBS内部随机生成毫微用户和窃听者。为便于计算,本节设定宏蜂窝中有3个宏用户(MU),毫微蜂窝中包含1个毫微用户(FU),3个窃听者(Eve),假设各通信节点之间的信道系数独立同分布,且服从瑞利分布。其次设置优化问题中约束条件涉及到的相关阈值,用于算法中的初始化及物理参数设定。最后通过本研究所提出的算法求解优化问题。
|
| 图 2 两层异构蜂窝网络无线携能通信网络场景 Fig. 2 Two-layer FD-SWIPT-HCN architecture |
仿真参数设置如下:FBS发射天线数量Nt=4,FBS接收天线数量Nr=4,FBS发射功率阈值PFmax=10 W,FU发射功率阈值PUmax=0.5 W,静态电路功耗PC=10 W,干扰功率阈值Ith=0.05 W,最小安全传输速率Rmin=3 bps,高斯白噪声nb=-50 dBm,信号处理噪声np=-60 dBm,带宽为1 MHz,载波频率为2 GHz,能量转换效率ξ=0.8。
3.2 仿真实验结果分析仿真实验是为了验证本研究方案的有效性、收敛性与优越性。具体来说,将本研究方案与以下几种方案进行对比:1)将本研究所提FD通信场景与TDD、FDD通信场景进行性能对比,说明本研究方案在系统SEE方面的优越性;2)在相同的FD和TDD通信场景下,将本研究方案与TDD-AN辅助方案[15]、ZF波束成形方案以及无AN辅助方案的SEE性能进行对比,以验证本研究方案的有效性和优越性。
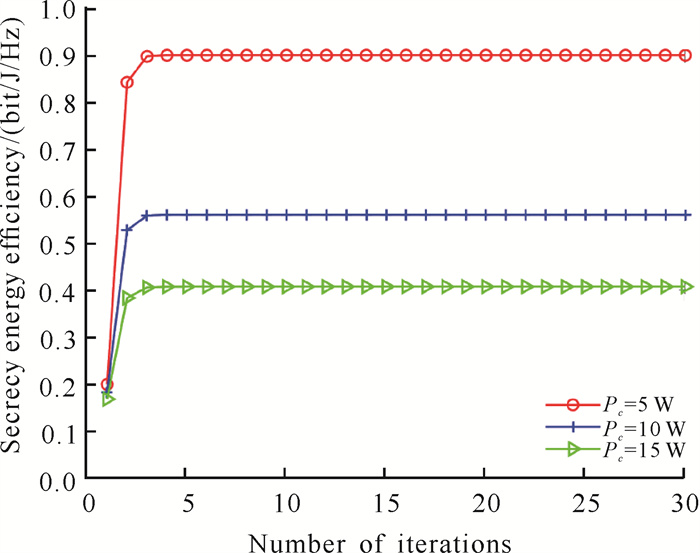
3.2.1 本研究方案的有效性和收敛性分析首先验证本研究方案对应优化算法的收敛性。图 3为不同静态功耗下SEE的收敛情况,可以看出在给定的不同静态功耗条件下,算法迭代6次后就能收敛,收敛性能好。此外,随着电路静态功耗的增加,SEE显著降低,说明在实际移动通信中应该注重对系统电路硬件、设备运行等进行优化,以达到减小静态功耗、提升能量效率的目的。
|
| 图 3 不同静态功耗下SEE随迭代次数收敛 Fig. 3 Convergence of SEE with the increase in iterations under different static power consumption |
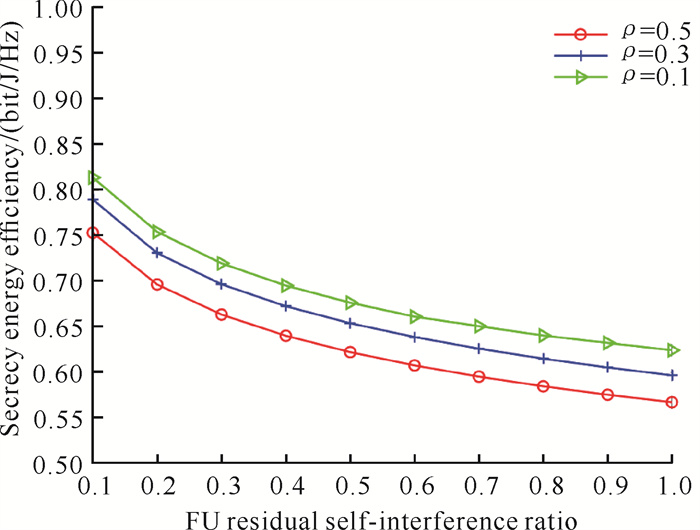
图 4给出了自干扰消除能力对SEE的影响,横坐标为残余自干扰比例。从图 4可以看出,残余自干扰比例越高,系统的SEE性能越差。这是因为FD产生的自干扰信号对传输速率有较大影响,当接收天线处无法进行有效的自干扰消除时,过大的自干扰信号会导致用户的SINR条件恶化,对传输速率有较大的影响,而较强的自干扰消除能力则能够削弱自干扰信号,提升信干噪比从而使得传输速率显著增长,进而使得SEE得到提升。
|
| 图 4 自干扰消除能力对SEE的影响 Fig. 4 Influence of self-interference cancellation on SEE |
3.2.2 本研究方案的有效性和优越性分析
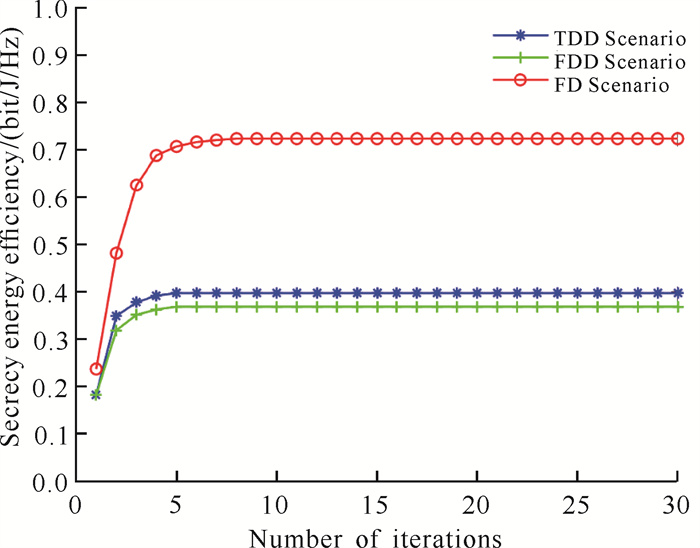
图 5将本研究所提的具有自能量回收的FD通信场景分别与TDD、FDD通信场景进行性能对比,验证了FD通信场景的优越性。实验结果表明,FD通信场景的SEE性能表现明显优于另外两种双工技术。尽管FD通信模式增加了自干扰以及少量的系统能耗,但是其对频谱和时间接近2倍的利用率提升为传输速率带来了大幅增益。这说明通过有效的自干扰消除手段,FD系统可以实现显著的SEE性能增益。由图 5可知,TDD的效果略优于FDD,因此,后续的方案对比实验着重将本研究所提AN辅助方案(简记为FD-AN)与ZFAN辅助方案[15]以及无AN辅助方案分别在FD和TDD模式下进行SEE的性能对比分析。在实验图中,FD模式下的ZFAN辅助方案简记为FD-ZFAN, FD模式下的无AN辅助方案简记为FD-noAN,TDD模式下的ZFAN辅助方案简记为TDD-ZFAN, TDD模式下的无AN辅助方案简记为TDD-noAN。
|
| 图 5 不同方案下SEE随迭代次数收敛 Fig. 5 Convergence of SEE with the increase in iterations under different schemes |
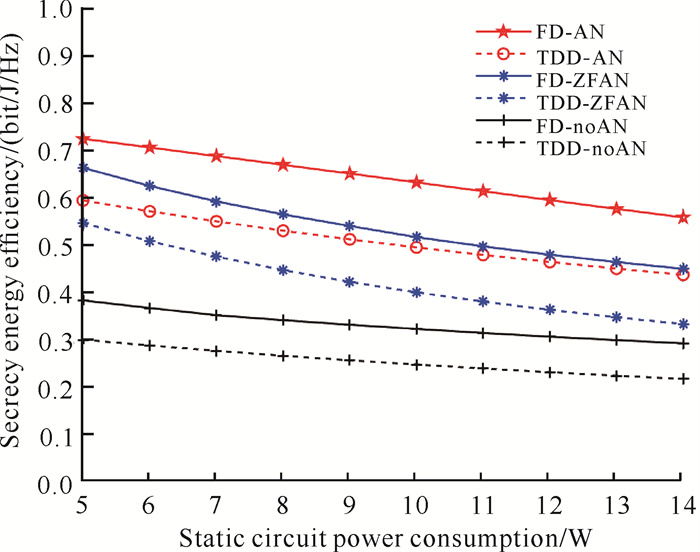
由图 6可知,不同方案中SEE均随静态电路功耗的增加而减小。当静态电路功耗相同时,本研究所提方案的SEE显著高于另外5种方案。无论是FD还是TDD模式,无AN辅助的方案安全性能最差,一是因为缺少了AN对窃听者的干扰,窃听者处的信干噪比相对较高,导致系统的安全速率降低;二是为了达到安全传输目的所增大的发射功率会加剧系统对能量的消耗,二者共同导致了SEE的降低。该结果充分说明AN辅助在削弱窃听节点能力、提升传输安全方面的有效性。此外,本研究所提FD-AN辅助算法的性能也优于对比方案3,这是因为方案3中AN处于合法用户的零空间中,但对于窃听节点不具有指向性,无法根据通信情况做出适应的调整,对窃听节点的干扰较差,因此其SEE略低于本研究所提方案。
|
| 图 6 不同静态功耗下不同方案的SEE对比 Fig. 6 Influence of static power consumption under different schemes on SEE |
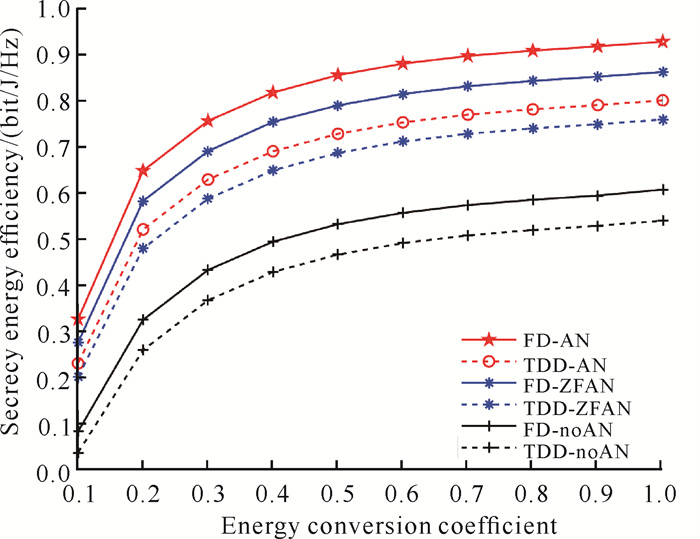
图 7给出了不同方案下能量转换效率ξ对系统SEE的影响。由图 7可知,当能量转换效率相同时,本研究所提出的AN辅助算法的SEE始终优于其他方案。所有方案的SEE均随能量转换效率的增大而增大,能量转换效率ξ的提高有益于提高SEE,这是因为ξ的提高代表节点转化收集能量的能力增强,能够更好地补偿系统能耗,因而有助于SEE的提升。此外,SEE随ξ的增长趋势并非线性,当ξ>0.5后,ξ继续增大对SEE的增益趋势不太明显,据此在实际应用中,可适当放宽对实现RF信号—电能能量转换器件硬件的要求。
|
| 图 7 不同方案下能量转换效率对SEE的影响 Fig. 7 Influence of energy conversion efficiency on SEE |
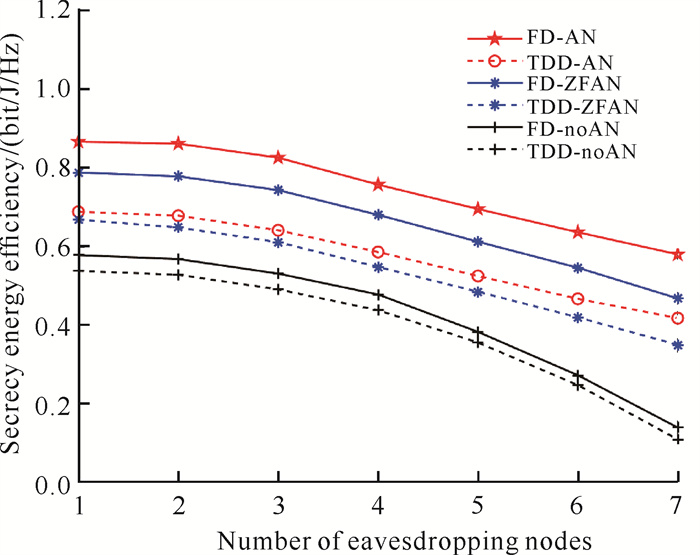
图 8给出了窃听节点个数对系统SEE的影响。从图 8中可以看到,随着窃听节点数量的增多,6种方案的安全性能均有所降低,且当窃听节点数量超过3个时,系统安全性能下降的幅度逐渐增大。本研究所提出的AN辅助方案相较于其他5种方案,SEE的下降幅度最缓,无AN辅助的方案安全性能下降幅度最大。这是因为AN辅助可以削弱窃听者处的信干噪比,降低其窃听信息的能力或增大其窃听信息的代价。综上,当通信条件恶化时,相较于其他方案,本研究所提方案仍然具有较好的抵抗风险能力。
|
| 图 8 不同方案下窃听节点个数对SEE的影响 Fig. 8 Influence of the number of eavesdropping nodes on SEE |
4 结论
能量效率和传输安全是SWIPT系统中十分重要的研究课题。本研究考虑存在多个窃听节点的通信场景,在满足通信服务质量要求、安全发射功率阈值以及能量收集等约束条件的前提下,以系统SEE优化为目标,提出了一种基于AN辅助的FD异构SWIPT网络安全波束成形设计方案和一种基于Dinkelbach和SCA的双层资源分配优化算法。其主要思路: 首先对问题进行分析并数学建模,得到一个非凸分式优化问题;然后利用Dinkelbach法将原分式问题转化为参数相减形式,再通过半定松弛技术、泰勒级数展开、连续凸近似法将难以求解的原始非凸分式规划问题进行等价的转换和松弛,得到易于求解的凸优化问题;最后利用MATLAB软件中的凸优化工具箱CVX进行求解。仿真实验验证了本研究所提的具有自能量回收的FD异构SWIPT场景、具有AN辅助的安全波束成形方案和双层资源分配优化算法的优越性。
| [1] |
马忠贵, 宋佳倩. 5G超密集网络的能量效率研究综述[J]. 工程科学学报, 2019, 41(8): 968-980. |
| [2] |
MARANDI L, NASLCHERAGHI M, ALI GHORASHI S, et al. Delay analysis in full-duplex heterogeneous cellular networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(10): 9713-9721. DOI:10.1109/TVT.2019.2932191 |
| [3] |
李陶深, 施安妮, 王哲, 等. 基于SWIPT的吞吐量最优化NOMA全双工中继选择策略[J]. 通信学报, 2021, 42(5): 87-97. |
| [4] |
王哲, 李陶深, 叶进, 等. 能量收集网络技术研究与发展[J]. 广西科学, 2019, 26(3): 253-266, 355. DOI:10.13656/j.cnki.gxkx.20190618.006 |
| [5] |
CLERCKX B, ZHANG R, SCHOBER R, et al. Fundamentals of wireless information and power transfer: from RF energy harvester models to signal and system designs[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(1): 4-33. DOI:10.1109/JSAC.2018.2872615 |
| [6] |
李陶深, 朱晴, 王哲, 等. 基于5G的无线携能通信技术研究综述[J]. 广西科学, 2021, 28(3): 229-241. DOI:10.13656/j.cnki.gxkx.20210830.012 |
| [7] |
CHEN D H, HE Y C. Full-duplex secure communications in cellular networks with downlink wireless power transfer[J]. IEEE Transactions on Communications, 2018, 66(1): 265-277. DOI:10.1109/TCOMM.2017.2756884 |
| [8] |
VIET TUAN P, NGOC SON P, TRUNG DUY T, et al. Optimizing a secure two-way network with non-linear SWIPT, channel uncertainty, and a hidden eavesdropper[J]. Electronics, 2020, 9(8): 1222. DOI:10.3390/electronics9081222 |
| [9] |
MA H, CHENG J L, WANG X F. Proportional fair secrecy beamforming for MISO heterogeneous cellular networks with wireless information and power transfer[J]. IEEE Transactions on Communications, 2019, 67(8): 5659-5673. DOI:10.1109/TCOMM.2019.2910260 |
| [10] |
鲍慧, 李梦辉, 赵伟. 认知MIMO中基于全双工的自我干扰回收研究[J]. 华中科技大学学报(自然科学版), 2019, 47(2): 36-40. |
| [11] |
ZHENG L F, LIU D, WEN Z G, et al. Robust beamforming for multi-user MISO full-duplex SWIPT system under non-linear energy harvesting model[J]. IEEE Access, 2021, 9: 14387-14397. |
| [12] |
XU Z G, LV Y, LIU J X, et al. Joint offloading and beamforming design in full-duplex multi-hop SWIPT MEC systems under non-linear energy harvesting model[J]. IET Communications, 2022, 16(18): 2171-2182. |
| [13] |
LIU D, ZHONG L, XU Z G, et al. Beamforming design for MIMO full-duplex SWIPT IoT system under imperfect CSI[J]. IET Communications, 2021, 15(14): 1849-1858. |
| [14] |
LU Y, XIONG K, FAN P Y, et al. Worst-case energy efficiency in secure SWIPT networks with rate-splitting ID and power-splitting EH receivers[J]. IEEE Transactions on Wireless Communications, 2022, 21(3): 1870-1885. |
| [15] |
LI M, LI N, WU H, et al. On the maximization of secrecy energy efficiency in full-duplex bidirectional system with SWIPT [C]//2019 IEEE wireless communications and networking conference (WCNC). Piscataway, NJ, USA: IEEE, 2019: 1-6.
|
| [16] |
CHEN P, LI T, FANG X. Secure beamforming and artificial noise design in full-duplex wireless-powered relay networks [C]//2019 IEEE 11th international conference on communication software and networks (ICCSN). Piscataway, NJ, USA: IEEE, 2019: 789-794.
|
| [17] |
LI M, TAO X, LI N, et al. Multi-objective optimization for full-duplex SWIPT systems[J]. IEEE Access, 2020, 8: 30838-30853. |
| [18] |
雷维嘉, 周洋. MIMO全双工双向通信系统平均保密率和速率的优化[J]. 电子学报, 2020, 48(6): 1041-1051. |
| [19] |
丁青锋, 奚韬, 连义翀, 等. 基于物理层安全的空间调制系统天线选择算法[J]. 计算机科学, 2020, 47(7): 322-327. |
| [20] |
杨广宇, 仇洪冰. 保密多输入多输出无线携能系统的节能稳健优化[J]. 上海交通大学学报, 2020, 54(4): 369-375. |
| [21] |
LI B, FEI Z S, CHU Z. Optimal transmit beamforming for secure SWIPT in a two-tier HetNet[J]. IEEE Communications Letters, 2017, 21(11): 2476-2479. |
| [22] |
LI B, FEI Z S, CHU Z, et al. Secure transmission for heterogeneous cellular networks with wireless information and power transfer[J]. IEEE Systems Journal, 2018, 12(4): 3755-3766. |
| [23] |
ZHANG B, HUANG K Z, JIN L, et al. Robust secrecy energy efficiency optimisation in heterogeneous networks with simultaneous wireless information and power transfer: centralised and distributed design[J]. IET Communications, 2019, 13(17): 2857-2870. |
| [24] |
朱政宇, 徐金雷, 孙钢灿, 等. 基于IRS辅助的SWIPT物联网系统安全波束成形设计[J]. 通信学报, 2021, 42(4): 185-193. |
| [25] |
ZHU Z Y, XU J L, SUN G C, et al. Robust beamforming design for IRS-aided secure SWIPT terahertz systems with non-linear EH model[J]. IEEE Wireless Communications Letters, 2022, 11(4): 746-750. |
| [26] |
FERNANDEZ S, LOPEZ-MARTINEZ F J, GREGO-RIO F H, et al. Secure full-duplex wireless power transfer systems with energy-information correlation[J]. IEEE Access, 2022, 10: 16952-16968. |
| [27] |
肖楠, 李陶深, 王哲. 带有下行SWIPT的强干扰WP-CN中用户最小速率最大化的研究[J]. 广西科学, 2019, 26(3): 267-275. DOI:10.13656/j.cnki.gxkx.20190618.007 |
| [28] |
ZHENG G, KRIKIDIS I, LI J, et al. Improving physical layer secrecy using full-duplex jamming receivers[J]. IEEE Transactions on Signal Processing, 2013, 61(20): 4962-4974. |
| [29] |
张颖. 面向全双工物理层安全的预编码技术研究[D]. 成都: 电子科技大学, 2017.
|
| [30] |
朱晴, 李陶深, 王哲, 等. 能效优先的全双工异构携能通信网络资源分配[J]. 小型微型计算机系统, 2023, 44(1): 177-184. |



