【研究意义】股票市场具有很高的风险,若股票价格波动太大或稳定性太低,它的风险会变得不可控。全球大多数股票都具有惯性效应,它是价格趋势的一种特殊情况。这些金融资产收益率在短期 (1年以内) 内具有持续性,而从长期 (1年以上) 看会出现反转[1]。从Jegadeesh[2]后,许多研究者开始从不同的方面对金融资产的可预测性进行探索。【前人研究进展】Hong等[3]试图用一种统一的理论解释股票市场中的过度反应、动量交易以及反应不足的情况。Asness等[4]指出:股票、外汇、大宗商品、股指期货、股指以及债券中均存在趋势。姜富伟等[5]研究了中国股票市场中样本内和样本外的可预测性。韩豫峰等[6]通过研究中国股市的股票特征来判定惯性与特征的相关性, 发现惯性与这些特征极为相关,指出中国股票市场与其他国家股票市场都存在趋势。但该文并没有对如何预测中国股票市场的趋势 (或短期惯性) 进行研究。【本研究切入点】通过构建若干技术指标,改进优化指数平滑异同移动平均线 (MACD) 模型,融合运用线性回归和机器学习方法,对中国股票市场价格变化趋势进行预测。【拟解决的关键问题】基于MACD模型,引入新增交易活跃程度 (ACT)、波动率 (VOL) 和离差值 (DIF) 趋势程度3个指标来控制产生股票交易的信号,并利用机器学习方法对显著影响惯性效应的特征 (股票特征、股票投资者的类型、宏观经济政策) 进行筛选,再对MACD策略中产生的买卖点进行改进优化,以使其收益更高且 (或) 风险更低,提出一种股票价格趋势预测方法。
1 优化的MACD模型 1.1 数据预处理为了使股票的波动趋势更具多样性,设计的交易策略更具有普遍性,挑选43个行业 (电力、房地产、钢铁、港口业、化工、酿酒、有色金属、银行等) 共93种股票,2005年1月到2016年1月的分钟级数据。所有数据均为上海证券交易所和深圳证券交易所的上市股票,且从Wind资讯平台下载 (该平台发布信息和数据准确率达到99.95%)。
由于某些股票分钟级市场活跃度低、交易频率被限制,所以将提取的93只分钟级样本数据处理成日线级别,即基于日线来设计交易策略。获取数据后,将数据整理成标准输入矩阵,前期还需要将股票按照全时间序列排列,并对数据进行补洞处理。
1.2 优化MACD指标通过Excel的VBA编程对MACD指标优化并建模。MACD指标由离差值 (DIF)、异同平均数 (DEA)、MACD柱状图,两线一柱3部分组成。EMAMt和EMANt分别为第t天的M日指数移动平均以及N日指数移动平均,其中M>N。
| $ \begin{array}{l} {\rm{EM}}{{\rm{A}}_{Nt}} = {\rm{EM}}{{\rm{A}}_{Nt - 1}}\left( {N - 1} \right)/\left( {N + 1} \right) + 2{C_t}/\\ \left( {N + 1} \right), \end{array} $ | (1) |
| $ \begin{array}{l} {\rm{EM}}{{\rm{A}}_{Mt}} = {\rm{EM}}{{\rm{A}}_{Mt - 1}}\left( {M - 1} \right)/\left( {M + 1} \right) + 2{C_t}/\\ \left( {M + 1} \right), \end{array} $ | (2) |
| $ DI{F_t} = {\rm{EM}}{{\rm{A}}_{Nt}} - {\rm{EM}}{{\rm{A}}_{Mt}}, $ | (3) |
| $ \begin{array}{l} {\rm{DE}}{{\rm{A}}_{Pt}} = {\rm{DE}}{{\rm{A}}_{Pt - 1}}\left( {P - 1} \right)/\left( {P + 1} \right) + 2{\rm{DI}}{{\rm{F}}_t}/\\ \left( {P + 1} \right), \end{array} $ | (4) |
| $ {\rm{MAC}}{{\rm{D}}_t} = 2\left( {{\rm{DI}}{{\rm{F}}_t} - {\rm{DE}}{{\rm{A}}_{Pt}}} \right)。$ | (5) |
当短周期的EMA穿过较长周期的EMA时,会出现交叉信号。交叉信号的方向由移动平均交叉的方向决定。当较短周期的EMA线向上穿越较长周期的EMA线时,会产生积极交易信号,即买入信号,意味着出现逐渐上升的积极时机;当较短周期的EMA线向下穿越较长周期的EMA线时,会产生消极信号,即卖出信号,意味着出现逐渐上升的消极时机。
基于MACD指标的股票价格趋势预测策略中,涉及到两种收盘价格,一种用于产生交易信号的收盘价格,另一种作为计算股票交易累积收益时的收盘价格。原因在于加载策略到买入股票的过程中,会产生时间差,导致产生交易信号的价格与最终交易买入股票的价格有差别。本研究采用两种收盘价格来建立交易模型,使MACD策略算出的累积收益更加接近真实交易时的收益。
由于MACD是一种具有明显趋势的策略,当行情为趋势型时有很好的效果,但当行情为震荡型时会产生很多假信号。因此引入股票市场活跃程度 (ACT)、波动率 (VOL)、DIF趋势程度 (K) 指标来辅助MACD指标,使产生更加稳健的交易信号。又由于交易者比较倾向于活跃度高的市场,故取某一时刻的数据来计算市场活跃度具有突发性和偶然性,并不能代表这段时间市场的具体情况。设HMt和LNt分别为第t天股票价格最高价的M日指数移动平均,第t天股票价格最低价的N日指数移动平均,StdCPt为第t天收盘价标准差的P日指数移动平均:
| $ {\rm{ACT = }}\left( {{H_{Mt}} - {L_{Nt}}} \right)/{\rm{Std}}{{\rm{C}}_{Pt}}。$ | (6) |
若股票的活跃性比较大,波动性也会变大。此时若缺少风险管理工具,就会存在较大的风险,使市场失去吸引力。股票价格的波动越剧烈,波动率就越高,资产收益率的不确定性就越强。本研究主要研究历史波动率,即根据时间序列来分析处理历史数据,并用22 d收盘价移动平均除以当天的收盘价来计算历史波动率。CQ t为第t天股票价格收盘价的Q日指数移动平均:
| $ VOL = {C_{Qt}}/{C_t}。$ | (7) |
DIF是快均线减去慢均线的差,当股票价格的整体趋势趋于平稳,但波动比较大时,快均线和慢均线会出现短时间内反复交叉的情况。当行情震荡波动严重时,会产生大量的假信号导致交易成本急剧上升。为此,增加一个DIF趋势程度指标,用于度量DIF的斜率,当斜率比较大时,即其当与0轴所围成的夹角比较大时,认为此时产生的交易信号是可信的。使用22 d收盘价的斜率除以当天的收盘价来计算DIF趋势程度。SRt为第t天股票价格收盘价的R日指数移动平均的斜率:
| $ K = {S_{Rt}}/{C_t}。$ | (8) |
对交易策略的参数以及股票进行挑选,并对挑选出来的股票所产生的交易信号以及收益进行记录。由于并非每一个交易信号产生的收益均为正,所以通过采取机器学习方式对产生的交易信号进行预测。若预测的收益为负,且MACD策略产生的收益为负,则去除该交易点。
2.1 参数选择交易之前剔除风险大于回报的股票,缩小选择股票的范围。基于统计分析方法,采用VBA编程对Excel数据表中股票进行筛选。
MACD策略有3个参数,分别为Long,Middle和Short。为了得到最佳的收益,对于不同特征的股票数据,这3个参数值的选择也不尽相同。比如MACD (5, 35, 5) 比MACD (12, 26, 9) 具有更高的敏感性,更加适合于周线。3个参数的变化范围见表 1。又使用变量Pnl来表示累积收益,其中累计收益Pnl是关于Long、Middle、Short的函数,记为Pnl (Long, Middle, Short)。
| 表 1 (L, M, S) 变化范围 Table 1 Range of (L, M, S) value |
对于每一种股票,都需要加载MACD策略,并用三重循环实现参数 (Long, Middle, Short) 的变化,每一组参数都对应一个Pnl (Long, Middle, Short) 值,最终算出该只股票所有的Pnl值。采用热点图方式选出最好的Pnl值,并记录下它所对应的 (Long, Middle, Short) 的值。为方便表示热点图,需要固定1个点,将3维变成2维。选择了5个Middle的值和5个Short的值,如表 2所示。
| 表 2 Short和Middle参数值 Table 2 Values of short and middle |
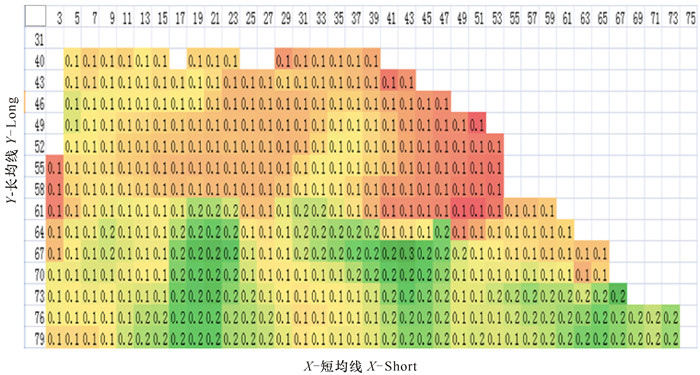
图 1中的每个小方格均代表一个Pnl (Long, Middle, Short) 值。参数Middle固定为42, Short、Large的值在规定的范围内变动,从图 1中筛选出3对 (Long, Short) 的值。同理固定参数Short,从对应的热点图中选出3对 (Long, Middle)。热点图的颜色变化表示收益变化,绿色表示累积收益较高,即Pnl (Long, Middle, Short) 较大的参数对,红色表示累积收益较低,即Pnl (Long, Middle, Short) 较小的参数对。分别固定选出的5个Short的值,在参数变化范围内变动 (Long, Middle) 的值。同理,分别固定选出的5个Middle的值,在参数变化范围内变动 (Long, Short) 的值。最终做出10个热点图,从每个热点图中选出3对 (Long, Middle) 以及3对 (Long, Middle),最终选出30对 (Long, Middle, Short) 值,见表 3。
|
图 1 热点图示例 Fig.1 Example of heap map |
| 表 3 选择的参数值 Table 3 Selected parameter values |
从93种股票数据的前100个Pnl (L, M, S) 中,找到与表 3中 (L, M, S) 匹配的参数值所对应的年化收益率,即Pnl值,并计算它们的最大值 (Max)、最小值 (Min)、平均值 (Avg)。对应计算出的最大值、最小值、平均值排序就可以从93只股票集中挑选出相对表现好的股票或者适应性较好的股票,如表 4所示。
| 表 4 挑选的股票代码 Table 4 Selected stocks ID |
在R语言中可以直接通过lm () 函数探究自变量 (特征变量)X与因变量 (累积收益)Y之间的线性关系。本文的研究中包含71个自变量X。采用多元回归方法分析他们之间的关系。图 2给出了线性回归预测的因变量值Y1和真实值Y之间的关系。横轴表示预测的收益值Y1、纵轴表示MACD模型产生的收益Y。若Y1与Y的值完全相同,那么画出的图形就应该是一条离散的直线。从图 2可以判断,若MACD模型产生的收益Y为负值,且预测的收益值Y1也为负值,那么该交易信号将被取消,即以0点为中心点的第三象限的交易信号将被全部取消。

|
图 2 线性回归预测 Fig.2 Linear regression prediction |
支持向量机 (SVM) 是一个有监督作用的学习模型,它既可以分析线性情况,也可以对线性不可分的情况进行分析,可以获得二值输出。相关向量机 (RVM) 是一种与SVM类似的监督学习方法。RVM与SVM的区别:RVM在贝叶斯框架下进行训练,它可以获得二值输出以及概率输出。
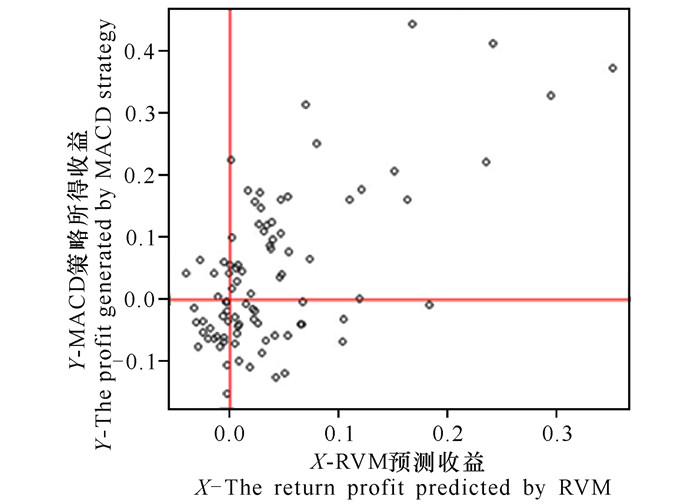
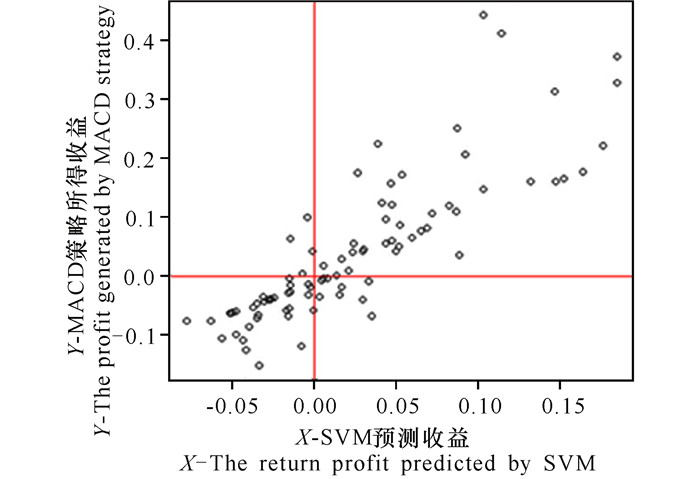
由于影响股票数据的因素之间大多存在非线性关系, 为此,采用RVM和SVM方法寻找出累积收益与特征变量之间的非线性关系。图 3和图 4分别给出使用RVM和SVM对因变量Y进行预测的结果。
|
图 3 利用RVM预测的结果 Fig.3 Prediction results by RVM |
|
图 4 利用SVM预测的结果 Fig.4 Prediction results by SVM |
由图 3和图 4可以看出,SVM比RVM的预测能力更强,其中SVM的点可以用一元一次函数拟合,预测的Y1值比较接近真实的Y值。同理,从图 3、图 4中可以判断,若MACD模型产生的收益Y为负值,且通过SVM或者RVM预测的收益值Y1也为负值,那么该交易信号将被取消,即以0点为中心点的第三象限的交易信号将被全部取消。
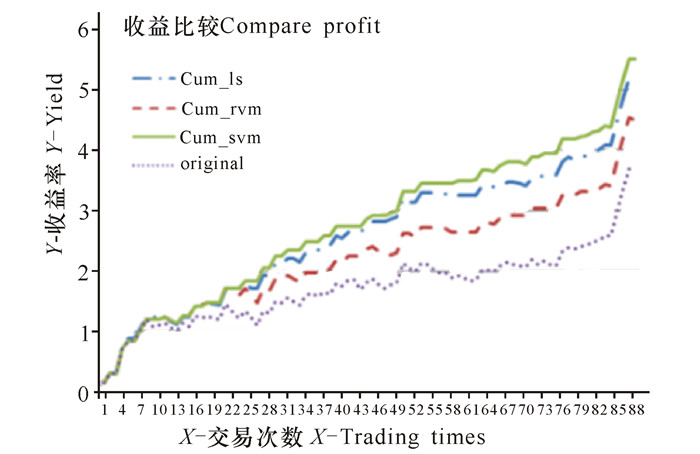
3 验证分析机器学习训练模型的整个过程,通过R语言在R-Studio平台上实现。用线性回归、SVM或者RVM对交易信号进行改进。若MACD模型产生的收益Y为负值,且通过线性回归、SVM或者RVM预测的收益值Y1也分别为负值,那么通过线性回归、SVM或者RVM进行预测后为负的交易信号将被取消,即以0点为中心点的第三象限的交易信号将被全部取消。最后将线性回归、RVM、SVM各自对MACD策略的交易信号进行优化后得到的累积收益与MACD策略的累积收益进行比较。收益比较结果见图 5。
|
图 5 累积收益比较 Fig.5 Comparison for market accumulated earning |
图 5中曲线Cum_ls表示采用线性回归方法对MACD策略交易产生的交易信号进行改进后得到的累积收益, Cum_rvm表示采用RVM对MACD策略交易产生的交易信号进行改进后得到的累积收益, Cum_svm表示采用SVM对MACD策略交易产生的交易信号进行改进后得到的累积收益, original表示采用MACD策略交易产生的交易信号的累积收益。从图 5可看出,使用机器学习方法对MACD策略进行改进后的收益均比原模型有一定的改善;另一方面,采用线性回归、RVM方法改进的效果相对较小,而采用SVM方法改进的效果较大。
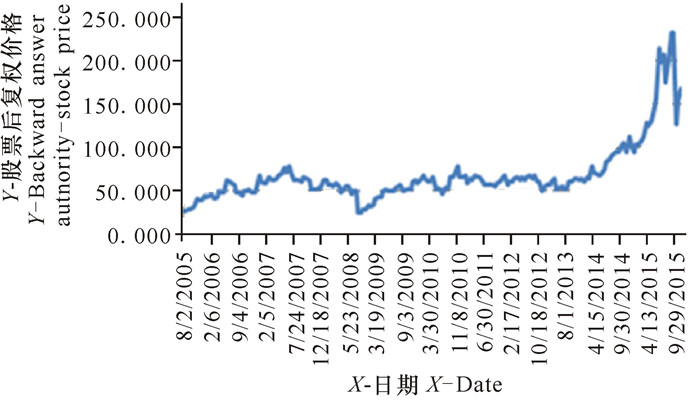
图 6给出了代码为002025股票价格的曲线。将图 5累积收益与图 6的股票价格在时间上进行对比,可以看出:当股票价格呈上升趋势时,收益增幅较大。例如, 2015年7月到2016年9月股票价格持续上涨明显,收益也大幅增加。说明改进的交易策略能够有效避开价格震荡区域, 如2007年2月到2007年12月的区域;在区间2008年5月到2008年8月股票价格下跌时,采用SVM改进模型获得的交易信号能够有效的避免下跌风险。
|
图 6 股票价格 Fig.6 Stock Price |
虽然股票市场是一个复杂的非线性动态系统,但可以通过抓住股票市场的趋势来提高股票投资的准确性。本文通过加入3个指标来控制产生的交易信号,改进了交易策略,通过画出累积收益的热点图对参数Long、Middle和Short以及股票进行选择;运用线性回归、RVM、SVM方法对MACD策略的交易信号进行优化,从而使交易模型预测获得的收益更高且 (或) 风险更低。当数据中噪音数量过多时,SVM的方差会受噪音的影响而变大,结果也会受到影响,这是后续工作需要研究解决的问题。此外,本文给出的交易策略是基于历史数据建模,下一步将研究通过不断更新数据和训练模型,以获得更好的预测效果。
| [1] |
MOSKOWITZ T J, OOI Y H, PEDERSEN L H. Time series momentum[J]. Journal of Financial Economics, 2012, 104(2): 228-250. DOI:10.1016/j.jfineco.2011.11.003 |
| [2] |
JEGADEESH N. Evidence of predictable behavior of security returns[J]. The Journal of Finance, 1990, 45(3): 881-898. DOI:10.1111/j.1540-6261.1990.tb05110.x |
| [3] |
HONG H, STEIN J C. A unified theory of underreaction, momentum trading, and overreaction in asset markets[J]. The Journal of Finance, 1999, 54(6): 2143-2184. DOI:10.1111/0022-1082.00184 |
| [4] |
ASNESS C S, MOSKOWITZ T J, PEDERSEN L H. Value and momentum everywhere[J]. The Journal of Finance, 2013, 68(3): 929-985. DOI:10.1111/jofi.12021 |
| [5] |
姜富伟, RAPACH D E, STRAUSS J K, 等. 中国股票市场可预测性的实证研究[J]. 金融研究, 2011(9): 107-121. JIANG F W, RAPACH D E, STRAUSS J K, et al. How predictable is the Chinese stock market?[J]. Journal of Financial Research, 2011(9): 107-121. |
| [6] |
韩豫峰, 汪雄剑, 周国富, 等. 中国股票市场是否存在趋势?[J]. 金融研究, 2014(3): 152-163. HAN Y F, WANG X J, ZHOU G F, et al. Are there trends in Chinese stock market?[J]. Journal of Financial Research, 2014(3): 152-163. |
 2017, Vol. 33
2017, Vol. 33 

