脑电图(Electroencephalogram,EEG)通过记录神经元的电活动反映大脑的功能状态,是一种常用的非侵入性技术,广泛应用于临床诊断、认知科学研究和脑机接口(Brain-Computer Interface,BCI)等领域[1-3]。EEG数据包含丰富的脑功能信息,但其复杂的时空动态性、高噪声和个体差异性等特点,给EEG数据处理任务如特征提取、模式分类带来了巨大挑战。传统的时频分析和独立成分分析(Independent Component Analysis,ICA)等方法,虽然能够在一定程度上处理EEG数据,但是由于无法全面捕捉EEG数据中的复杂模式,导致模型性能受限。因此,如何更高效地处理和解读EEG数据,已成为推动脑科学研究和应用发展的关键问题。
近年来,深度学习模型为EEG数据分类提供了新的研究方向。例如,改进的卷积神经网络(Convolutional Neural Network,CNN)模型ConvNet[4]和EEGNet[5]在EEG数据分类任务上表现出了出色的性能,能够通过卷积操作有效地提取EEG数据中的局部特征。然而,由于CNN的局部接受域限制,CNN难以捕捉EEG数据中的长期时序依赖关系。为解决这一问题,递归神经网络(Recurrent Neural Network,RNN)和长短期记忆网络(Long Short-Term Memory,LSTM)被研究者提出,用于捕获EEG数据的时序特征[6-8]。尽管如此,这些方法在处理长数据序列时仍存在梯度消失问题,限制了其在EEG数据分类中的应用。为克服这一问题,Transformer被引入EEG数据分类任务中,其强大的并行计算能力可有效解决梯度消失问题,能够更好地从EEG数据中提取信息。基于Transformer的Conformer[9]和EEG-deformer[10]等模型均结合了CNN和Transformer的优势,充分利用CNN在局部特征提取上和Transformer在全局特征建模上的长处,显著增强了模型对EEG数据的全局理解,比传统方法的性能更好。然而,上述模型所使用的Transformer采用静态位置编码,静态位置编码由于其固定性,无法适应EEG数据中不断变化的动态特性,导致其对EEG数据全局时序依赖关系的建模不准确,尤其是在处理高噪声或非平稳信号时,Transformer在EEG数据分类任务中的准确性和鲁棒性会显著下降。
为解决静态位置编码限制Transformer在EEG数据分类任务中应用的问题,本研究提出用残差循环神经网络(Residual Recurrent Neural Network,ResRNN)的输出作为动态位置编码的CRRT模型,其功能如图 1所示。具体来讲,该模型将CNN、ResRNN和Transformer相结合:CNN用于提取EEG数据的局部空间特征,ResRNN用于捕捉EEG数据的时序依赖特性,Transformer用于捕获EEG数据的全局特征。残差连接使得ResRNN能够有效解决梯度消失问题,从而避免了传统RNN在长数据序列处理中常见的梯度消失问题。同时,ResRNN的输出被用作动态位置编码,动态位置编码能够根据输入信号的实时特性调整位置信息,从而更好地适应EEG数据复杂的时空动态变化,为Transformer提供了更灵活的时间序列位置表示。这种灵活性使得Transformer能够更加精确地应对EEG数据中的时空动态性、高噪声和个体差异性问题,从而有效提升对EEG数据全局特征的捕获能力,进一步强化Transformer在EEG数据分类中的建模能力和鲁棒性。但是,ResRNN和Transformer同时使用会导致模型参数量过大,为此,本研究设计了ResRNN-Transformer模块与模块之间的参数共享,这样不仅可以解决ResRNN和Transformer一起使用导致的参数量过大的问题,而且还可以简化模型结构,解决过拟合问题。
|
| 图 1 CRRT功能 Fig.1 CRRT function |
1 相关工作 1.1 使用单一深度学习模型进行EEG数据分类
随着机器学习技术的进步,EEG数据分类研究得到了显著发展[11-13]。Sakhavi等[14]利用CNN从滤波器组Common Spatial Pattern (CSP)特征中提取时间信息,并为每个受试者定制网络架构。Shan等[15]通过引入图结构捕捉EEG数据的跨通道拓扑连接,构建了更具表现力的时空卷积网络。此外,Hong等[16]提出一种基于对抗学习的自适应框架,并应用CNN提取了不依赖于个体差异的通用特征。Huang等[17]和Roy[18]还提出了一些增强CNN性能的策略,特别是在运动想象任务的EEG数据分类中,这些策略显著提升了分类的精度和鲁棒性。
1.2 使用混合模型进行EEG数据分类近年来,EEG数据处理领域涌现了多种结合不同神经网络架构的混合模型。CNN-LSTM[8]结合了CNN和LSTM的优势,分别处理EEG数据中的空间特征和时间依赖性。Pham等[19]通过CNN提取空间特征,并使用LSTM捕捉EEG数据的时序依赖性,专注于睡眠阶段分类,结果显示LSTM能够有效地捕捉时间序列中的长期依赖关系。Song等[9]、She等[10]将CNN和Transformer两者结合应用于EEG数据处理上,提高了EEG数据分类的准确性。
2 方法 2.1 方法概述如图 2所示,CRRT模型的核心思路是用CNN提取EEG数据的局部空间特征,而ResRNN-Transformer模块负责捕捉EEG数据的时序依赖性及全局特征。ResRNN不仅可以提取时序信息,而且还可以为Transformer提供动态位置编码,从而增强模型的适应性。ResRNN-Transformer模块中的N个块之间的参数是共享的,从而减少模型参数量。
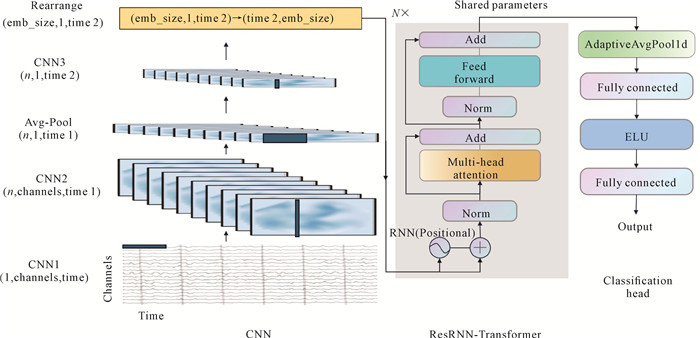
|
| 图 2 CRRT模型总体框架结构 Fig.2 Overall framework of CRRT model |
2.2 数据预处理
原始EEG数据的形状为(channels,time)(channels为电极通道数,time为时间长度),具有高噪声、非平稳性和复杂的时间依赖性。因此,在应用深度学习模型之前,进行有效的数据预处理是至关重要的一步。本研究的预处理步骤包括以下两个方面。
滤波:使用带通滤波器去除EEG数据中的高频和低频噪声。设置4-40 Hz的滤波范围,保留与脑电活动相关的主要频段信息,提升数据的信噪比。
Z-score标准化:对每个通道的数据进行标准化,以减少因信号幅度差异造成的影响。具体采用Z-score标准化,其公式为
| $ x_{\mathrm{norm}}=\frac{x-\mu}{\sigma}, $ | (1) |
其中,xnorm是标准化后的信号,x是输入信号,μ为均值,σ为标准差。通过该标准化方法,所有通道的数据将具有相同的尺度,从而提升模型的稳定性和分类性能。
上述预处理步骤有助于减少EEG数据中的噪声干扰,并确保不同通道的信号在同一尺度上进行处理,为后续的深度学习模型提供更干净、更具一致性的数据输入。
2.3 网络架构如图 2所示,本研究所提出的模型由3个主要模块构成:卷积模块(CNN)、ResRNN-Transformer模块和分类头模块(Classification head)。每个模块在EEG数据处理过程中发挥独特的作用,协同工作以提取时空特征并实现最终的分类任务。
2.3.1 卷积模块卷积模块的目的是高效提取EEG数据的时间和空间特征,并通过多层卷积融合不同电极通道的特征。为方便后续的卷积操作,首先对数据拓展一个维度,由原来的(channels, time)变成(1, channels, time)。受Conformer[9]的启发,卷积设计如图 2左边CNN区域所示。CNN模块构建主要有以下步骤。
第一步,通过第一层卷积沿时间维度提取特征,采用的卷积核大小为(1,k),不使用激活函数和归一化操作,保留足够的时间细节,以便将线性组合后的特征图传递至下一层。此层卷积捕捉EEG数据的局部时间特征。
第二步,通过第二层卷积沿空间维度(电极通道)进行卷积,卷积核大小为(channels,1)。该层卷积进一步优化时间特征和空间特征。
第三步,通过平均池化层降低时间维度,平滑时间特征,并抑制噪声干扰,提高模型的泛化能力。
第四步,使用卷积核为(1,1)的第三层卷积对空间特征进行升维,将多个电极通道的空间特征融合成一个高维表示,供后续模块进一步处理。
卷积模块的详细超参数如表 1所示(基于BCI Competition Ⅳ Dataset 2a[20]的卷积超参数)。CNN3的输出经过重新排列(Rearrange)后,将每个时间点的所有通道特征整合为一个标记序列(Token),以输入ResRNN-Transformer模块。这种设计确保了局部特征的有效学习,并增强了时间和空间特征的表达能力,为后续模块提供优质输入。
| 层 Layer |
输入 Input |
卷积核 Kernel |
步长 Stride |
输出 Output |
| CNN1 | 1, 22, 1000 | (1, 25) | (1, 1) | 1, 22, 976 |
| CNN2 | 1, 22, 976 | (22, 1) | (1, 1) | 40, 1, 976 |
| Ave-Pool | 40, 1, 976 | (1, 75) | (1, 15) | 40, 1, 61 |
| CNN3 | 40, 1, 61 | (1, 1) | (1, 1) | emb_size, 1, 61 |
| Rearrange | emb_size, 1, 61 | 61, emb_size |
2.3.2 ResRNN-Transformer模块
在卷积模块提取局部特征的基础上,ResRNN-Transformer模块负责捕捉EEG数据中的时序依赖性和全局特征。如图 3所示,ResRNN在每个时刻的输出不仅包含当前输入信息,而且还隐含了前面所有时刻输入的信息,从而能够动态捕获时序依赖关系。这种特性使其适合为Transformer提供动态位置编码,从而增强Transformer对序列信号变化的适应能力。为进一步简化模型结构并降低参数量,本研究仅提取ResRNN隐藏层h的输出作为动态编码部分,在保证时序建模效果的同时,减少模型的复杂性。
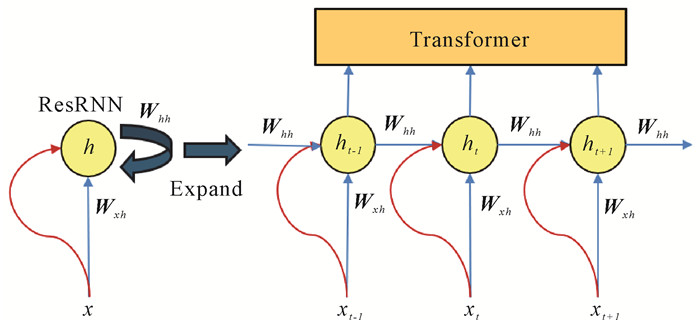
|
| 图 3 ResRNN-Transformer流程 Fig.3 ResRNN-Transformer process |
RNN隐藏层h的公式如下:
| $ h_t=f\left(\boldsymbol{W}_{x h} x_t+\boldsymbol{W}_{h h} h_{t-1}+b_h\right), $ | (2) |
| $ \tanh (x)=\frac{e^x-x^{-x}}{e^x+e^{-x}}, $ | (3) |
其中,ht为第t个时刻的层隐藏状态,ht-1是上一时刻的层隐藏状态,x为输入,xt为第t时刻的输入,Wxh是输入x到隐藏层h间的权重矩阵,Whh是隐藏层ht-1到隐藏层h间的权重矩阵,bh是偏置项,f是tanh激活函数。
为防止RNN在捕捉时序信息时丢失原始特征,在RNN层中引入残差连接,即ResRNN,通过将输入直接与输出相加,增强模型对原始信号的保留能力,同时提升特征表达的丰富性。其公式为
| $ \operatorname{ResRNN}(x)=x_t+h_t, $ | (4) |
这种连接方式可以保留更多的原始信号信息。残差连接的引入确保模型在捕捉时序信息的同时保留xt原有的特征。
如图 3所示,在ResRNN处理的基础上,Transformer进一步通过其自注意力机制整合EEG数据的全局信息。具体流程如图 2所示,Transformer利用多头自注意力机制捕捉EEG数据中的复杂依赖关系,从而使模型能够深度理解信号的全局结构和动态变化特性。自注意力(Self-Attention)具体公式为
| $ \text { Self - Attention }(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{softmax}\left(\frac{\boldsymbol{Q K} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_k}}\right) \boldsymbol{V}, $ | (5) |
其中,Q、K、V分别是查询(Query)、键(Key)、值(Value)矩阵,dk是键矩阵的维度,用于缩放内积结果,避免因向量维度过大导致的梯度不稳定。多头自注意力将输入矩阵分成多个子空间,每个子空间独立进行注意力计算,并捕捉输入信号的不同特征模式。其输出特征通过拼接(Concat)操作后再传递到后续的前馈神经网络(Feedforward Network, FFN)进行处理,前馈神经网络公式如下:
| $ X_{f f}=\operatorname{FFN}(x)=\operatorname{GELU}\left(x \boldsymbol{W}_1+b_1\right) \boldsymbol{W}_2+b_2, $ | (6) |
| $ \begin{aligned} & \mathrm{GELU} \approx 0.5 X\left(1+\tanh \left(\sqrt{\frac{2}{\pi}}(X+\right.\right. \\ & \left.\left.\left.0.044715 X^3\right)\right)\right), \end{aligned} $ | (7) |
其中,Xff是输出,FFN是一个两层的全连接网络,W1、W2是全连接层的权重矩阵,b1、b2是对应的偏置项,GELU是高斯误差线性单元激活函数,X是GELU激活函数的输入。
2.3.3 分类头模块ResRNN-Transformer模块中的输出会传递至分类头模块,用于完成最终的分类任务。分类头模块通过一维自适应平均池化(AdaptiveAvgPool1d)对特征的时间维度进行压缩,从而有效降低模型复杂度,同时保留关键信息。其公式如下:
| $ x_{\text {pool }}=\text { AdaptiveAvgPool1d }(x), $ | (8) |
其中,xpool是池化后的特征。这种池化操作的核心是通过对每个指定的池化区间内的元素取平均值来实现压缩,既能降低输入的时间维度,又可以避免丢失全局信息。自适应平均池化的优势在于输出的维度是固定的,这为后续全连接层的处理奠定了基础,同时又显著降低了模型复杂度。
池化后的特征随后传递至两层全连接层(Fully connected layers),使用ELU激活函数引入非线性特性。全连接层的计算公式如下:
| $ H_1=\operatorname{ELU}\left(\boldsymbol{W}_1 x_{\text {pool }}+b_1\right), $ | (9) |
| $ \operatorname{ELU}(x)=\left\{\begin{array}{l} x, x \geqslant 0 \\ \infty(\exp (x)-1), x <0 \end{array}, \right. $ | (10) |
| $ P=\operatorname{softmax}\left(\boldsymbol{W}_2 H_1+b_2\right), $ | (11) |
其中,H1是第一层全连接的输出,P是最终的类别概率分布,W1和W2分别是第一层和第二层全连接层的权重矩阵,ELU和softmax是激活函数,softmax将输出归一化为类别的概率分布。softmax激活函数的计算公式如下:
| $ P_i=\frac{\exp \left(z_i\right)}{\sum_{j=1}^n \exp \left(z_j\right)} \quad \text { for } i=1, 2, \cdots, n, $ | (12) |
其中,Pi是类别i的预测概率;zi是输出层对应类别i的得分;
这种分类头设计利用一维自适应平均池化降低了特征维度和模型复杂度,同时通过ELU激活函数的平滑特性增强了模型的非线性表达能力,再结合两层全连接层和softmax激活函数,使得分类器能够准确生成每个类别的概率分布,从而显著提升EEG数据分类的精度与鲁棒性。
3 实验与结果分析在4个公开的EEG数据集(包括常用的运动想象和情绪识别任务)上进行实验,以验证所提出的CRRT分类模型的有效性。同时,将CRRT模型与其他先进的方法进行对比,评估其在不同数据集上的性能表现。
3.1 数据集在以下4个广泛使用的EEG数据集上对CRRT模型进行测试:BCI Competition Ⅳ Dataset 2a[20]、BCI Competition Ⅳ Dataset 2b[21]、SEED[22]和DEAP[23]数据集。每个数据集使用不同的采集设备、模式、受试者数量和样本量,从而验证模型的通用性。
BCI Competition Ⅳ Dataset 2a: 该数据集包含9名受试者的EEG数据,涉及4个运动想象任务——左手、右手、双脚和舌头的运动。EEG数据通过22个Ag/AgCl电极以250 Hz采样率采集,使用2-6 s时间段数据,并通过带通滤波器(4-40 Hz)处理。共进行2次实验,第1次实验用于训练,第2次实验用于测试,每次实验288条数据(每个任务72条)。
BCI Competition Ⅳ Dataset 2b:该数据集包含9名受试者的EEG数据,涉及左手和右手的运动想象任务。EEG数据通过3个双极电极(C3、CZ、C4)以250 Hz采样率采集,使用3-7 s时间段数据,并通过带通滤波器(4-40 Hz)处理。共有5次实验,每次120条数据,前3次实验用于训练,后2次实验用于测试。
SEED数据集:该数据集包含15名受试者的EEG数据,记录了受试者观看电影片段时的情绪反应(积极、中性、消极)。EEG数据通过62个电极以1 000 Hz采样率采集,并降采样至200 Hz。每个样本被分割为400长度的时间窗口,并经过带通滤波器(4-47 Hz)处理。
DEAP数据集:该数据集包含32名受试者的EEG数据,受试者根据情绪反应对视频进行评分。EEG数据采用512 Hz采样率,并降采样至128 Hz。每个样本被分割为384长度的时间窗口,并通过带通滤波器(4-47 Hz)处理数据。
3.2 数据增强EEG数据采集耗时较长,且由于实验设计限制、数据预处理及标注成本等因素,导致最终形成的有效数据集规模较小,容易出现过拟合问题。部分研究通过数据扩充来为模型提供更多样本。然而,传统的加高斯噪声或裁剪策略可能会降低信噪比或破坏原始信号的相干性。为此,对数据集BCI Competition Ⅳ Dataset 2a和BCI Competition Ⅳ Dataset 2b采用时域分割与重构方法生成新的数据。将同一类别的训练样本平均分为n个片段,并在保持原始时间顺序的基础上进行随机拼接[9]。在每一次迭代中,生成与批处理等量的增强数据。
3.3 实验设置和评价指标使用Adam优化器进行模型训练,初始学习率设为0.000 1,并通过学习率衰减策略逐步调整。在训练过程中,采用交叉熵损失函数优化模型参数。整个训练过程在NVIDIA 3090 GPU (24GB) 的计算环境中运行,借助PyTorch 12.1和Python 3.11以提升计算效率并加速模型收敛。分类精度与卡帕(Kappa)值被用作整体性能的评估指标,Kappa值的计算公式为
| $ \text { Карра }=\frac{p_{\mathrm{o}}-p_{\mathrm{e}}}{1-p_{\mathrm{e}}}, $ | (13) |
其中,po代表模型预测的准确率,pe为随机猜测的准确率。Kappa值的核心是比较模型预测的准确率和随机猜测的准确率之间的差异。如果Kappa值为1,说明模型的表现非常好,预测与实际完全一致;如果Kappa值为0,说明模型的表现与随机猜测一样,毫无意义。
3.4 基线比较在BCI Competition Ⅳ Dataset 2a的实验中(表 2,其中“S1”到“S9”表示9名受试者),CRRT模型表现出了卓越的性能,平均准确率达到81.09%,显著高于传统方法FBCSP(67.75%)及其他深度学习模型,如ConvNet(72.53%)和EEGNet(74.50%)。尤其在S1、S3、S7中,CRRT模型的准确率最高达94.79%,证明了其在处理复杂EEG数据时的优越能力和鲁棒性。与较新的模型如Conformer、M-FANet和Dual-TSST相比,CRRT模型的分类效果更好。CRRT模型的平均准确率高于Conformer(78.66%),提升了3.09%,并且Kappa值(0.745 3)也显著提高。CRRT模型通过引入动态位置编码,增强了对EEG数据时序信息的建模能力,提升了Transformer在时间序列处理方面的性能。与M-FANet和Dual-TSST相比,CRRT模型表现同样出色。M-FANet的平均准确率为79.28%(Kappa值0.725 9),Dual-TSST为79.55%(Kappa值0.741 3),但CRRT模型以81.09%的平均准确率领先,特别是在S7中的准确率(94.79%),显著高于M-FANet和Dual-TSST。
| 方法 Methods |
准确率/% Accuracy/% |
卡帕值 Kappa value |
|||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average | ||
| FBCSP[24] | 76.00 | 56.50 | 81.25 | 61.00 | 55.00 | 45.25 | 82.75 | 81.25 | 70.75 | 67.75 | 0.570 0 |
| ConvNet[4] | 76.39 | 55.21 | 89.24 | 74.65 | 56.94 | 54.17 | 92.71 | 77.08 | 76.39 | 72.53 | 0.633 7 |
| EEGNet[5] | 85.76 | 61.46 | 88.54 | 67.01 | 55.90 | 52.08 | 89.58 | 83.33 | 86.81 | 74.50 | 0.660 0 |
| C2CM[14] | 87.50 | 65.28 | 90.28 | 66.67 | 62.50 | 45.49 | 89.58 | 83.33 | 79.51 | 74.46 | 0.659 5 |
| FBCNet[25] | 85.42 | 60.42 | 90.63 | 76.39 | 74.31 | 53.82 | 84.38 | 79.51 | 80.90 | 76.20 | 0.682 7 |
| DRDA[26] | 83.19 | 55.14 | 87.43 | 75.28 | 62.29 | 57.15 | 86.18 | 83.61 | 82.00 | 74.70 | 0.663 2 |
| Conformer[9] | 88.19 | 61.46 | 93.40 | 78.13 | 52.08 | 65.28 | 92.36 | 88.19 | 88.89 | 78.66 | 0.715 5 |
| M-FANet[27] | 86.81 | 75.00 | 91.67 | 73.61 | 76.39 | 61.46 | 85.76 | 75.69 | 87.15 | 79.28 | 0.725 9 |
| Dual-TSST[28] | 91.32 | 59.38 | 93.40 | 69.44 | 77.79 | 68.75 | 94.44 | 85.76 | 75.69 | 79.55 | 0.741 3 |
| CRRT | 90.62 | 61.80 | 94.44 | 84.37 | 57.63 | 66.66 | 94.79 | 89.93 | 89.58 | 81.09 | 0.745 3 |
| Note:the best results of the comparative methods are highlighted in bold. | |||||||||||
在BCI Competition Ⅳ Dataset 2b的实验中(表 3,其中“S1”到“S9”表示9名受试者),CRRT模型表现优异,平均准确率达到87.66%,超过了实验的其他方法。与传统的FBCSP相比,CRRT模型在大部分受试者上的表现有显著提升,尤其在S7和S8中,准确率分别达到96.25%和98.43%。这表明CRRT模型能够有效应对EEG数据中的复杂性,并表现出卓越的分类能力和鲁棒性。与较新的方法相比,CRRT模型也展现出优势。虽然Conformer在准确率上表现优异(平均准确率为84.63%),但CRRT模型的平均准确率比其高出3.58%,而且CRRT模型的Kappa值(0.725 3)也超过了Conformer(0.692 6)。TSFCNet和EISATC-Fusion的平均准确率分别为84.17%和87.58%,但CRRT模型依然领先,尤其在S7和S8中,CRRT模型的表现更加突出。
| 方法 Methods |
准确率/% Accuracy/% |
卡帕值 Kappa value |
|||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average | ||
| FBCSP[24] | 70.00 | 60.36 | 60.94 | 97.50 | 93.12 | 80.63 | 78.13 | 92.50 | 86.88 | 80.00 | 0.600 0 |
| ConvNet[4] | 76.56 | 50.00 | 51.56 | 96.88 | 93.13 | 85.31 | 83.75 | 91.56 | 85.62 | 79.37 | 0.587 4 |
| EEGNet[5] | 75.94 | 57.64 | 58.43 | 98.13 | 81.25 | 88.75 | 84.06 | 93.44 | 89.69 | 80.81 | 0.609 6 |
| DRDA[26] | 81.37 | 62.86 | 63.63 | 95.94 | 93.56 | 88.19 | 85.00 | 95.25 | 90.00 | 83.98 | 0.679 6 |
| Conformer[9] | 82.50 | 65.71 | 63.75 | 98.44 | 86.56 | 90.31 | 87.81 | 94.38 | 92.19 | 84.63 | 0.692 6 |
| TSFCNet[29] | 76.25 | 70.00 | 83.75 | 97.50 | 72.81 | 86.56 | 88.44 | 92.50 | 89.69 | 84.17 | 0.723 4 |
| EISATC-Fusion[30] | 75.00 | 72.86 | 86.56 | 96.88 | 97.81 | 84.38 | 94.06 | 93.75 | 86.88 | 87.58 | |
| CRRT | 87.50 | 71.78 | 78.43 | 97.81 | 88.75 | 86.25 | 96.25 | 98.43 | 83.75 | 87.66 | 0.725 3 |
| Note:the best results of the comparative methods are highlighted in bold. | |||||||||||
在SEED数据集的实验中(表 4),CRRT模型表现出色,准确率达到97.31%,超越了所有的对比方法。与传统的SVM方法(准确率为86.08%,Kappa值为0.791 2)相比,CRRT模型在准确率和Kappa值上均有显著提升,表现出卓越的分类能力。与较新的方法相比,CRRT模型也展现了明显优势。尽管Conformer取得了95.30%的准确率(Kappa值为0.929 5),CRRT模型的准确率仍然高出其2.11%,并且Kappa值(0.957 4)也远高于Conformer。与Dual-TSST(准确率为96.65%,Kappa值为0.948 8)相比,CRRT模型同样具有优势,进一步证明了其在复杂情绪数据处理中的强大能力。
| 方法 Methods |
准确率/% Accuracy/% |
卡帕值 Kappa value |
| SVM[31] | 86.08 | 0.791 2 |
| GELM[32] | 91.07 | 0.866 1 |
| DGCNN[33] | 90.40 | 0.856 0 |
| R2G-STNN[34] | 93.38 | 0.900 7 |
| RGNN[35] | 94.24 | 0.913 6 |
| Conformer[9] | 95.30 | 0.929 5 |
| FTCN[36] | 89.16 | |
| Dual-TSST[28] | 96.65 | 0.948 8 |
| CRRT | 97.31 | 0.957 4 |
| Note:the best results of the comparative methods are highlighted in bold. | ||
在DEAP数据集上,CRRT模型同样表现出卓越的分类能力(表 5)。在效价(Valence)分类任务中,CRRT模型的准确率达到99.37%;在唤醒(Arousal)分类任务中,CRRT模型的准确率高达99.39%,超越所有对比方法。相比传统方法如SSTD(效价分类准确率为68.28%,唤醒分类准确率为71.48%)和MTLFuseNet(效价分类准确率为71.33%,唤醒分类准确率为73.28%),CRRT模型性能大为提升。此外,先进的深度学习模型如DSE-Mixer(效价分类准确率为95.19%,唤醒分类准确率为95.22%)、MT-CNN(效价分类准确率为96.28%,唤醒分类准确率为96.62%)和Caps-EEGNet(效价分类准确率为96.67%,唤醒分类准确率为96.75%)尽管表现出色,但是与CRRT模型相比仍有明显差距。即便是最新的MES-CTNet(效价分类准确率为98.31%,唤醒分类准确率为98.28%),在DEAP数据集上也未能达到CRRT模型的性能水平。CRRT模型通过对EEG数据中复杂的时空特征进行深入建模,表现出优异的泛化能力和全局特征提取能力,再次反映了其在情绪识别任务中的出色能力。
| 方法 Methods |
效价分类准确率/% Valence-accuracy/% |
唤醒分类准确率/% Arousal-accuracy/% |
| SSTD[37] | 68.28 | 71.48 |
| MTLFuseNet[38] | 71.33 | 73.28 |
| DSE-Mixer[39] | 95.19 | 95.22 |
| MT-CNN[40] | 96.28 | 96.62 |
| Caps-EEGNet[41] | 96.67 | 96.75 |
| MES-CTNet[42] | 98.31 | 98.28 |
| CRRT | 99.37 | 99.39 |
| Note:the best results of the comparative methods are highlighted in bold. | ||
3.5 鲁棒性实验
为评估CRRT模型在电极通道部分缺失情况下的鲁棒性,在包含22个电极通道的BCI Competition Ⅳ Dataset 2a上采取随机电极通道缺失策略,以模拟在采集EEG数据的实际过程中因环境干扰、设备故障或信号噪声等因素导致的电极信息丢失情况。具体实验中,分别设置随机剔除1、3、5、7、9以及11个电极通道的情形,并对各受试者(S1至S9)的EEG数据分类准确率进行比较,结果如表 6所示。虽然部分受试者的分类准确率出现了一定波动,但是整体平均分类准确率仅有轻微下降,仍维持在较高水平。这充分表明,即便在部分电极信息缺失的情况下,CRRT模型依旧表现出卓越的鲁棒性。
| 丢弃通道数 Number of discarded channels |
准确率/% Accuracy/% |
|||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average | |
| 0 | 90.62 | 61.80 | 94.44 | 84.37 | 57.63 | 66.66 | 94.79 | 89.93 | 89.58 | 81.09 |
| 1 | 91.31 | 61.80 | 93.05 | 81.25 | 59.05 | 63.54 | 93.75 | 88.19 | 88.54 | 80.05 |
| 3 | 90.62 | 60.76 | 93.05 | 78.81 | 57.63 | 65.62 | 91.66 | 88.54 | 88.19 | 79.43 |
| 5 | 91.31 | 64.23 | 92.36 | 81.94 | 56.25 | 62.84 | 90.97 | 88.54 | 89.93 | 79.82 |
| 7 | 89.93 | 62.15 | 91.66 | 78.12 | 58.68 | 62.84 | 88.54 | 87.50 | 90.97 | 78.93 |
| 9 | 88.54 | 63.19 | 91.31 | 79.51 | 59.72 | 63.54 | 84.72 | 86.80 | 88.88 | 78.47 |
| 11 | 88.19 | 62.84 | 89.23 | 78.81 | 56.59 | 61.45 | 84.02 | 87.84 | 87.50 | 77.39 |
3.6 消融实验 3.6.1 模块块数和共享参数对模型性能的影响
为研究ResRNN-Transformer模块块数和共享参数对模型性能的影响,比较在不同模块块数(0-8)下,模型参数共享与模型参数不共享时的模型表现。实验基于BCI Competition Ⅳ Dataset 2a,结果如图 4所示,可以看出参数共享的模型在模块块数增加至6时达到最高分类准确率(81.09%)。相比之下,参数不共享的模型在模块块数增加至6时其性能反而有所下降,准确率为79.05%。对于不共享参数的模型,尽管模块块数从1块增加到4块时准确率有所提升,但是在模块块数为4块及以上准确率出现了下降趋势,尤其是在模块块数为8块时降至78.97%。在共享参数的情况下,模型性能整体随模块块数增加而提升,但当模块块数超过6后,准确率有所回落(如7块的80.20%和8块的79.55%)。这表明适度增加模块的块数有助于提升模型的分类性能,尤其是在参数共享的情况下。然而,块数过多可能导致模型复杂性增加或过拟合,从而影响分类效果。这充分表明,共享参数策略在提高模型准确率和防止模型性能下降方面表现出一定的优势。
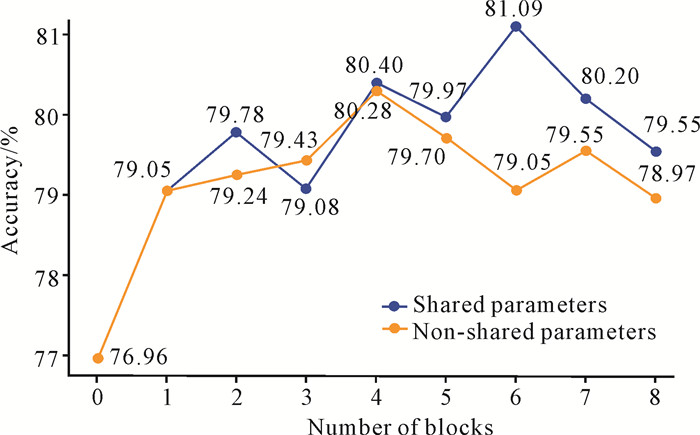
|
| 图 4 ResRNN-Transformer模块块数及模型参数是否共享对模型精度的影响 Fig.4 Impact of ResRNN-Transformer module blocks and whether the model parameters are shared on the accuracy of the model |
3.6.2 位置编码方式对模型性能的影响
为评估位置编码方式对模型性能的影响,通过消融实验,比较静态位置编码(Reg)、动态位置编码(RNN、LSTM、GRU),以及将动态位置编码与静态位置编码结合的组合模型的性能。在BCI Competition Ⅳ Dataset 2a上测试,计算模型平均准确率和Kappa值,结果如表 7所示。采用动态学习位置编码的模型(如RNN、LSTM、GRU)整体上普遍优于静态位置编码模型(Reg),结合动态与静态位置编码的组合模型在某些情况下能够提高模型的稳定性(如Reg_LSTM、Reg_GRU),但其整体性能仍低于纯动态位置编码模型RNN。其中,RNN达到了最高的平均准确率(81.09%)和Kappa值(0.745 3),表明在序列建模任务中,动态位置编码的优势明显。采用静态位置编码的模型(Reg)性能有所下降,说明静态位置编码限制了模型捕捉时序信息的能力。上述实验结果表明动态学习位置编码有助于模型更好地理解和处理复杂的时序数据,从而提升分类性能。
| 方法 Methods |
准确率/% Accuracy/% |
卡帕值 Kappa value |
|||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average | ||
| Reg_RNN | 88.19 | 59.02 | 93.05 | 78.12 | 57.29 | 64.93 | 92.36 | 89.93 | 87.15 | 78.89 | 0.718 6 |
| Reg_LSTM | 87.84 | 64.93 | 94.09 | 80.20 | 59.02 | 67.01 | 94.44 | 90.97 | 87.5 | 80.66 | 0.742 2 |
| Reg_GRU | 88.54 | 62.15 | 94.09 | 83.33 | 58.68 | 66.66 | 93.05 | 89.93 | 87.5 | 80.43 | 0.739 1 |
| Reg | 88.19 | 59.02 | 93.40 | 84.72 | 57.29 | 64.58 | 95.48 | 89.58 | 88.19 | 80.05 | 0.734 0 |
| GRU | 90.62 | 61.45 | 91.66 | 81.25 | 57.29 | 63.88 | 94.44 | 89.58 | 89.93 | 80.01 | 0.736 6 |
| LSTM | 89.93 | 59.72 | 93.05 | 81.94 | 57.63 | 64.58 | 95.13 | 89.93 | 89.58 | 80.16 | 0.735 5 |
| RNN | 90.62 | 61.80 | 94.44 | 84.37 | 57.63 | 66.66 | 94.79 | 89.93 | 89.58 | 81.09 | 0.745 3 |
| Note:the best results of the comparative methods are highlighted in bold. | |||||||||||
4 结论
本研究提出的CRRT模型通过整合CNN、ResRNN和Transformer技术,构建了一种高效的EEG数据分类方法。该模型在局部特征提取、时序建模和全局依赖建模方面的紧密结合,使其在处理复杂的EEG数据时表现出显著优势。特别地,ResRNN通过捕捉时序特征,为Transformer提供了动态位置编码,这一创新显著增强了模型对时间序列的理解能力。相较于传统的静态位置编码,动态位置编码能够根据EEG数据的特性自适应调整位置信息,有效地应对EEG数据的个体差异性、时变性及噪声干扰问题,进一步提升Transformer在EEG数据分类中的建模能力。此外,通过在ResRNN-Transformer模块中实现参数共享,优化了模型的性能表现。整体而言,CRRT模型在EEG数据分类任务中表现出巨大的应用潜力,可为未来脑科学研究和智能系统的发展提供一种新的方案。
| [1] |
JIN J, SUN H, DALY I, et al. A novel classification framework using the graph representations of electroencephalogram for motor imagery based brain-computer interface[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2022, 30: 20-29. DOI:10.1109/TNSRE.2021.3139095 |
| [2] |
LIU B C, CHEN X G, SHI N L, et al. Improving the performance of individually calibrated SSVEP-BCI by task-discriminant component analysis[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2021, 29: 1998-2007. DOI:10.1109/TNSRE.2021.3114340 |
| [3] |
LI J W, BARMA S, MAK P U, et al. Single-channel selection for EEG-based emotion recognition using brain rhythm sequencing[J]. IEEE Journal of Biomedical and Health Informatics, 2022, 26(6): 2493-2503. DOI:10.1109/JBHI.2022.3148109 |
| [4] |
SCHIRRMEISTER R T, SPRINGENBERG J T, FIE-DERER L D J, et al. Deep learning with convolutional neural networks for EEG decoding and visualization[J]. Human Brain Mapping, 2017, 38(11): 5391-5420. DOI:10.1002/hbm.23730 |
| [5] |
LAWHERN V J, SOLON A J, WAYTOWICH N R, et al. EEGNet: a compact convolutional neural network for EEG-based brain-computer interfaces[J]. Journal of Neural Engineering, 2018, 15(5): 056013. DOI:10.1088/1741-2552/aace8c |
| [6] |
TORTORA S, GHIDONI S, CHISARI C, et al. Deep learning-based BCI for gait decoding from EEG with LSTM recurrent neural network[J]. Journal of Neural Engineering, 2020, 17(4): 046011. DOI:10.1088/1741-2552/ab9842 |
| [7] |
SHOEIBI A, SADEGHI D, MORIDIAN P, et al. Automatic diagnosis of schizophrenia in EEG signals using CNN-LSTM models[J]. Frontiers in Neuroinformatics, 2021, 15: 777977. DOI:10.3389/fninf.2021.777977 |
| [8] |
LI H L, DING M, ZHANG R H, et al. Motor imagery EEG classification algorithm based on CNN-LSTM feature fusion network[J]. Biomedical Signal Processing and Control, 2022, 72: 103342. DOI:10.1016/j.bspc.2021.103342 |
| [9] |
SONG Y H, ZHENG Q Q, LIU B C, et al. EEG conformer: convolutional transformer for EEG decoding and visualization[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2023, 31: 710-719. DOI:10.1109/TNSRE.2022.3230250 |
| [10] |
SHE Q S, CHEN T, FANG F, et al. Improved domain adaptation network based on Wasserstein distance for motor imagery EEG classification[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2023, 31: 1137-1148. DOI:10.1109/TNSRE.2023.3241846 |
| [11] |
LOTTE F, BOUGRAIN L, CICHOCKI A, et al. A re- view of classification algorithms for EEG-based brain-computer interfaces: a 10 year update[J]. Journal of Neural Engineering, 2018, 15(3): 031005. DOI:10.1088/1741-2552/aab2f2 |
| [12] |
PADHMASHREE V, BHATTACHARYYA A. Hu- man emotion recognition based on time-frequency analysis of multivariate EEG signal[J]. Knowledge-Based Systems, 2022, 238: 107867. DOI:10.1016/j.knosys.2021.107867 |
| [13] |
BHATTACHARYYA A, TRIPATHY R K, GARG L, et al. A novel multivariate-multiscale approach for computing EEG spectral and temporal complexity for human emotion recognition[J]. IEEE Sensors Journal, 2021, 21(3): 3579-3591. DOI:10.1109/JSEN.2020.3027181 |
| [14] |
SAKHAVI S, GUAN C T, YAN S C. Learning temporal information for brain-computer interface using convolutional neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5619-5629. DOI:10.1109/TNNLS.2018.2789927 |
| [15] |
SHAN X C, CAO J, HUO S D, et al. Spatial-temporal graph convolutional network for Alzheimer classification based on brain functional connectivity imaging of electroencephalogram[J]. Human Brain Mapping, 2022, 43(17): 5194-5209. DOI:10.1002/hbm.25994 |
| [16] |
HONG X L, ZHENG Q Q, LIU L Y, et al. Dynamic joint domain adaptation network for motor imagery classification[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2021, 29: 556-565. DOI:10.1109/TNSRE.2021.3059166 |
| [17] |
HUANG W Q, CHANG W W, YAN G H, et al. EEG-based motor imagery classification using convolutional neural networks with local reparameterization trick[J]. Expert Systems with Applications, 2022, 187: 115968. DOI:10.1016/j.eswa.2021.115968 |
| [18] |
ROY A M. An efficient multi-scale CNN model with intrinsic feature integration for motor imagery EEG subject classification in brain-machine interfaces[J]. Biomedical Signal Processing and Control, 2022, 74: 103496. DOI:10.1016/j.bspc.2022.103496 |
| [19] |
PHAM D T, MOUCEK R. Automatic sleep stage classification by CNN-Transformer-LSTM using single-channel EEG signal [C]//2023 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Piscataway, NJ: IEEE, 2023: 2559-2563.
|
| [20] |
BRUNNER C, LEEB R, MVLLER-PUTZ G R, et al. BCI competition 2008: Graz data set A [Z/OL]. [2024-12-20]. https://lampz.tugraz.at/~bci/database/001-2014/description.pdf.
|
| [21] |
BRUNNER C, LEEB R, MVLLER-PUTZ G R, et al. BCI competition 2008: Graz data set B [Z/OL]. [2024-12-20]. https://www.bbci.de/competition/iv/desc_2b.pdf.
|
| [22] |
ZHENG W L, LU B L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. DOI:10.1109/TAMD.2015.2431497 |
| [23] |
KOELSTRA S, MUHL C, SOLEYMANI M, et al. DEAP: a database for emotion analysis; Using physiological signals[J]. IEEE Transactions on Affective Computing, 2012, 3(1): 18-31. DOI:10.1109/T-AFFC.2011.15 |
| [24] |
ANG K K, CHIN Z Y, WANG C, et al. Filter bank common spatial pattern algorithm on BCI competition Ⅳ datasets 2a and 2b[J]. Frontiers in Neuroscience, 2012, 6: 39. |
| [25] |
MANE R, CHEW E, CHUA K, et al. FBCNet: a multi-view convolutional neural network for brain-computer interface [Z/OL]. arXiv preprint, 2021[2024-12-20]. https://arxiv.org/abs/2104.01233v1.
|
| [26] |
ZHAO H, ZHENG Q Q, MA K, et al. Deep representation-based domain adaptation for nonstationary EEG classification[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(2): 535-545. DOI:10.1109/TNNLS.2020.3010780 |
| [27] |
QIN Y Y, YANG B H, KE S X, et al. M-FANet: multi-feature attention convolutional neural network for motor imagery decoding[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2024, 32. |
| [28] |
LI H Q, ZHANG H D, CHEN Y T. Dual-TSST: a dual-branch temporal-spectral-spatial transformer model for EEG decoding [Z/OL]. arXiv preprint, 2024[2024-12-20]. https://arxiv.org/abs/2409.03251v1.
|
| [29] |
ZHI H Y, YU Z L, YU T Y, et al. A multi-domain co- nvolutional neural network for EEG-based motor imagery decoding[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2023, 31: 3988-3998. DOI:10.1109/TNSRE.2023.3323325 |
| [30] |
LIANG G J, CAO D G, WANG J Q, et al. EISATC-Fusion: inception self-attention temporal convolutional network fusion for motor imagery EEG decoding[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2024, 32: 1535-1545. DOI:10.1109/TNSRE.2024.3382226 |
| [31] |
ZHENG W L, LU B L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. DOI:10.1109/TAMD.2015.2431497 |
| [32] |
ZHENG W L, ZHU J Y, LU B L. Identifying stable patterns over time for emotion recognition from EEG[J]. IEEE Transactions on Affective Computing, 2019, 10(3): 417-429. DOI:10.1109/TAFFC.2017.2712143 |
| [33] |
SONG T F, ZHENG W M, SONG P, et al. EEG emotion recognition using dynamical graph convolutional neural networks[J]. IEEE Transactions on Affective Computing, 2020, 11(3): 532-541. DOI:10.1109/TAFFC.2018.2817622 |
| [34] |
LI Y, ZHENG W M, WANG L, et al. From regional to global brain: a novel hierarchical spatial-temporal neural network model for EEG emotion recognition[J]. IEEE Transactions on Affective Computing, 2022, 13(2): 568-578. DOI:10.1109/TAFFC.2019.2922912 |
| [35] |
ZHONG P X, WANG D, MIAO C Y. EEG-based emotion recognition using regularized graph neural networks[J]. IEEE Transactions on Affective Computing, 2022, 13(3): 1290-1301. DOI:10.1109/TAFFC.2020.2994159 |
| [36] |
YANG L J, WANG Y X, OUYANG R J, et al. Electroencephalogram-based emotion recognition using factorization temporal separable convolution network[J]. Engineering Applications of Artificial Intelligence, 2024, 133. |
| [37] |
LI R, REN C, LI C, et al. SSTD: a novel spatio-temporal demographic network for EEG-based emotion recognition[J]. IEEE Transactions on Computational Social Systems, 2023, 10(1): 376-387. DOI:10.1109/TCSS.2022.3188891 |
| [38] |
LI R, REN C, GE Y Q, et al. MTLFuseNet: a novel emotion recognition model based on deep latent feature fusion of EEG signals and multi-task learning[J]. Knowledge-Based Systems, 2023, 276: 110756. DOI:10.1016/j.knosys.2023.110756 |
| [39] |
LIN K, ZHANG L H, CAI J, et al. DSE-Mixer: a pure multilayer perceptron network for emotion recognition from EEG feature maps[J]. Journal of Neuroscience Methods, 2024, 401: 110008. DOI:10.1016/j.jneumeth.2023.110008 |
| [40] |
RUDAKOV E, LAURENT L, COUSIN V, et al. Multi-task CNN model for emotion recognition from EEG brain maps [C]//2021 4th International Conference on Bio-Engineering for Smart Technologies (BioSMART). Piscataway, NJ: IEEE, 2021: 1-4.
|
| [41] |
CHEN K, JING H C, LIU Q, et al. A novel caps-EEGNet combined with channel selection for EEG-based emotion recognition[J]. Biomedical Signal Processing and Control, 2023, 86: 105312. DOI:10.1016/j.bspc.2023.105312 |
| [42] |
DU Y X, DING H, WU M, et al. MES-CTNet: a novel capsule transformer network base on a multi-domain feature map for electroencephalogram-based emotion recognition[J]. Brain Sciences, 2024, 14(4): 344. DOI:10.3390/brainsci14040344 |



