情绪识别作为脑机接口(Brain-Computer Interface, BCI)技术的关键研究领域[1],近年来受到研究者越来越多的关注。其中,基于脑电图(Electroencephalogram, EEG)的情绪识别广泛应用于心理健康诊断、智能设备交互、教育、驾驶安全等领域,通过分析大脑活动模式来实时监测情绪状态,帮助改善个体体验和提高安全性。EEG信号能够以高时间分辨率捕捉人类大脑的活动特征,为情绪研究提供可靠的数据来源。EEG情绪识别是指从复杂的EEG信号中提取情绪相关特征,从而解码个体的情绪状态。这一技术在心理健康监测、人机交互和情绪驱动的应用中具有重要意义。然而,EEG解码任务面临噪声干扰、个体差异性和低信噪比等诸多挑战。传统的EEG情绪识别方法主要依赖于手工特征提取,如采用常用空间模式(Common Spatial Pattern, CSP)来增强运动想象任务的空间特征[2];采用滤波器组进行频率、节律的提取以及采用小波变换进行时间频率的分析[3];运用支持向量机(Support Vector Machine, SVM)[4-5]进行情绪分类等,这些方法高度依赖人工设计,难以全面捕捉EEG信号的全局时空依赖关系,且在处理复杂、长时间序列的信号时性能受限。
近年来,深度学习技术在EEG情绪识别领域得到广泛应用,其中,使用最多的是卷积神经网络(Convolutional Neural Network, CNN)[6-7]、循环神经网络(Recurrent Neural Network, RNN)[8]和长短时记忆网络(Long Short-Term Memory,LSTM)[9]等。CNN最初在图像处理领域表现出色,而后因其在提取局部空间特征方面的能力突出而被广泛应用于EEG信号处理中。例如,Ozdemir等[10]提出一种利用CNN对EEG信号生成的多光谱拓扑图像进行分类的情绪识别方法。但CNN在捕捉时间依赖关系和动态特征方面存在局限性。因此,Dar等[11]提出将一维卷积递归神经网络与极限学习机相结合的1D-CRNN-ELM架构,该架构能提高帕金森病(Parkinson′s Disease,PD)患者情绪检测的鲁棒性。此外,Xu等[12]提出一种基于LSTM增强的多视图动态情绪图表示模型,通过将电极通道之间的关系集成到EEG信号处理中以提取多维空间拓扑信息,并保留EEG信号丰富的时间信息,从而更好地识别情绪信号。然而,单独使用CNN难以全面捕捉EEG信号的全局时空特征,因此,Chakravarthi等[13]提出结合CNN和LSTM的情绪识别混合模型,郑进港等[14]提出一种基于动态图卷积神经网络-双向长短时记忆网络的模型。这些结合方法多数采用CNN或LSTM,其中CNN容易发生梯度消失问题,而LSTM在传统上采用向量记忆单元,存储量小,记忆力较弱,也容易发生梯度消失问题,且对EEG信号幅值的微小变化不敏感,难以准确建模EEG信号的渐进性变化。
为实现EEG信号局部与全局时空特征的高效融合,并增强模型对微小信号变化和长程动态的敏感性,同时解决传统LSTM中梯度消失与记忆容量受限的问题,本研究提出一种混合时空卷积和残差扩展型长短时记忆网络(Residual Extended Long Short-Term Memory,RxLSTM)模型CNN-RxLSTM。其中,CNN负责提取EEG信号的局部时空特征;xLSTM[15]则采用矩阵记忆单元(相比于LSTM具备更强的存储能力),并利用指数激活函数,提高对微小变化的敏感性,从而更精准地捕获EEG信号的细微差异。同时,RxLSTM通过双向结构增强对EEG信号全局时空依赖的学习能力,并借助残差机制解决梯度消失的问题,使反向传播能够深入浅层网络,以提升深层模型的训练稳定性(图 1)。
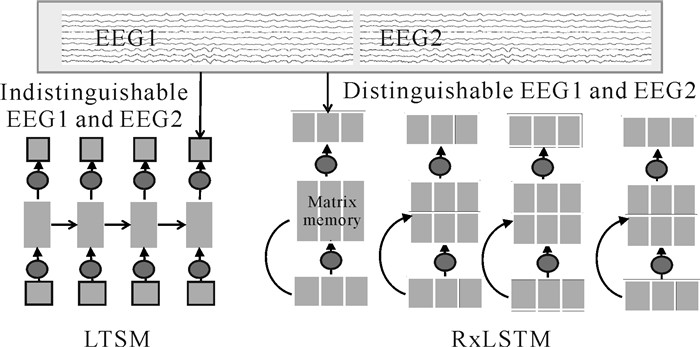
|
| 图 1 RxLSTM功能 Fig.1 RxLSTM function |
1 方法 1.1 数据预处理
EEG数据以C×T的矩阵形式呈现,其中C是电极通道数,T是时间采样点数。为保证数据质量并适应后续处理,需要对数据进行带通滤波和分数标准化处理,带通滤波处理能够有效抑制脑电信号中不相关的频率成分,保留关键信号特征;分数标准化处理能够消除不同电极通道和样本间的量纲差异。首先,对数据进行0.5-40.0 Hz的带通滤波处理,以去除高频和低频噪声,同时保留与任务相关的脑电节律;然后对滤波后的数据进行分数标准化处理,Xnorm=(Xi-μ)÷σ(其中,Xnorm是标准化后的信号,Xi是输入信号,μ和σ分别为均值和标准差),从而确保各个电极通道的信号具有统一的尺度,以减少样本间的波动性和非平稳性。
1.2 CNN-RxLSTM模型基于CNN-RxLSTM的EEG情绪识别模型主要包含3个模块:时空卷积模块(CNN)、xLSTM模块、分类器模块。首先,时空卷积模块从原始的EEG数据中提取初步的时空特征。其次,xLSTM模块通过引入双向时序处理和残差连接的mLSTM结构,完成正反向处理(Block为奇数时进行正向序列处理,为偶数时则进行反向序列处理)的周期性建模。其中,xLSTM模块的核心为矩阵LSTM块对(Matrix Long Short-Term Memory BlockPair,mLSTM BlockPair),由相邻的两个mLSTM Block构成,通过堆叠多层BlockPair,逐步提取多层次的高级时空特征,捕获全局时空依赖和复杂的时空关系。最后,分类器模块通过全连接层将高维特征映射为最终的EEG类别概率,实现情绪状态的准确分类(图 2)。
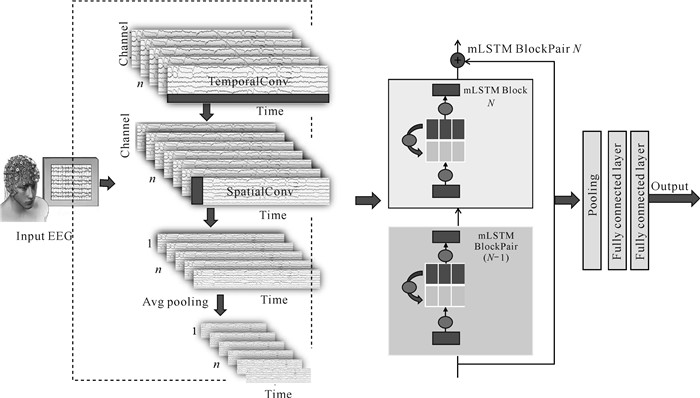
|
| 图 2 CNN-RxLSTM模型 Fig.2 CNN-RxLSTM model |
1.2.1 时空卷积模块
为适应EEG数据的复杂性,将二维卷积分解成一维的时间卷积层和空间卷积层,分别在时间和空间维度提取特征,以捕获不同特征并处理EEG数据的复杂结构。
时间卷积层通过捕捉时序动态变化,建模EEG信号的时间依赖关系:
| $ \text { TemporalFeatures }=\text { TemporalConv }\left(X_t, W_t\right), $ | (1) |
其中,Xt是输入信号在时间维度上的特征,Wt是时间卷积核的权重。
空间卷积层通过捕捉空间依赖性,建模电极通道间的关系:
| $ \text { SpatialFeatures }=\text { SpatialConv }\left(X_s, W_s\right), $ | (2) |
其中,Xs是输入信号在空间维度上的特征,Ws是空间卷积核的权重。
为优化训练过程,采用归一化来提高训练的稳定性,并结合ELU激活函数增强非线性表达能力。同时,通过平均池化操作来平滑时间特征,这不仅能降低计算复杂度,而且能解决过拟合问题。随后,通过通道压缩和特征置换,将高维特征映射为每个时间点的特征向量,并将其作为独立单元输入后续模块,为情绪识别任务奠定基础。
1.2.2 xLSTM模块xLSTM模块是由多个mLSTM Block组成的堆叠结构,mLSTM Block的具体设计如图 3(a)所示,图 3(b)是对图 3(a)中mLSTM层的具体描述。首先,将卷积后的特征输入到xLSTM模块进行向上投影(即升维),投影因子(PF)为2,分为两个并行路径,其中一路输入外部输出门,另一路作为mLSTM单元的输入,若mLSTM Block序号为偶数时则进行翻转,使其进行反向处理。在mLSTM单元内部中,NH=n表示xLSTM模块包含n个注意力头,每个注意力头内部配备独立的门控机制,包括输入门(i)和遗忘门(f),从而提升时序建模能力。在处理过程中,输入特征首先通过块对角投影矩阵(BS)从输入中生成查询(q)和键(k),而值(v)直接传递至序列混合模块,以捕获长程依赖关系。其次,mLSTM的输出经过组归一化(Group Normalization, GN)处理以稳定训练,并通过逐元素加法与可学习的跳跃连接(LSkip)结合,进一步增强特征整合能力,输出结果再与外部输出门进行按组件相乘的门控操作。最后,输出结果投影降维回原始维度。
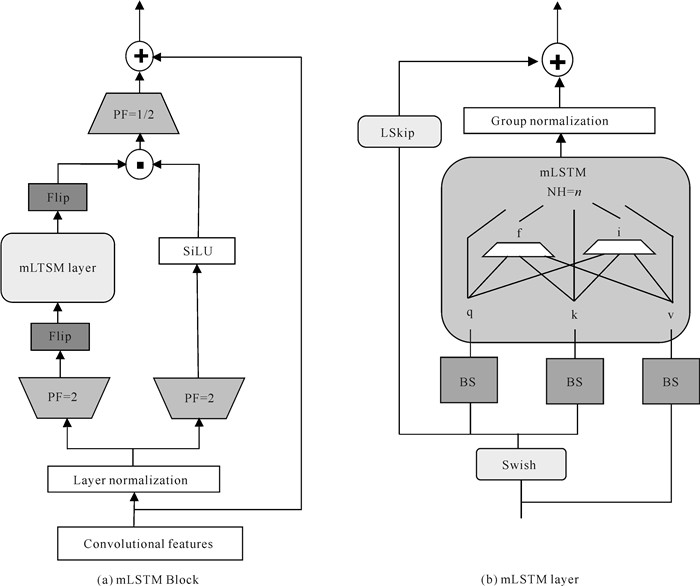
|
| 图 3 mLSTM结构图 Fig.3 Diagram of mLSTM structure |
① 特征输入
输入到xLSTM模块的特征形状为(B, C1, L1),其中B是批次大小,C1是卷积层处理后的通道数,L1是时间步长。这些特征是经过时空卷积模块处理后得到的,已携带空间、时间和位置编码信息,方便后续处理。
② 双向时间特征提取
当Block序号为奇数时,按时间顺序从第一个时间步到最后一个时间步处理序列,捕捉前向时间依赖关系。在每一个Block中引入指数激活函数,指数激活函数对输入值的变化非常敏感,可以有效地放大特定的特征或响应,这使得模型能更好地捕捉到EEG信号中的关键特征和变化。正向处理对应的公式如下:
| $ i_t=\exp \left(W_i^{\mathrm{T}} X_t+b_i\right), $ | (3) |
| $ f_t=\exp \left(W_f^{\mathrm{T}} X_t+b_f\right), $ | (4) |
| $ o_t=\sigma\left(W_o^{\mathrm{T}} X_t+b_o\right), $ | (5) |
| $ n_t=f_t n_{t-1}+i_t k_t, $ | (6) |
| $ C_t^{f w}=f_t C_{t-1}^{f w}+i_t v_t k_t^{\mathrm{T}}, $ | (7) |
| $ h_t^{f w}=o_t \odot\left(C_t^{f w} q_t / \max \left\{\left|n_t^{\mathrm{T}} q_t\right|, 1\right\}\right), $ | (8) |
其中,it表示输入门,决定当前输入对记忆的影响;Xt是第t个时间步的输入特征;WiT、WfT和WoT是权重矩阵;bi、bf和bo是偏置项;exp为指数线性单元激活函数;σ为sigmoid激活函数。nt表示t时刻的稳定机制;nt-1表示t-1时刻的稳定机制,防止数值过大溢出;kt表示t时刻的键向量;vt表示t时刻的值向量;ft表示遗忘门,用来控制前一时刻记忆对当前时刻的影响;ot为输出门,决定当前时刻的输出。Ctfw表示t时刻的前向记忆单元的状态,Ct-1fw表示t-1时刻前向记忆单元的状态,htfw是第t个时间步的前向隐藏状态,qt表示t时刻的查询向量。
当Block序号为偶数时,将序列顺序反转,按时间顺序从最后一个时间步到第一个时间步处理序列,捕捉反向时间依赖关系。反向处理对应的公式如下:
| $ C_t^{b w}=f_t C_{t+1}^{b w}+i_t v_t k_t^{\mathrm{T}}, $ | (9) |
| $ h_t^{b w}=o_t \odot\left(C_t^{b w} q_t / \max \left\{\left|n_t^{\mathrm{T}} q_t\right|, 1\right\}\right), $ | (10) |
其中,Ctbw表示t时刻反向处理的记忆单元状态,Ct+1bw表示t+1时刻反向处理的记忆单元状态,htbw表示第t个时间步反向处理的隐藏状态,其余符号与正向处理定义一致。反向处理完成后,特征顺序将翻转还原为正向格式,便于与正向特征对齐。
③ BlockPair堆叠与残差设计
残差的BlockPair包含两个Block,将其进行正向和反向处理,并通过残差连接实现内部特征的融合,不同Block的特征相互补充。BlockPair(X)=X+BlockPair(X),其中X表示输入特征,BlockPair(X)表示经过正向和反向处理序列后得到的特征。
每个BlockPair完成正向和反向处理序列的完整周期后,其输出直接作为下一层BlockPair的输入。BlockPair堆叠的特征流动公式如下:
| $ h_{\mathrm{xLSTM}}=N \times(\text { mLSTM BlockPairs }), $ | (11) |
其中,hxLSTM表示最终输出的特征,N表示mLSTM BlockPair的数量。
1.2.3 分类器模块xLSTM模块提取的特征hxLSTM包含多层次的时空信息,这些特征经过分类器模块的两层全连接层处理后,映射到目标类别数M。通过Softmax函数,将特征变换为概率分布,用于确定样本的最终分类结果,计算公式如下:
| $ \hat{y}=\operatorname{Softmax}\left(W_{f_c} h_{\mathrm{xLSTM}}+b_{f_c}\right), $ | (12) |
其中,
分类器模块采用交叉熵损失函数来评估预测结果与真实标签之间的差异,计算公式如下:
| $ \text { Loss }=-\frac{1}{N_b} \sum\limits_{i=1}^{N_b} \sum\limits_{j=1}^M y_{i, j}^{\log \left(\hat{y}_{i, j}\right)}, $ | (13) |
其中,Nb表示批次大小,M表示类别总数,yi, j表示第i个样本第j类的真实标签,
为验证CNN-RxLSTM模型的性能优势,分别在SEED数据集[16]和DEAP数据集[17]上进行实验。
SEED数据集:该数据集从电影中挑选15个情感片段,分为积极、中性和消极3类,每类有5个片段。选取15名健康受试者(12名女性和3名男性,年龄为22-25岁)参与实验,通过62通道的EEG系统记录脑电信号。每位受试者进行3次实验,EEG数据分为2 s的片段,作为独立的数据样本。假设情感刺激能够在2 s内稳定地诱发脑电特征,并忽略个体间的微观生理差异。
DEAP数据集:该数据集挑选40个视频片段为刺激,通过觉醒度和愉悦度评分进行情感标注,选取32名受试者(16名男性和16名女性,年龄为22-37岁)的EEG数据,使用32通道的EEG设备进行记录。对EEG数据进行下采样,采样率调整为128 Hz,并经过4-45 Hz的带通滤波去噪,处理时提取基线与情感信号的差分熵特征差异。假设情感状态在实验过程中相对稳定,并且4-45 Hz频段的EEG特征能够有效表征情感变化。
2.2 实验设置实验在NVIDIA RTX 3090 GPU上进行,使用PyTorch框架,数据处理的核心工具为MATLAB R2022a,依托其信号处理工具箱(Signal Processing Toolbox)提供的专业滤波与频谱分析功能,以及EEGLAB工具箱的高级信号处理能力,实现脑电信号的批量化处理。数据被划分为训练集(80%)和测试集(20%),训练参数包括批量大小(128)、学习率(0.000 2)、Adam优化器(beta 1=0.5,beta 2=0.999)。损失函数采用交叉熵损失用于分类,评价指标包括分类准确率和Kappa系数。分类准确率=正确分类的样本数/总样本数;Kappa系数的计算公式为
选取多种具有代表性的方法作为基线模型,这些基线模型涵盖了传统分类器、图神经网络、多维度特征融合模型等方法,全面展示了不同方法在处理EEG信号中的复杂时空依赖关系的优缺点,从而验证CNN-RxLSTM模型的性能优势。传统的SVM方法[16],其结构简单且在小规模数据集中训练速度快,但依赖于手工特征提取,难以自动提取EEG信号的复杂时空特征,且无法捕捉EEG信号的时间动态性。图神经网络方法有动态图卷积神经网络-双向长短时记忆网络(DGCNN-BiLSTM)[14]、ERGL[18]等。其中,DGCNN-BiLSTM通过DGCNN动态学习电极通道间的空间依赖关系,并利用BiLSTM捕捉时序特征,适应情绪发生过程中通道关系的变化。然而,该模型依赖于图卷积建模空间,难以有效提取局部时空特征,且存在长时序依赖弱化和计算复杂度较高的问题。基于图卷积网络(GCN)和ERGL的模型,既能提取EEG信号的空间特征,又能捕捉时间依赖关系,通过构建二维网格矩阵,能更好地建模空间相关性。但GCN依赖手工构造的邻接矩阵,难以动态适应EEG通道间的复杂时变关系,且LSTM在长时序建模时仍面临梯度消失的问题。多尺度建模方法有3DCNN-ConvLSTM[19]、3D-CRU[20]等。3DCNN-ConvLSTM通过四维特征结构与动态时间信息强化多维度情绪特征建模,3D-CRU则通过多尺度三维卷积与门控循环单元(GRU)联合提取时空频域特征,这两种方法均面临长时序依赖建模不足(GRU梯度消失)和计算复杂度高的问题,难以满足长时间EEG信号处理的需求。此外,Dual-TSST(Dual-branch Temporal-Spectral-Spatial Transformer)模型[21]结合了CNN和Transformer,能有效提取EEG信号的时空和时频特征,但Transformer计算量较大,难以高效处理长时间的EEG信号。本研究提出的CNN-RxLSTM通过残差xLSTM模块既能有效解决LSTM、GRU梯度消失的问题,增强对情绪长程动态的建模能力,同时又通过轻量级CNN和RxLSTM的架构设计,降低了计算复杂度,解决了三维卷积与复杂时序模块的计算瓶颈。
2.4 结果与分析为验证CNN-RxLSTM模型的性能优势,将其在两个公开数据集上进行实验,并与多种模型进行对比。在SEED数据集上的实验结果表明,CNN-RxLSTM模型在情绪识别任务中的表现远超DGCNN-BiLSTM、ERGL、Dual-TSST等主流模型,其分类准确率和Kappa系数分别为98.15%和0.972 2,相比于目前最优模型Dual-TSST,分类精度提升了1.55%,展现了该模型在复杂信号处理任务中的优越性能(表 1)。此外,在相同实验环境下,还设计了与CNN-LSTM模型的对比实验,结果表明CNN-RxLSTM在EEG情绪识别任务中表现更优,验证了RxLSTM模型的有效性(表 1)。在DEAP数据集上的实验结果表明,CNN-RxLSTM模型也展现出卓越的性能,效价分类准确率和唤醒分类准确率分别为94.60%和95.89%,相较于目前最优模型3D-CRU,在效价分类准确率和唤醒分类准确率上分别提升了1.59%和1.68%,总体优于SSTD、3DCNN-ConvLSTM、3D-CRU和ERGL等模型(表 2)。
| 模型 Model |
分类准确率/% Classification accuracy/% |
Kappa系数 Kappa coefficient |
| DGCNN-BiLSTM[14] | 92.03 | — |
| SVM[16] | 83.99 | 0.791 2 |
| ERGL[18] | 94.92 | — |
| Dual-TSST[21] | 96.65 | — |
| STRNN[22] | 89.50 | — |
| DGCNN[23] | 90.40 | 0.856 0 |
| R2G-STNN[24] | 93.38 | 0.900 7 |
| RGNN[25] | 94.24 | 0.913 6 |
| Conformer[26] | 95.30 | 0.929 5 |
| CNN-LSTM | 85.35 | 0.779 8 |
| CNN-RxLSTM | 98.15 | 0.972 2 |
2.5 消融实验
使用SEED数据集测试不同数量的RxLSTM Block块数和xLSTM Block块数对分类准确率的影响(图 4)。整体来看,RxLSTM的性能优于xLSTM,表明残差结构能够有效解决梯度消失的问题,提高模型的训练效率和泛化能力。当RxLSTM Block块数为6时,分类准确率为95.93%;随着Block块数的增加,分类准确率缓慢上升,直到Block块数为8时,分类准确率达到最高(98.15%),而后逐渐下降;当Block块数为12时,分类准确率下降至37.06%,表明过多的Block块可能会导致过拟合,显著削弱模型的性能。因此,RxLSTM的最佳Block块数为8,此时分类准确率能保持在较高水平,且模型的复杂度相对适中。
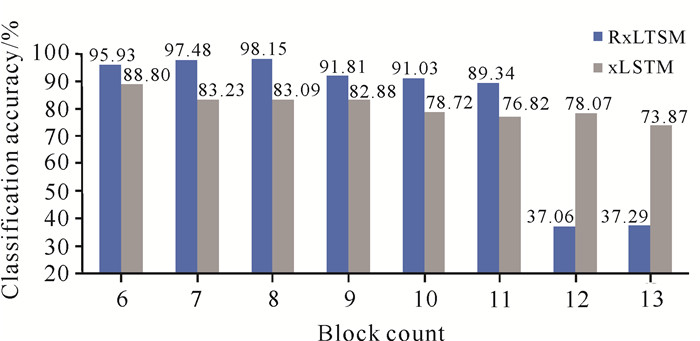
|
| 图 4 RxLSTM Block块数和xLSTM Block块数对分类准确率的影响 Fig.4 Impact of RxLSTM Block count and xLSTM Block count on classification accuracy |
3 结论
本研究提出基于混合时空卷积与残差xLSTM的EEG情绪识别模型CNN-RxLSTM,通过分层设计实现对EEG信号中复杂时空特征的自动提取和长时序依赖建模。该模型首先利用时空卷积模块提取初步的时间和空间特征;然后引入xLSTM模块通过双向时序处理与残差连接,增强全局依赖建模能力;最后由分类器模块实现情绪状态的精准分类。实验结果表明,CNN-RxLSTM模型的分类性能和稳定性均显著优于传统模型,验证了其在EEG解码中的有效性,为情绪识别及相关领域提供了高效的解决方案。然而,该模型在处理更复杂的非线性关系和高维特征交互方面仍存在不足,其在跨数据集或跨被试条件下的泛化能力亦需进一步验证。后续研究可考虑结合图神经网络等先进方法,以更好地捕捉电极间复杂的拓扑关系,并优化特征建模结构,同时扩展模型在其他脑电任务中的应用,进一步提升其泛化性和适用性。
| [1] |
LI J W, BARMA S, MAK P U, et al. Single-channel selection for EEG-based emotion recognition using brain rhythm sequencing[J]. IEEE Journal of Biomedical and Health Informatics, 2022, 26(6): 2493-2503. DOI:10.1109/JBHI.2022.3148109 |
| [2] |
ANG K K, CHIN Z Y, WANG C, et al. Filter bank common spatial pattern algorithm on BCI competition Ⅳ datasets 2a and 2b[J]. Frontiers in Neuroscience, 2012, 6: 39. |
| [3] |
CHEN X G, WANG Y J, GAO S K, et al. Filter bank canonical correlation analysis for implementing a high-speed SSVEP-based brain-computer interface[J]. Journal of Neural Engineering, 2015, 12(4): 046008. DOI:10.1088/1741-2560/12/4/046008 |
| [4] |
WANG X W, NIE D, LU B L. EEG-based emotion recognition using frequency domain features and support vector machines [M]//Berlin, Heidelberg: Springer, 2011: 734-743.
|
| [5] |
BAZGIR O, MOHAMMADI Z, HABIBI S A H. Emo- tion recognition with machine learning using EEG signals [C]//2018 25th National and 3rd International Iranian Conference on Biomedical Engineering (ICBME). Piscataway, NJ: IEEE, 2018: 1-5.
|
| [6] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition [C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ: IEEE, 2016: 770-778.
|
| [7] |
SCHIRRMEISTER R T, SPRINGENBERG J T, FIE-DERER L D J, et al. Deep learning with convolutional neural networks for EEG decoding and visualization[J]. Human Brain Mapping, 2017, 38(11): 5391-5420. DOI:10.1002/hbm.23730 |
| [8] |
WILLIAMS R J, ZIPSER D. A learning algorithm for continually running fully recurrent neural networks[J]. Neural Computation, 1989, 1(2): 270-280. DOI:10.1162/neco.1989.1.2.270 |
| [9] |
GRAVES A. Supervised sequence labelling with recurrent neural networks[M]. Berlin, Heidelberg: Springer, 2012.
|
| [10] |
OZDEMIR M A, DEGIRMENCI M, IZCI E, et al. EEG-based emotion recognition with deep convolutional neural networks[J]. Biomedical Engineering/Biomedizinische Technik, 2021, 66(1): 43-57. DOI:10.1515/bmt-2019-0306 |
| [11] |
DAR M N, AKRAM M U, YUVARAJ R, et al. EEG-based emotion charting for Parkinson's disease patients using Convolutional Recurrent Neural Networks and cross dataset learning[J]. Computers in Biology and Medicine, 2022, 144: 105327. DOI:10.1016/j.compbiomed.2022.105327 |
| [12] |
XU G X, GUO W H, WANG Y J. LSTM-enhanced multi-view dynamical emotion graph representation for EEG signal recognition[J]. Journal of Neural Engineering, 2023, 20(3): 036038. DOI:10.1088/1741-2552/ace07d |
| [13] |
CHAKRAVARTHI B, NG S C, EZILARASAN M R, et al. EEG-based emotion recognition using hybrid CNN and LSTM classification[J]. Frontiers in Computational Neuroscience, 2022, 16: 1019776. DOI:10.3389/fncom.2022.1019776 |
| [14] |
郑进港, 杨俊. 基于动态图卷积神经网络和BiLSTM的情绪识别[J]. 陕西理工大学学报(自然科学版), 2024, 40(5): 67-73, 82. |
| [15] |
BECK M, PÖPPEL K, SPANRING M, et al. xLSTM: extended long short-term memory [Z/OL]. [2025-01-12]. https://arxiv.org/abs/2405.04517?context=cs.
|
| [16] |
ZHENG W L, LU B L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. DOI:10.1109/TAMD.2015.2431497 |
| [17] |
KOELSTRA S. DEAP: a database for emotion Analysis; Using physiological signals[J]. IEEE Transactions on Affective Computing, 2012, 3(1): 18-31. DOI:10.1109/T-AFFC.2011.15 |
| [18] |
ZHENG F, HU B, ZHENG X W, et al. Spatial-temporal features-based EEG emotion recognition using graph convolution network and long short-term memory[J]. Physiological Measurement, 2023, 44(6): 065002. DOI:10.1088/1361-6579/acd675 |
| [19] |
房好田. 基于深度学习的脑电情绪识别研究[D]. 曲阜: 曲阜师范大学, 2024.
|
| [20] |
DONG H, ZHOU J, FAN C H, et al. Multi-scale 3D-CRU for EEG emotion recognition[J]. Biomedical Physics & Engineering Express, 2024, 10(4): 045018. |
| [21] |
LI H Q, ZHANG H D, CHEN Y T. Dual-TSST: a dual-branch temporal-spectral-spatial transformer model for EEG decoding [Z/OL]. [2025-01-25]. https://arxiv.org/abs/2409.03251?context=cs.
|
| [22] |
ZHANG T, ZHENG W M, CUI Z, et al. Spatial-temporal recurrent neural network for emotion recognition[J]. IEEE Transactions on Cybernetics, 2019, 49(3): 839-847. DOI:10.1109/TCYB.2017.2788081 |
| [23] |
SONG T F, ZHENG W M, SONG P, et al. EEG emotion recognition using dynamical graph convolutional neural networks[J]. IEEE Transactions on Affective Computing, 2020, 11(3): 532-541. DOI:10.1109/TAFFC.2018.2817622 |
| [24] |
LI Y, ZHENG W M, WANG L, et al. From regional to global brain: a novel hierarchical spatial-temporal neural network model for EEG emotion recognition[J]. IEEE Transactions on Affective Computing, 2022, 13(2): 568-578. DOI:10.1109/TAFFC.2019.2922912 |
| [25] |
ZHONG P X, WANG D, MIAO C Y. EEG-based emotion recognition using regularized graph neural networks[J]. IEEE Transactions on Affective Computing, 2022, 13(3): 1290-1301. DOI:10.1109/TAFFC.2020.2994159 |
| [26] |
SONG Y H, ZHENG Q Q, LIU B C, et al. EEG conformer: convolutional transformer for EEG decoding and visualization[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2022, 31: 710-719. |
| [27] |
LI R, REN C, LI C, et al. SSTD: a novel spatio-temporal demographic network for EEG-based emotion recognition[J]. IEEE Transactions on Computational Social Systems, 2023, 10(1): 376-387. DOI:10.1109/TCSS.2022.3188891 |
| [28] |
LI R, REN C, GE Y Q, et al. MTLFuseNet: a novel emotion recognition model based on deep latent feature fusion of EEG signals and multi-task learning[J]. Knowledge-Based Systems, 2023, 276: 110756. DOI:10.1016/j.knosys.2023.110756 |
| [29] |
YUVARAJ R, THAGAVEL P, THOMAS J, et al. Comprehensive analysis of feature extraction methods for emotion recognition from multichannel EEG recordings[J]. Sensors, 2023, 23(2): 915. DOI:10.3390/s23020915 |
| [30] |
AN Y L, HU S H, DUAN X Y, et al. Electroencephalo- gram emotion recognition based on 3D feature fusion and convolutional autoencoder[J]. Frontiers in Computational Neuroscience, 2021, 15: 743426. DOI:10.3389/fncom.2021.743426 |



