核电为低碳清洁能源,有助于碳达峰和碳中和目标的实现[1]。然而,核电站废热排放形成的温排水可使得周边海域水温升高[2-4]。因此,准确刻画温排水扩散规律具有重大意义。
温排水扩散规律研究方法包括理论分析、数值模拟、实地监测等,其中温排水数值模拟具有效费比高、可重现、便捷等优点,但对物理假设、参数和验证的要求较高[5-7]。Lowe等[8]利用构建的数学模型对河口水域的电厂温排水扩散现象进行研究,发现温排水扩散中羽流效应起主导作用。Zeng等[9]结合数值模拟与实际观测数据,探究了电厂热排放对周边海域水温的影响,发现温升最大区域集中在排水口附近,且主要影响局限于海水表层,随着海水深度的增加其影响范围迅速缩小。Jiang等[10]模拟了不同核电站温排水在不同季节的扩散规律,发现冬季的中温升面积远大于夏季。不同季节的环境背景温度也是影响海水温排水扩散效果的关键因素[11-13]。Ren等[14]通过温排水扩散数学模型,探究不同参数条件下温排水热排放对周边水域产生的影响,发现温排水对近区河体温度的影响较小,且温度影响衰减较快。Kong等[15]基于数学模型对不同工况下的温升羽流扩散范围进行研究,指出在排水流速减半时,表面热羽流的扩散面积减少了一半以上。涂向阳等[16]基于一系列水动力参数的验证试验,针对潮汐动力主导下的河湾区域温排水,分析了不同取、排水口布置条件下的温排水运动和扩散规律,发现取、排水口的位置对温升面积的影响显著。段亚飞等[17]通过对比温排水水槽试验与数值模拟的结果,指出水体温度对扩散系数表现出较高的敏感性。汪求顺等[18]分析了强潮海域温排水扩散特性,得出横纵向热扩散系数为5.73。
综上所述,现有的温排水数值模拟技术可以较好地反映温排水扩散规律,然而核电站近区河流排涝对温排水扩散规律的影响研究较少。在综合考虑河口对温排水输运和扩散作用时,潮流特性与近区河口水文条件对温升面积有较大影响[19]。此外,不同温排水工况也会导致温升面积出现明显差异[20]。田湾核电站温排水扩散海域近区有一条流量较大的河流——排淡河,其设计排涝流量与田湾核电站排水流量相当。本研究基于田湾核电站温排水排放方案及附近海域水动力特征,构建温排水三维数学模型,通过设置排淡河不同排水条件,分析其对温排水扩散近区流场及扩散规律的影响,以期为温排水环境效益评估和海洋生态保护提供参考。
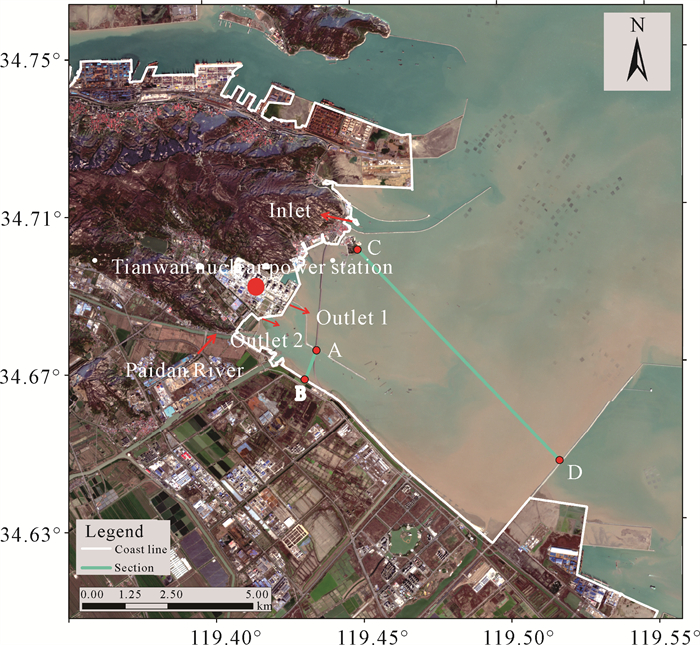
1 材料与方法 1.1 研究区域概况田湾核电站位于江苏省连云港市连云区,研究区域位于连云区云台山脉与徐圩港区防波堤环抱构成的半开放海湾内(图 1),海水交换能力和温排水扩散能力较差,热能富集改变了温排水用海海域的海洋生态环境。
|
| 图 1 研究区域概况及立面位置示意图 Fig.1 Research area overview and elevation position diagram |
田湾核电站全功率运行的排水流量约为500 m3/s,其中排口1排水流量约为100 m3/s,排口2排水流量约为400 m3/s,排水温升均为10 ℃。排淡河位于田湾核电站以西,排淡河入海口与排口2的直线距离仅约1 km,位于田湾核电站温排水近区。由于排水导流堤的束缚,田湾核电站温排水和排淡河水均由宽约900 m的口门排海。
排淡河的径流流量具有明显的季节性,6-9月流量较大,其中7月最大,排淡河排海节制闸的设计流量为523.6 m3/s (20年一遇标准)。排淡河流域年平均降水量901.7 mm,年最大降水量1 374.3 mm (2000年),最大日降水量264.4 mm (1976年),降水时空分布不均,年际变化较大。排淡河流域面积34.4 km2,山丘区与平原区流域面积相当,降水后山洪进入平原河道和洼地滞蓄,洪水由排淡河排海节制闸入海,排水周期一般为2-3潮。
1.2 温排水扩散规律研究方法 1.2.1 水温平面分布规律为更好描述研究海域冬季的水温平面分布特征,根据2021年冬季9个水温测站(T3-T5、T8-T10、T12-T14)实测数据,采用Kriging插值法在已知数据点之间估算未知数据点的值,绘制研究区域冬季水温平面分布图。
1.2.2 水温立面分布规律基于三维温排水数学模型,选取排水导流堤处立面AB (宽约900 m)和羊山岛至徐圩港区防波堤的立面CD (宽约8 550 m),以涨急时刻为例,分别绘制排淡河523.6 m3/s流量工况下立面AB和CD的温度分布图,以刻画研究区域的水温立面分布规律,立面AB和CD位置见图 1。
1.2.3 河流排涝对温排水扩散的影响通过模拟15 d (一个全潮周期)的温排水扩散过程,研究排淡河不同排水流量对温升区面积的影响。由于排淡河无热源,故认为排淡河排水温升为0 ℃,河流向海域排水可起到冷却温排水、减小温升区范围的作用。然而,田湾核电站温排水近区河流向海域排水还可能使各温升区面积变化、位置移动,因此,为准确界定田湾核电站近区河流排水对温排水扩散的影响,将核电站排水流量设定为500 m3/s,以排淡河排海节制闸的设计流量为参考,设置每40 m3/s为一级,分别预测4、3、2、1 ℃温升区面积的变化。针对排淡河不同流量工况,通过温升包络图分析田湾核电站温排水各温升区范围的变化情况。
1.3 温排水三维数学模型建立 1.3.1 控制方程① 潮流连续方程
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=S 。$ | (1) |
② 潮流动量方程
| $ \begin{gathered} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}-f v=-\frac{1}{\rho} \frac{\partial P}{\partial x}+ \\ \frac{\partial}{\partial x}\left(E \frac{\partial u}{\partial x}\right)+\frac{\partial}{\partial y}\left(E \frac{\partial u}{\partial y}\right)+\frac{\partial}{\partial z}\left(E \frac{\partial u}{\partial z}\right)+u_s S, \end{gathered} $ | (2) |
| $ \begin{gathered} \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}+f u=-\frac{1}{\rho} \frac{\partial P}{\partial y}+ \\ \frac{\partial}{\partial x}\left(E \frac{\partial v}{\partial x}\right)+\frac{\partial}{\partial y}\left(E \frac{\partial v}{\partial y}\right)+\frac{\partial}{\partial z}\left(E \frac{\partial v}{\partial z}\right)+v_s S, \end{gathered} $ | (3) |
| $ \begin{gathered} \frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z}=-\frac{1}{\rho} \frac{\partial P}{\partial z}+ \\ \frac{\partial}{\partial x}\left(E \frac{\partial w}{\partial x}\right)+\frac{\partial}{\partial y}\left(E \frac{\partial w}{\partial y}\right)+\frac{\partial}{\partial z}\left(E \frac{\partial w}{\partial z}\right)-g+w_s S, \end{gathered} $ | (4) |
| $ \;\;\;\;\;\; \frac{\partial \Delta T}{\partial t}+u \frac{\partial \Delta T}{\partial x}+v \frac{\partial \Delta T}{\partial y}+w \frac{\partial \Delta T}{\partial z}= \\ \frac{\partial}{\partial x}\left(D \frac{\partial \Delta T}{\partial x}\right)+\frac{\partial}{\partial y}\left(D \frac{\partial \Delta T}{\partial y}\right)+\frac{\partial}{\partial z}\left(D \frac{\partial \Delta T}{\partial z}\right)- \\ \frac{K_s \Delta T}{\rho c_p(h+\zeta)}+\Delta T_s S。$ | (5) |
式中,S为源汇项;u、v、w分别为流速矢量沿x、y、z方向的流速分量,单位m/s;t为时间,单位s;f为科氏参量(f=2ωsinφ,ω为地球自转的角速度,φ为纬度);ρ为密度,单位kg/m3;P为压强,单位Pa;E为水流广义扩散系数,单位m2/s;us、vs、ws分别为源项在x、y、z方向的流速分量,单位m/s;g为重力加速度,单位m/s2;ΔT为水体超温,ΔT=T-T∞,T为水温,T∞为自然水温,单位℃;D为广义物质扩散系数;Ks为表面综合散热系数;cp为水的比热,单位J/(kg·℃);h为总水深,单位m;ζ为相对于x、o、y坐标平面的水位,单位m;ΔTs为源项的超温,单位℃。
1.3.2 定解条件① 流场初始条件
初始条件是指在计算的起始时刻,计算域内各点的流速值及水位值,可用以下公式表示。
| $ \left\{\begin{array}{l} \zeta\left(x, y, t_0\right)=\zeta_0(x, y) \\ u\left(x, y, z, t_0\right)=u_0(x, y, z) \\ v\left(x, y, z, t_0\right)=v_0(x, y, z) \\ w\left(x, y, z, t_0\right)=w_0(x, y, z) \end{array}\right. , $ | (6) |
式中,ζ0、u0、v0、w0是在t0时刻的初始输入值,一般情况下,初始条件不一定十分准确,但是根据数学模型的特点,在经过一段时间的计算后,初始值带来的误差会逐步消失。模型中将初始条件定义为零值。
② 流场边界条件
固边界条件:通常指陆地边界。在垂向上,所有在固边界上的流体流动的变量都被认为是0。
开边界条件:采用潮汐调和预报潮位过程作为外海开边界条件;田湾核电站排水开边界条件为排口1水量100 m3/s,排口2水量400 m3/s。
动边界条件:近岸区域时常分布有潮滩,水陆交界的位置会随着潮位的涨落而变化,潮滩间歇性地淹没和露出,因此河口海岸区域的水动力数值模拟通常需要考虑动边界的影响。一般采用干湿判别法来确定动边界,反映潮滩的干湿特征。
③ 温度场定解条件
边界条件:对于岸边界采用绝热条件,对于水边界按照式(7)计算。大气温度、湿度、风应力等因素是影响海气热交换的重要因素,上述要素资料从欧洲中期天气预报中心(https://cds.climate.copernicus.eu/)获取,精度为0.25°×0.25°。
| $ \begin{aligned} & \quad \frac{\partial[(h+\zeta) \Delta T]}{\partial t}+\frac{\partial[(h+\zeta) u \Delta T]}{\partial x}+ \\ & \frac{\partial[(h+\zeta) v \Delta T]}{\partial y}=0 。\end{aligned} $ | (7) |
初始条件:在计算域内采用零温升条件。
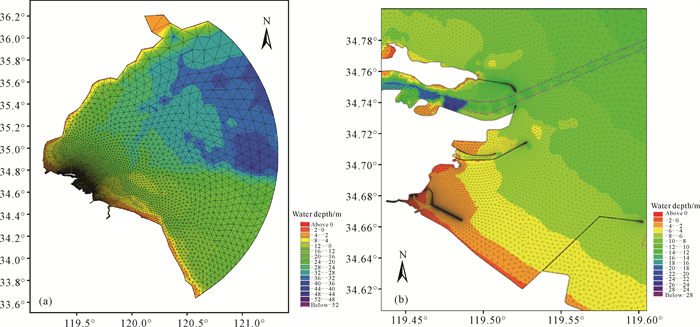
1.3.3 模型范围与网格划分研究区域潮流主要受外海潮流控制,因此采用覆盖整个连云港海域的南黄海潮流模型,以及无结构三角形网格,对研究区域进行局部加密,共形成24 363个单元格,由12 933个节点组成,最小网格分辨率为5 m (图 2)。
|
| 图 2 模型计算区域网格(a)与局部网格划分(b) Fig.2 Model calculation area grid (a) and local grid division (b) |
1.3.4 参数设置
① 糙率系数n
n由实测数据率定获得,取值0.012 5-0.040 0。
② 水流广义扩散系数E
E可用以下公式表示:
| $ E=\chi|u||L|, $ | (8) |
式中,χ为系数; |u|为特征流速,单位m/s;|L|为特征长度,单位m。E的取值为0.1-5.0 m2/s。
③ 广义物质扩散系数D
随具体环境的变化,D在一个较大的范围内变动。根据以往计算及试验资料,D可用以下公式表示:
| $ D=\phi|u||L|, $ | (9) |
式中,ϕ为系数。
④ 科氏参量f
田湾核电站位于北纬35 °附近,所以f≈8.37×10-5 rad/s。
⑤ 表面综合散热系数Ks
根据水文气象条件,采用以下公式计算Ks。
| $ K_s=(k+b) \alpha+4 \varepsilon \sigma\left(T_s+273\right)^3+\Delta K, $ | (10) |
式中,
根据研究区域附近冬季的气象、水温条件:平均水温2.6 ℃、平均气温3.0 ℃、平均气压1 025 hPa、平均相对湿度63%、平均风速5.1 m/s,计算得到Ks=24.0 W/(m2·℃)。
⑥ 表面风应力τs
τs=ρairCDvw2,ρair为空气密度,CD为系数,可采用下式确定。
| $ C_{\mathrm{D}}=\left\{\begin{array}{cl} 1.25 \times 10^{-3} / v_{\mathrm{w}}^{1 / 5} & v_{\mathrm{w}} \leqslant 1 \mathrm{~m} / \mathrm{s} \\ 0.50 \times 10^{-3} v_{\mathrm{w}}^{1 / 2} & 1<v_{\mathrm{w}} \leqslant 15 \mathrm{~m} / \mathrm{s} \\ 2.60 \times 10^{-3} & v_w>15 \mathrm{~m} / \mathrm{s} \end{array}\right.。$ | (11) |
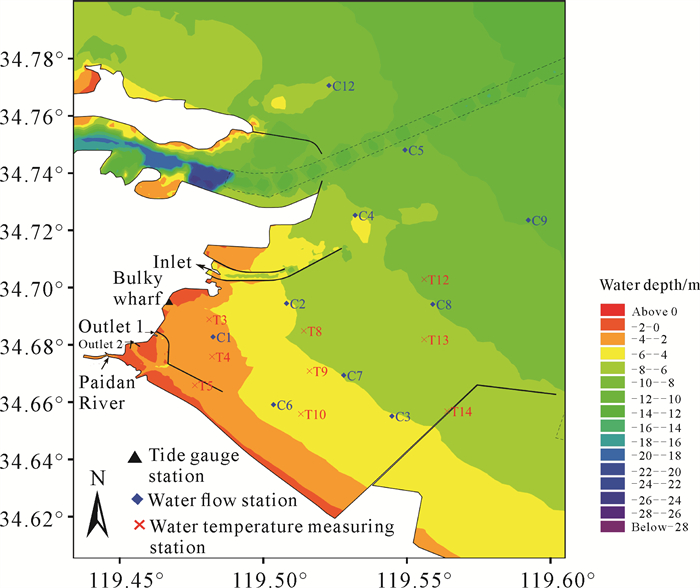
本研究收集了2021年1月的水文和2月的水温实测资料,利用大件码头实测潮位资料进行潮位验证,利用潮站C6和C7水流实测资料进行流速和流向验证,利用测站T3和T13水温实测资料进行水温验证,水文潮站和水温测站具体位置如图 3所示,验证图见图 4。其中潮位平均误差为0.04 m,各潮站流
|
| 图 3 水文潮站和水温测站位置示意图 Fig.3 Hydrological station location and water temperature station location diagram |
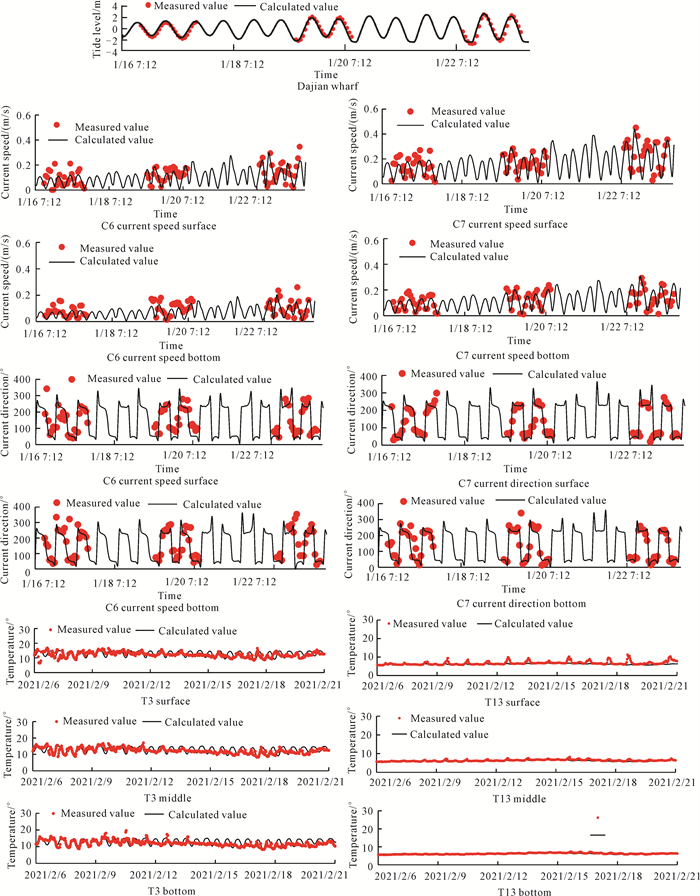
|
| 图 4 潮位、流速、流向和水温验证 Fig.4 Verification of tide level, flow velocity, flow direction and water temperature |
速平均误差为0.03 m/s;测站T13的整体水温平均误差为0.46 ℃。由于测站T3位于浅滩水域,异常海况(波况和海冰等)和气象(降水、风况、空气湿度和云量等)条件对表层水温影响较大,而对底层水温的影响较小,加之涨、落潮过程中的干、湿循环使得温度计水温监测存在一定误差,导致测站T3平均误差相对较大。验证结果表明,模拟值与实测值大体一致,能够较好地反映研究区域的潮流和水温状况,说明潮流温度数学模型可用于模拟研究区域的潮流和水温变化规律。
2 结果与分析 2.1 水温平面分布规律2021年冬季(2月)9个水温测站(T3-T5、T8-T10、T12-T14)实测水温平均值如表 1所示,水温平均值呈现出由岸向海逐渐降低的趋势。
| 水温测站 Water temperature measuring station |
平均水温/℃ Average water temperature/℃ |
| T3 | 12.97 |
| T4 | 12.61 |
| T5 | 12.92 |
| T8 | 8.95 |
| T9 | 8.58 |
| T10 | 9.06 |
| T12 | 6.12 |
| T13 | 6.47 |
| T14 | 6.84 |
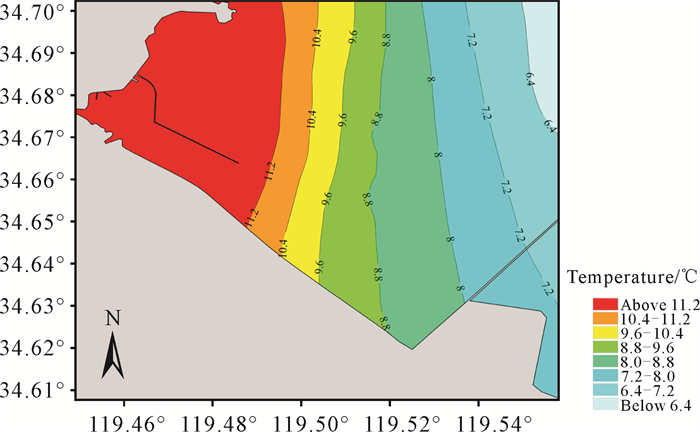
田湾核电站附近海域冬季平均水温分布特征如图 5所示,由于排水口附近分布有浅滩且水深较浅,附近海域整体升温较快,排水口以东约3 km的近岸海域温度较高,水温整体在11.2 ℃以上。由11.2 ℃等水温线向东,研究海域的水温平面呈南北向带状分布,由西向东的平面温度梯度为0.9 ℃/km。
|
| 图 5 田湾核电站附近海域冬季平均水温分布特征 Fig.5 Distribution characteristics of average water temperature in the sea area near Tianwan nuclear power station in winter |
2.2 水温立面分布规律
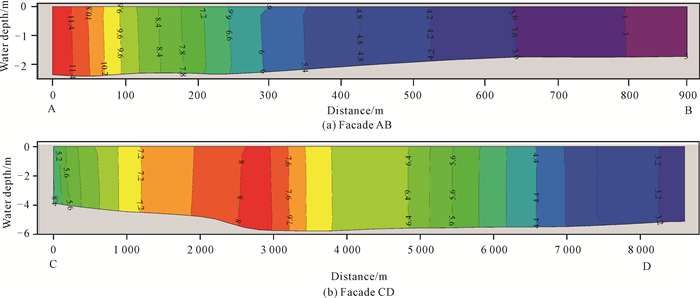
基于经校验的三维温排水数学模型,对研究区域的水温立面分布规律进行分析。立面AB和CD的水温分布如图 6所示。立面AB水深为1.5-2.4 m,距A侧约300 m处,由于热水的浮力效应,高温水舌向B侧延伸。整体来说,由于立面AB水深较浅且水流流速较大,强烈的垂向掺混作用导致温度沿垂线分布均匀,梯度较小,A侧水深、单宽流量、水平温度梯度均大于B侧;立面AB表层的水平温度梯度为9.9 ℃/km,底层为9.6 ℃/km,略小于表层[图 6(a)]。
|
| 图 6 立面AB和CD水温分布图(温度单位为℃) Fig.6 Facade AB and CD water temperature distribution (temperature unit is ℃) |
立面CD水深为4.0-5.5 m,C侧水深小于D侧;排淡河0 ℃温升河水沿流路主要在D侧排放入海,温排水受排淡河温升河水挤压主要在C侧排放入海,4 ℃温升范围大致位于距C点1 200-4 700 m处;经过一个全潮过程,立面CD范围的海水水温垂向混合较为充分,温度梯度较小;从热水团中央向C侧的水平温度梯度为1.24 ℃/km,向D侧为0.9 ℃/km,同样具有表层水平温度梯度略大于底层的特点[图 6(b)]。
此外,研究区域小潮潮段平均垂向温度梯度大于大潮,表明小潮时垂向掺混强度弱,表、底层温差大,水温分层较明显;垂向温度梯度最大为0.18 ℃/m,且随着水深的增加呈减小趋势。
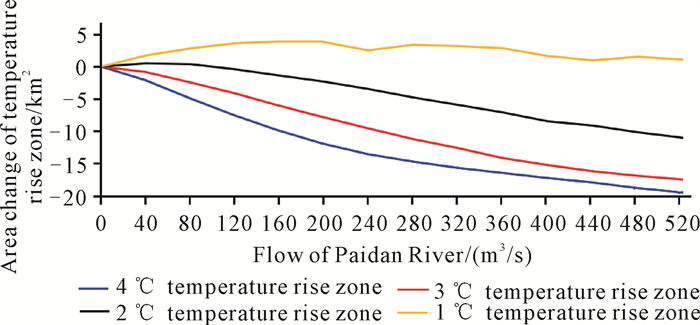
2.3 河流排涝对温排水扩散面积的影响分析研究区域附近冬季温升为10 ℃,模拟15 d的温排水扩散,以排淡河0 m3/s流量为基准,分别统计各流量工况下4、3、2、1 ℃温升面积的变化,结果如表 2所示。由于排淡河下泄水流的温升为0 ℃,排淡河排水会导致研究区域的4、3、2、1 ℃温升面积出现不同程度的变化(图 7)。温升面积缩小率定义为温升区面积变化与流量变化的比值,即为图 7温升区面积变化曲线的斜率。由表 2和图 7可知,随着排淡河排水流量的增加,与排淡河排水流量0 m3/s工况的各温升面积相比,4℃温升面积呈缩减趋势,最大缩小19.36 km2(523.6 m3/s工况),单位流量的增加造成4 ℃温升面积缩小率由0.05 (km2·s)/m3逐渐减小至0.02 (km2·s)/m3;3 ℃温升面积呈缩减趋势,最大缩小17.37 km2(523.6 m3/s工况),单位流量的增加造成3 ℃温升面积缩小率由0.05 (km2·s)/m3逐渐减小至0.03 (km2·s)/m3;2 ℃温升面积先增大再缩减,最大增大0.50 km2(40 m3/s工况),最大缩小10.94 km2(523.6 m3/s工况),单位流量的增加造成2 ℃温升面积缩小率为0.03 (km2·s)/m3;1 ℃温升面积呈波动增大趋势,最大增加3.88 km2(160 m3/s工况)。
| 流量/(m3/s) Flow/(m3/s) |
温升区面积/km2 Area of temperature rise zone/km2 |
|||
| 4 ℃ | 3 ℃ | 2 ℃ | 1 ℃ | |
| 0 | 0.00 | 0.00 | 0.00 | 0.00 |
| 40 | -2.11 | -0.84 | 0.50 | 1.71 |
| 80 | -4.88 | -2.42 | 0.38 | 2.79 |
| 120 | -7.49 | -4.09 | -0.40 | 3.59 |
| 160 | -9.79 | -5.96 | -1.34 | 3.88 |
| 200 | -11.85 | -7.76 | -2.29 | 3.81 |
| 240 | -13.46 | -9.48 | -3.43 | 2.50 |
| 280 | -14.61 | -11.13 | -4.73 | 3.34 |
| 320 | -15.57 | -12.52 | -5.88 | 3.15 |
| 360 | -16.36 | -14.07 | -7.04 | 2.83 |
| 400 | -17.14 | -15.14 | -8.41 | 1.64 |
| 440 | -17.82 | -16.09 | -9.06 | 0.95 |
| 480 | -18.69 | -16.80 | -10.10 | 1.52 |
| 523.6 | -19.36 | -17.37 | -10.94 | 1.08 |
|
| 图 7 排淡河不同流量工况下田湾核电站温排水各温升区面积变化 Fig.7 Changes in the area of each temperature rise zone of Tianwan Nuclear Power Station under different flow conditions of Paidan River |
2.4 河流排涝对温排水扩散范围的影响分析
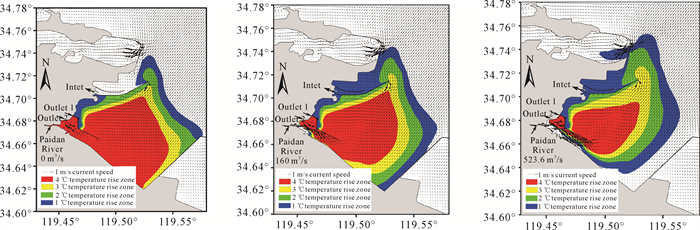
排淡河不同流量工况下田湾核电站温排水各温升区范围如图 8所示。由温升包络图可知,从排水口排出的高温水主要在射流作用下沿着排水导流堤向东扩散,流出导流堤之后在徐圩港区防波堤的束缚下向东北方向扩散,至防波堤外后受潮流的顶托作用转向北扩散,且沿流路的扩散距离大于横向扩散距离。此外,研究区域内的温排水扩散与其载体——潮流均呈现出东北-西南向往复流的特性[21]。当温排水进入外海,热水浮力较大,其产生的羽流效应及冷热水的热传递起主导作用,导致冷热水在交汇处形成流向与潮流方向一致的趋势。
|
| 图 8 排淡河不同流量工况下田湾核电站温排水各温升区范围 Fig.8 Range of each temperature rise zone of thermal discharge of Tianwan Nuclear Power Station under different flow conditions of Paidanhe River |
随着排淡河排水流量增大(0-160 m3/s),在温排水初始混合过程阶段4、3、2、1 ℃温升区范围均向北移动;当排淡河排水流量继续增大(160-523.6 m3/s),4 ℃温升区范围向南收缩,3、2、1 ℃温升区范围继续北移。水流受导流堤、防波堤等工程建筑物的制约在局部出现较大梯度,使得1 ℃温升区在局部出现转折。
对比排淡河排水流量0、160、523.6 m3/s工况下的流场可知,随着排水流量增大,排淡河入海河道处的低温升区范围越大。在排水导流堤与海岸的约束下,0 ℃温升的入海河水与田湾核电站温排水均沿东南偏东方向排海。与排淡河排水流量0 m3/s的各温升区范围相比,随着排淡河流量增大,4 ℃温升区先向北逐渐扩展,最大向北扩展约500 m(160 m3/s),超出了排淡河排水流量0 m3/s时的4 ℃温升区范围。当排淡河排水流量大于160 m3/s后,4 ℃温升区再向南逐渐收缩约600 m;3 ℃温升区向北扩展最大距离为1.6 km;2、1 ℃温升区向北扩展最大距离均为1.7 km。
根据菲克定律,当水流宏观流速较小时,分子热扩散主要由温度梯度驱动。而依据湍流扩散理论,当水流宏观流速较大时,热量传递主要通过紊动和对流扩散作用进行,热量传递效率与流速成正比。由于地形的束缚,随着排淡河流量的增大,研究区域局地平均流速均有所增大,热量传递效率随之增大。因此,随着排淡河排水流量的增大(160-523.6 m3/s),温排水扩散范围逐渐向西收缩。
3 结论本研究建立了田湾核电站温排水三维数学模型,在充分校验的基础上,分析了排淡河不同排水流量下温排水扩散范围及其规律,得出以下结论。
① 基于水温实测资料及经校验的温排水三维数学模型,分析了研究区域冬季的平面和立面分布特征。平面上,排水口以东约3 km水域的水温在11.2 ℃以上,由此向东的水温呈南北向带状分布,温度梯度为0.9 ℃/km;立面上,研究区域水深浅,垂向掺混作用强烈,温度梯度最大为0.18 ℃/m,底层的水平温度梯度略小于表层。
② 在考虑排淡河不同流量的情况下,随着排水流量的增加,4、3 ℃温升面积呈缩减趋势,单位流量的增加造成4、3 ℃温升面积缩小率从0.05 (km2·s)/m3分别减小至0.02、0.03 (km2·s)/m3,最大缩小面积分别为19.36、17.37 km2(523.6 m3/s工况);2 ℃温升面积先增大再缩减,单位流量的增加造成温升面积缩小,缩小率为0.03 (km2·s)/m3;1 ℃温升面积呈波动增大趋势,最大增加3.88 km2(160 m3/s工况)。
③ 从空间分布上看,田湾核电站温排水近区的河流排涝显著影响了温排水的扩散范围。随着排水流量的增加,4、3、2、1 ℃温升区均向北扩展,当流量增大至160-523.6 m3/s时,3、2、1 ℃温升区范围继续北移;而随着排淡河排水流量的增大,热量传递效率同步增加,当排淡河排水流量大于160 m3/s后,4 ℃温升区转而向南收缩。
为进一步刻画研究区域内的水温分布特征及温排水的扩散规律,还需收集更多海况和气象资料。随着排淡河排水流量的增加,4 ℃温升区范围先向北扩展再向南收缩的现象与3、2、1 ℃温升区变化特征不同的原因也有待进一步探讨。



